Complete Solutions to Single correct Answer Type of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| CENGAGE PHYSICS | Single correct Answer Type |
| Number Of Questions | 53 |
| Academic Year | 2023-24 |
In an interference arrangement similar to Young's double-slit experiment, the slits S_1 and S_2 are illuminated with coherent microwave sources, each of frequency 10^6 Hz. The sources are synchronized to have zero phase difference. The slits are separated by a distance d=150.0 m. The intensity I (theta) is measured as a function of theta, where theta is defined as shown. If I_0 is the maximum intensity, then I (theta) for 0lethetale90degree is given by

View SolutionA thin slice is cut out of a glass cylinder along a plane parallel to its axis. The slice is placed on a flat glass plate as shown in Figure. The observed interference fringes from this combination shall be
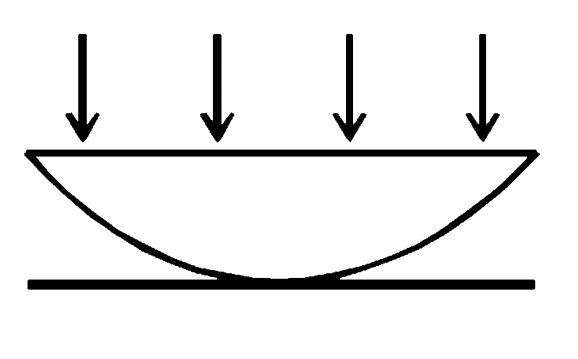
View SolutionIn a double slit experiment instead of taking slits of equal widths, one slit is made twice as wide as the other. Then, in the interference pattern
View SolutionTwo beams of ligth having intensities I and 4I interface to produce a fringe pattern on a screen. The phase difference between the beams is `(pi)/(2)` at point A and `pi` at point B. Then the difference between the resultant intensities at A and B is
View SolutionIn a Young's double slit experiment, 12 fringes are observed to be formed in a certain segment of the screen when light of wavelength 600nm is used. If the wavelength of light is changed to 400nm, number of fringes observed in the same segment of the screen is given by
View SolutionIn the ideal double-slit experiment, when a glass-plate(refractive index 1.5) of thickness t is introduced in the path of one of the interfering beams (wave-length `lamda`), the intensity at the position where the central maximum occurred previously remains unchanged. The minimum thickness of the glass-plate is
View SolutionIn the adjacent diagram, CP represents a wavefront and AO & BP, the corresponding two rays. Find the condition on `theta` for constructive interference at P between the ray BP and reflected ray OP.
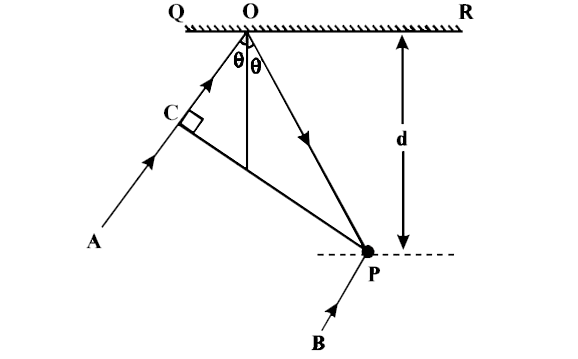
View SolutionMonochromatic light of walelength 400nm and 560nm are incident simultaneously and normally on double slits apparatus whose slit sepation is 0.1 mm and screen distance is 1m. Distance between areas of total darkness will be
View SolutionIn Young's double slit experiment intensity at a point is `((1)/(4))` of the maximum intersity. Angular position of this point is
View SolutionA light ray travelling in glass medium is incident of glass- air interface at an angle of incidence `theta`. The reflected `(R )` and transmitted (T) intensities, both as function of `theta`, are plotted The correct sketch is
View SolutionYoung's double slit experiment is carried out by using green, red and blue light, one color at a time. The fringe width recorded are `b_(G)`,`b_(R)` and `b_(B)` respectively. Then,
View SolutionIn the Young's double slit experiment using a monochromatic light of wavelength `lamda`, the path difference (in terms of an integer n) corresponding to any point having half the peak
View SolutionThe ratio of intensities of two waves is `9 : 1` When they superimpose, the ratio of maximum to minimum intensity will become :-
View SolutionFor different independent waves are represented by
a) `Y_(1)=a_(1)sin omega_(1)t` , b) `Y_(2)=a_(2) sin omega_(2)t`
c) `Y_(3)=a_(3) sin omega_(3)t` , d) `Y_(4)=a_(4) sin(omega_(4)t+(pi)/(3))`
The sustained interference is possible due to
View SolutionA ray of light intensity I is incident on a parallel glass-slab at a point `A` as shown in figure. It undergoes partial reflection and refraction. At each reflection `25%` of incident energy is reflected. The rays `AB` and `A^(')B^(')` undergo interference. The ratio `I_(max)//I_(min)` is

View SolutionIn the adjacent diagram, CP represents a wavefront and AO & BP, the corresponding two rays. Find the condition on `theta` for constructive interference at P between the ray BP and reflected ray OP.

View SolutionFigure here shown P and Q as two equally intense coherent sources emitting radiations of wavelength 20 m. The separation PQ is 5.0 m and phase of Q is ahead of the phase of P by `90^(@)`. A,B and C are three distant points of observation equidistant from the mid-point of PQ. The intensity of radiations at A,B and C will bear the ratio
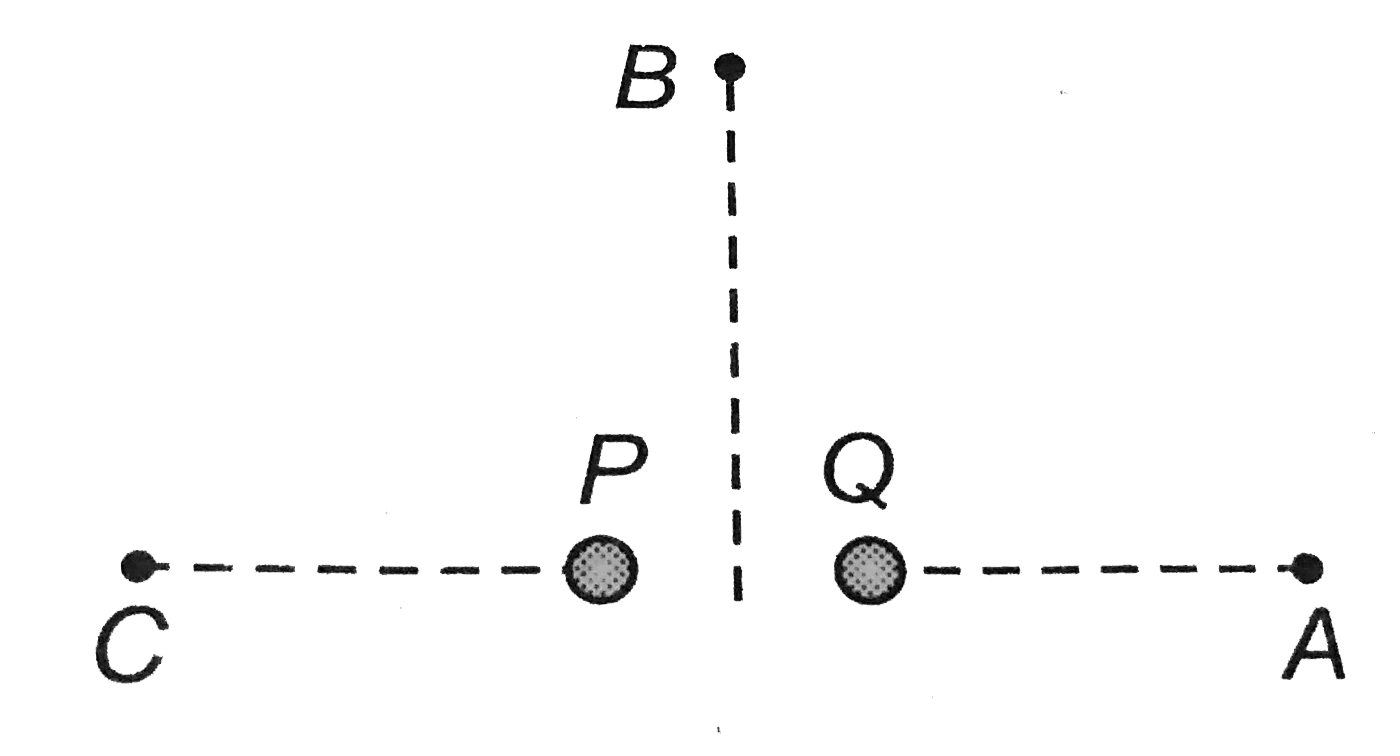
View SolutionTwo point sources X and Y emit waves of same frequency and speed but Y lags in phase behind X by `2pi//radian`. If there is a maximum in direction D the distance XO using n as an integer is given by
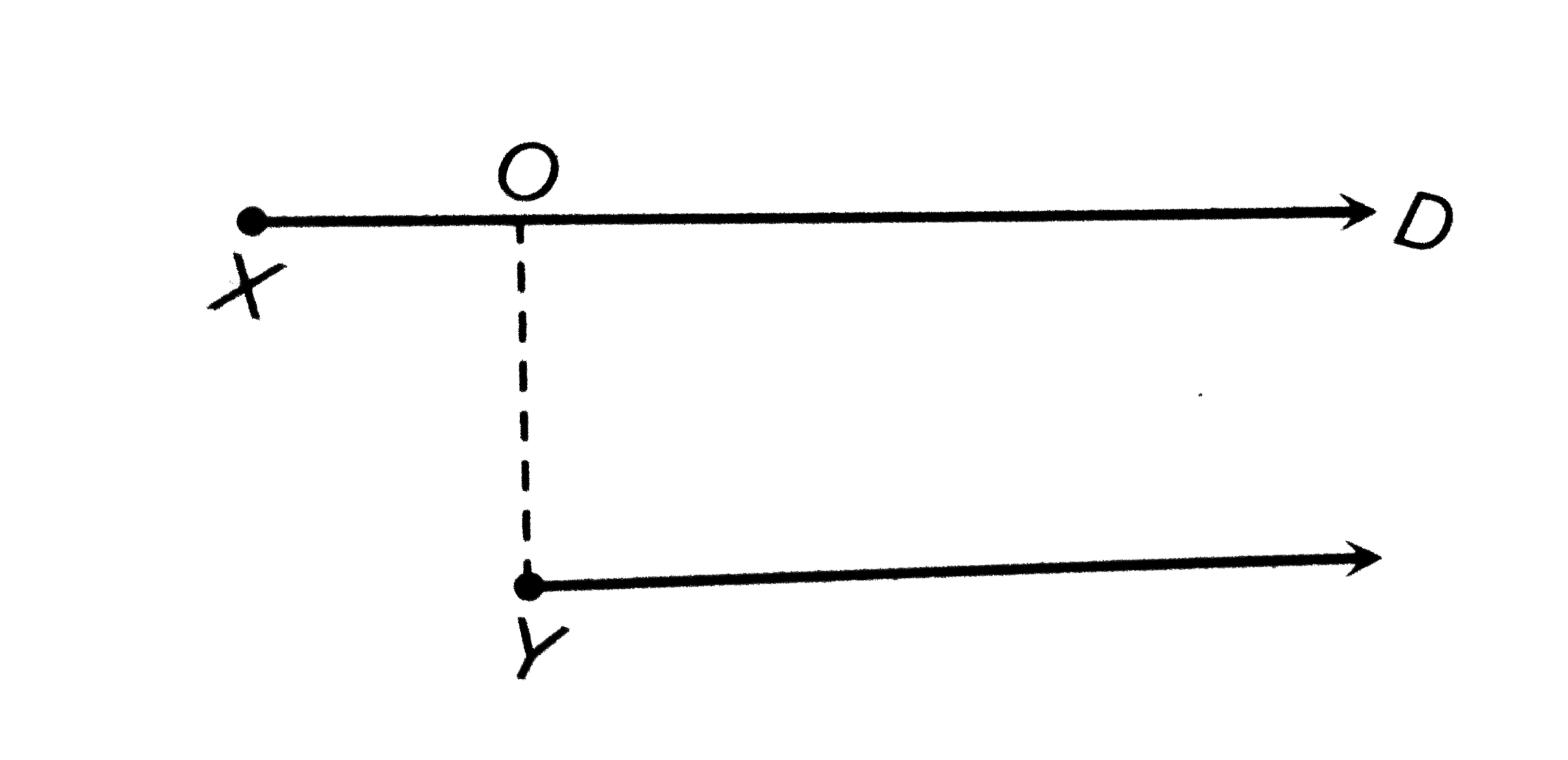
View SolutionFollowing figures shows sources `S_1` and `S_2` that emits light of wavelength `lambda` in all directions. The sources are exactly in phase and are separated by a distance equal to `1.5lambda`. If we start at the indicated start point and travel along path 1 and 2, the interference produce a maxima all along

View SolutionTwo coherent sources separated by distance d are radiating in phase having wavelength `lambda`. A detector moves in a big circle around the two sources in the plane of the two sources. The angular position of `n=4` interference maxima is given as

View SolutionTwo coherent sources `S_1` and `S_2` area separated by a distance four times the wavelength `lambda` of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
View SolutionThree waves of equal frequency having amplitudes `10mum`, `4mum`, `7mum` arrive at a given point with successive phase difference of `pi//2`, the amplitude of the resulting wave in `mum` is given by
View SolutionTwo identical radiators have a separation of `d=lambda//4` where `lambda` is the wavelength of the waves emitted by either source. The initial phase difference between the sources is `lambda//4`. Then the intensity on the screen at a distant point situated at an angle `theta=30^@` from the radiators is (here `I_0` is intensity at that point due to one radiator alone)
View SolutionIn Young's double slit experiment, if the two slits are illuminated with separate sources, no interference pattern is observed because
View SolutionIn Young's double slit experiment if monochromatic light is replaced by white light
View SolutionIn the set up shown in figure, the two slits `S_1` and `S_2` are not equidistant from the slit S. The central fringe at O is then
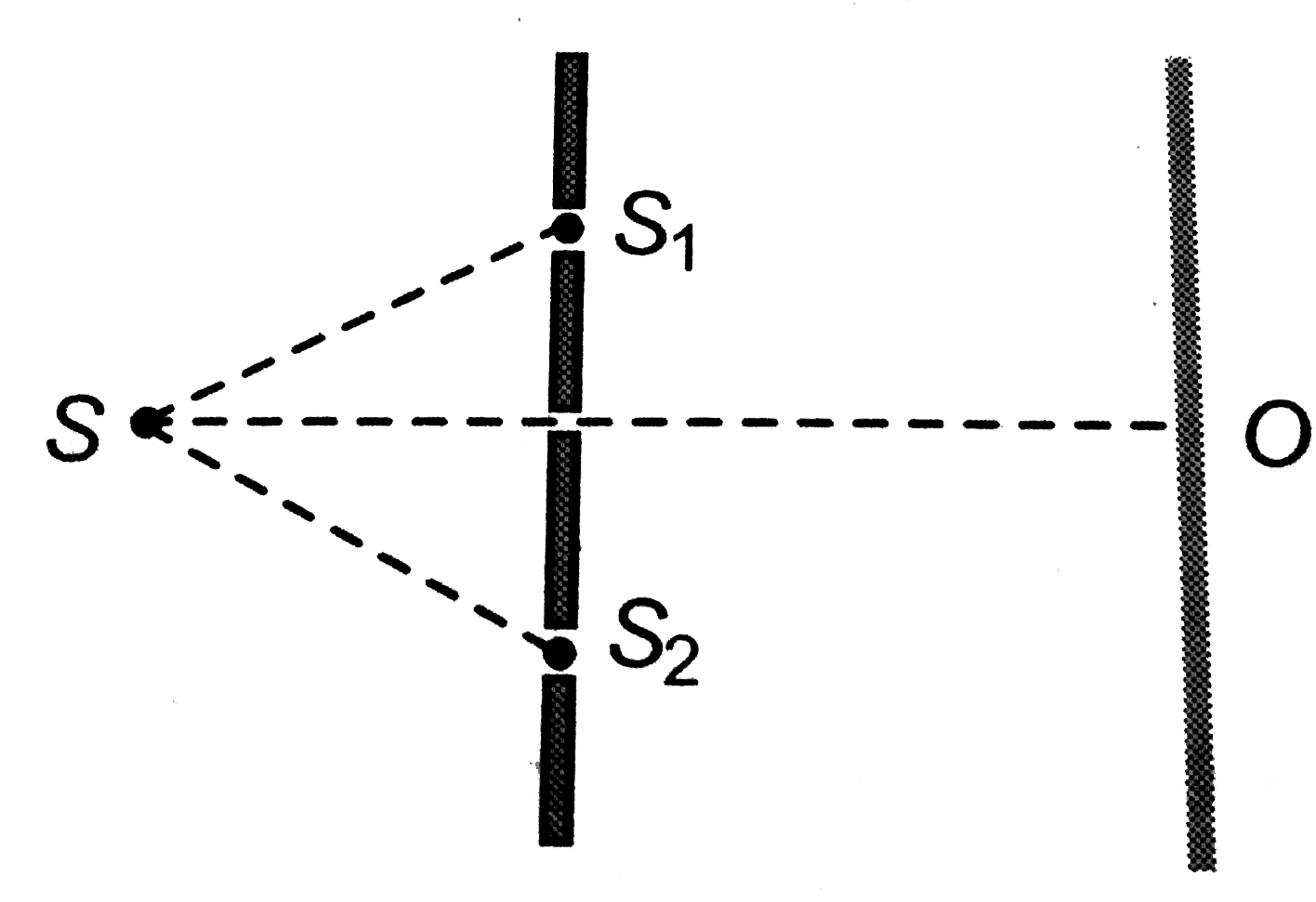
View SolutionThe maximum intensity of fringes in Young's experiment is I. If one of the slit is closed, then the intensity at that place becomes `I_o`. Which of the following relation is true?
View SolutionIn Young's double slit experiment, if the slit widths are in the ratio `1:9`, then the ratio of the intensity at minima to that at maxima will be
View SolutionIn Young's double slit experiment, the intensity on the screen at a point where path difference is `lambda` is K. What will be the intensity at the point where path difference is `lambda//4`?
View SolutionThe maximum intensity in young's double-slit experiment is `I_(0)`. Distance between the slit is `d = 5 lambda`, where `lambda` is the wavelength of monochromatic light used in the experiment. What will be the intensity of light in front of one of the slits on a screen at a distance `D = 10 d`?
View SolutionTwo coherent sources of equal intensity produce maximum intensity of `100` units at a point. If the intensity of one of the sources is reduced by 36% reducing its width, then the intensity of light at the same point will be
View SolutionIn a Young's double slit experiment, `I_0` is the intensity at the central maximum and `beta` is the fringe width. The intensity at a point P distant x from the centre will be
View SolutionThe path difference between two interfering waves of equal intensities at a point on the screen is `lambda//4`. The ratio of intensity at this point and that at the central fringe will be
View SolutionIn Young's double-slit experiment , we get 60 fringes in the field of view if we use light of wavelength `4000 Å`. The number of fringes we will get in the same field of view if we use light of wavelength `6000 Å` is
View SolutionThe figure shows a double slit experiment with P and Q as the slits. The path lengths PX and QX are `nlambda` and `(n+2)lambda` respectively, where n is a whole number and `lambda` is the wavelength. Taking the central fringe as zero, what is formed at X?
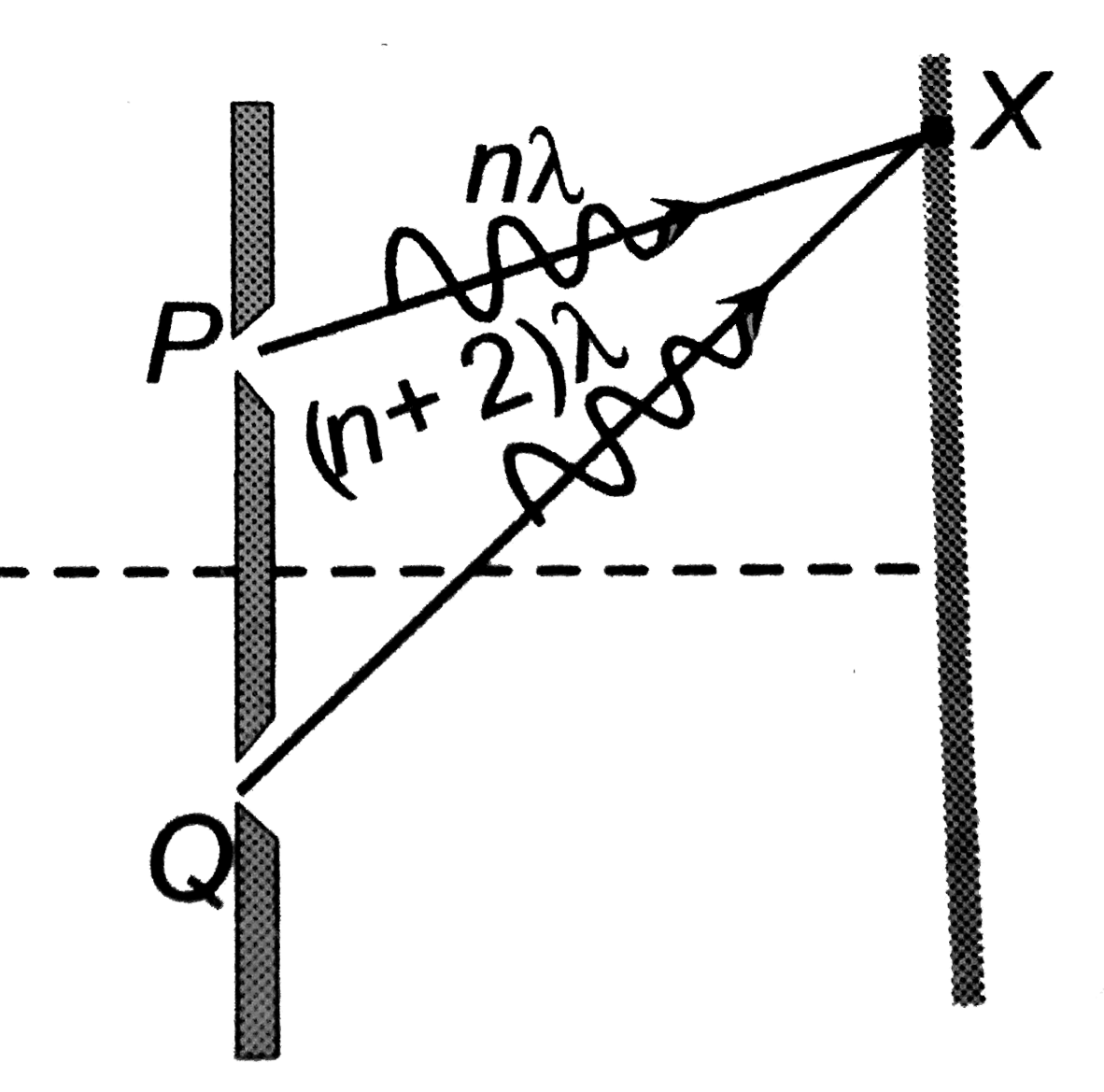
View SolutionIn a two slit experiment with monochromatic light fringes are obtained on a screen placed at some distance from the sits. If the screen is moved by m `5 xx 10^(-2)m` towards the slits, the change in fringe width is m `3 xx 10^(-5)m` . If separation between the slits is `10^(-3)m` , the wavelength of light used is
View SolutionIn Young's double slit experiment how many maximas can be obtained on a screen (including the central maximum) on both sides of the central fringe if `lambda=2000Å` and `d=7000Å`
View SolutionIn a Young's double slit experimental arrangement shown here, if a mica sheet of thickness t and refractive indec `mu` is placed in front of the slit `S_1`, then the path difference `(S_1P-S_2P)` is

View SolutionIn Young's experiment, monochromatic light is used to illuminate the two slits A and B. Interference fringes are observed on a screen placed in front of the slits. Now if a thin glass plate is placed normally in the path of the beam coming from the slit
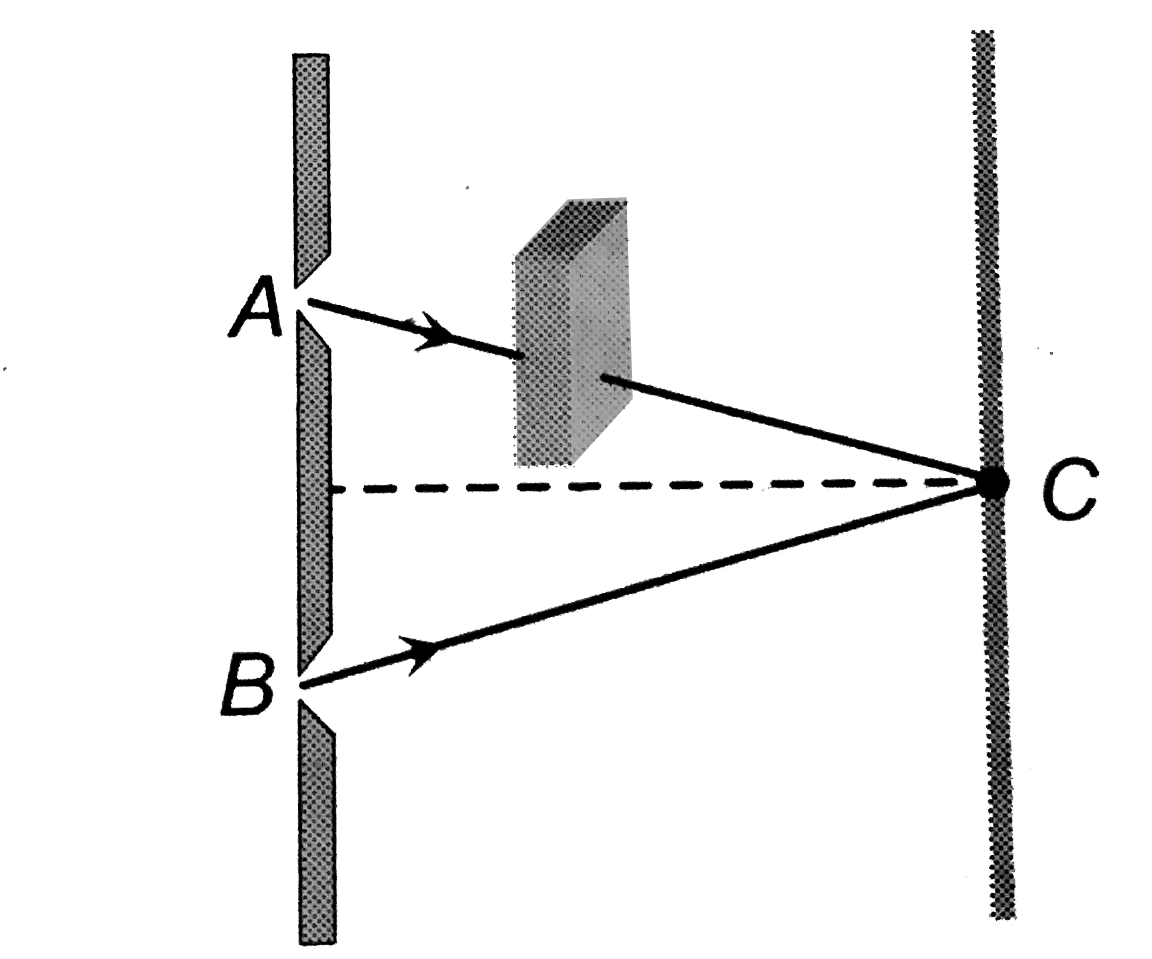
View SolutionA thin mica sheet of thickness `2xx10^-6m` and refractive index `(mu=1.5)` is introduced in the path of the first wave. The wavelength of the wave used is `5000Å`. The central bright maximum will shift
View SolutionWhen one of the slits of Young's experiment is covered with a transparent sheet of thickness `4.8mm`, the central fringe shifts to a position originally occupied by the 30th bright fringe. What should be the thickness of the sheet if the central fringe has to shift to the position occupied by 20th bright fringe?
View SolutionLight of wavelength `500nm` is used to form interference pattern in Young's double slit experiment. A uniform glass plate of refractive index `1.5` and thickness `0.1mm` is introduced in the path of one of the interfering beams. The number of fringes which will shift the cross wire due to this is
View SolutionA flake of glass (refractive index 1.5) is placed over one of the openings of a double slit apparatus. The interference pattern displaces itself through seven succesive maxima towards the side where the flake is placed. If wavelength of the diffracted light is `lambda=600nm`, then the thickness of
View SolutionIn Young's double slit experiment, the fringes are displaced index 1.5 is introduced in the path of one of the beams. When this plate in replaced by another plate of the same thickness, the shift of fringes is `(3//2)x`. The refractive index of the second plate is
View SolutionIn a double-slit experiment, fringes are produced using light of wavelength `4800A^(@)`. One slit is covered by a thin plate of glass of refractive index 1.4 and the other slit by another plate of glass of double thickness and of refractive index 1.7. On doing so, the central bright fringe shifts to a position originally occupied by the fifth bright fringe from the centre. find the thickness of the glass plates.
View SolutionThe Young's double slit experiment is performed with blue light and green light of wavelength `4360 Å` and `5460 Å` respectively. If y is the distance of `4th` maxima from the central one, then
View SolutionTwo ideal slits `S_(1)` and `S_(2)` are at a distance `d` apart, and illuninated by light of wavelength `lambda` passing through an ideal source slit `S` placed on the line through `S_(2)` as shown. The distance between the planes of slits and the source slit is `D.A` screen is held at a distance `D` from the plane of the slits. The minimum value of `d` for which there is darkness at `O` is `(dlt lt D)`
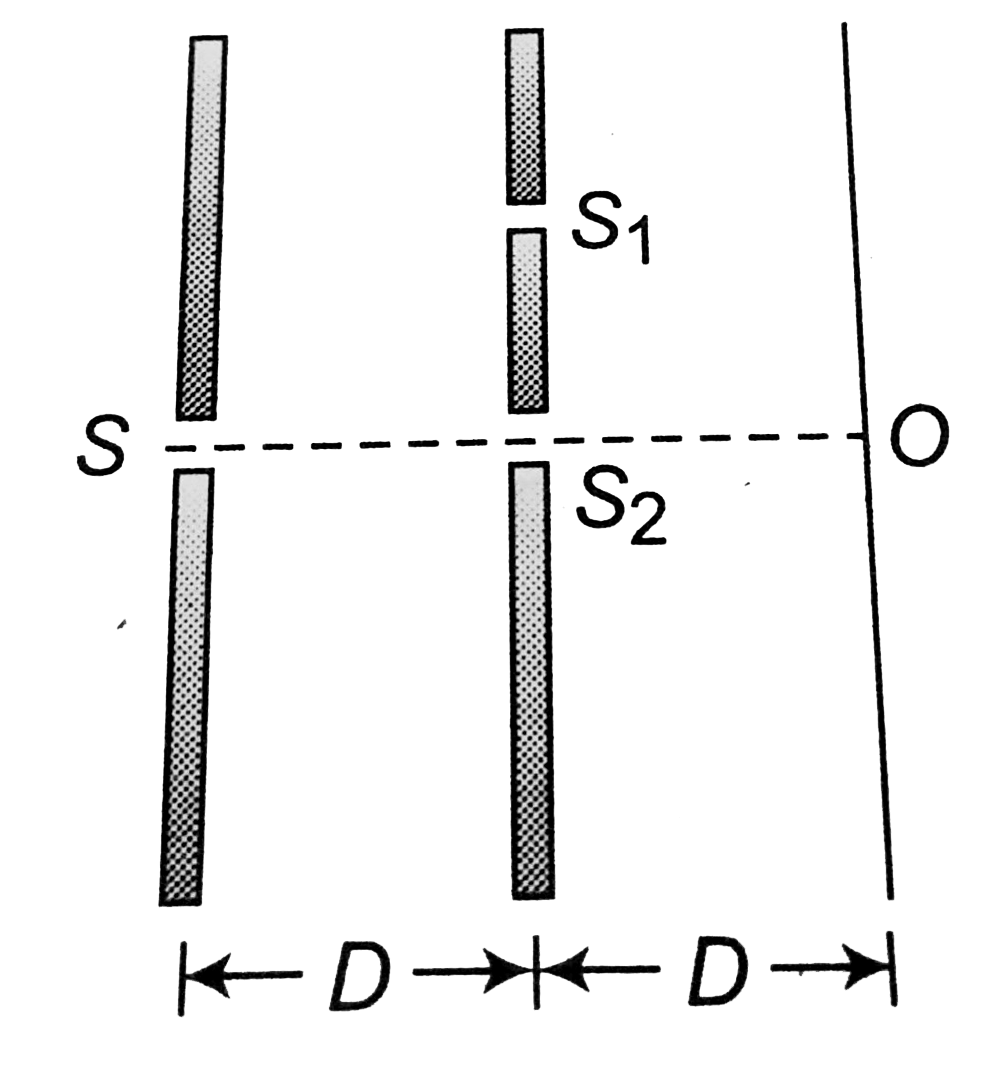
View SolutionA beam with wavelength `lambda` falls on a stack of partially reflecting planes with separation `d`. The angle `theta` that the beam should make with planes so that the beams reflected from successive planes may interfere constructively is (where n=1, 2, ...)
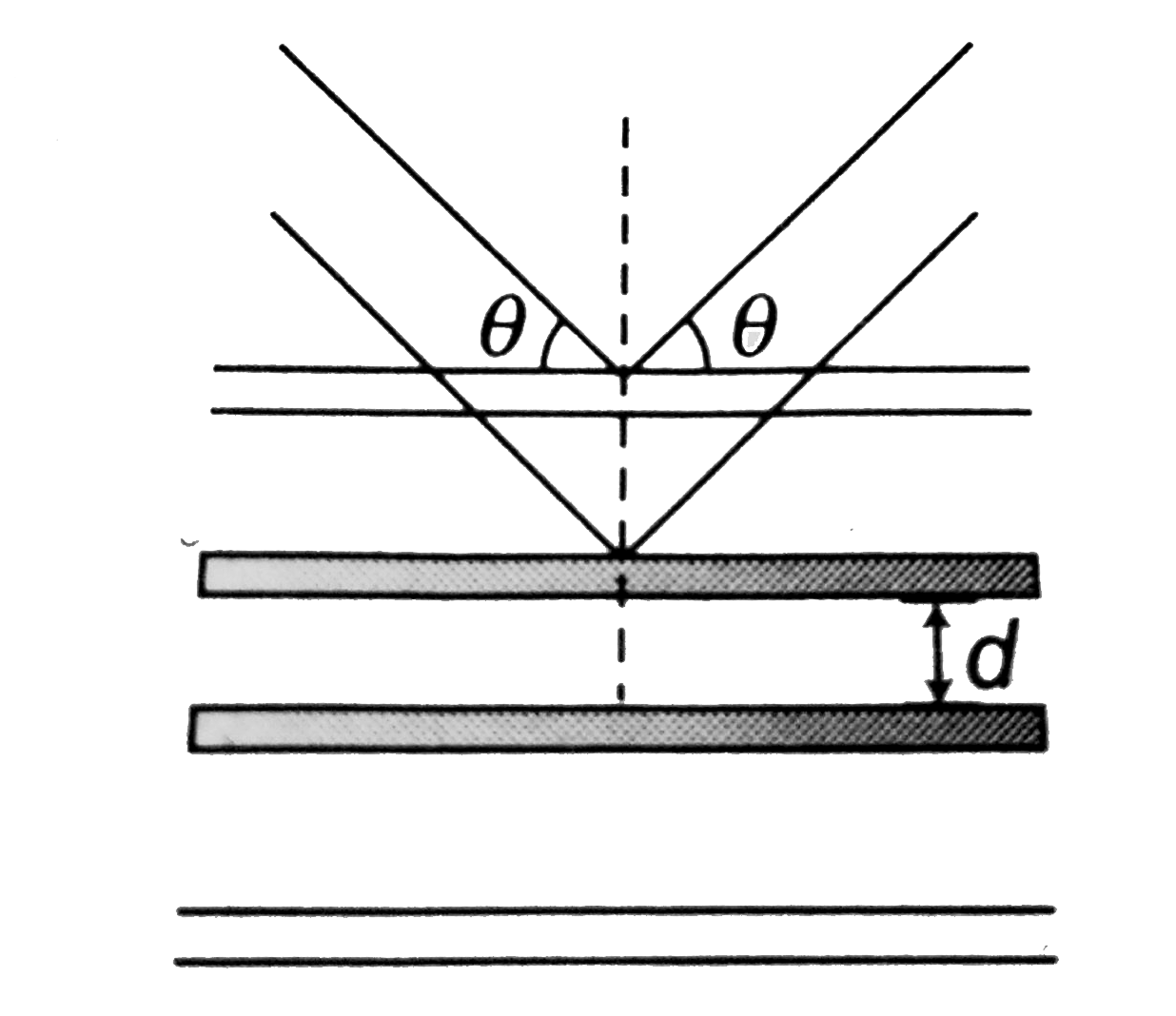
View SolutionWhite light may be considered to be mixture of waves of `lambda` ranging between `3900 Å` and `7800 Å`. An oil film of thickness `10,000 Å` is examined normally by the reflected light. If `mu=1.4`, then the film appears bright for
View SolutionA light of wavelength `5890Å` falls normally on a thin air film. The minimum thickness of the film such that the film appears dark in reflected light is
View SolutionWhat is the effect on Fresnel's biprism experiment when the use of white light is made?
View SolutionIn a biprism experiement, by using light of wavelength `5000Å`, `5mm` wide fringes are obtained on a screen `1.0m` away from the coherent sources. The separation between the two coherent sources is
View SolutionIn Fresnel's biprism `(mu=1.5)` experiment the distance between source and biprism is `0.3m` and that between biprism and screen is `0.7m` and angle of prism is `1^@`. The fringe width with light of wavelength `6000Å` will be
View Solution
Single correct Answer Type questions and complete solutions for chapter WAVE OPTICS of CENGAGE PHYSICS (HINGLISH) of Class 12