Complete Solutions to Illustration of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| CENGAGE PHYSICS | Illustration |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
Light waves from two coherent sources superimpose at a point. The waves, at this point, can be expressed as `y_(1) = a sin [10^(15) pi t]` and `y_(2)a sin [10^(15) pi t + phi]`. Find the resultant amplitude if phase difference `phi` is
(a) zero
(b) `pi//3`
(c) `pi`
Also find the frequency (Hz) of resultant wave in each case.
View SolutionIn young's experiment, the interfacing waves have amplitudes in the ratio `3:2`. Find the ratio of (a) amplitudes and (b) intensities, between the bright and dark fringers.
View SolutionTwo coherent sources emit light waves which superimpose at a point where these can be expressed as
`E_(1) = E_(0) sin(omega t + pi//4)`
`E_(2) = 2E_(0) sin(omega t - pi//4)`
Here, `E_(1) and E_(2)` are the electric field strenghts of the two waves at the given point.
If I is the intensity of wave expressed by field strenght `E_(1)`, find the resultant intensity
View SolutionDetermine the resultant of two waves given by `y_(1) = 4 sin(200 pi t) and y_(2) = 3 sin(200 pi t + pi//2)`.
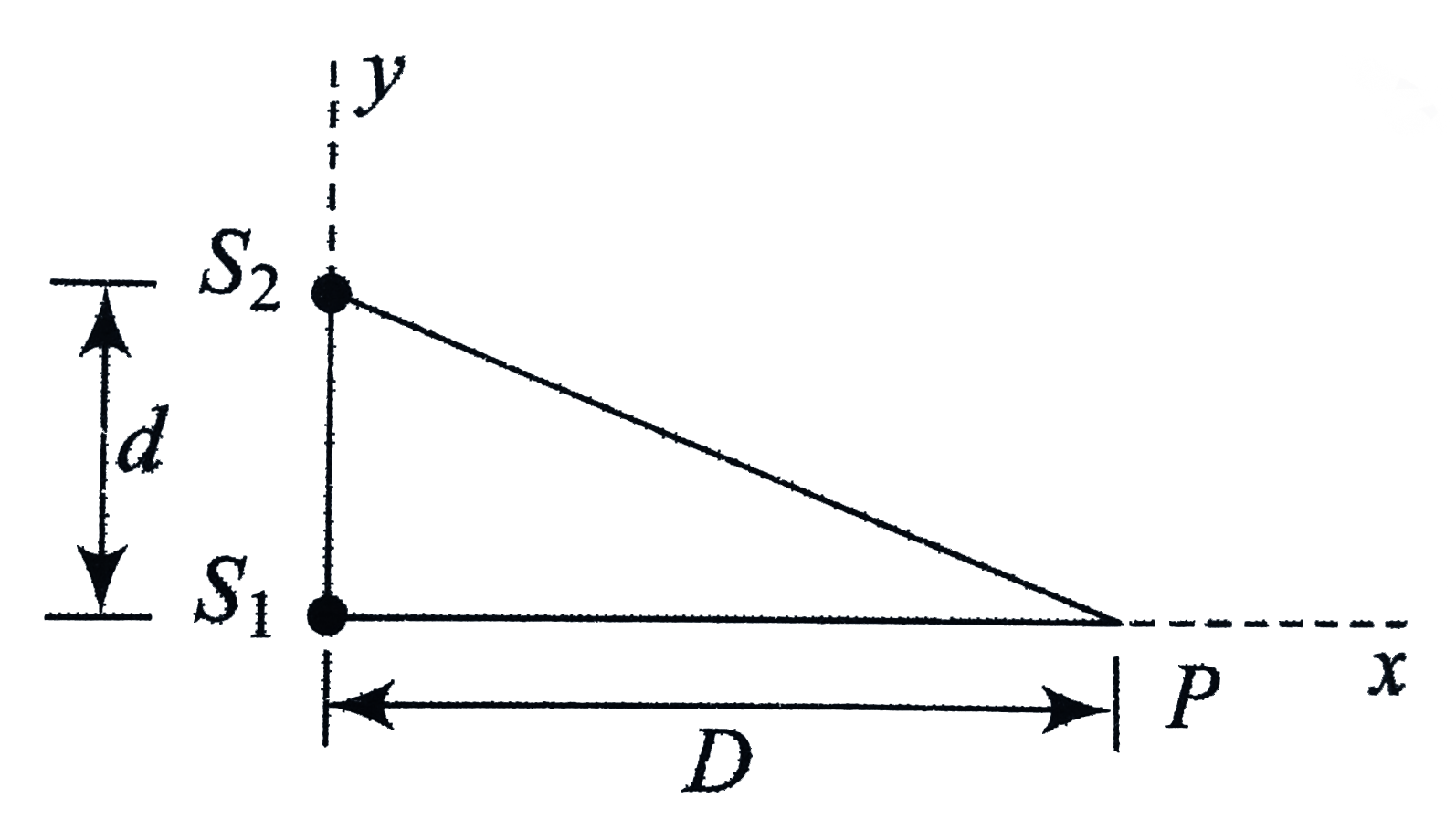
View SolutionTwo sources `S_(1)` and `S_(2)` emitting light of wavelength 600 nm placed a distance `1.0 xx 10^(-2)` cm apart.
A detector can be moved on line `S_(1) P` which is perpendicular to `S_(1) S_(2)`
(a) What would be the minimum and maximum path difference at the detector as it moves along line `S_(1) P` ?
(b) Locate the position of the farthest minima detected
 .
.
View SolutionTwo coherent point sources `S_(1)` and `S_(2)` vibrating in phase emit light of wavelength `lambda`. The separation between the sources is `2lambda`. Consider a line passing through `S_(1)` and perpendicular to line `S_(1) S_(2)`. Find the position of farthest and nearest minima.
 .
.
View SolutionTwo source are placed on x-axis at a separation `d = 3lambda`. An observer starts moving from A on a circular track of radius R `(R gt gt d)`. How many bright points and dark points will he observer?
Find the angular positions of maxima and minima.
 .
.
View SolutionTwo point sources are placed on a straight line separated by a distance `d = 3 lambda`. Both the sources are placed at a distance L from a wall which is perpendicular to the straight line. Both the sources are sending waves of equal intensity.
Find:
a. Locus of the points on the wall having equal intensity.
b. Maximum and minimum path difference observed on the wall.
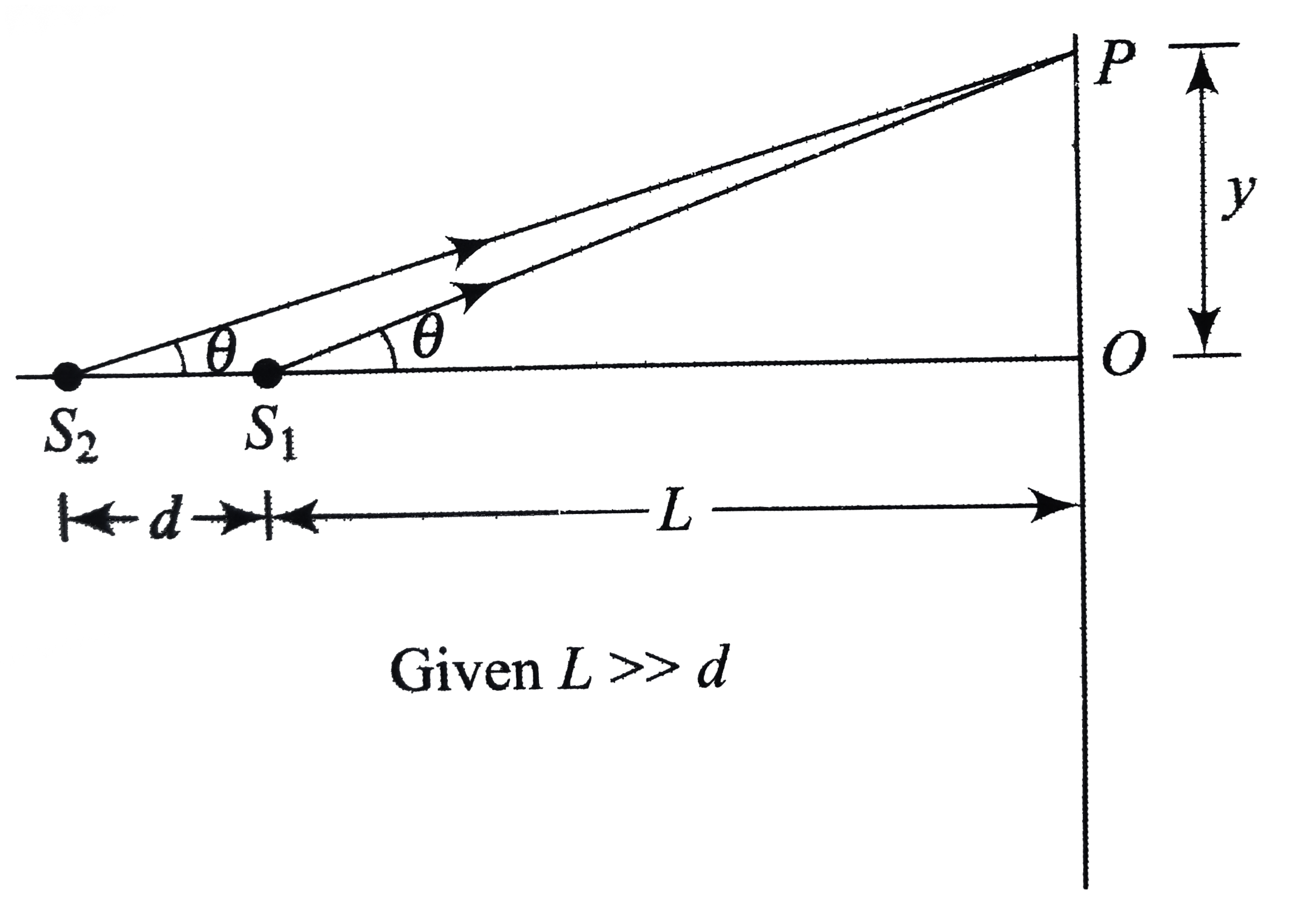
View Solution(a) In Illustration 2.20, how many dark rings will be observed on the wall? (b) What is the Path difference at point P?

View SolutionA convex lens of focal length 20 cm is cut long its diameter and the two halves are displaced by `t = 1` cm along the principal axix. A monochromatic point source of wavelength 476 nm is placed at a distance 40 cm from the first half, as shown in Fig. 2.21. Find the position of the first maximum.

View SolutionTwo parallel beams of light P and Q are incident normally on a prism and the transmitted rays are brought to focus with the help of a convergent lens as shown in Fig. 2.23. If the intensities of the upper and lower beams immediately after transmission from face AC are 4I abd I, respectively, find the resultant intensity at the focus.
View SolutionWhite light, with a uniform intensity across the visible wavelength range 430 - 690 nm, is perpendicularly incident on a wate film, of index of refraction `mu = 1.33` and thickness `d = 320`nm, that is suspended in air. At what wavelength `lambda` is the light reflected by the film brightest to an observer?
View SolutionA glass lens is coated on one side with a thin film of magnesium fluoride `(MgF_(2))`to reduce reflection from the lens surface (Fig. 2.26). The Index of refraction of `MgF_(2)` is 1.38, that of the glass is 1.50. What is the least coating thickness that eliminates (via interference) the reflections at the middle of the visible specturm `(lambda = 550nm)`? Assume that the light is approxmately perpendicular to the lens surface.
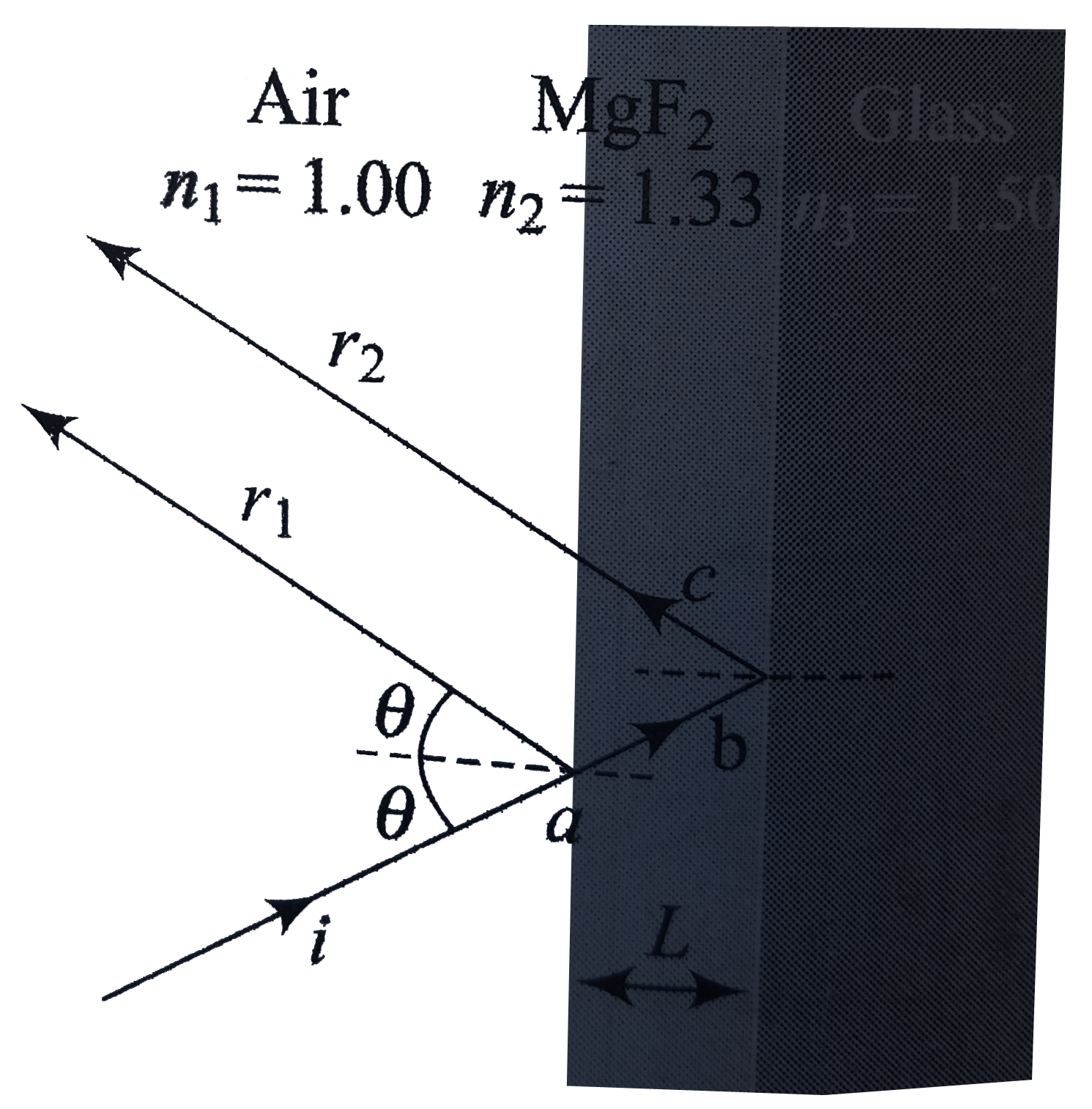
View SolutionWhite light is incident normally on a glass plate of thickness `0.50 xx 10^(-6)` and index of refraction 1.50. Which wavelengths in the visible region `(400 nm - 700 nm)` are strongly reflected by the plate?
View SolutionRed light `I(lambda = 664 nm` in vacuum) is used in Young's experiment with the slits separated by a distance from the screen given by `D = 2.75 m.` Find the distance y on the screen between the central bright fringe and the third-order bright fringe.
Reasoning: This problem can be solved by the first using Eq. (i) to determine the value of `theta` that locates the third-order bright fringe. Then, trigonometry can be used to obatin the distance y.
View SolutionIn a YDSE, `D = 1 M, d = 1 mm, and lambda = 1//2 mm.`
(a) Find the distance between the first and central maxima on the screen.
(b) Find the number of maxima and minima obtained on the screen.
View SolutionMonochromatic light of wavelength `5000 Å` is used in YDSE, with slit width, `d = 1 mm`, distance between screen and slits, `D = 1 M`. If intensites at the two slits are `I_1 = 4I_0 and I_2 = I_0`, find:
a. finge width `beta:`
b. distance of 5th minima from the central maxima on the screen,
c. intensity at `y = (1)/(3) mm,`
d. distance of the 1000th maxima, and
e. distance of the 5000th maxima.
View SolutionYoung's double slit experiment is perfor-med inside water `(mu = 43)` with light of frequency `6 xx 10^(14)` Hz. If the slits are separated by 0.2 mm and the screen kept 1 m from the slits, find the fringe width. Using the same set-up, what will the fringe width be if the experiment is performed in air?
View SolutionIn Young's experiment performed with light or wavelength 5500 Å what should be the separation between the two slits so that the highest order of maximum intensity in the interference pattern is 2 ? You may assume `D gt gt d.`
View SolutionIn Young's experiment, light of wavelength 600 nm falls on the double slits separated by 0.1 mm. What is the highest order of maximum intensity in the interference pattern obtained on a screen kept 3 m from the slits? How does the highest order change if the distance of screen from the slits is changed?
View SolutionAt a point on the screen directly in front of one of the slits, find the missing wavelengths.
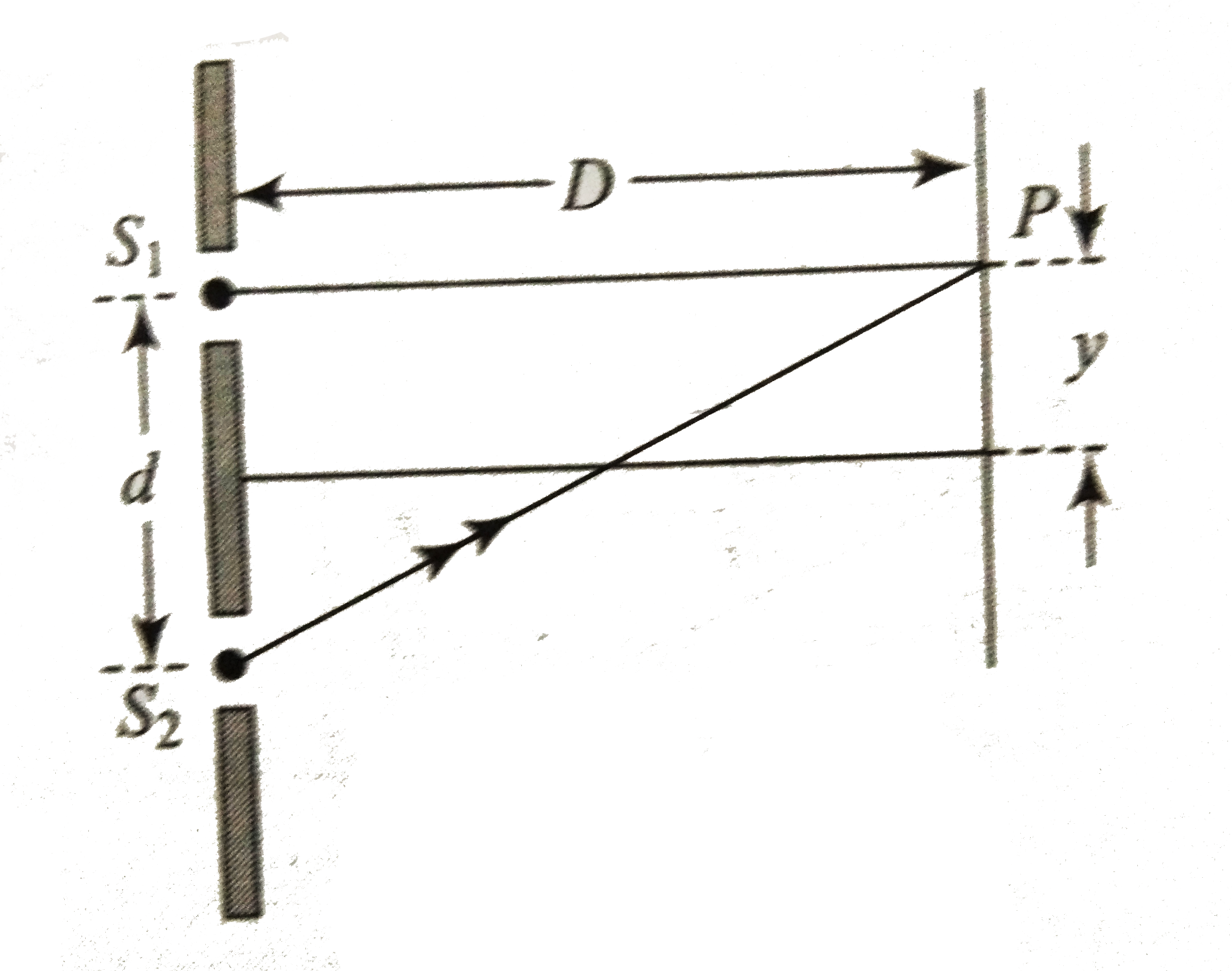
View SolutionIn Young's experiment the slits, separated by `d = 0.8 mm`, are illuminated with light of wavelength 7200 Å, Interference pattern is obtained on a screen `D = 2 m` from the slits. Find minimum distance from central maximum at which the a average intensity is 50% if of maximum?
View SolutionFigure 2.39 shows a photograph that illustrates the kind of interference fringes that can result when white light, which is a mixture of all colors, is used in Young's experiment, Except for the central fringe, which is white, the bright frings are a rainbow of colors. Why does Young's experiment separate white light into the constituent colors? In any group of colored fringes, such as the two singled out in the figure, why is red farther out from the central fringe than green is? And finally, why is the central fringe white rather than colored?

View SolutionWhite coherent light (400 nm-700 nm) is sent through the slits of a Young's double slit experiment. The separation between the slits is 05 mm and the screen is 50 cm away from the slits. There is a hole in the screen at a point 1.0 mm away (along the width of the fringes) from the central line. (a) Which wavelength(s) will be absent in the light coming from the hole ? (b) which wavelength(s) will have a strong intensity ?

View SolutionA coherent parallel beam of microwaves of wavelength `lambda = 0.5 mm` falls on a Young's double- slit apparatus. The separation between the slits is 1.0 mm. The intensity of microwaves is measured on a screen placed parallel to the plane of the slits at a distance of 1.0 m from it as shown in Fig. 2.42.
If the incident beam makes an angle or `30^(@)` with the x-axis (as in the dotted arrow shown in the figure), find the y-coordinates of the first minima on either side of the central maximum.
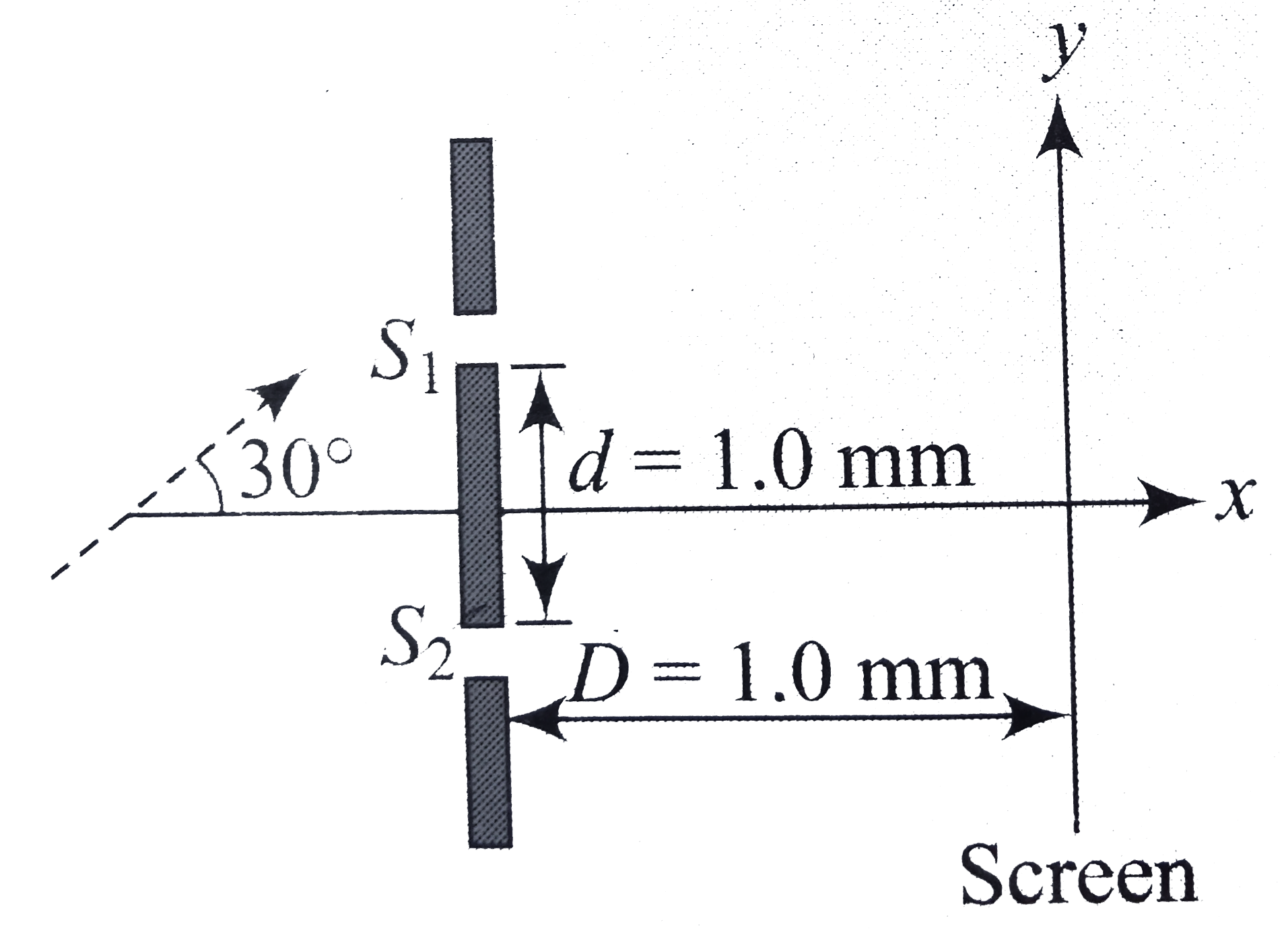
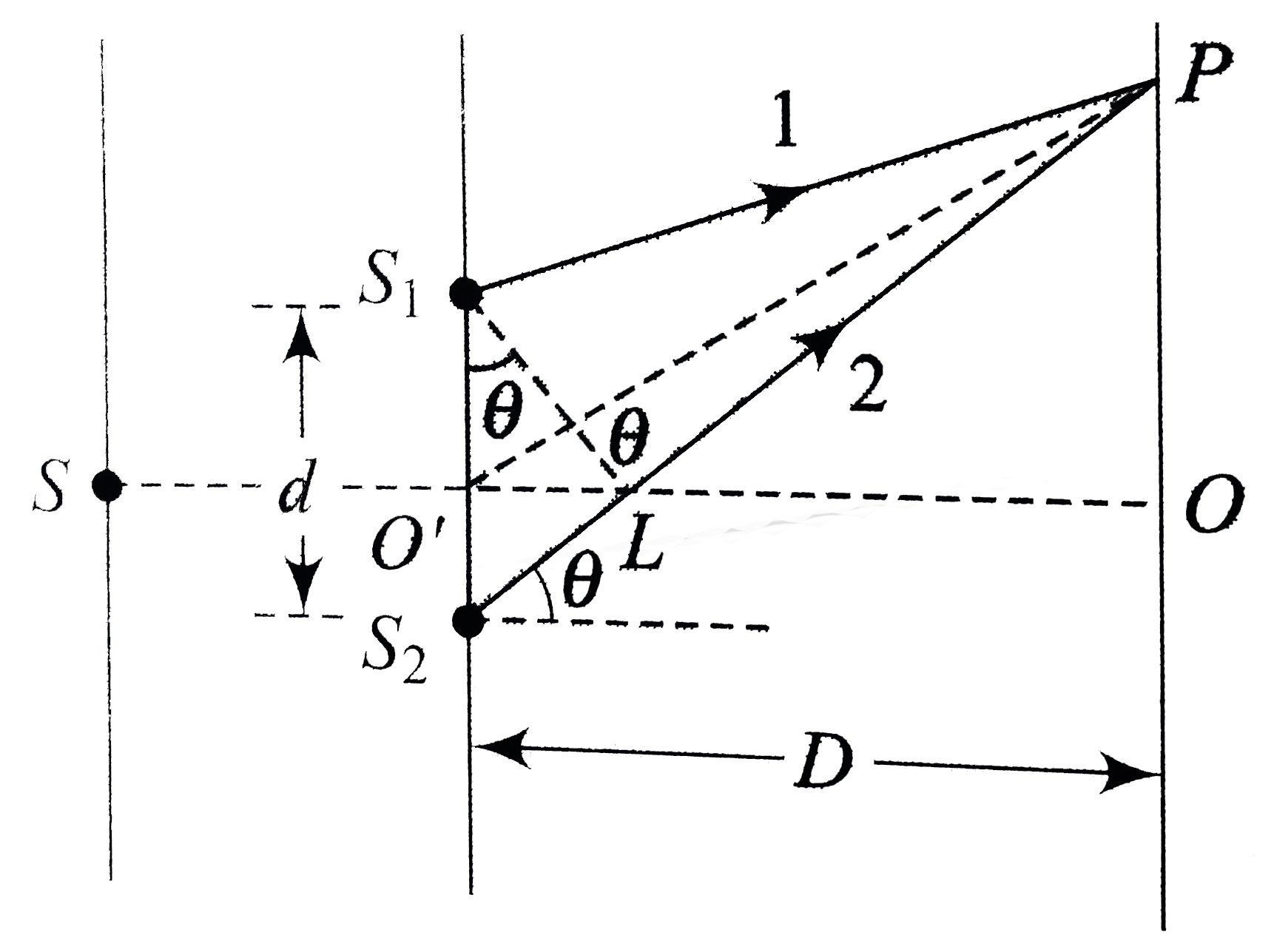
View SolutionIn Young's double-slit experiment, the point source is placed slightly off the central axis shown in Fig. 2.45.
a. Find the nature and order of the interference at point P.
b. Find the nature and order of the interference at point. O.

View SolutionThe wavelength of light coming from a sodium source is 589 nm. What will be its wavelength in water? Refractive index of water 1.33.`
View SolutionA Young's double slit apparatus is immersed in a liquid of refractive index `mu_(1).` The slit plame touches the liquid surface. A parallel beam of monochromatic light of wavelength `lambda` (in air) is incident normally on the slits.
a. Find the fringe width.
b. If one of the slits (say `S_(2)`) is covered by a transparent slab of refrative index `mu_(2)` and thickless t as shown, find the new position of central maxima.
c. Now, the other slit, `S_(1)` is also covered by a slab of same thickness and refractive index `mu_(3)` as shown in Fig. 2.49 due to which the central maxima recovers it positon, find the value of `mu_(3)`
Find the ratio of intensities at O in the three conditions (a), (b), and (c).
View SolutionA thin paper of thickness 0.02 mm having a refractive index 1.45 is pasted across one of the slits in a YDSE. The paper transimits `4//9` of the light energy falling on it.
a. Find the ratio of maximum intensity to the minimum intensity in interference pattern.
b. How many fringes will cross through the center if an indentical paper piece is pasted on the other slit also? The wavelength of the light used is 600 nm.
View SolutionA double slit apparatus is immersed in a liquid of refractive index 1.33. It has slit and the screen 1 mm. The slits are illuminated by a parallel beam of light whose wavelength in air is `6300 Å`
a. calculate the fringe width.
b. One of the slits of the apparatus is covered by a thin glass sheet of refractive index 1.53. Find the smallest thickness of the sheet to bring athe adjacent minima on the axis.
View SolutionA monochromatic light of `lambda = 500 Å` is incident on two identical slits separated by a distance of `5 xx 10^(-4)` m. The interference pattern is seen on a screen placed at a distance of 1 m from the plane of slits. A thin glass plate of thickness `1.5 xx 10^(-6)` m and refractive index `mu = 1.5` is placed between one of the slits and the screen . Find the intensity at the center of the screen.
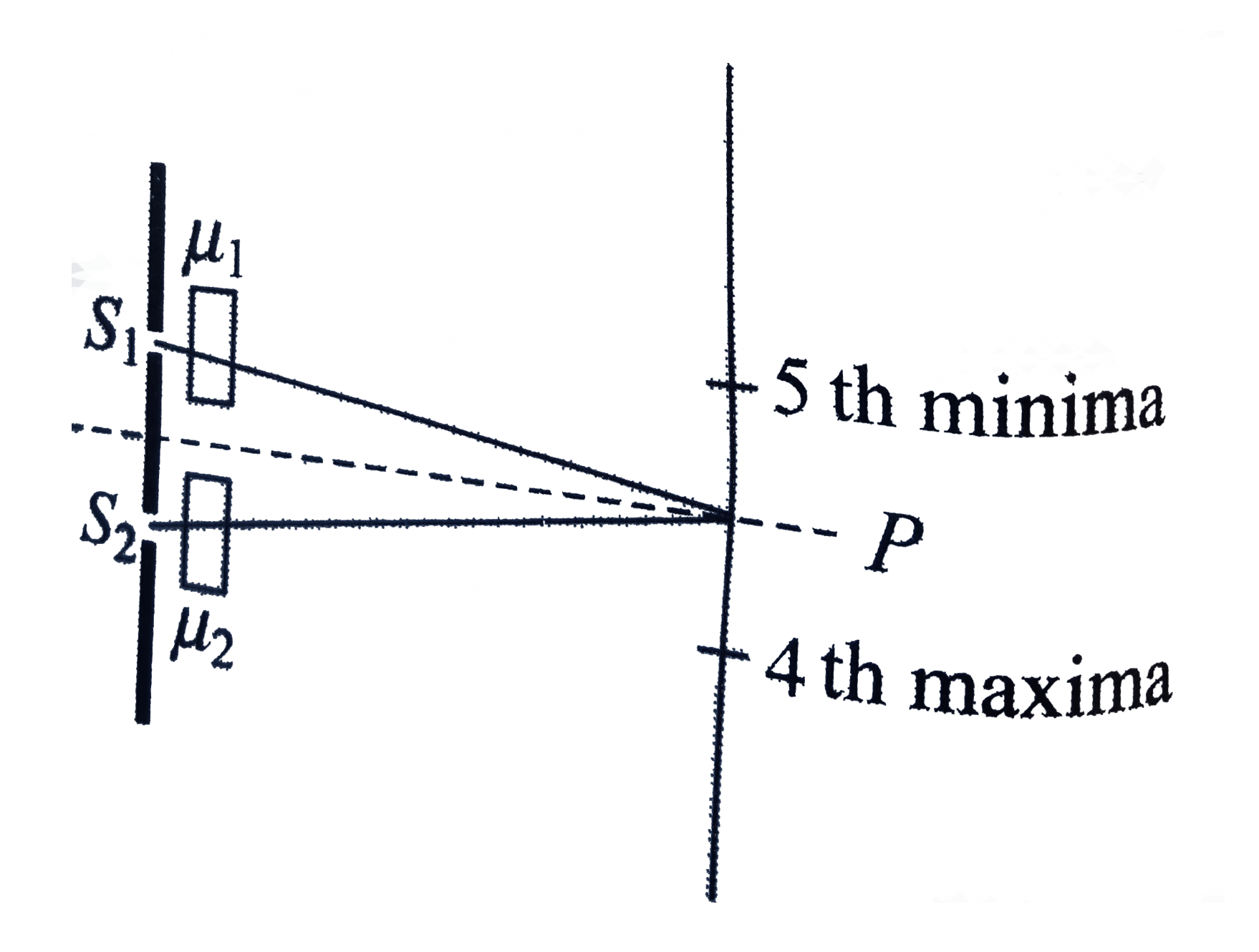
View SolutionIn Young's experiment the upper slit is covered by a thin glass plate of refractive index `1.4` while the lower slit is covered by another glass plate, having the same thickness as the first one but having refractive index `1.7` interference pattern is observed using light of wavelength `5400 Å`
It is found that point P on the screen where the central maximum `(n = 0)` fell before the glass plates were inserted now has `3//4` the original intensity. It is further observed that what used to be the fourth maximum earlier, lies below point P while the fifth minimum lies above P.
Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected.
 .
.
View SolutionA screen is at distance `D = 80` cm form a diagram having two narrow slits `S_(1)` and `S_(2)` which are `d = 2` mm apart.
Slit `S_(1)` is covered by a transparent sheet of thickness
`t_(1) = 2.5 mu m` slit `S_(2)` is covered by another sheet of thickness
`t_(2) = 1.25 mu m` as shown if Fig. 2.52.
Both sheets are made of same material having refractive index `mu = 1.40`
Water is filled in the space between diaphragm and screen. A monochromatic light beam of wavelength `lambda = 5000 Å` is incident normally on the diaphragm.
Assuming intensity of beam to be uniform, calculate ratio of intensity of C to maximum intensity of interference pattern obtained on the screen `(mu_(w) = 4//3)`

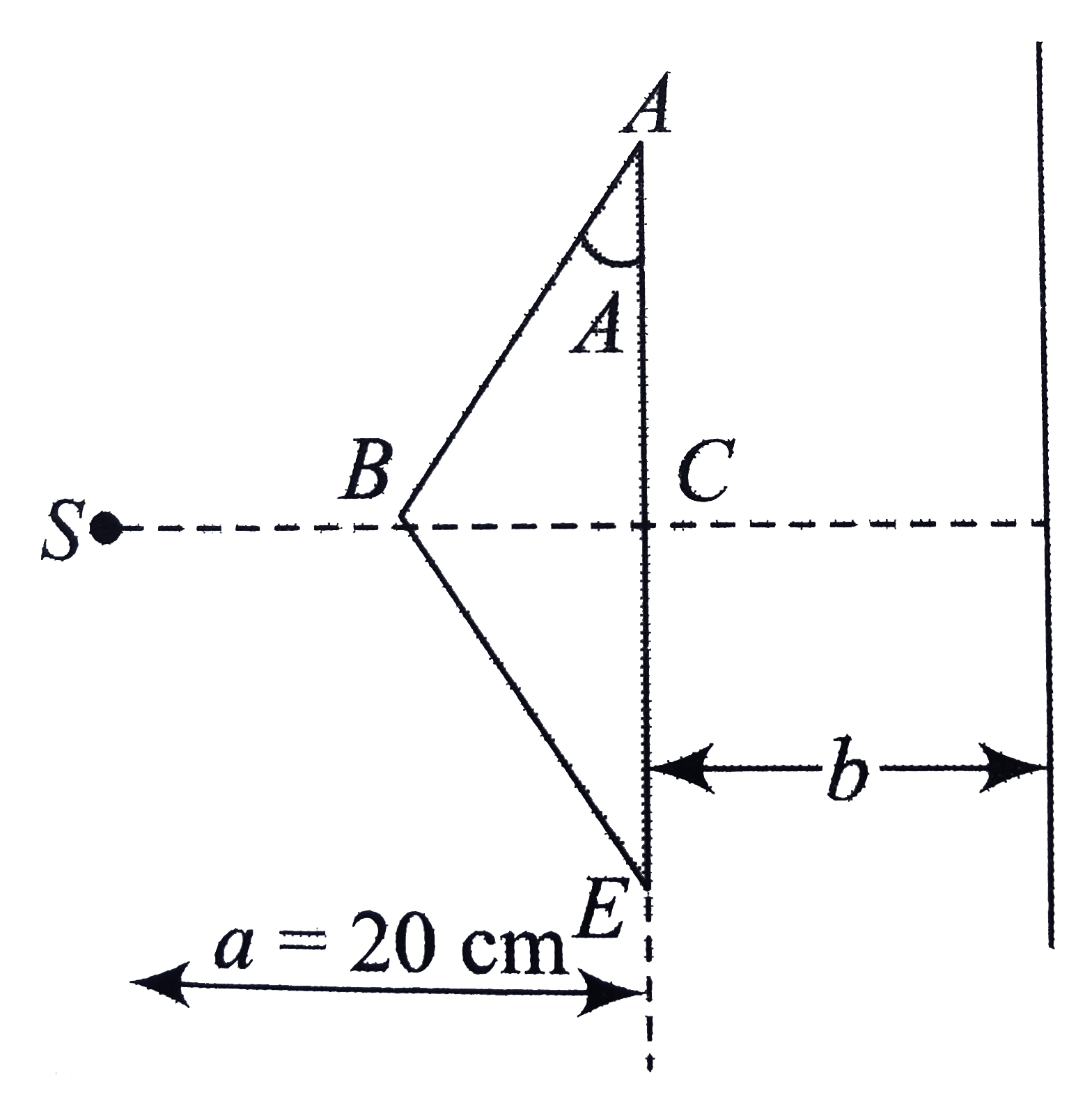
View SolutionTwo small angled transparent prisms (each or refracting angle `A = 1^(@))` are so placed that their bases coincide, so that common base is BC. This device is called Fresnel's biprism and is used to obtain coherent sources of a point source S illuminated by monochromatic light of wavelength `6000 Å` placed at a distance `a = 20` cm. Calculate the separation between coherent sources. If a screen is placed at a distance `b = 80` cm. from the device, what ist the finge which of fringes obtained (Refractive index of material of each prism `= 1.5.)`
View SolutionA Lloyd's mirror or length 5 cm is illuminated with mon ochromatic light of wavelength `lambda (= 6000 Å)` from a narrow 1 mm slit in its plane and 5 cm plane from its near edge. Find the fringe width on a screen 120 cm from the slit and width of interference pattern on the screen.

View Solution
Illustration questions and complete solutions for chapter WAVE OPTICS of CENGAGE PHYSICS (HINGLISH) of Class 12