Complete Solutions to Solved Examples of chapter MAGNETICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MAGNETICS |
| DC PANDEY | Solved Examples |
| Number Of Questions | 60 |
| Academic Year | 2023-24 |
A charged particle projected in a magnetic field
`B=(3hati+4hatj)xx10^-2T`
The acceleration of the particle is found to be
`a=(xhati+2hatj)m/s^2`
find the value of `x`
View SolutionWhen as proton has a velocity `v=(2hati+3hatj)xx10^6m/s`, it experience a force `F=-(1.28xx10^-13hatk)` When its velocity is along the z-axis, it experience a force along the `x`-axis. What is the magnetic field?
View SolutionA magnetic field of `(4.0xx10^-3hatk)T` exerts a force `(4.0hati+3.0hatj)xx10^-10N` on a particle having a charge `10^-9C` and moving in te `x-y` plane. Find the velocity of the particle.
View SolutionTwo particles `A` and `B` of masses `m_A` and `m_B` respectively and having the same charge are moving ina plane. A uniform magnetic field exists perependicular to this plane. The speeds of the particles are `v_A` and `v_B` respectively and the trajectories are as shown in the figure. Then,

View SolutionA proton a deuteron and an `alpha` - particle having the same kinetic energy are moving in circular trajectories in a constant magnetic of the trajectories of these particle, then
View SolutionTwo particles `X` and `Y` having equal charges, after being acceleration through the same potential difference, enter a region of uniform magnetic field and describe circular paths of radii `R_1` and `R_2`, respectively. The ratio of the mass of `X` to that of `Y` is
View SolutionA horizontal rod `0.2 m` long is mounted on a balnce and carries a current. At the location of the rod a uniform horizontal magnetic field has magnitude `0.067 T` and direction perpendicular to the rod. The magnetic force on the rod is measured by the balance and is found to be `0.13N`. What is the current?
View SolutionA square of side `2.0 m` is placed in a uniform magnetic field `B=2.0 T` in a direction perpendicular to the plane of the square inwards. Equal current `i=3.0 A` is flowing in the directions shown in figure. Find the magnitude of magnetic force on the loop.

View SolutionIn the figure shown a semicircular wire loop is placed in a uniform magnetic field `B=1.0T`. The plane of the loop is perpendicular to the magnetic field. Current `i=2A` flows in the loop in the directions shown. Find the magnitude of the magnetic force in both the cases `a` and `b`. The radius of the loop is 1.0 m

View SolutionA square loop `OABCO` of side of side `l` carries a current `i`. It is placed as shown in figure. Find the magnetic moment of loop.

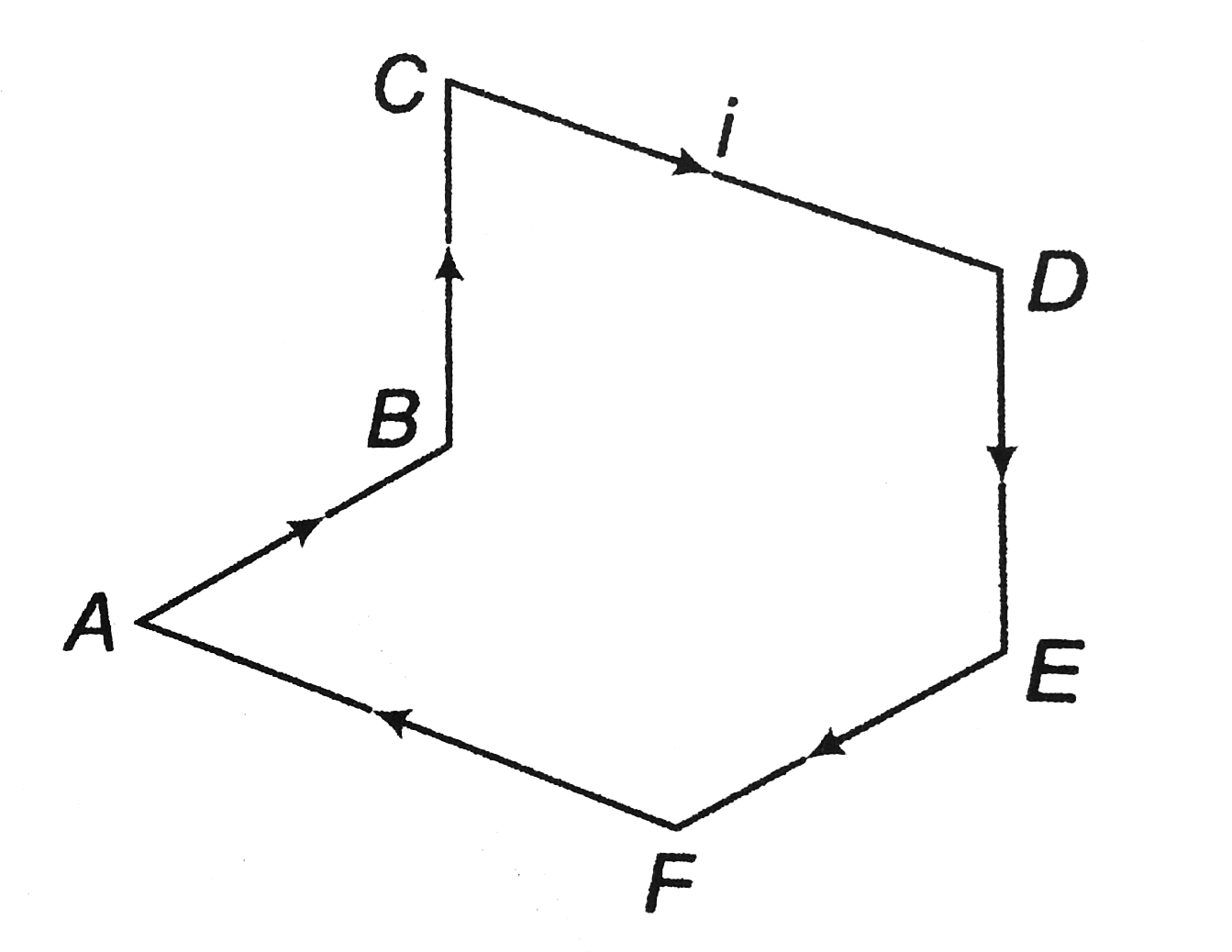
View SolutionFind the magnitude of magetic moment of the current carrying lop `ABCDEFA`. Each side of the loop is `10 cm` long and current in the loop is `i=2.0A`
View SolutionA circular loop of radius `R=20` cm is placed in a uniform magnetic field `B=2T` in `xy`-plane as shown in figure. The loop carries a current `i=1.0 A` in the direction shown in figure. Find the magnitude of torque acting on the loop.

View SolutionIn a high tension wire electric current runs from eash to west. Find the direction of magnetic fielsd at points above and below the wire.
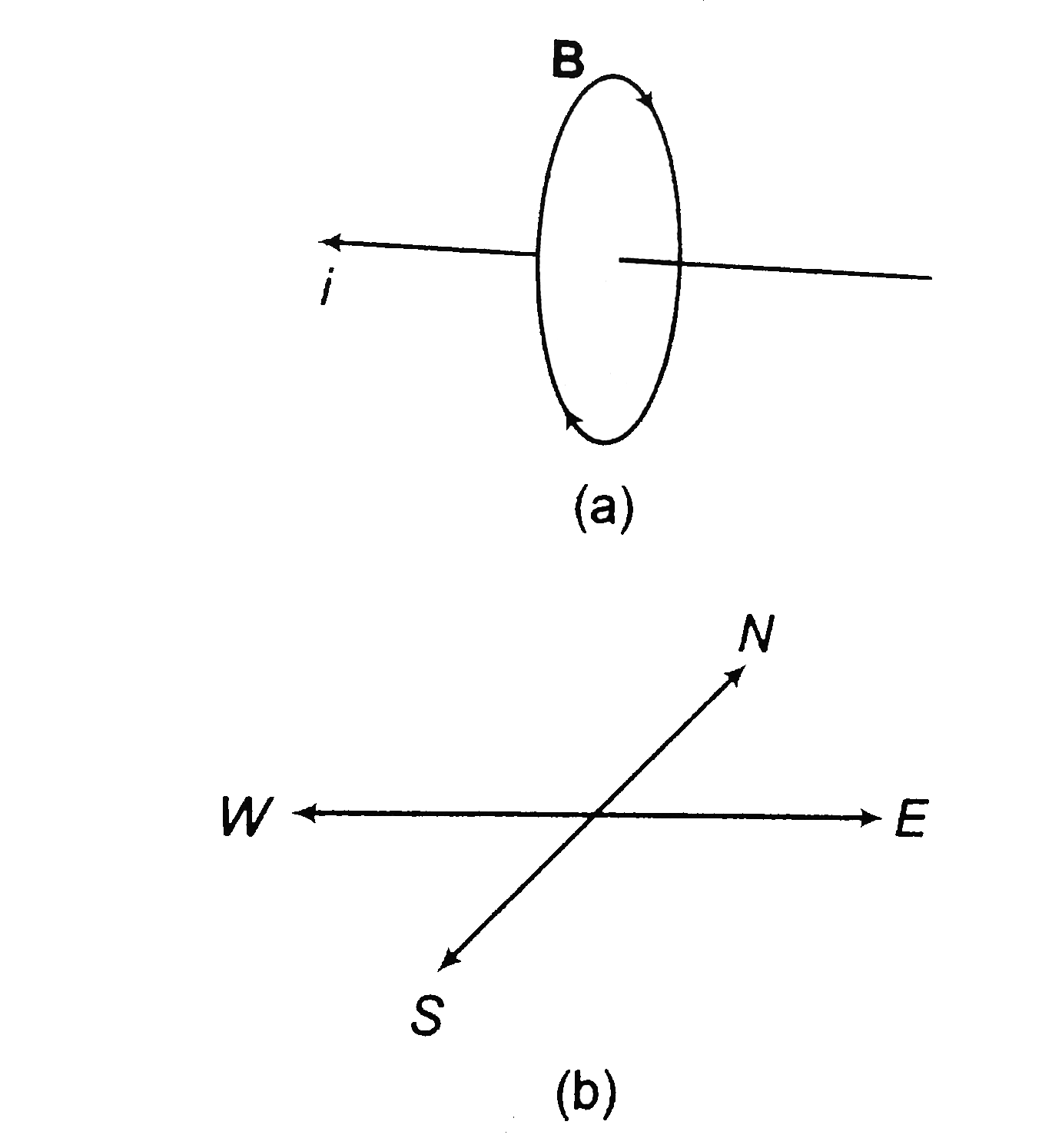
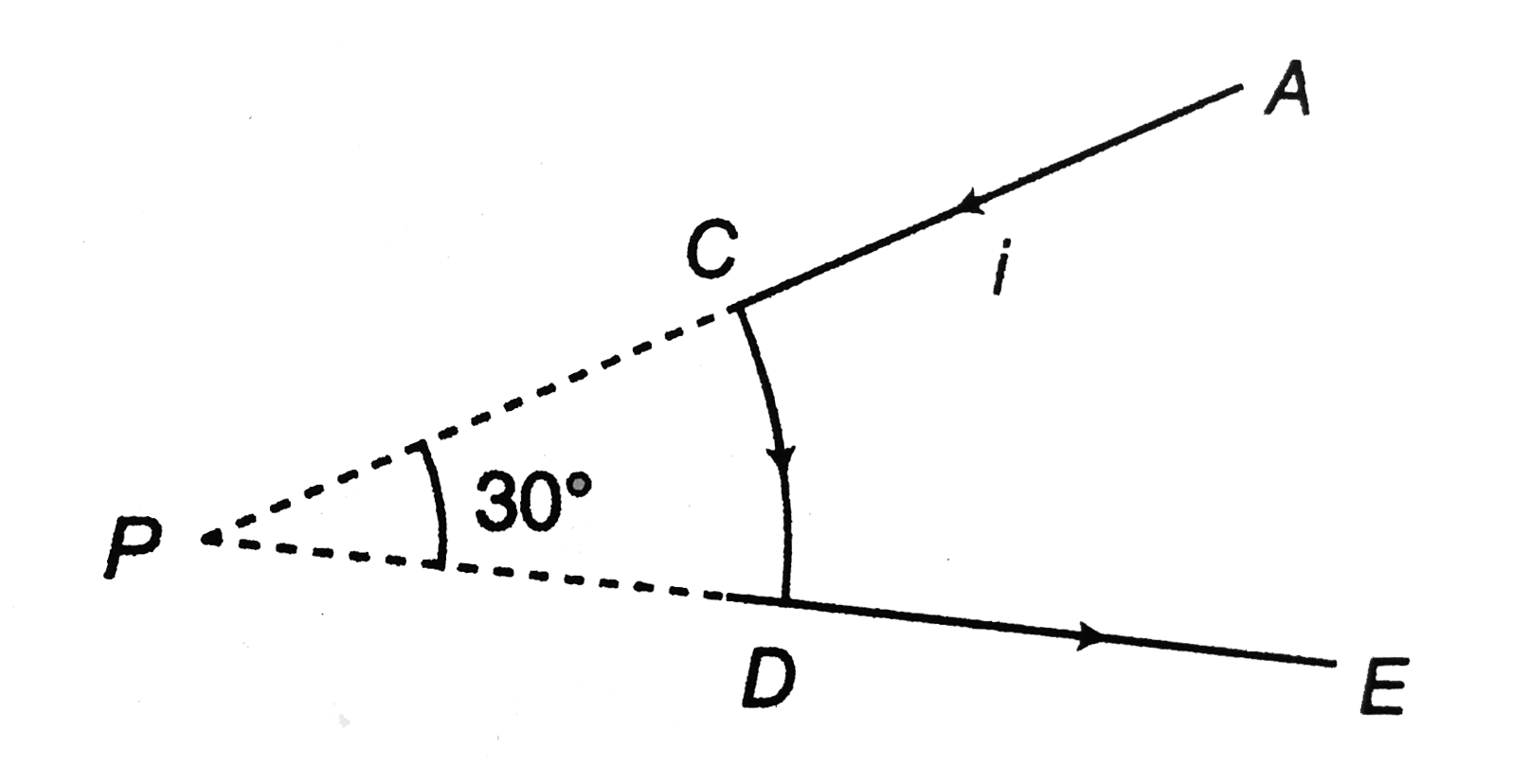
View SolutionA current path shaped as shown in figure produces a magnetic field at `P`, the centre of the arc. If the arc subtends an angle of `30^@` and the radius of the arc is `0.6 m`, what are the magnitude and direction of the field produced at P if the current is `3.0 A`.
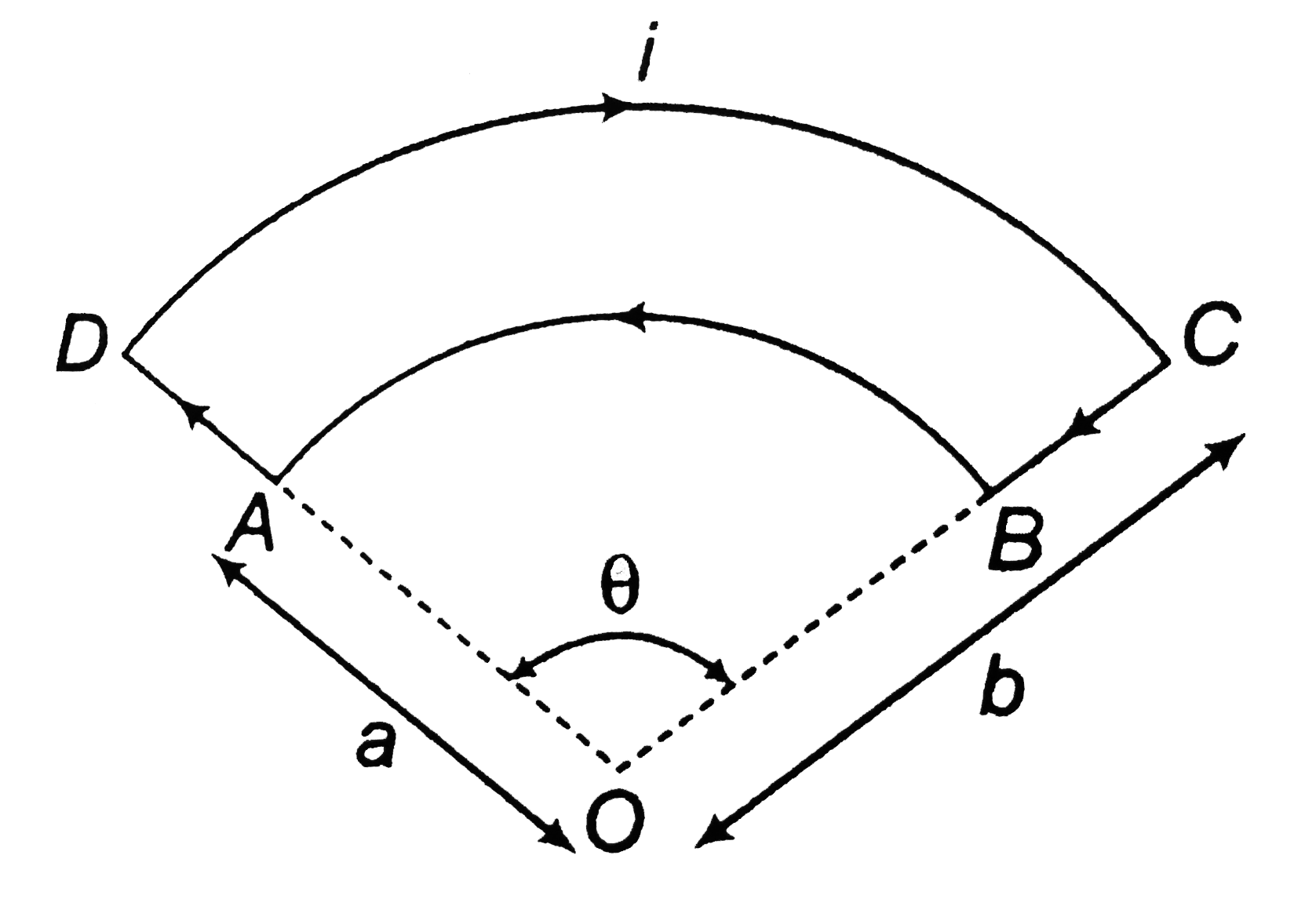
View SolutionFigure shows a current loop having two circular arcs joined by two lines. Find the magnitude field `B` at the centre `O`.
View SolutionThe magnetic field `B` due to a current carrying circular loop of radius `12cm` at its centre is `0.5xx10^-4T`. Find the magnetic field due to this loop at a point on the axis at a distance of `5.0cm` from the centre.
View SolutionA closed cure encircles several conductors. The line integral `intB.dI` around this curve is `3.83xx10^-7T-m`
a. What is the net current in the conductors?
b. If you were to integrate aroundthe curve in the opposite direction, what would be the value of the line integral?
View SolutionAn infinitely long hollow conducting cylinder with inner radius `(R)/(2)` and outer radius `R` carries a uniform current density along its length . The magnitude of the magnetic field , ` | vec(B)|` as a function of the radial distance `r` from the axis is best represented by
View SolutionA device called a toroid (figure) is often used to create an almost uniform magetic fiedl in some enclosed area. The device consists of a conducting wire wraped around a ring (a torus) made of a non conducting material. For a toroid having `N` closely spaced turns of wire, calculate the magnetic field in the region occupied by the torus, a distasnce `r` from the centre.
View SolutionTwo long parallel wires are separated by a distance of `2.50 cm`. The force per unit length that each wire exerts on the other is `4.00xx10^-5 N/m`, and the wires repel each other. The current in one wire is `0.600A`.
a. What is the current in the second wire ?
b. Are the two currents in the same direction or in opposite direction?
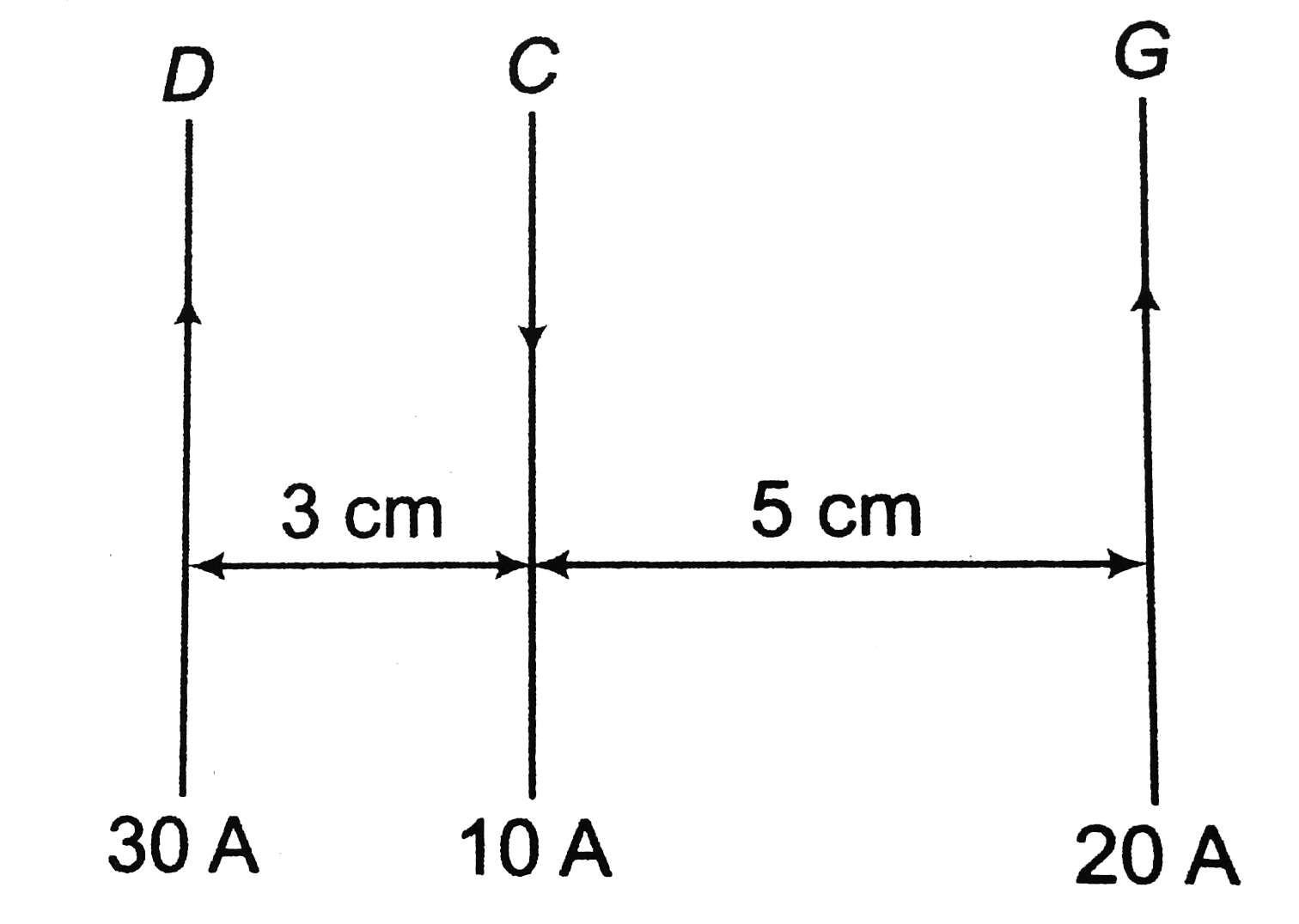
View SolutionConsider three long straight parallel wire as shown in figure. Find the force experienced by a `25 cm` length of wire `C`.
View SolutionCalculate the magnetic induction (or magnetic field) at a point 1A away from a proton, measured along its ais of spin. The magnetic moment of the proton is `1.4xx10^-26A-m^2`
View SolutionA bar magnet of magnetic moment `2.0` `A-m^2` is free to rotate about a vertical axis through its centre. The magnet is released from rest from the east west position. Find the kinetic energy of the magnet as it takes the north south position. The horizontal component of the earth's magnetic field as `B=25muT`. Earth's magnetic field is from south to north.
View SolutionIn the magnetic meridian of a certain place, the horizontal component of earth's magnetic fied is `0.26 G` and the dip angle is `60^@`. Find
a. Vertical component of earth's magnetic field
b. the net magnetic field at this place
View SolutionA magnet suspended at `30^@` with magnetic meridian makes an angle of `45^@` with the horizontal. What shall be the actual value of the angle of dip?
View SolutionA short bar magnet is placed with its north pole pointin north. The neutral point is `10 cm` away from the centre of the magnet. If `H=0.4G`, calculate the magnetic moment of the magnet.
View SolutionA magnetic needle performs `20` oscillations per minute in a horizontal plane. If the angle of dip be `30^@`, then how many oscillation per minute will this needle perform in vertical, north south plane and in vertical east -west plane?
View SolutionA rectangular coil of area `5.0xx10^-4m^2` and `60` turns is pivoted about one of its vertical sides. The coil is in a radial horizontal magnetic field of `9xx10^-3T`. What is the torsional constant of the spring connected to the coil if a current of `0.20mA` produces an angular deflection of `18^@`?
View SolutionThe region between `x=0` and `x=L` is filled with uniform steady magnetic field `B_0hatk`. A particle of mass m, positive charge q and velocity `v_0hati` travels along x-axis and enters the region of the magnetic field. Neglect the gravity throughout the question.
a. Find the value of `l` if the particle emerges from the region of magnetic field with its final velocilty at an angel `30^@` to its initial velocity.
b. Find the final velocity of the particle and the time spent by it in the magnetic field, if themagnetic field now extends upto 2.1`L`.
View SolutionA particle of specific charge alpha enters a uniform magnetic field `B=-B_0hatk` with velocity `v=v_0hati` from the origin. Find the time dependence of velocity and position of the particle.

View SolutionA particle of specific charge `alpha` is projected from origin with velocity `v=v_0hati-v_0hatk` in a uniform magnetic field `B=-B_0hatk`. Find time dependence of velocity and position of the particle.
View SolutionA charged particle `(q,m)` enters uniform magnetic field B at angle `alpha` shown in figure with speed `v_0`. Find
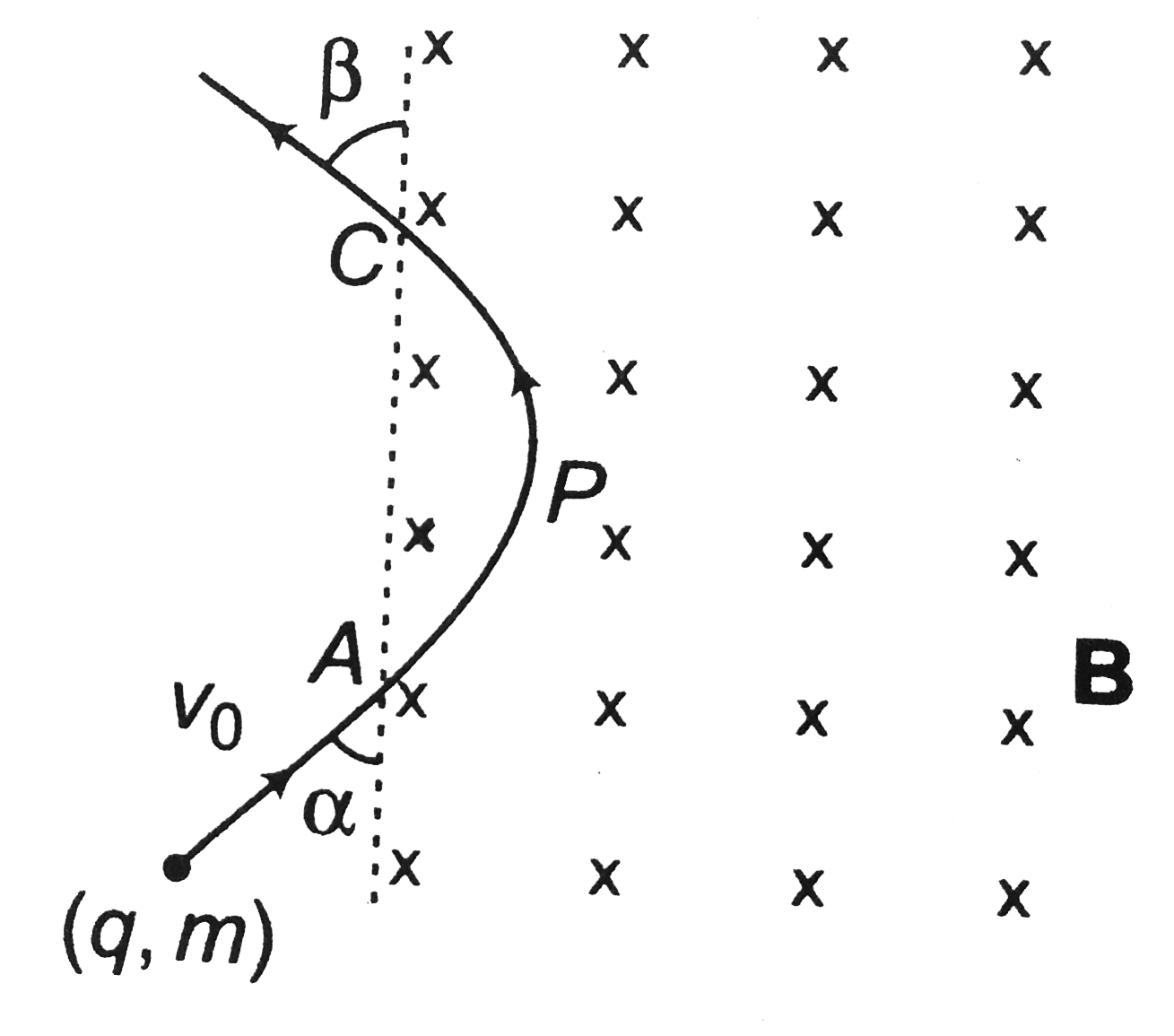
a. The angle `beta` at which it leves the magnetic field
b. time spent by the particle in magnetic field and
c. the distance `C`.
View SolutionA particle of mass `m=1.6xx10^-27` kg and charge `q=1.6xx10^-19C` enters a region of uniform magnetic field of stregth `1 T` along the direction shown in figure. The speed of the particle is `10^7 m//s`

a. The magnetic field is directed along the inward normal to the plane of the paper. The particle leaves the region of the fiedl at the point `F`. Find the distasnce `EF` and the angle theta.
b. If the direction of the field is along the outward normal to the plane of the paper find the time spent by the particle in the regin of the magnetic field after entering it at `E`.
View SolutionAn electron gun `G` emits electons of energy `2 keV` travelling in the positive x-direction. The electons are required to hit the spot `S` where `GS=0.1 m`, and the line `GS` makes an angle of `60^@` with the x-axis as shown in figure. A uniform magnetic field `B` parallel to `GS` exists in the region outside the electron gun.

find the minimum value of `B` needed to make the electrons hit `S`.
View SolutionA wire shaped to a regular hexagon of side `2 cm` carries a current of `2A`. Find the magnetic field at the cetre of the hexagon.
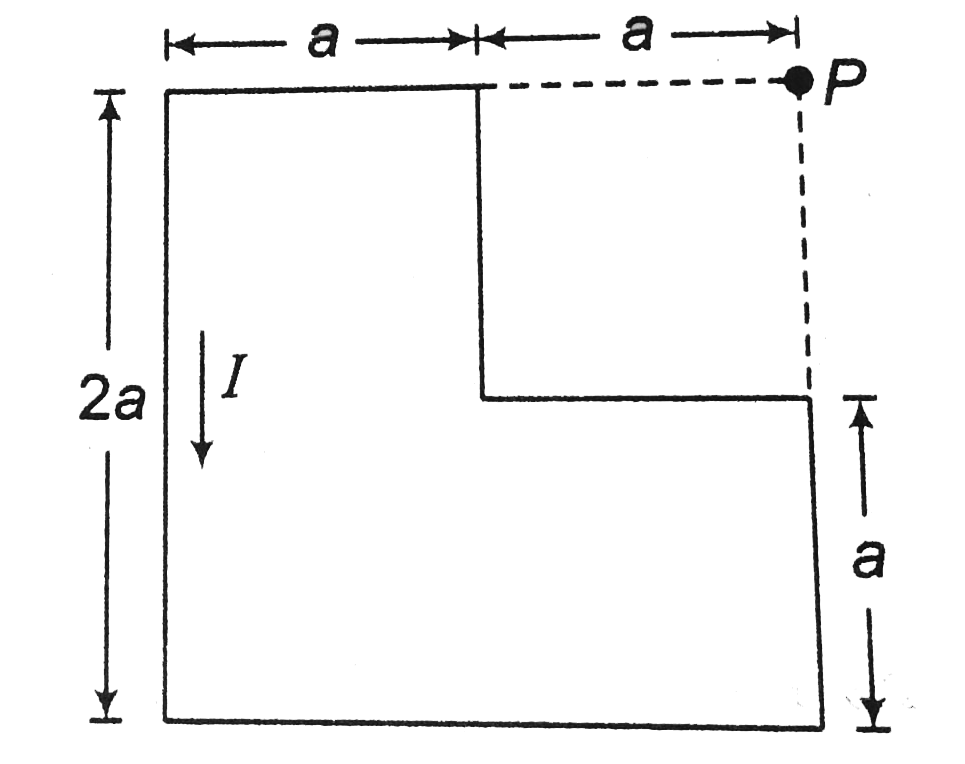
View SolutionFind the magnetic field `B` at the point `P` in figure
View SolutionA long insulated copper wire is closely wound as a spiral of `N` turns. The spiral has inner radius a and outer radius `b`. The spiral lies in the `xy`-plane and a steady current I flows through the wire. The`z`-component of the magetic field at the centre of the spiral is

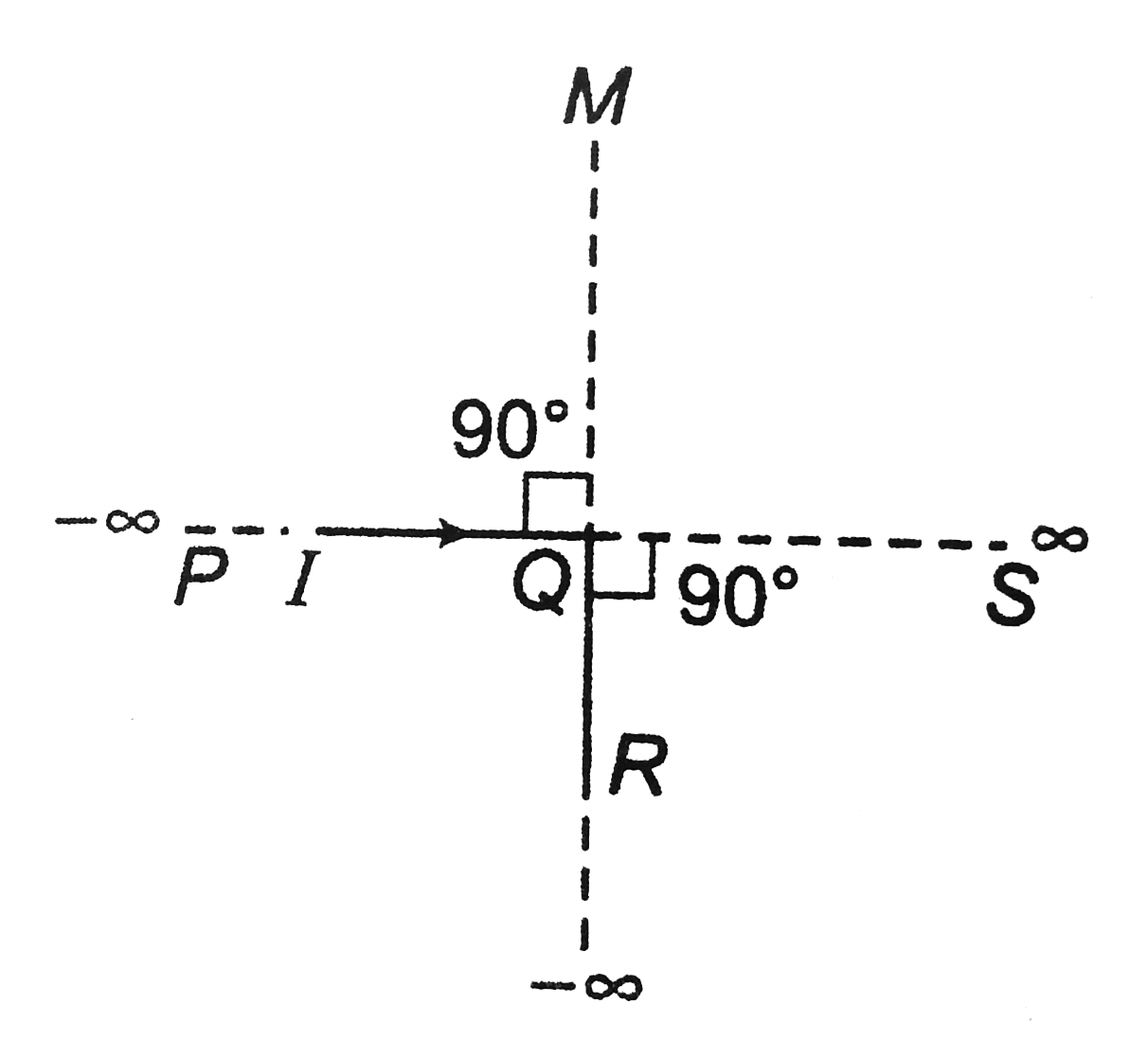
View SolutionAn infifnitely long conductor `PQR` is bent to form a right angle as shown in figure. A current `I` flows through `PQR`. The magnetic field due to this current at the point `M` is `H_1` Now, another infinitely long straight conductor `QS` is connected at `Q`, so that current is `I/2` in `QR` as well as in `QS`, the current in `PQ` remaining unchanged. The magnetic field at `M` is now `H_2`. The ratio `H_1/H_2` is given by `
View SolutionA long horizontal wire `AB`,which is free to move in a vertical plane and carries a steady current of `20 A`, is in equilibrium at a height of `0.01 m` over another paralllel long wire `CD` which is fixed in a horizontal plane and carries a steady current of `30 A`, as shown in figure. Show that when `AB` is slightly
depressed it executes simple harmonic motion. Find the period of oscillations.

View SolutionA straight segment `OC` (of lengh `L`) of a circuit carrying a current I is placed along the x-axis. Two infinitely long straight wire `A` and `B` each extending from `z=-ooto+oo` are fixed at `y=-a` and `y=+a` respectively as show in the figure. If the wires `A` and `B` each carry a current I into the plane of the paper, obtain the expression for the force acting on the segment `OC`. What will be the force on `OC` if the current in the wire `B` is reversed?
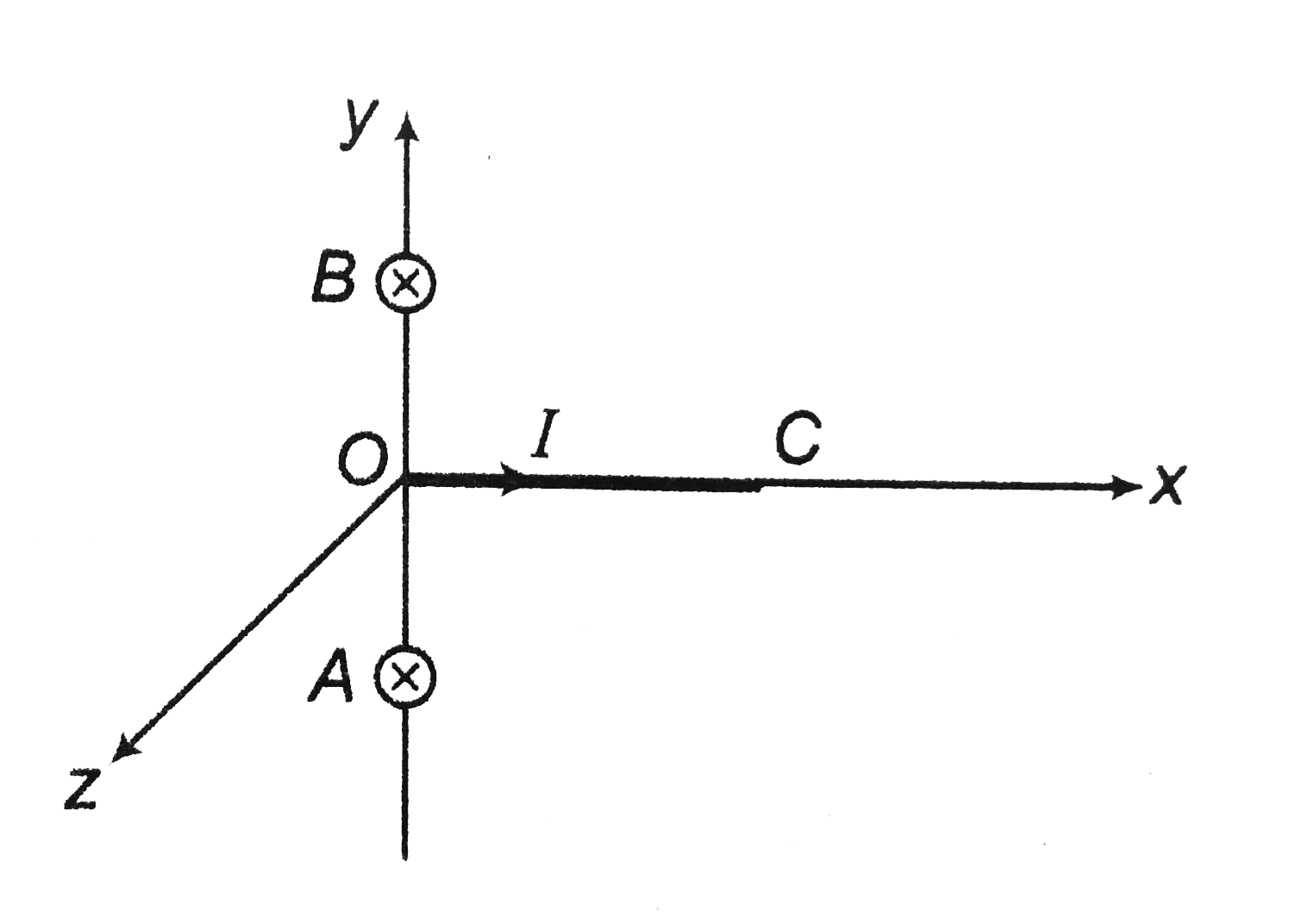
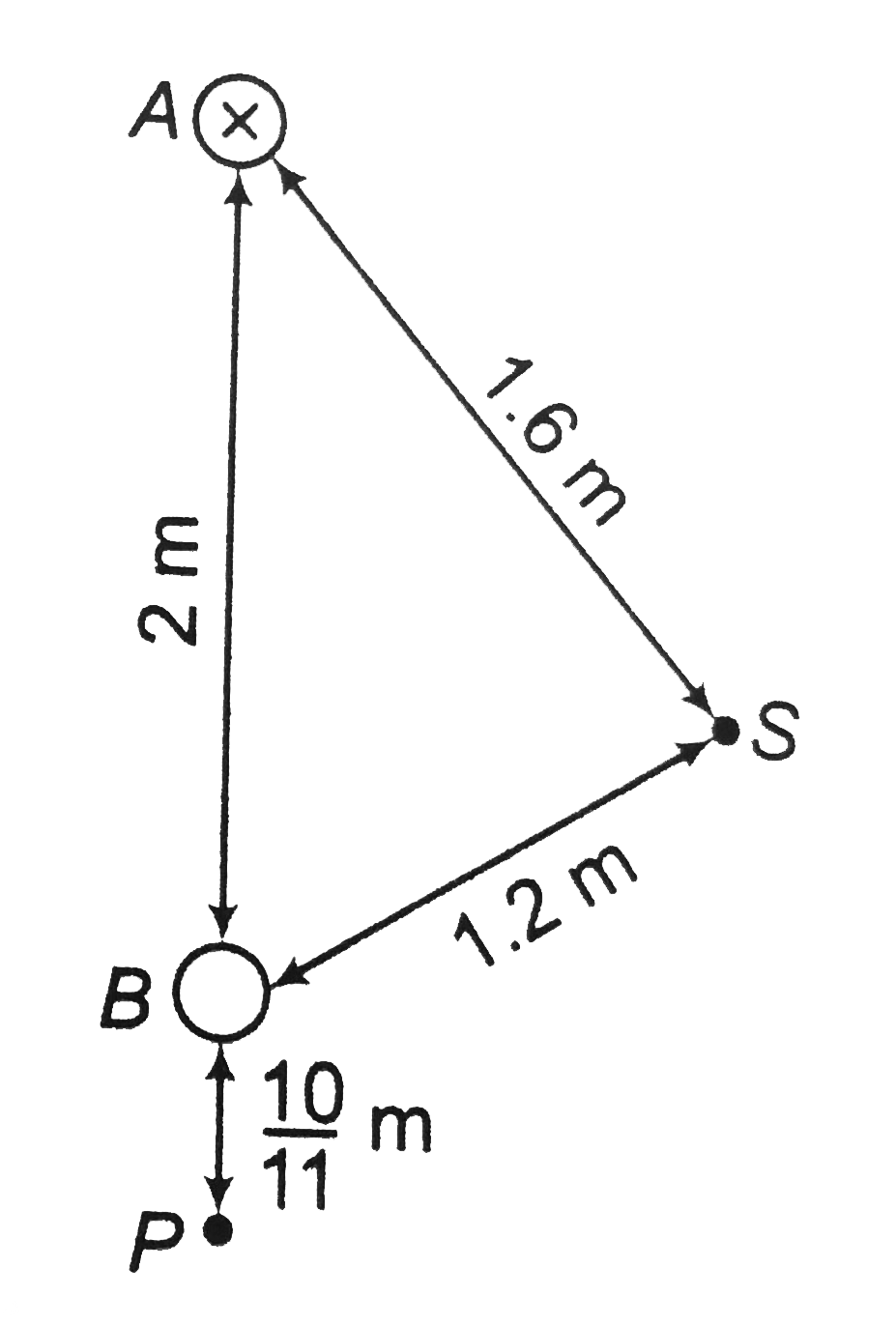
View SolutionTwo long straight parallel wieres are `2m` apart, perpendicular to the plane of the paper. The wire A carries a current of `9.6 A`, directed into the plane of the paper. The wire `B` carries a current such that the magnetic field of induction at the point `P`, at a distance of `10/11` m from the wire B, is zero. find
a. the magnitude and directiion of the current in B.
b. the magnitude of the magnetic field of induction of the pont `S`.
c. the force per unit length on the wire `B`.
View SolutionA current of `10 A` flows around a closed path in a circuit which is in the horizontal plane as shown in the figure. The circuit consists oi eight alternating arcs of radii `r_1=0.08m` and `r_2 =0.12m`. Each subtends the same angle at the centre.
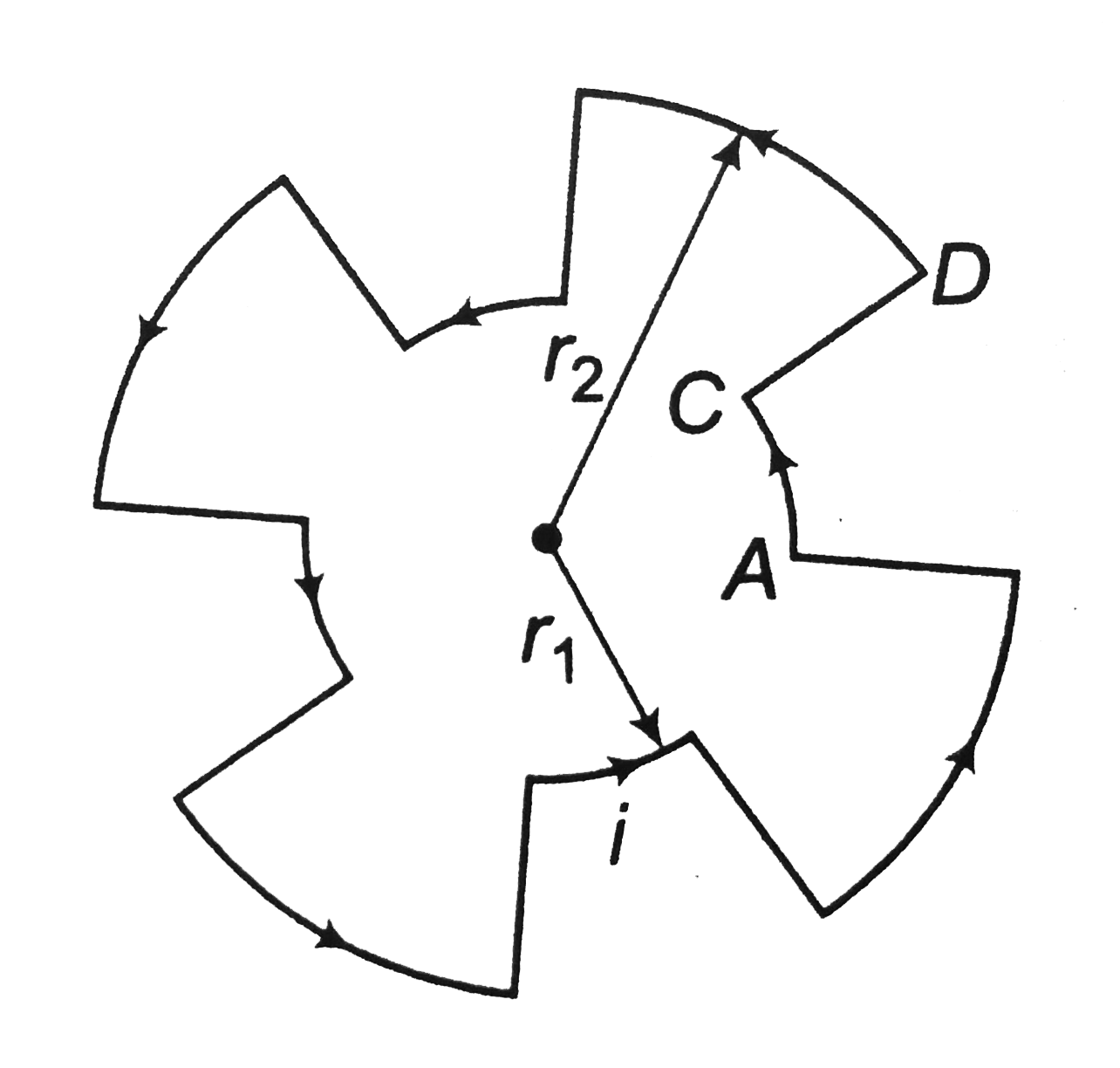
a. Find the magnetic field produced by this circuit at the centre.
b. An infinitely long straight wire carrying as current of `10 A` is passing through the centre of the above circuit vertically with the direction of the current being into the pane of the circuit. what is the force acting on the wire at the centre due to the current in the circuit? What is the force acting on the arc `AC` and the straight segment `CD` due to the current at the centre?
View SolutionConsider the motion of a positive point charge in a region where there are simultaneous uniform eletric and magnetic field `E=E_0hatj` and `B=B_0hatj`. At time `t=0`, this charge has velocity v in the x-y-plane making an angle `theta` with the x-axis. Which of the following option(s) is (are) correct for time `tgt0?`
a. If `theta=0^0` the charge moves in a circular path in the xy-plane.
`b.If theta=0^0` the charge undergoes helical motion with constant pitch along the y-axis.
c. If `theta=1 0^0` the charge undergoes helicalmotion with its pitch increasing with time along the `y`-axis.
d. If `theta=90^@` the charge undergoes linear but accelerated motion along the `y`-axis.
View SolutionA particle of charge `+q` and mass `m` moving under the influence of as uniform electric field `Ehati` and uniform magnetic field `B hatk` follows trajectory form `P` to `Q` as shown in figure. The velocities at P and Q re `vhati and -2hatj`. Which of the following statement(s) is/are correct?
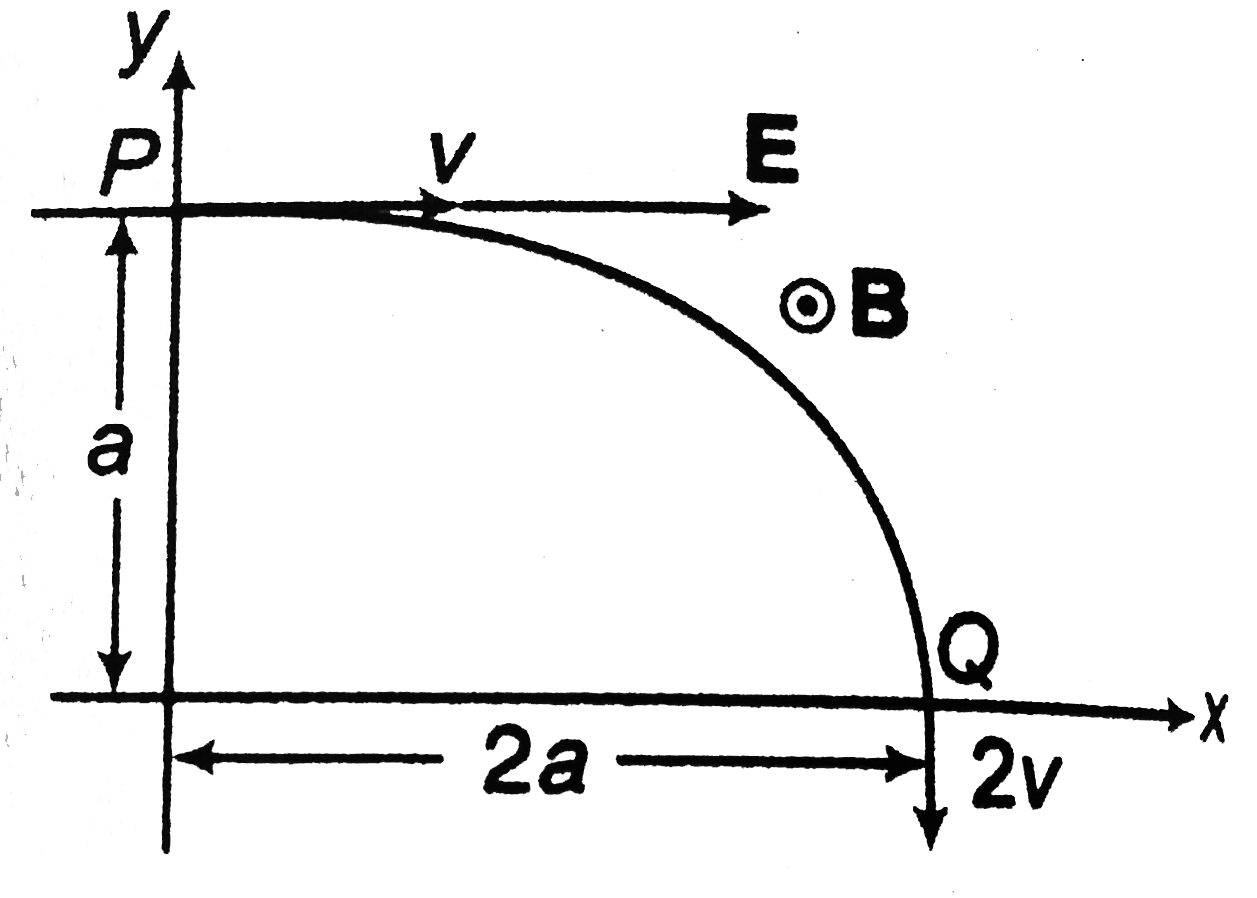
`a. E=3/4[(mv^2)/(qa)]`
b. Rate of work done by the electrif field at P is `3/4[(mv^3)/a]`
c. Rate of work done by the electric field at `P` is zero.
d. Rate of work done by both the field at `Q` is zero.
View SolutionA proton moving with a constant velocity passes through a region of space without any changing its velocity. If `E` and `B` represent the electric and magnetic fields, respectively. Then, this region of space may have
View SolutionA wire loop carrying a current `I` is placed in the `xy`-plane as shown in figure
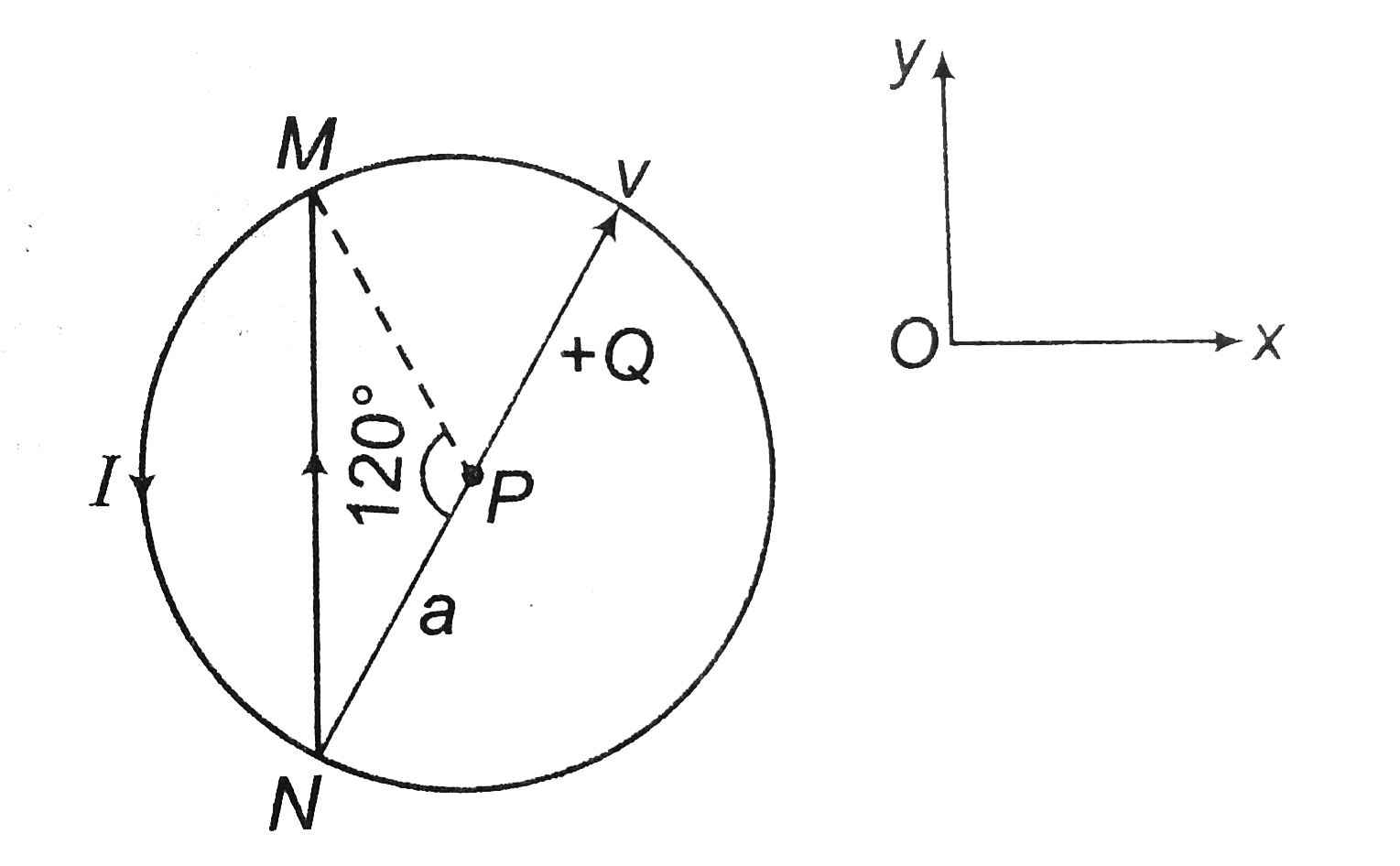
a. If a particle chsarge +Q and mass m is placed at in centre `P` and given a velocity `v` along `NP` (see figure), find its instaneous acceleration.
If an external uniform magnetic induction field `B=Bhati` is applied, find the force and the torque acting on the loop due to this field.
View SolutionTwo long parallell wires carrying currents `2.5 A` and `I` (ampere) in the same directon (directed into theplane of the paper) are held at `P` and `Q`, respectively such that they are perpendicular to the plane of paper. The points `P` and `Q` are located at distance of `5 m` and `2m` respectively from a collinear point `R` (see figure).
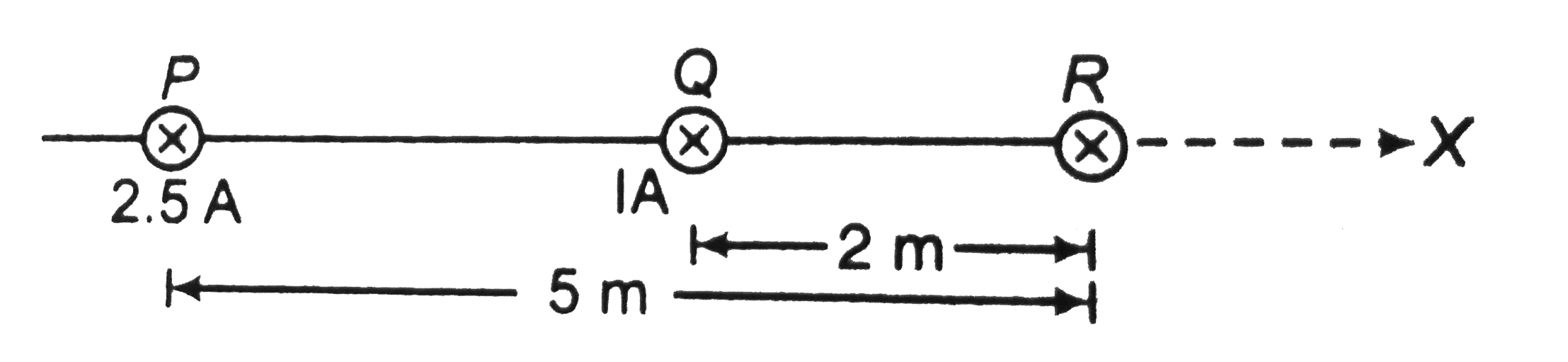
a. An electron moving with a velocity of `4xx10^5` m/s along the positive x-directionn experieces a force of magnitude `3.2xx10^-20` `N` at the point `R`. Find the volume of `I`.
b. Find all the positions at which a third long paralle wire carryig a current of magnitude `2.5 AS` may be placed, so that the magnetic induction at `R ` is zero.
View SolutionWhen `Euarr uarrB`e and particle velocity is perpendicuular to both of these field.
View SolutionWhen `E_|_B` and the particle is released at rest from origin.
View SolutionA cyclotron's oscillator frequency is `10MHz`. What should be the operating magnetic field fro accelerating protons? If the radius of its dees is `60cm`, what is the kinetic energy (in `MeV`) of the proton beam produced by the acceleration?
`(e-1.60xx10^-19C,m_p=1.67xx10^-27kg, 1MeV=1.6xx10^-13J)`
View SolutionA charged particle carrying charge `q=1muc` moves in uniform magnetic with velocity `v_1=10^6m//s` at angle `45^@` with `x`-axis in the `xy`-plane and experiences a force `F_1=5sqrt2N` along the negative `z`-axis. When te same particle moves with velocity `v_2=10^6m//s` along the `z`-axis it experiences a force `F_2` in `y`-direction. Find
a. the magnitude and direction of the magnetic field
b. the magnitude of the force `F_2`.
View SolutionA matel wire PQ of mass 10g lies at rest on two horizontal metal rails separated by 4.90 cm . A vertically downward magnetic field of magnitude 0.800 T exists in the space. The resistance of the circuit is slowly decreased and it is found that when the resistance goes below`20.0 Omega`, the wire PQ starts sliding on the rails. Find the coefficient of friction.

View SolutionWhat is the value of `B` that can be set up at the equator to permit a proton of speed `10^7m//s` to circulate around the earth?
`[R=6.4xx10^6m,m_p=1.67xx10^-27kg]`
View SolutionDeuteron in a cyclotron describes a circle of radius `32.0cm`. Just before emerging from the `D's`. The frequency of the applied alternating voltage is `10MHz`. Find
a. the magnetic flux density (i.e. the magnetic field).
b. the energy and speed of the deutron upon emergence.
View SolutionIn the Bohr model of the hydrogen atom, the electron circuulates around the nucleus in a path of radius `5xx10^-11m` at a frequency of `6.8xx10^15Hz`.
a. What value of magnetic field is set up at the centre of the orbit?
b. What is the equivalent magnetic dipole moment?
View SolutionA flat dielectric disc of radius `R` carries an exces charge on its surface. The surface charge density `sigma`. The disc rotastes about an axis perpendicular to its lane passing thrugh the centre with angulasr velocity `omega`. Find the toruque on the disc if it is placed in a uniform magnetic field `B` directed perpendicular to the rotation axis.
View SolutionThree infinitely long thin wires, each carrying current i in the same dieretion, are the xy plane of a gravity free space. The central wire is along the y-axis while the other two are along `x=+-d`
i find the locus of the points for which the magnetic field `B` is zero.
ii If the central wire is displaced along the `z`-direction by a small amount and released, show that it will execute simple harmonic motion. If the linear mass density of the wires is `lamda`, find the frequency of oscillation.
View SolutionUniform electrilcf and magnetic fields with strength E and B are directed along of x-axis. A particle with specific charge `q/m` leves the origin in the direction of x-axis with an initial velocity `v_0`. Find
a. the y-coordinate of the particle when it crosses the y-xis for nth time.
b. the angle `alpha` between the particle's velocity vector adn the y-axis for nth time
View SolutionA current is passing through a cylindrical conductor with a hole (or cavity) inside it. Show that the magnetic field inside the hole is uniform and find its magnitude and direction.
View SolutionA particle of charge `q` and mass `m` is projected from the origin with velocity `v=v_0 hati` in a non uniformj magnetic fiedl `B=-B_0xhatk`. Here `v_0` and `B_0` are positive constants of proper dimensions. Find the maximum positive x coordinate of the particle during its motion.
View Solution
Solved Examples questions and complete solutions for chapter MAGNETICS of DC PANDEY ENGLISH of Class 12