Complete Solutions to Exercise of chapter MAGNETICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MAGNETICS |
| DC PANDEY | Exercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Write the dimensions of `E/B`. Here, `E` is the electric field and B the magnetic field.
View SolutionIn the relation `F=q(VxxB),` which paiers are always perpendicular to each other.
View SolutionIf a beam of electrons travels in a straight line in a certain region. Can we say there is no magnetic field?
View SolutionA charge `q=4muC` has as instantaneous velociyt `v=(2hati-3hatj+hatk)xx10^6m/s` in a uniform magnetic field `B=(2hati+5hatj-3hatk)xx10^-2T`. What is the force on the charge?
View SolutionA particle initially moving towards south in a vertically downward magnetic field is deflected toward the east. What is the sign of the charge on the particle?
View SolutionAn electron experiences a magnetic force of magnitude` 4.60 xx 10^-15 N`, when moving at an angle of `60^@` with respect to a magnetic field of magnitude `3.50 xx 10^-3 T`. Find the speed of the electron.
View Solution`He^(2+)` ion travels at right angles to a magnetic field of `0.80 T` with a velocity of `10^5 m/s`. Find the magnitude of the magnetic force on the ion.
View SolutionA neutron, a proton, an electron and an alpha particle enter a region of constant magnetic field with equal velocities. The magnetic field is along the inward normal to the plane of the paper. The tracks of the particles are lebelled in Fig. The electron follow track......... and the alpha particle follow track..........

View SolutionAn electron and a proton are moving with the same kinetic energy along the same direction, When they pass through a uniform magnetic field perpendicular to the direction of their motion, they describe circular path of the same radius. Is this statement true or false?
View SolutionA charged particle enters a region of uniform magnetic field at an angle of `85^@` to the magnetic line of force. The path of the particle is a circle. Is this statement true or false?
View SolutionCan a charged particle be accelerated by a magnetic field. Can its speed be increased?
View SolutionAn electron beam projected along positive x-axis deflects along the positive y-axis. If this deflection is caused by a magnetic field, what is the direction of the field?
View SolutionAn electron and a proton are projected with same velocity perpendicular to a magnetic field.
(a) Which particle will describe the smaller circle?
(b) Which particle will have greater frequency?
View SolutionAn electron is accelerated through a `PD` of `100 V` and then enters a region where it is moving perpendiculasr to a magnetic fiedl `B=0.2T`. Find the radius of the circular path. Repeat this problem for a proton.
View SolutionA wire of length `L` carries a current `i` along the x-axis. A magnetic field `B=B_0(hati+hatj+hatk)` exists in the space. Find the magnitude of the magnetic force acting on the wire.
View SolutionA wire along the x-axis carries a current of `3.50A` in the negative direction. Calculate the force (expressed in term of unit vectors) on a `1.00cm` sectioin of the wire exerted by these magnetic fiels.
a. `B=-(0.65T)hatj b. `B=+(0.56T)hatk c. `B=-(0.31T)hatj`
d. `B=_(0.33T)hati-(0.28t)hatk` e. `B=+(0.74T)hatj-0(0.36T)hatk`
View SolutionFind net force on the equilateral loop of side `m` carrying a current of `2 A` kept in a uniform magnetic field of `2 T` as shown in figure.
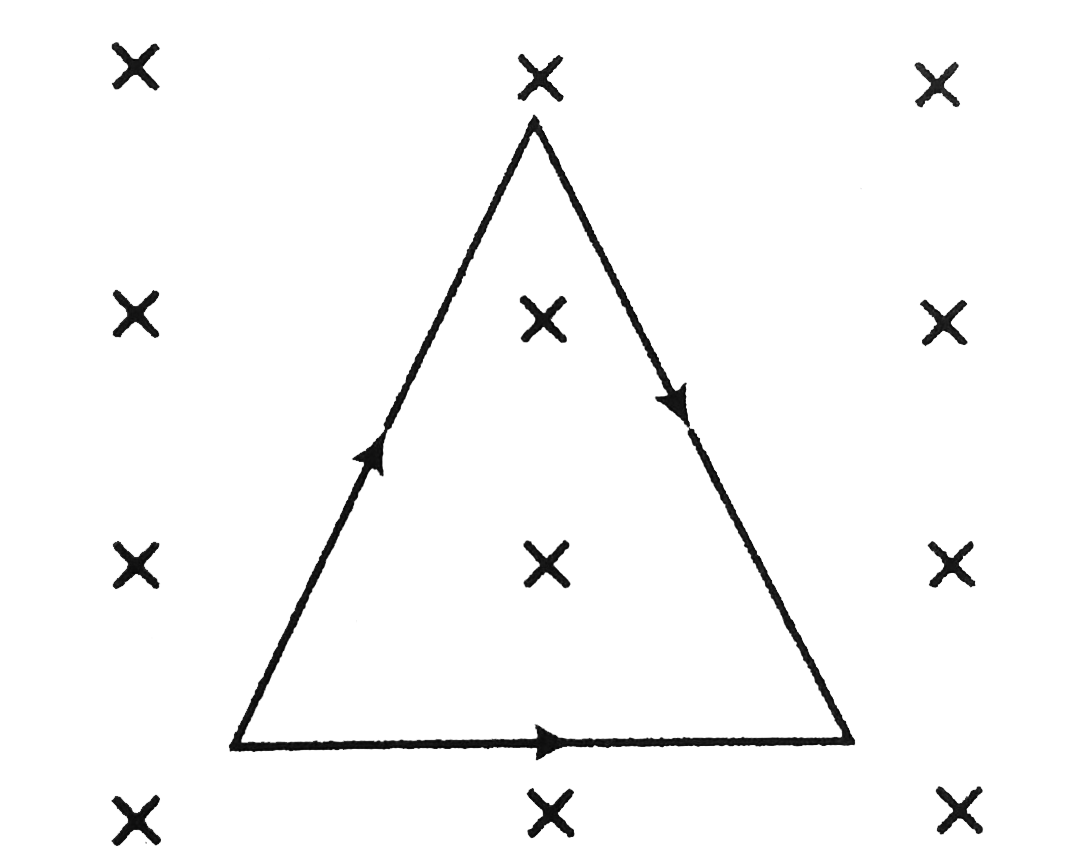
View SolutionA charge `q` is uniformly distributed on a non-conducting disc of radius `R`. It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View SolutionA circular loop of wire having a radius of `8.0 cm` carries a current of `0.20 A`. A vector of unit length and parallel to the dipole moment W of the loop is given by `0.60 hati-0.80 hatj` . if the loop located in uniform magnetic field given by `B= (0.25 T)hati+ (0.30 T)hatk` find,
(a) the torque on the loop and
(b) the magnetic potential energy of the loop.
View SolutionA length `L` of wire carries a current `i`. Show that if the wire is formed into a circular coil, then the maximum torque in a given magnetic field is developed when the coil has one turn only, and that maximum torque has the magnitude `tau=L^2iB/4pi`
View SolutionA coil with magnetic moment `1.45 A -m^2` is oriented initially with its magnetic moment antiparallel to a uniform `0.835 T` magnetic field. What is the change in potential energy of the coil when it is rotated `180^@` so that its magnetic moment is parallel to the field?
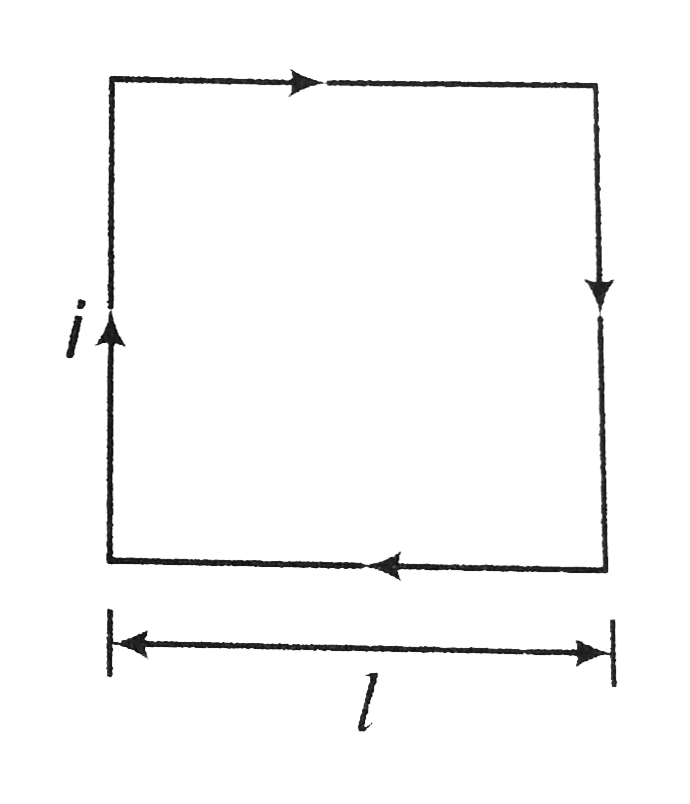
View Solutiona. A conductor in the shape of a square of edge length `l = 0.4 m` carries a current `i=10.0 A`. Calculate the magnitude and direction of magnetic field at the centre of the square.
b. If this conductor is formed into a single circular turn and carries the same current. what is the value of the magnetic field at the centre.
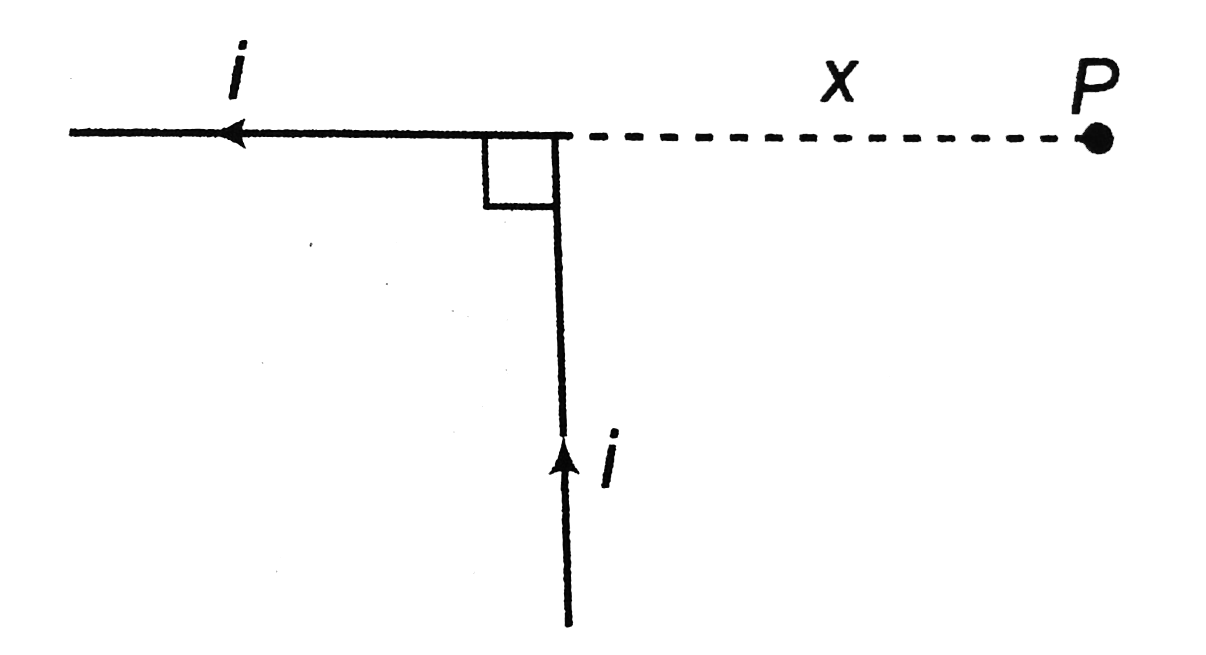
View SolutionDetermine the magnetic field at point `P` located a distance `x` from the corner of an infinitely long 2. Wire bent at right angle as shown in figure. The wire carries a steady current i.
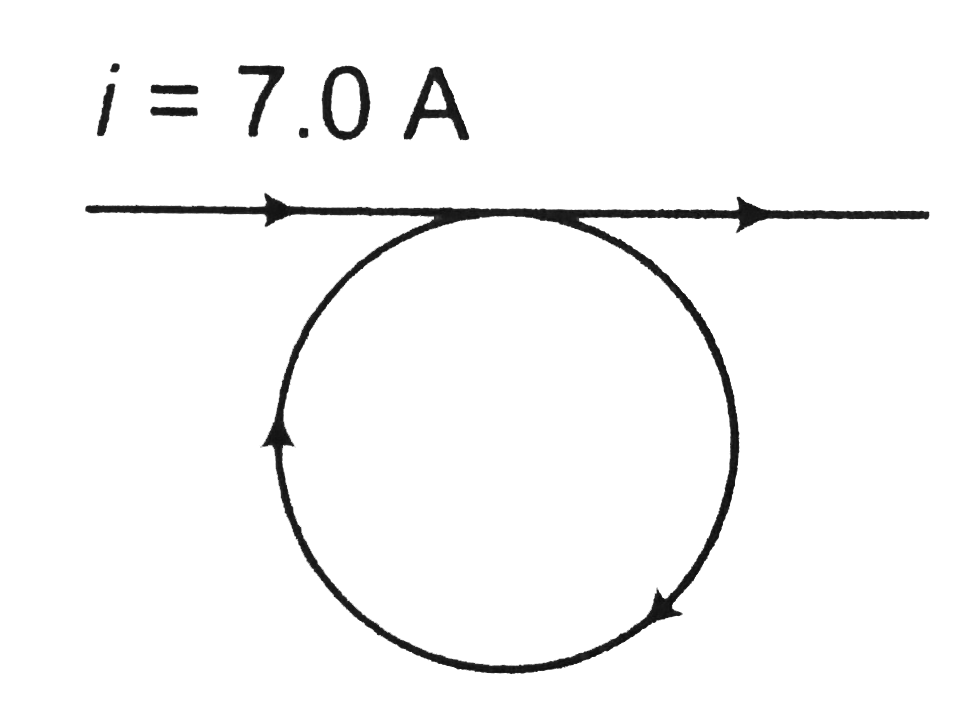
View SolutionA conductor consists of a circular loop of radius `R =10 cm` and two straight, long sections as shown in figure. The wire lies in the plane of the paper and carries a current of `i = 7.00 A` Determine the magnitude and direction of the magnetic field at the centre of the loop.
View SolutionThe segment of wire shown in figure carries a current of `i = 5.0 A` where the radius of the circular arc is `R = 3.0 cm`. Determine the magnitude and direction of the magnetic field at the origin.
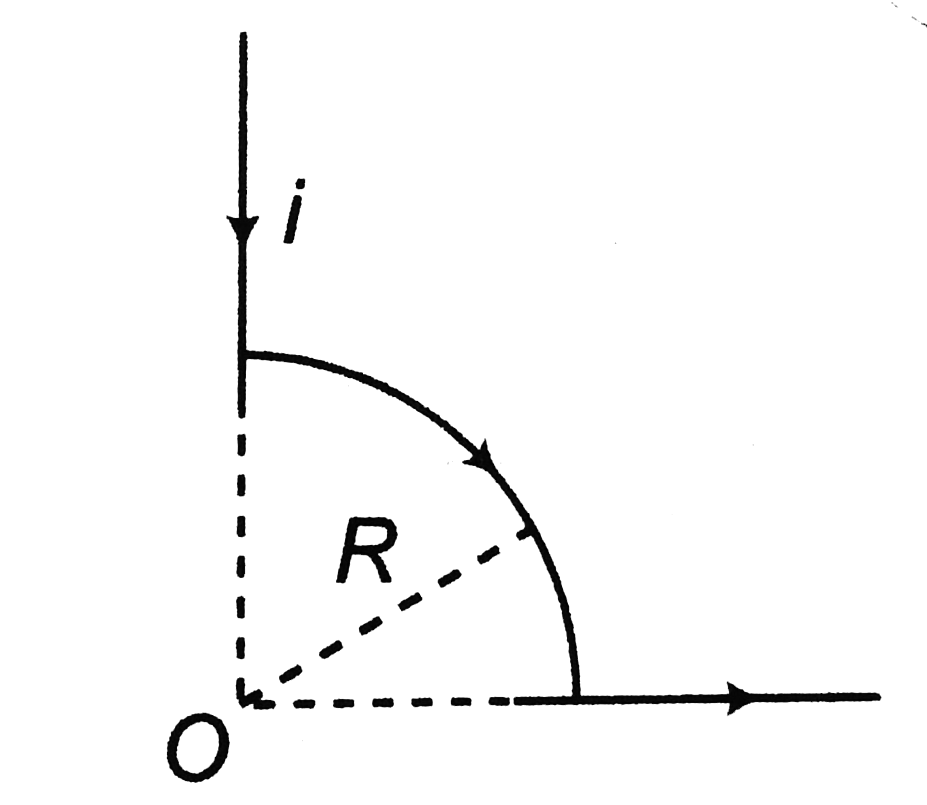
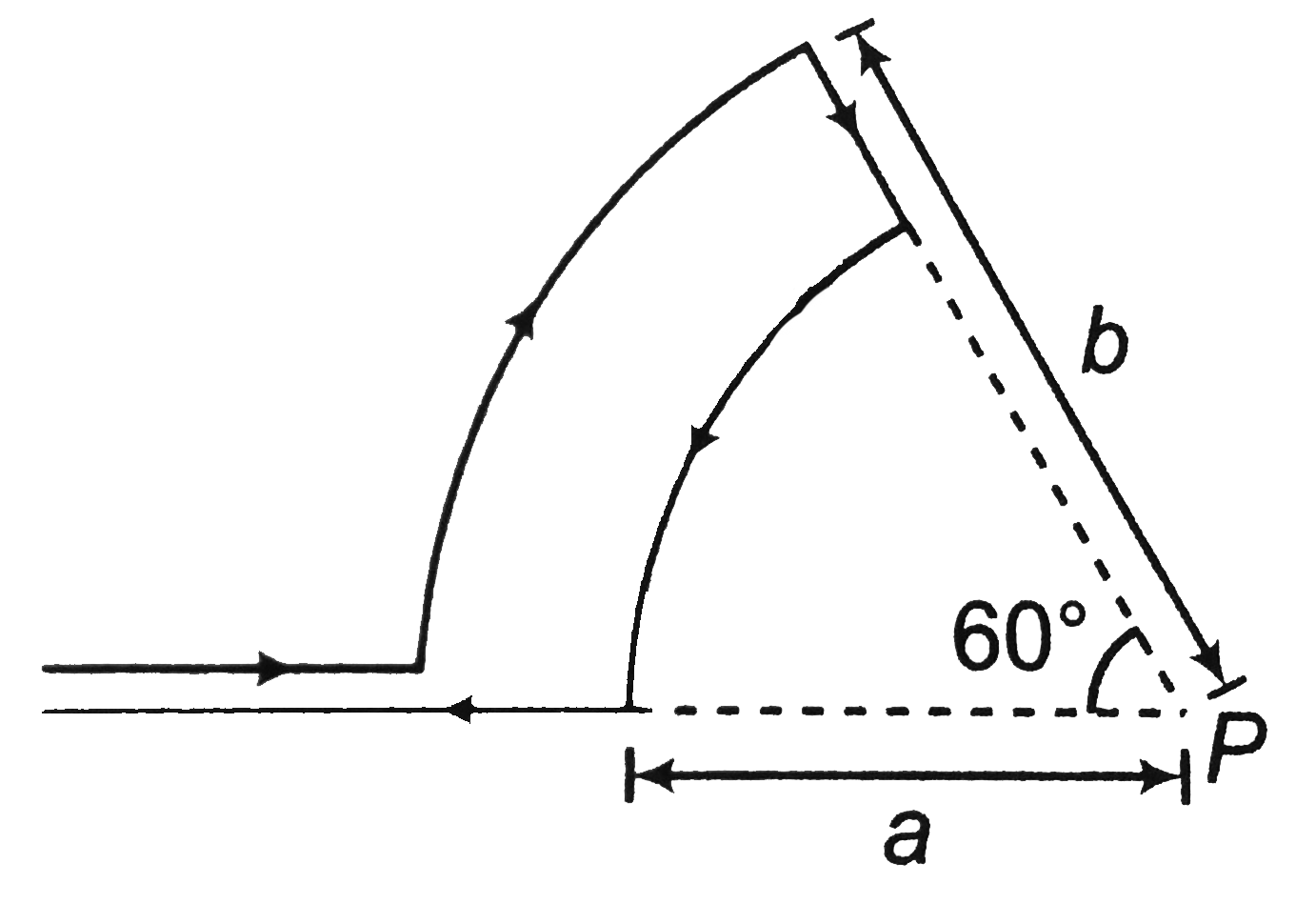
View SolutionConsider the current carrying loop shown in figure formed of radial lines and segments of circles whose centres are at point `P`. Find the magnitude and direction of B at point P.
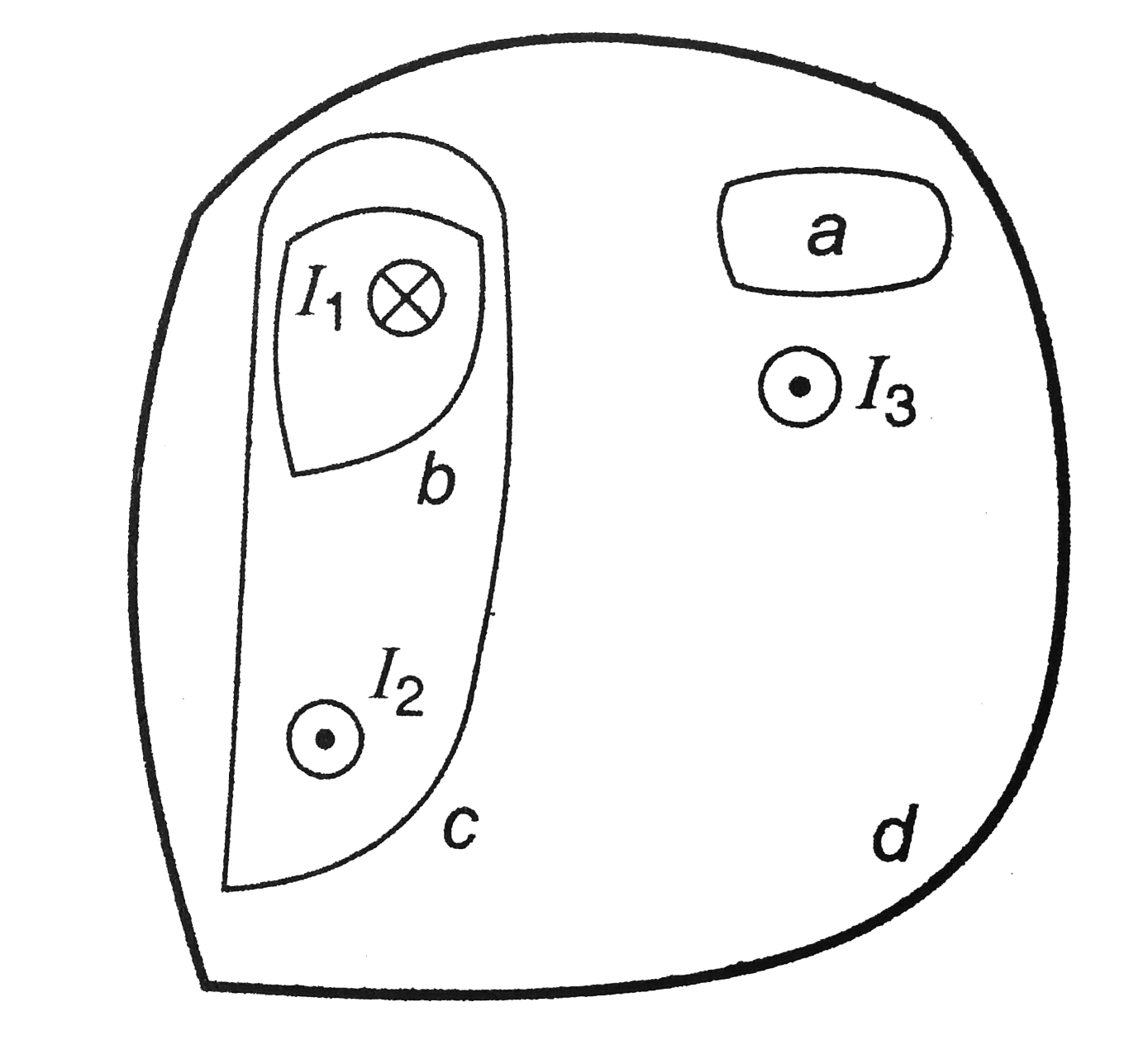
View SolutionFigure shows, in cross-section, several conductors that carry currents through the plane of the figure. The currents have the magnitudes `i_1=4.0A, I_2=6.0A`, and `I_3=2.0` A, in the directions shown. Four paths labelled a to d, are shown. What is the line integral `intB. dI` for each path? Each integral involves going around the path in the counter-clockwise direction.
View SolutionA current `i` flows along the length of an infinitely long, straight, thin-walled pipe. Then,
(a) the magnetic field at all points inside the pipe is the same, but not zero
(b) the magnetic field at any point inside the pipe is zero
(c) the magnetic field is zero only on the axis of the pipe
(d) the magnetic field is different at different points inside the pipe
View SolutionA coil al a moving Coil galvanometer twists through `90^@` when a current of one microampere is passed through it. If the area of the coil is `10^-4 m^2` and it has `100` turns, calculate the magnetic field of the magnet of the galvanometer. Given, `k = 10^-8N -m /degree.`
View SolutionA galvanometer coil `5 cm xx 2 cm` with 200 turns is suspended vertically in a field of `5 xx 10^-2 T`. The suspension fibre needs a torque of `0.125 x10^-7 N -m` to twist it through one radian. Calculate the strength of the current required to be maintained in the coil if we require a deflection of `6^@`.
View SolutionAssertion : Path of a charged particle in uniform magnetic field cannot be a parabola.
Reason : For parabolic path acceleration should be constant.
View SolutionAssertion : A beam of protons is moving towards east in vertically upward magnetic field. Then, this beam will deflect towards south.
Reason : A constant magnetic force will act on the proton beam.
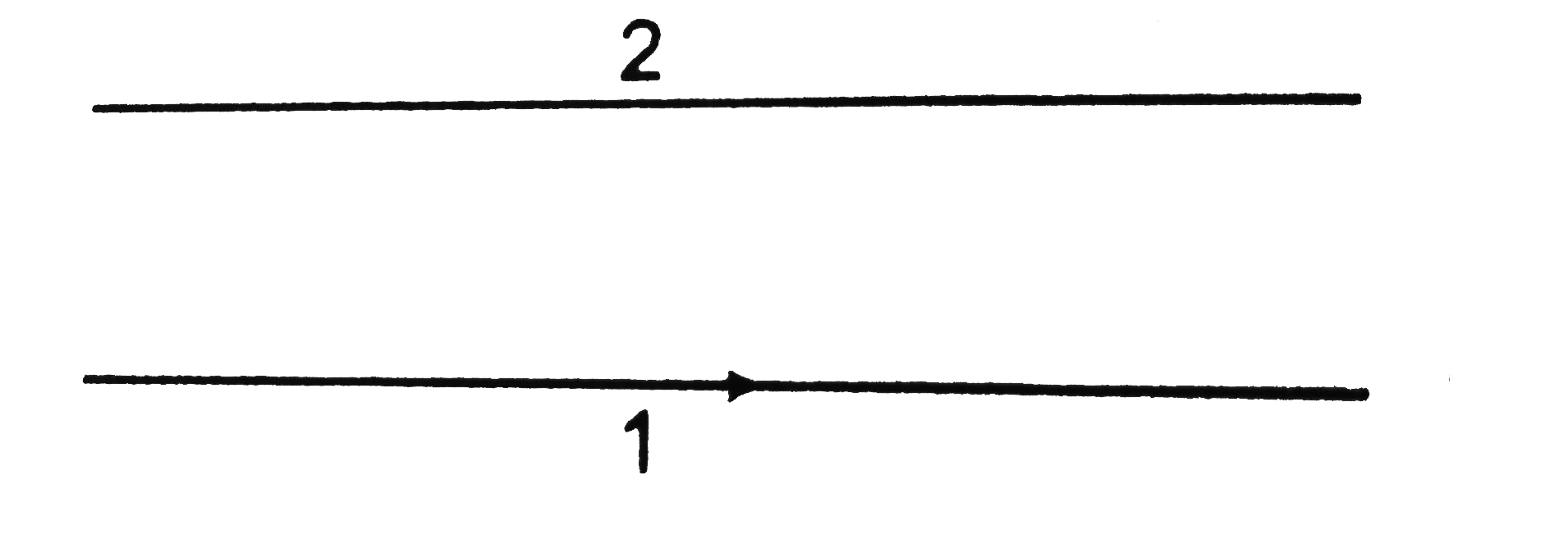
View SolutionAssertion : Current in wire-1 is in the direction as shown in figure. The bottom wire is fixed. To keep the upper wire stationary, current in it should be in opposite direction.
Reason : Under the above condition, equilibrium of upper wire is stable.
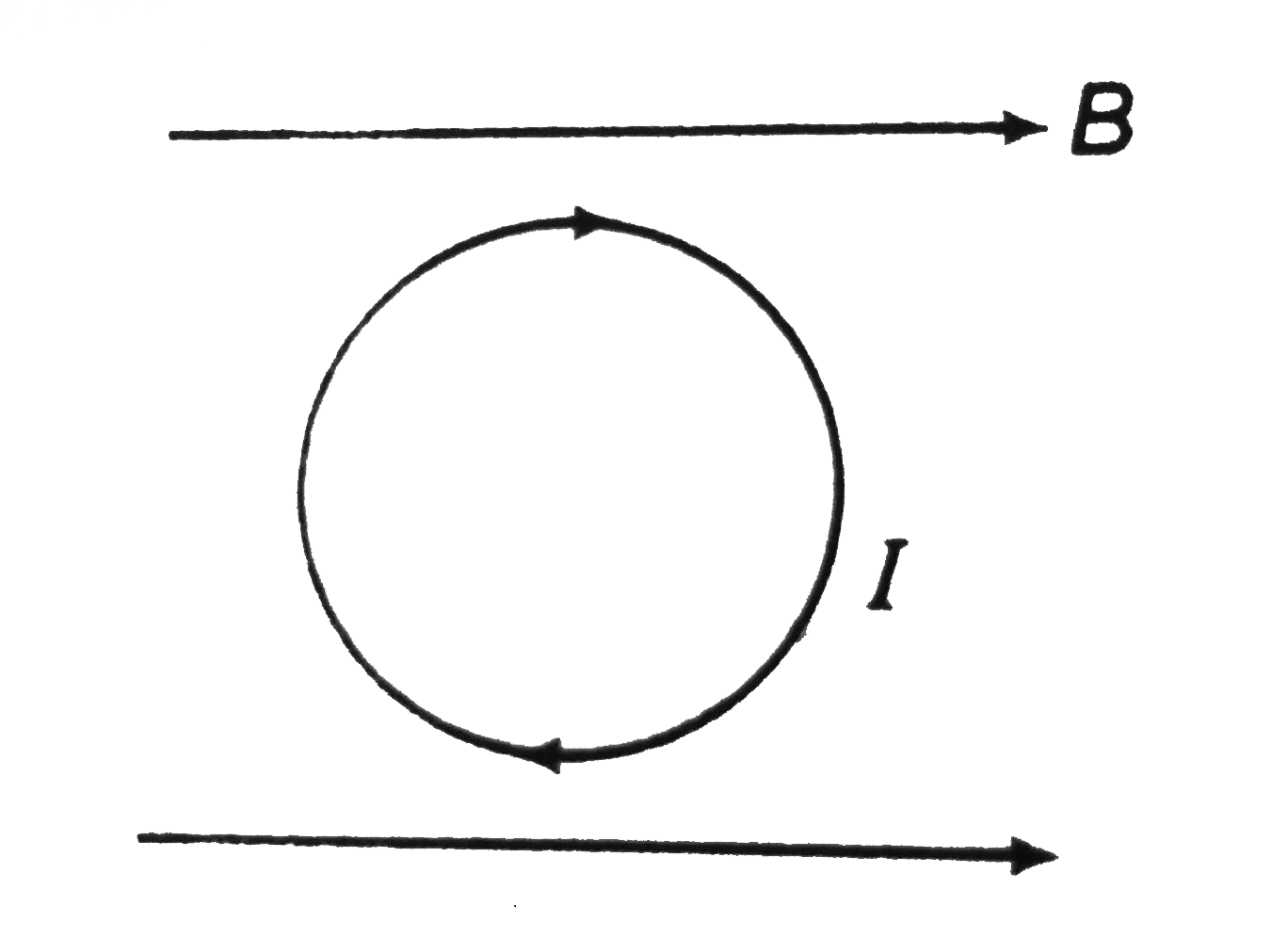
View SolutionAssertion : A current carrying loop is placed in uniform magnetic field as shown in figure. Torque in the loop in this case is zero.
Reason : Magnetic moment vector of the loop is perpendicular to paper inwards.
View SolutionAssertion : Force on current carrying loop shown in figure in `Y` magnetic field, `B = (B_0x)hatk` is along positive x-axis. Here, Be is a positive constant.
Reason : A torque will also act on the loop. brgt
View SolutionAssertion : An electron and a proton are accelerated by same potential difference and then enter in uniform transverse magnetic field. The radii of the two will be different.
Reason : Charges on them are different.
View SolutionA charged particle moves along positive y-axis with constant velocity in uniform electric and magnetic fields. Ilf magnetic fiedl is actig along positive x-axis, then, electric field should act along positive z-axis.
Reason: To keep the charged particle undeviated the relation `E=Bxxv` must hold good.
View SolutionAssertion: Power of a magetic force on a charged particle is always zero.
Reason: Power of electric force on charged particle cannnot be zero.
View SolutionAssertion : If a charged particle enters from outside at right anglels in uniform magnetic field. The maximum time spent in magnetic field may be `(pim)/(Bq)`.
Reasong: It can complete only semi circle in the magnetic field.
View SolutionAssertion: A charged particle enters in a magnetic field `B=B_0hati with velocity v=v_0hati+v_0hatj, ` then minimum speed of charged particle may be `v_0`.
Reason: A variable acceleration particle may be `v_0`.
View SolutionAssertion: A charged particle is moving in a circle with constant speed in uniform magnetic field. If we increase the speed of particle to twice, its acceleration will become four times.
Reason: In circular path of radius `R` with constant speed `v`, acceleration is given by `v^2/R`
View SolutionThe universal proporty among all substance is
View SolutionA charged particle moves in a circular path in a uniform magnetic field. If its speed is reduced, then its tiem period will
View SolutionA straight wilre of diameter `0.5 mm` carrying a current `2A` is replaced by another wire of diameter `1 mm` carrying the same current. The strength of magnetic field at a distance `2 m` away from the centre is
View SolutionThe path of a charged particle moving in a uniform steady magnetic field cannot be a
View SolutionThe `SI` unit of magnetic permebility is
View SolutionIdentify the correct statement bout the magnetic field lines.
View SolutionIdentify the correct sttement related to the direction of magnetic moment of a planar loop.
View SolutionA non planar closed loop of arbitrary shape carryign a current I is placed in uniform magnetic field. The force acting on the loop
View SolutionThe magnetic dipole moment of current loop is independent of
View SolutionThe accelertion of a electron at a certain moment in a magnetic field `B=2hati+3hatj+4hatk` is `a=xhati+hatj-hatk`. The value of `x` is
View SolutionA closed loop a current `I` lies in the xz-plane. The loop will experience a force if it is placed in a region occupied by uniform magnetic field along
View SolutionA stream of protons and `alpha`-particle of equal momenta enter a unifom magnetic field perpendicularly. The radii of their orbits are in the ratio
View SolutionAs loop of magnetic moment `M` is placed in the orientation of unstable equilbirum position in a uniform magnetic field `B`. The external work done in rotating it through an angle `theta` is
View SolutionA current of `50 A` is placed through a straight wire of length `6 cm` then the magnetic induction at a point `5cm` from the either end of the wire is (`1gauss=10^-4T`)
View SolutionThe magnetic field due to a current carrying circular loop of radius `3 m` at as point on the axis at a distance of `4m` from the centre is `54 muT`. What will be its value at the centre of the loop.
View SolutionA conductor `ab` of arbitrary shape carries current I flowing from `b` to `a`. The length vector `ab` is oriented from `a` to `b`. The force `F` experienced by this conductor in as uniform magnetic field B is
View SolutionWhen an electron is accelerated through a potential difference `V`, it experience a force `F` through as uniform transverse magnetic field. If the potential difference is increased to `2 V,` the force experoenced by the electron in the same magnetic field is
View SolutionTwo long straight wires, each carrying a current `I` in opposite directions are separated by a distance `R`. The magnetic induction at a point mid way between the wire is
View SolutionThe magnetic field ast a distance `x` on the axis of a circular coil of radius `R` is `1/8` th of that at the centre. The value of x is
View SolutionElectric field and magnetic field `n` a region of space is given by `E=E_0hatj` and `B=B_0hatj`. A particle of specific charge alpha is released from origin with velocity `v=v_0hati`. Then path of particle
View SolutionAn electron having kinetic energy `K` is moving i a circular orbit of radius `R` perpendicular to a uniform magnetic induction. If kinetic energy is douled and magnetic induction tripled, the radius will become
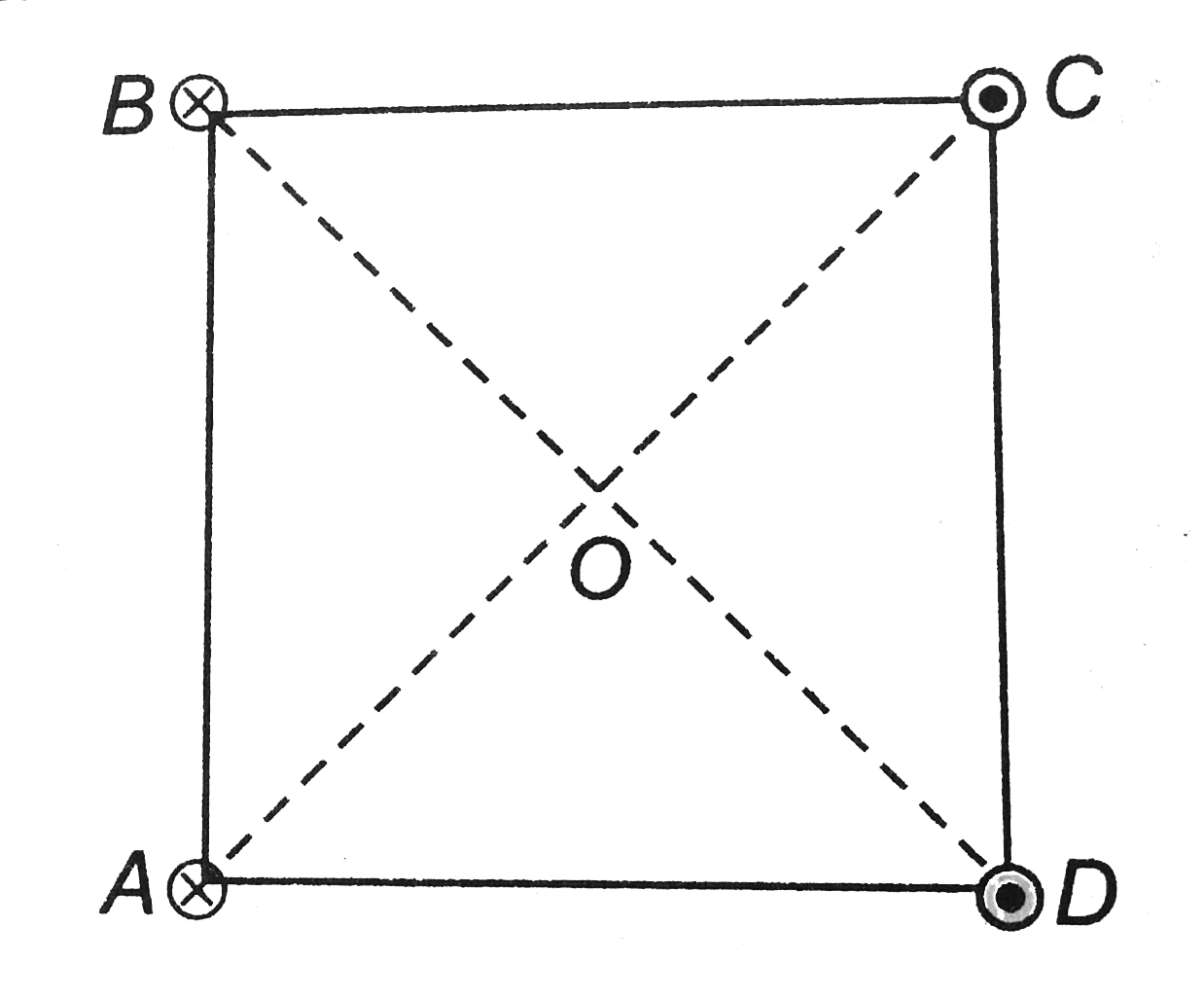
View SolutionFour long staight wires are located at the corners of a square `ABCD`. All the wires carry equal currents. Current in the wires `A` and `B` are inwards and in `C` and `D` are outwards. The magnetic field at the centre `O` is along
View SolutionA charged particle of mass `m` and charge `q` is accelerated through a potential differences of `V` volts. It enters of uniform magnetic field `B` which is directed perpendicular to the direction of motion of the particle. The particle will move on a circular path of radius
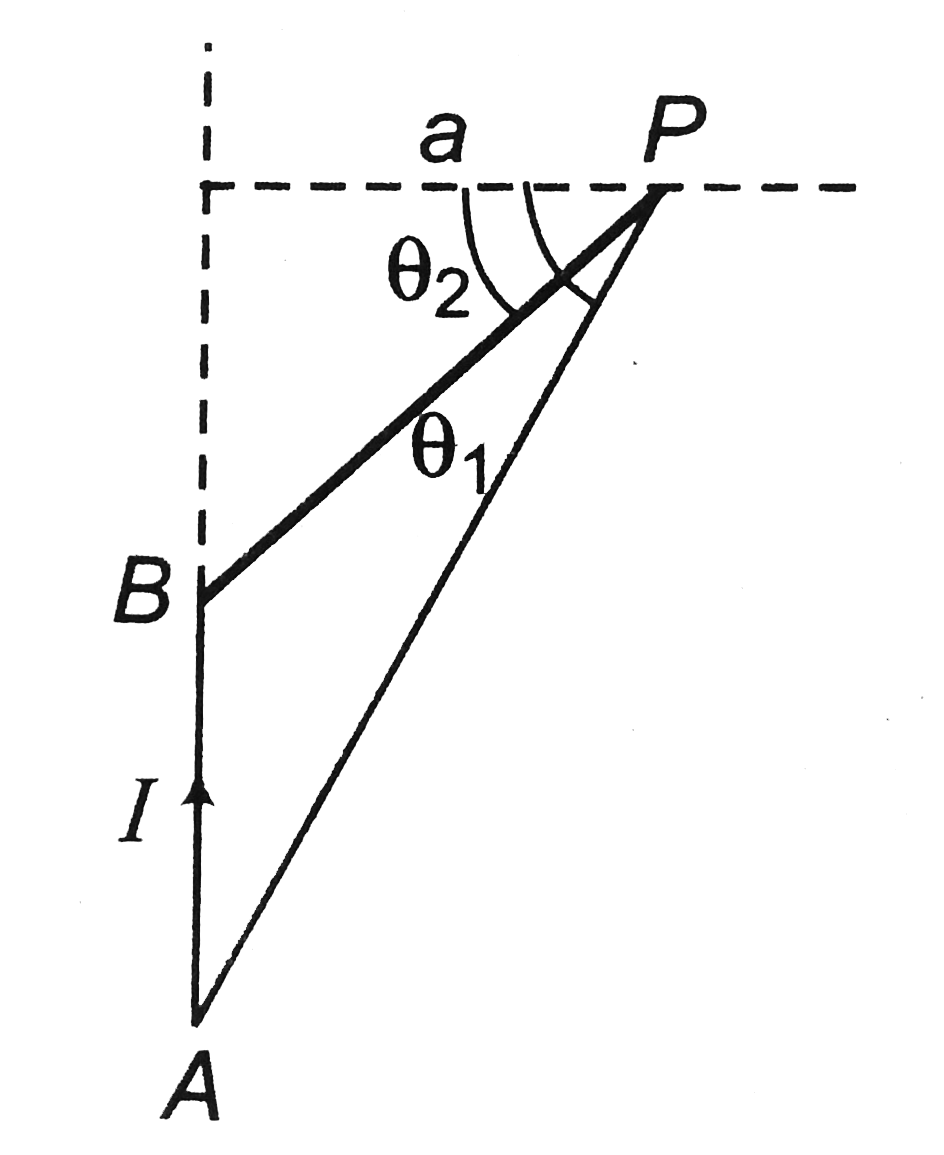
View SolutionThe straight wire `AB` carries a current `I`. The ends of the wire subtend angles `theta_1` and `theta_2` at the point `P` as shown in figure. The magnetic field at the point `P` is
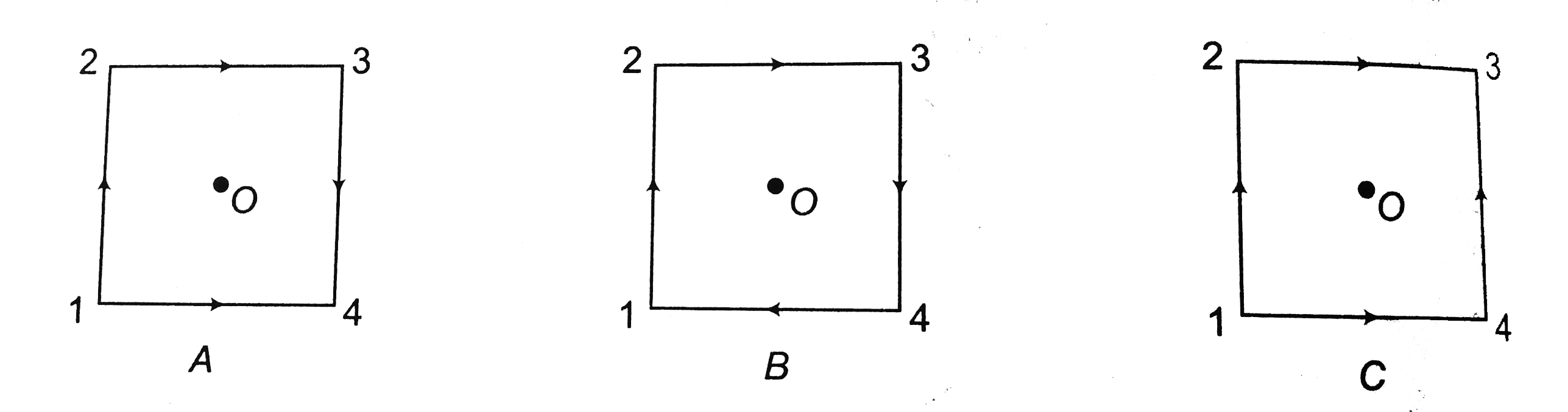
View SolutionThe figure shows three indentical current carryng square loops `A, B` and `C`. Identify the correct statement related to magnetic field B at the centre `O` of the square loop. Current in each wire is I.
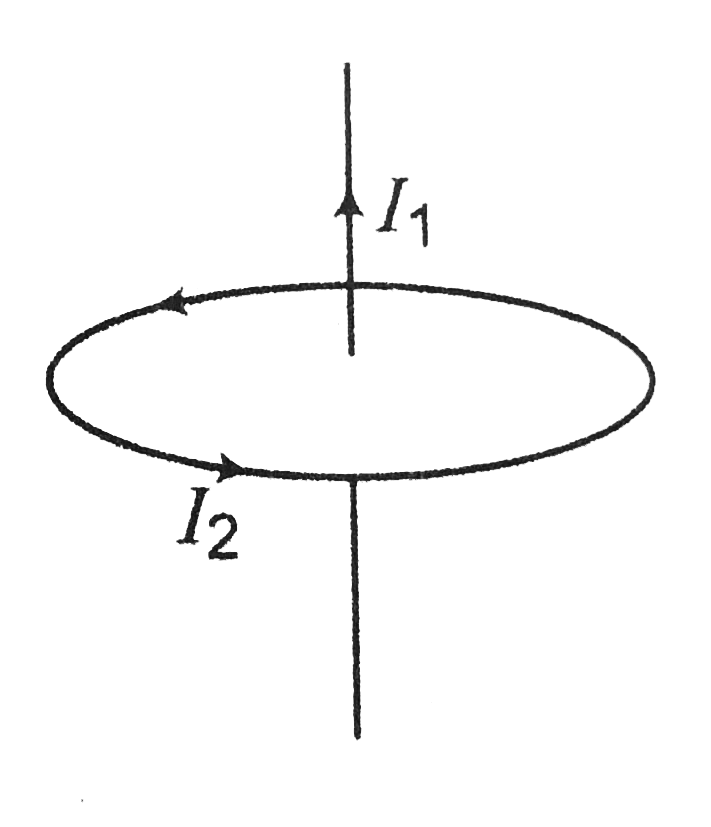
View SolutionThe figure shows a long straigh wire carryhing a current `I_1` along the axis of a circular ring carrying a current I_2`. Identify the correct statement.
View SolutionThe figure shows a wire frame in xy-plane carryigna current `I`. The magnetic field at the point `O` is
View SolutionAn electron moving in a circular orbit of radius `R` with frequency `f`. The magnetic field at the centre of the orbit is
View SolutionA square loop of side a carris a current `I`. The magnetic field at the centre of the loop is
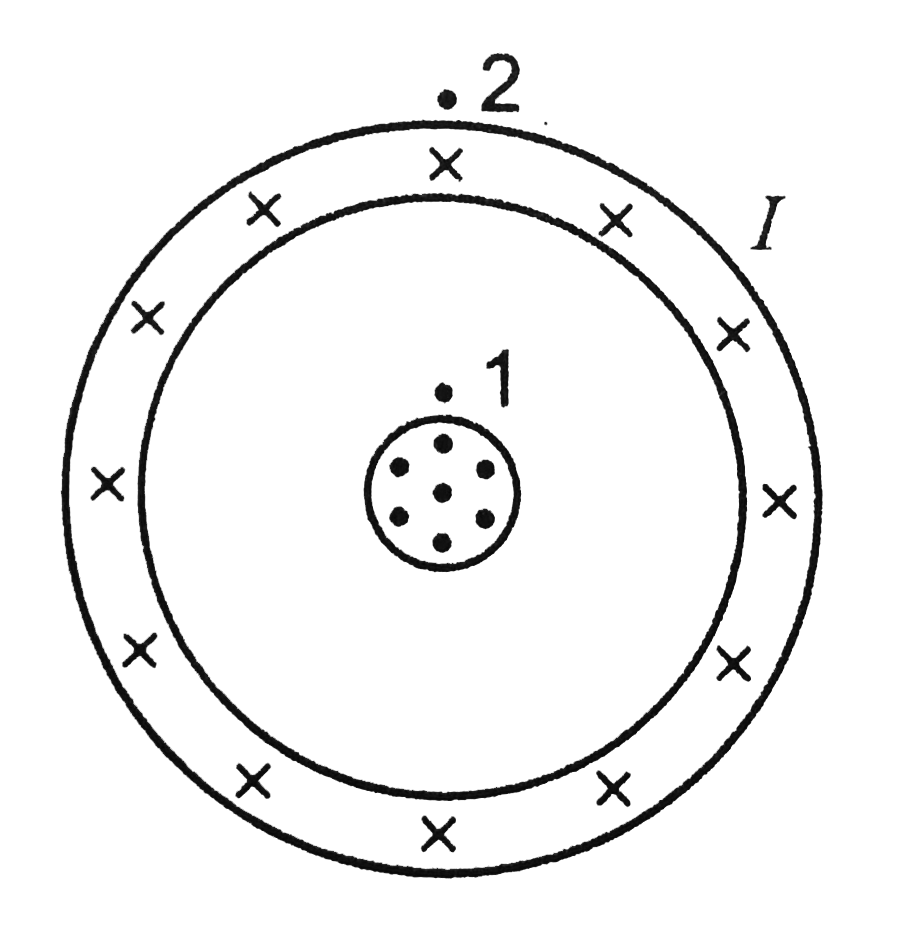
View SolutionThe figure shows the cross section of two long coaxial tubes carrying equal current `I` in opposites directions. If `B_1` and `B_2` are magnetic fields at point 1 and 2 as shown in figure then
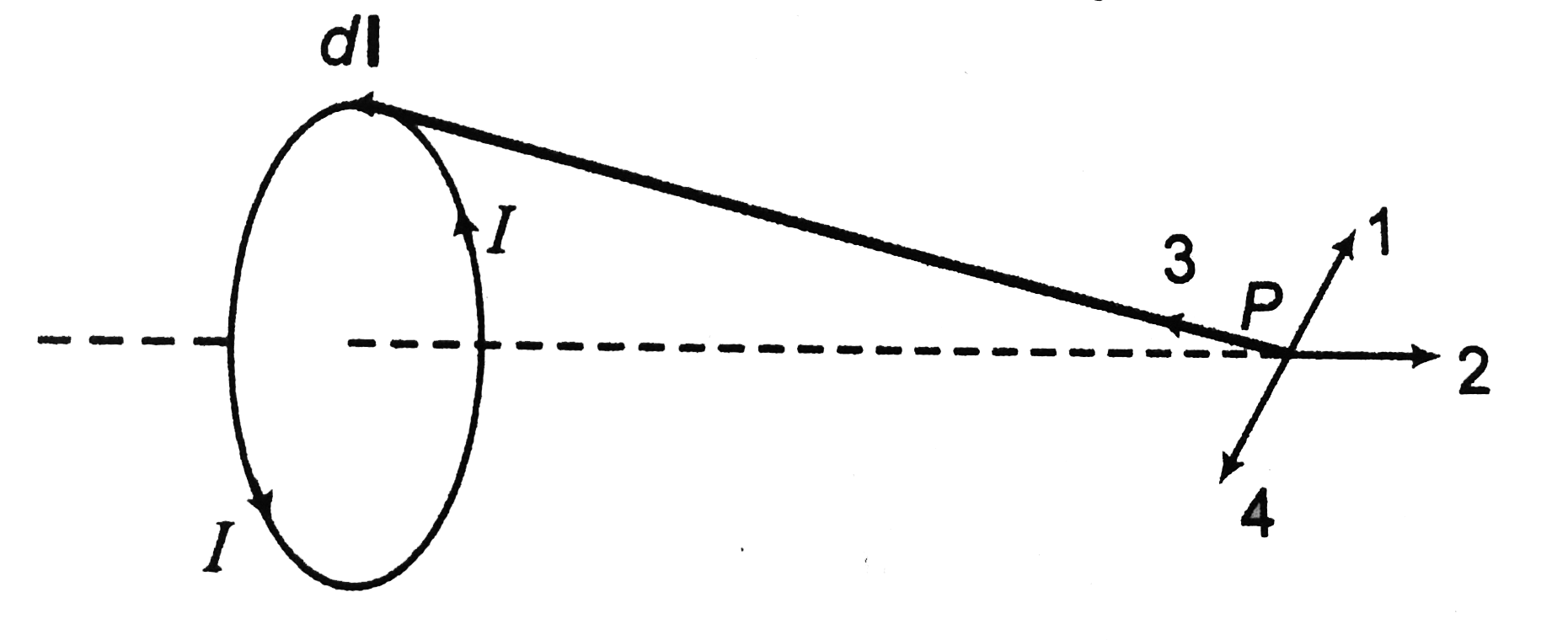
View SolutionThe figure shows a point `PO` on the axis of a circular loop carrying current `I`. The correct direction of magnetic field vector at `P` due to `dI` is respectively by
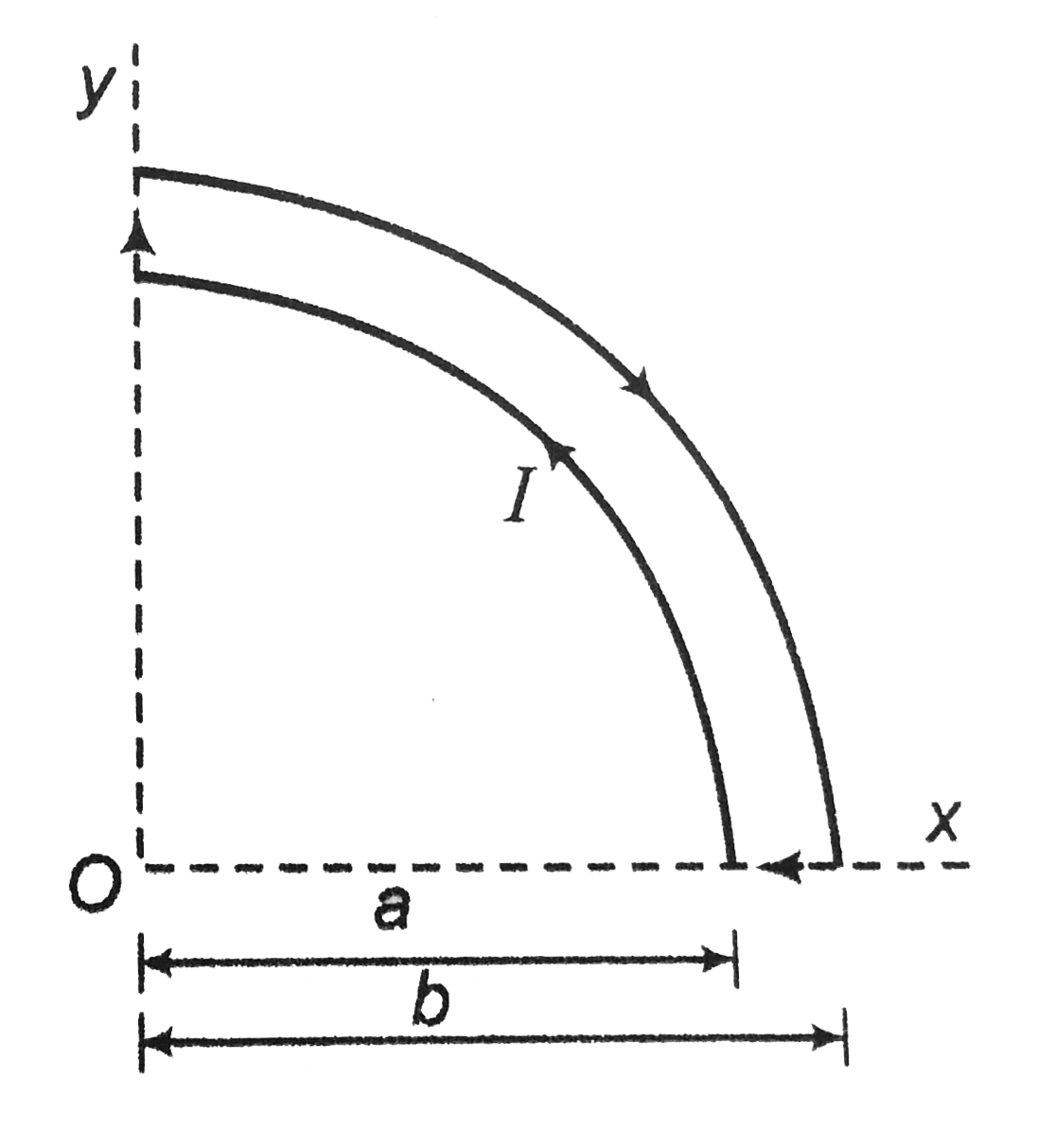
View SolutionIn the figure, the curved part represents arc of a circle of radius `x`. If it carries a current `I` then the magnetic field at the point `O` is
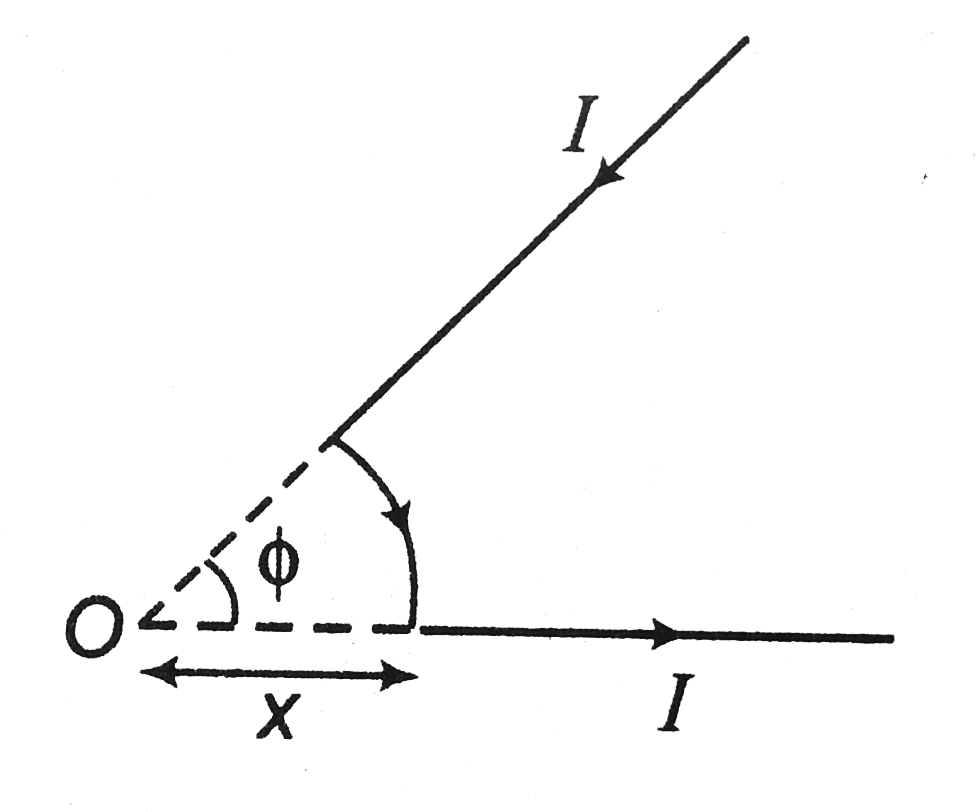
View SolutionA cylindrical long wire of radius `R` carries a current `I` uniformly distributed over the cross sectional area of the wire. The magnetic field at a distance `x` from the surface inside the wire is
View SolutionA circular loop carrying a current `I` is placed in the xy-plane as shown in figure. A uniform magnetic fied `B` is oriented along the positive z-axis. The loop tends to
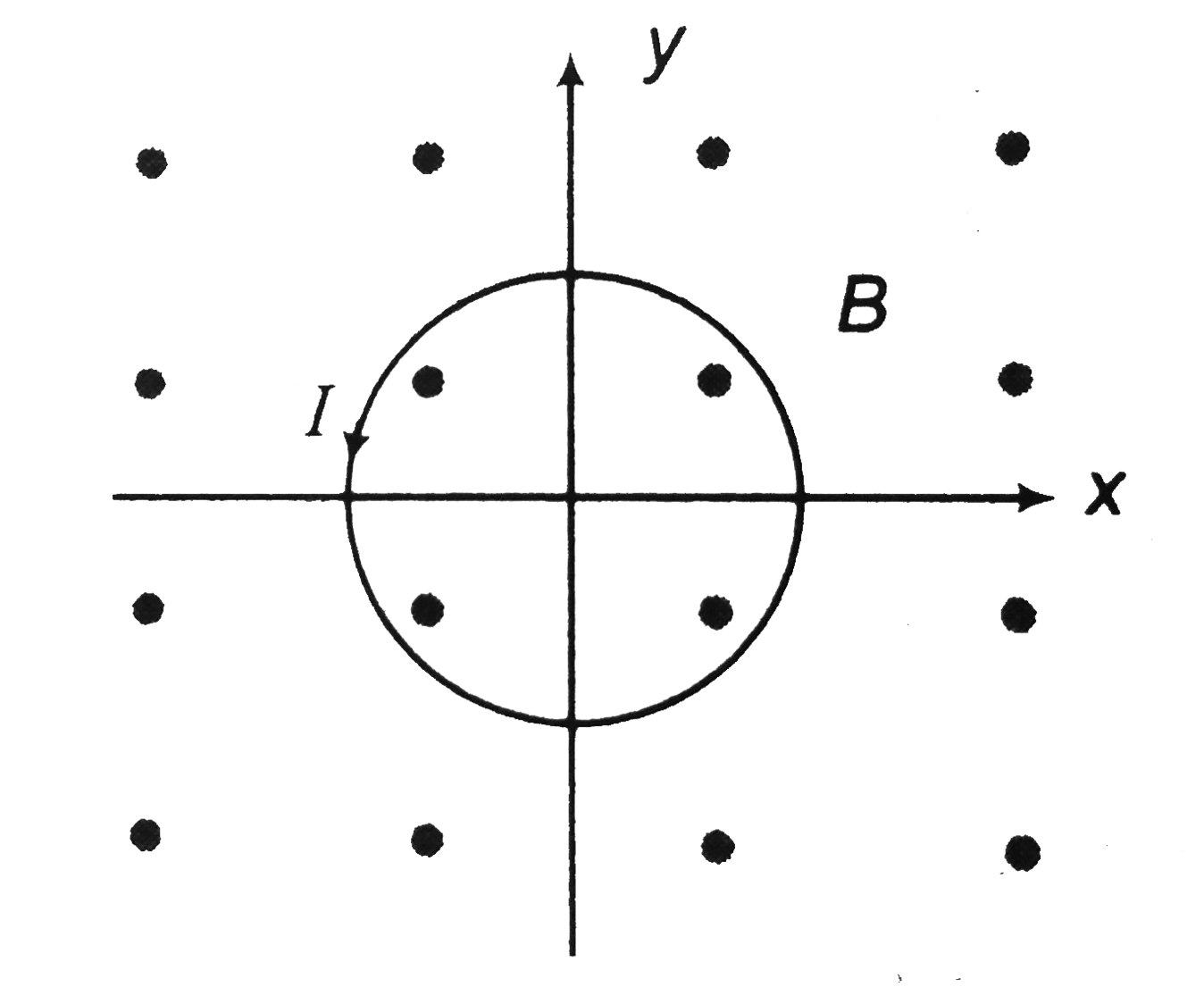
View SolutionAn electron has velocity `v = (2.0 xx 10^6 m/s) hati + (3.0 x 10^6 m/s )hatj`. Magnetic field present in the region is `B = (0.030 T) hati - (0.15 T) hatj`.
(a) Find the force on electron.
(b) Repeat your calculation for a proton having the same velocity.
View SolutionAn electron moves through a uniform magnetic fiedl given by `B=B_xhati+(3B_x)hatj`. At a particular instant, the electron has the velocity `v=(2.0hati+4.0hatj)` m/s and the magnetic force acting on its is `(6.4xx10^-19N)hatk` Find `B_x`.
View SolutionA particle with charge `7.80 muC` is moving with velocity `v = - (3.80 xx 10^3 m/s)hatj`. The magnetic force on the particle is measured to be `F = + (7.60 xx 10^-3 N)hati - (5.20 xx 10^-3 N)hatk`
(a) Calculate the components of the magnetic field you can find from this information.
(b) Are the components of the magnetic field that are not determined by the measurement of the force? Explain.
(c) Calculate the scalar product `B .F`. What is the angle between `B` and `F`
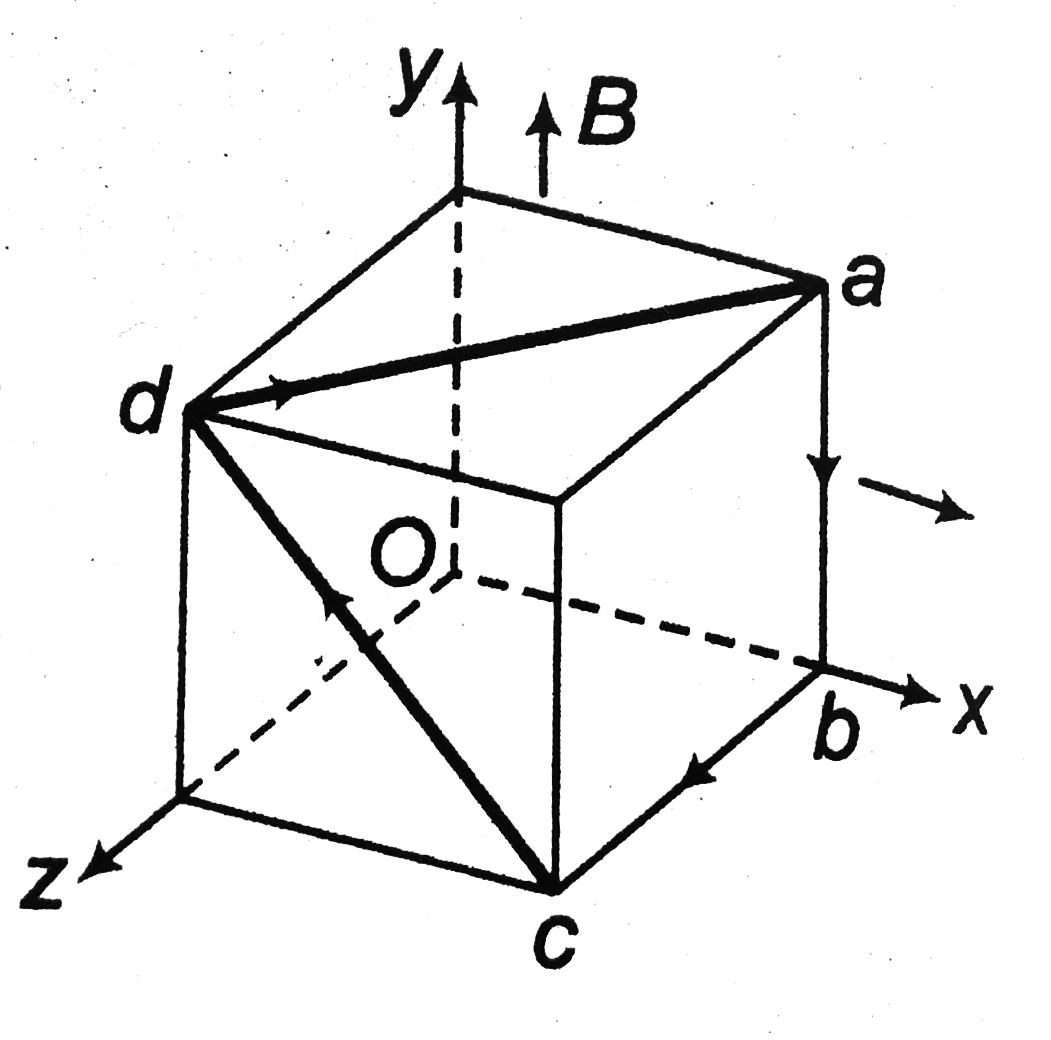
View SolutionEach of the lettered points at the corners of the cube as shown in Fig. 1.60 represents a positive charge q moving with a velocity of magnitude v in the direction indicated. The region in the figure is in a uniform magnetic field `vec B`, parallel to the x-axis and directed toward right. Copy the figure, find the magnitude and direction of the force on each charge and show the force in your diagram.

View SolutionAn electron in the beam of a TV picture tube is accelerated by a potential difference of `2.00 kV`. Then, it passes through region of transverse magnetic field, where it moves in a circular arc with radius `0.180 m`. at is the magnitude of the field?
View SolutionA deuteron (the nucleus of an isotope of hydrogen) has a mass of `3.34 xx 10^-27` kg and a charge of `+e`. The deuteron travels in a circular path with a radius of `6.96 mm` in a magnetic field with magnitude `2.50 T`.
(a) Find the speed of the deuteron.
(b) Find the time required for it to make half of a revolution.
(c) Through what potential difference would the deuteron have to be accelerated to acquire this speed?
View SolutionA neutral particle is at rest in a uniform magnetic field `B`. At time `t = 0` it decays into two charged particles, each of mass `m`.
(a) If the charge of one of the particles is `+q`, what is the charge of the other?
(b) The two particles move off in separate paths, both of them lie in the plane perpendicular to `B`. At a later time, the particles collide. Express the time from decay until collision in terms of `m, B` and `q`.
View SolutionAn electron at point `A` in figure has a speed `v_0 = 1.41 xx 10^6 m/s`. Find

(a) the magnitude and direction of the magnetic field that will cause the electron to follow the semicircular path from `A` to `B`,
(b) the time required for the electron to move from `A` to `B`.
View SolutionA proton of charge `e` and mass `m` enters a uniform magnetic field `B = Bi` with an initial velocity `v=v_xhati+v_yhatj`. Find an expression in unit vector notation for its velocity at time `t`.
View SolutionA proton moves at a constant velocity of `50 m/s` along the x-axis, in uniform electric and magnetic fields. The magnetic field is `B = (2.0 mT)hatj`. What is the electric field?
View SolutionA particle having mass m and charge `q` is released from the origin in a region in which ele field and magnetic field are given by `B=-B_0hatj`and `E=E_0hatk`.
Find the y- component of the velocity and the speed of the particle as a function of it z-coordinate.
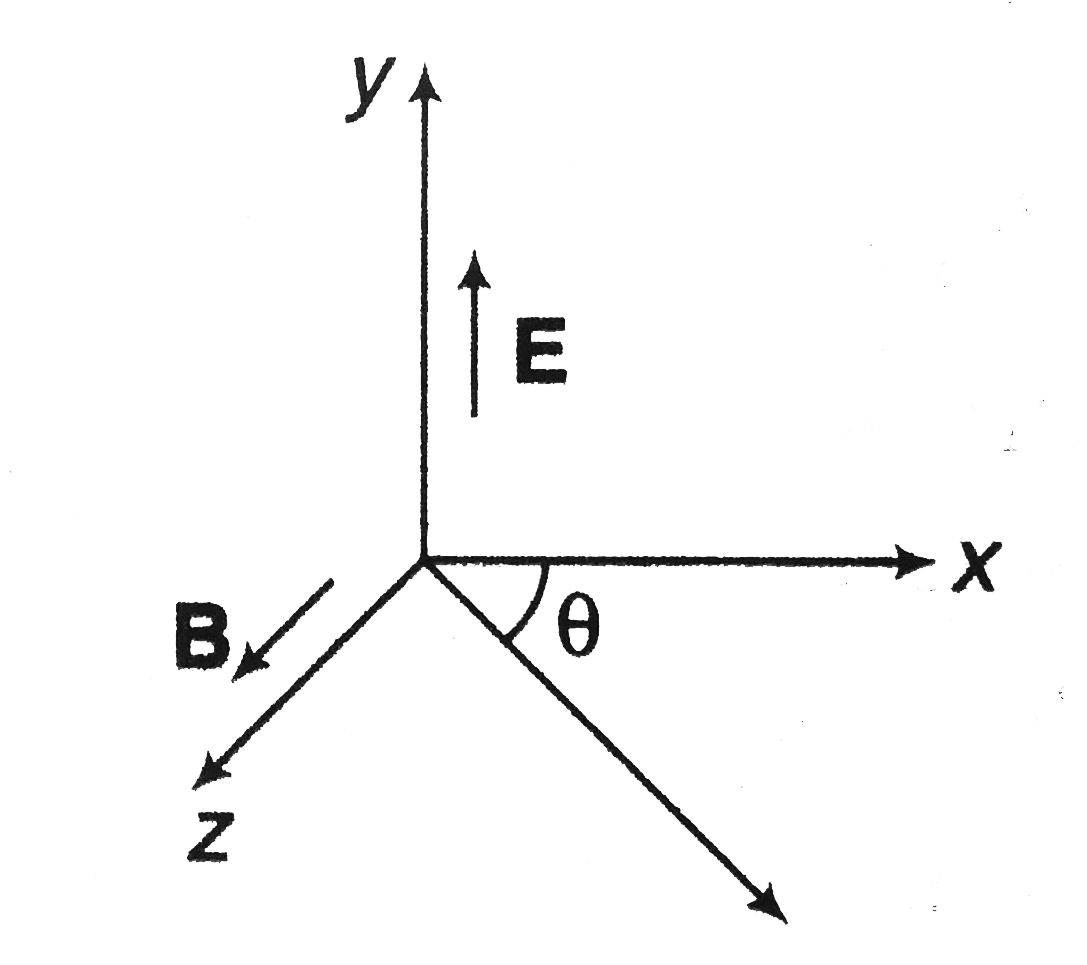
View SolutionProtons move rectilinearly in the region of space where there are uniform mutually perpendicular electric and magnetic fields `E` and `B`. The trajectory of protons lies in the plane xz as shown in the figure and forms an angle 9 with x-axis. Find the pitch of the helical trajectory along which the protons will move after the electric field is switched off.
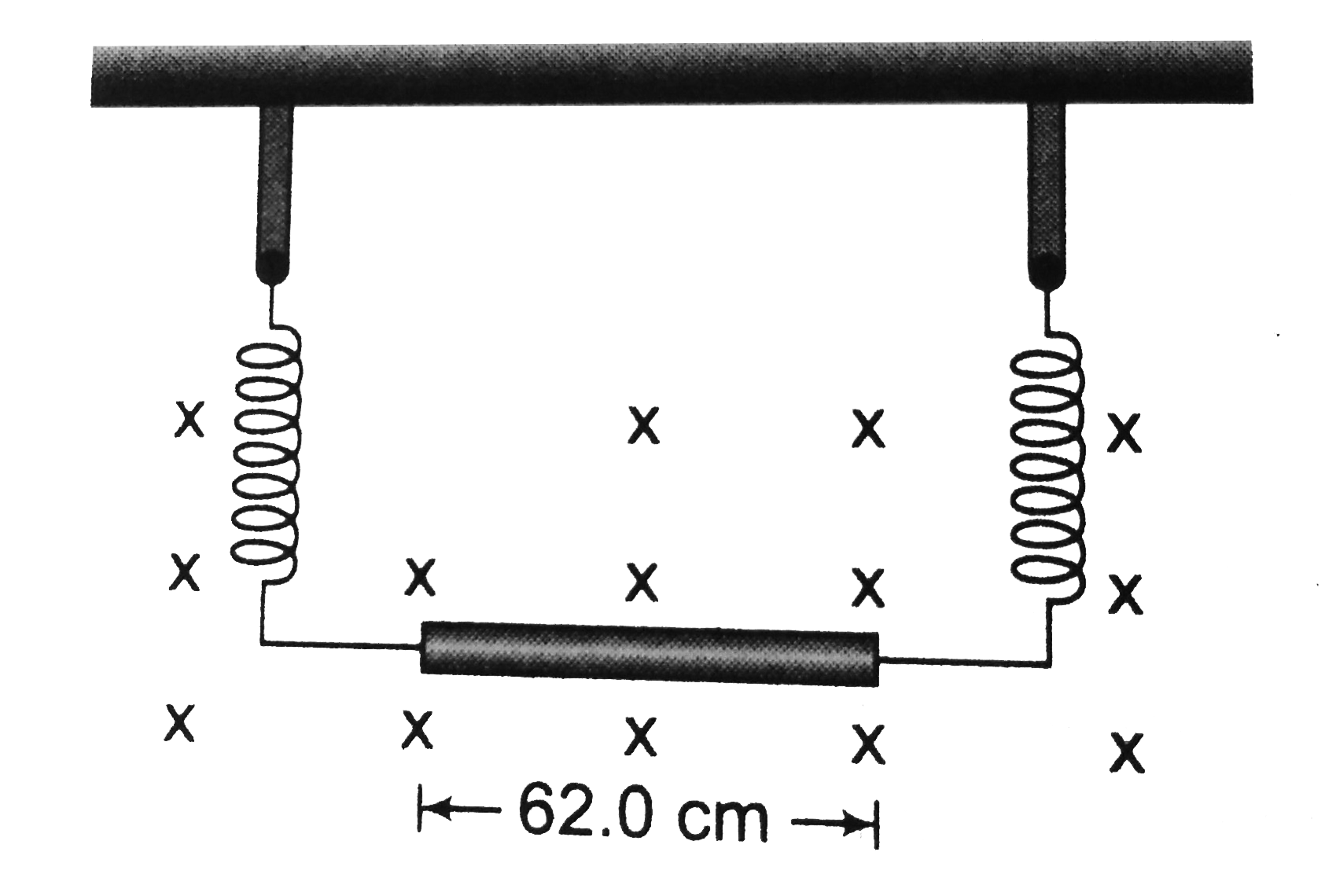
View SolutionA wire of `62.0 cm` length and `13.0 g` mass is suspended by a pair of flexible leads in a uniform magnetic field of magnitude `0.440 T` in figure. What are the magnitude and direction of the current required to remove the tension in the supporting leads? Take `g = 10 m/s^2`
View SolutionA thin, `50.0 cm` long metal bar with mass `750 g` rests on, but is not attached to, two metal supports in a `0.950 T` magnetic field as shown in figure. A battery and a resistance `R = 25.0Omega` in series are connected to the supports.
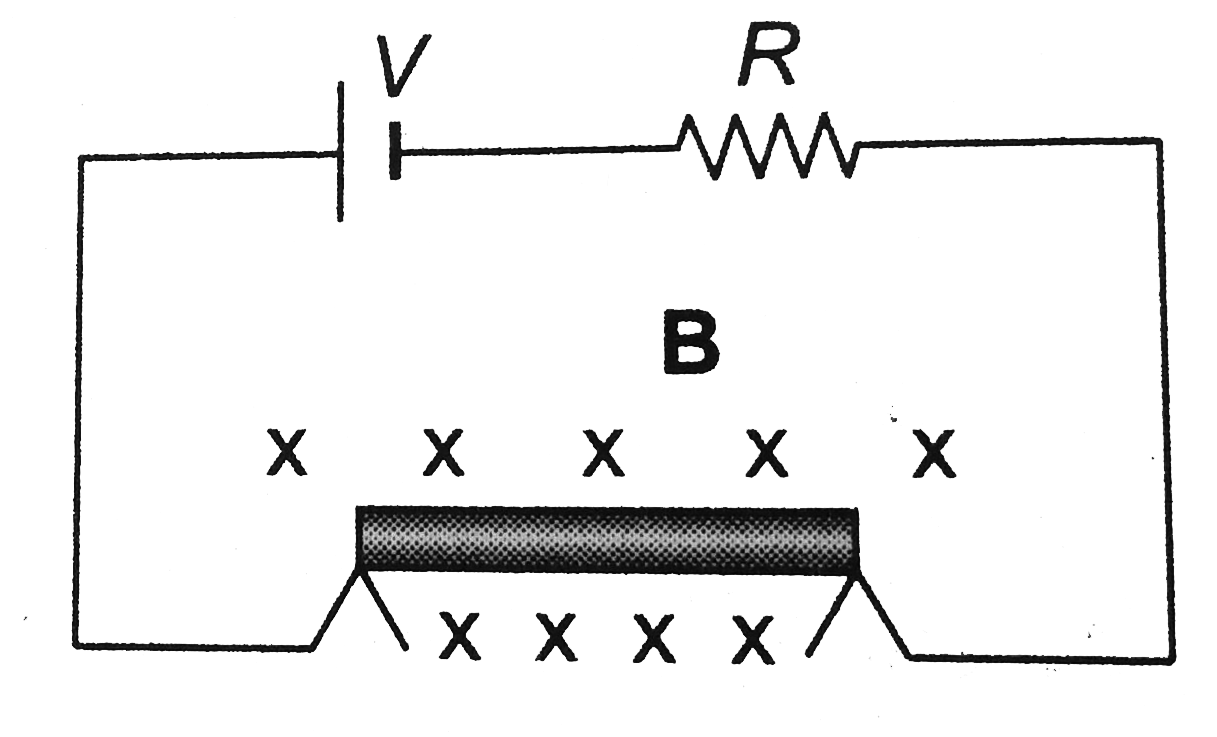
(a) What is the largest voltage the battery can have without breaking the circuit at the supper
(b) The battery voltage has this maximum value calculated. Decreasing the resistance to `2.0 Omega` the initial acceleration of the bar.
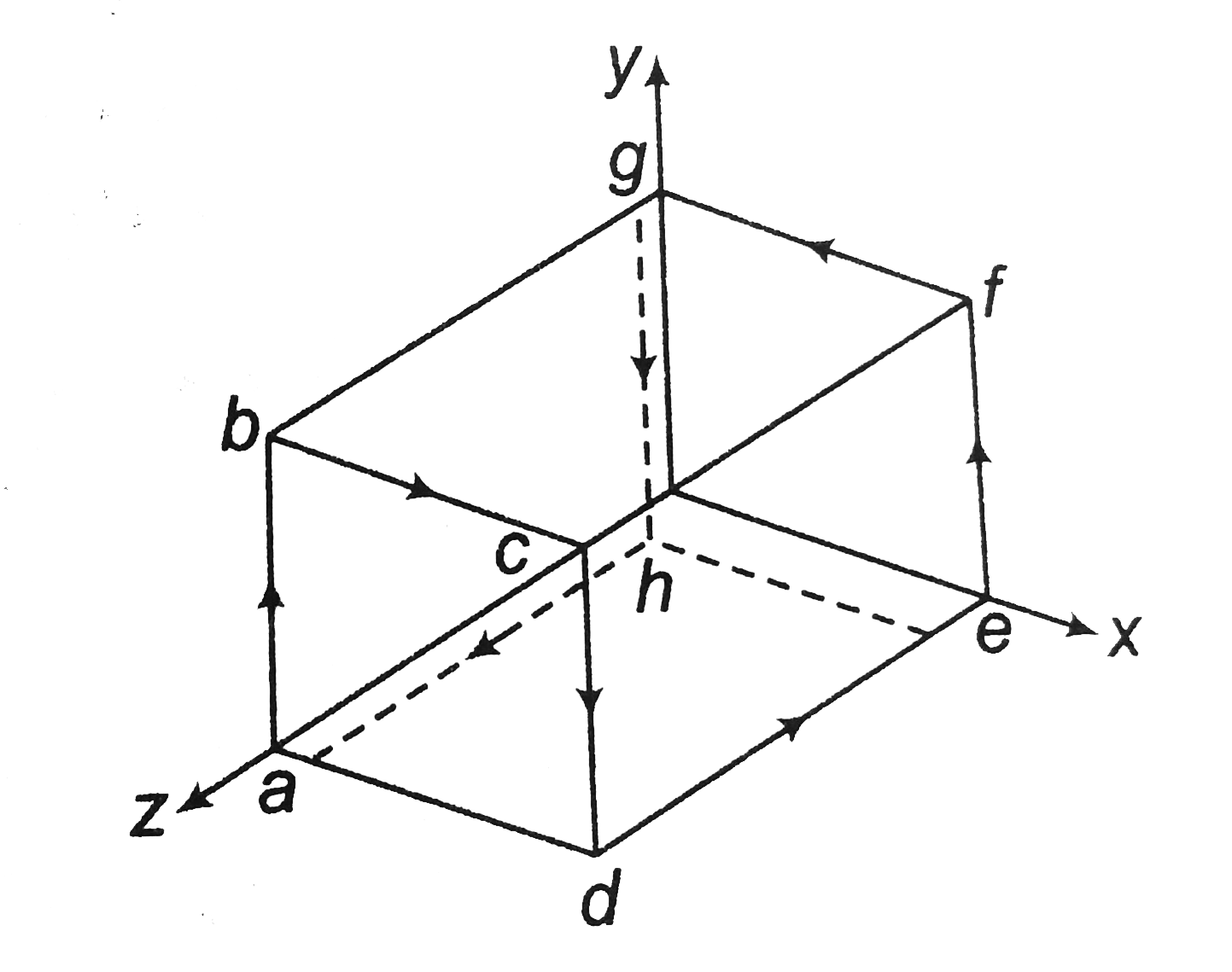
View SolutionIn figure, the cube is `40.0 cm` on each edge. Four straight segments of wire `ab, bc, cd` and `da` form a closed loop that carries a current `I=5.00A`, in the direction shown. A uniform magnetic field f magnitude the positive y-direction. Determine the magnitude and `B =0.020 T` is in direction of the magnetic force on each segment.
View SolutionFind the ratio of magnetic dipole moment and magnetic field at the centre of a disc. Radius of disc is `R` and it is rotating at constant angular speed o about its axis. The disc is insulating and uniformly charged
View SolutionA megnetic dipole with a dipole moment of magnitude `0.020 J/T` is released from rest in a tutiliform magnetic field of magnitude `52 mT`. The rotation of the dipole due to the magnetic force on it is unimpeded. When the dipole rotates through the orientations where its dipole moment is aligned with the magnetic field, its kinetic energy is `0.80 mJ`.
(a) What is the initial angle between the dipole moment and the magnetic field?
(b) What is the angle when the dipole is next (momentarily) at rest?
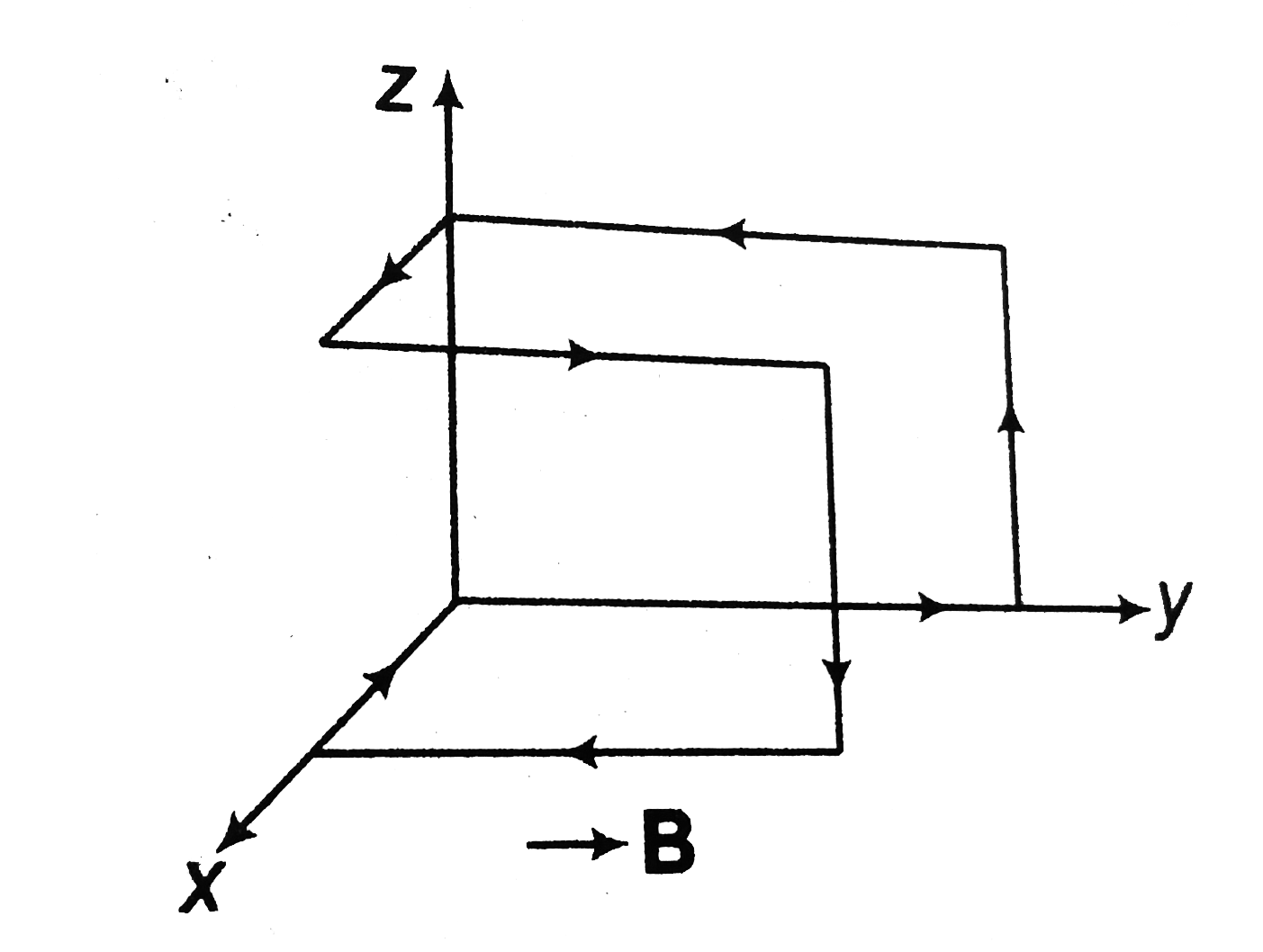
View SolutionA conductor carries a constant current `I` along the closed path `abcdefgha` involving `S` of the 12 edges each of length 1. Find the magnetic dipole moment of the closed path.
View SolutionGiven figure shows a coil bent with all edges of length `1 m` and carrying a current of `1 A`. There exists in space a uniform magnetic field of `2 T` in positive y-direction. Find the torque on the loop.
View SolutionA very long wire carrying a current `I = 5.0 A` is bent at right angles. Find the magnetic induction at a point lying on a perpendicular normal to the plane of the wire drawn through the Point of bending at a distance `l = 35 cm` from it.
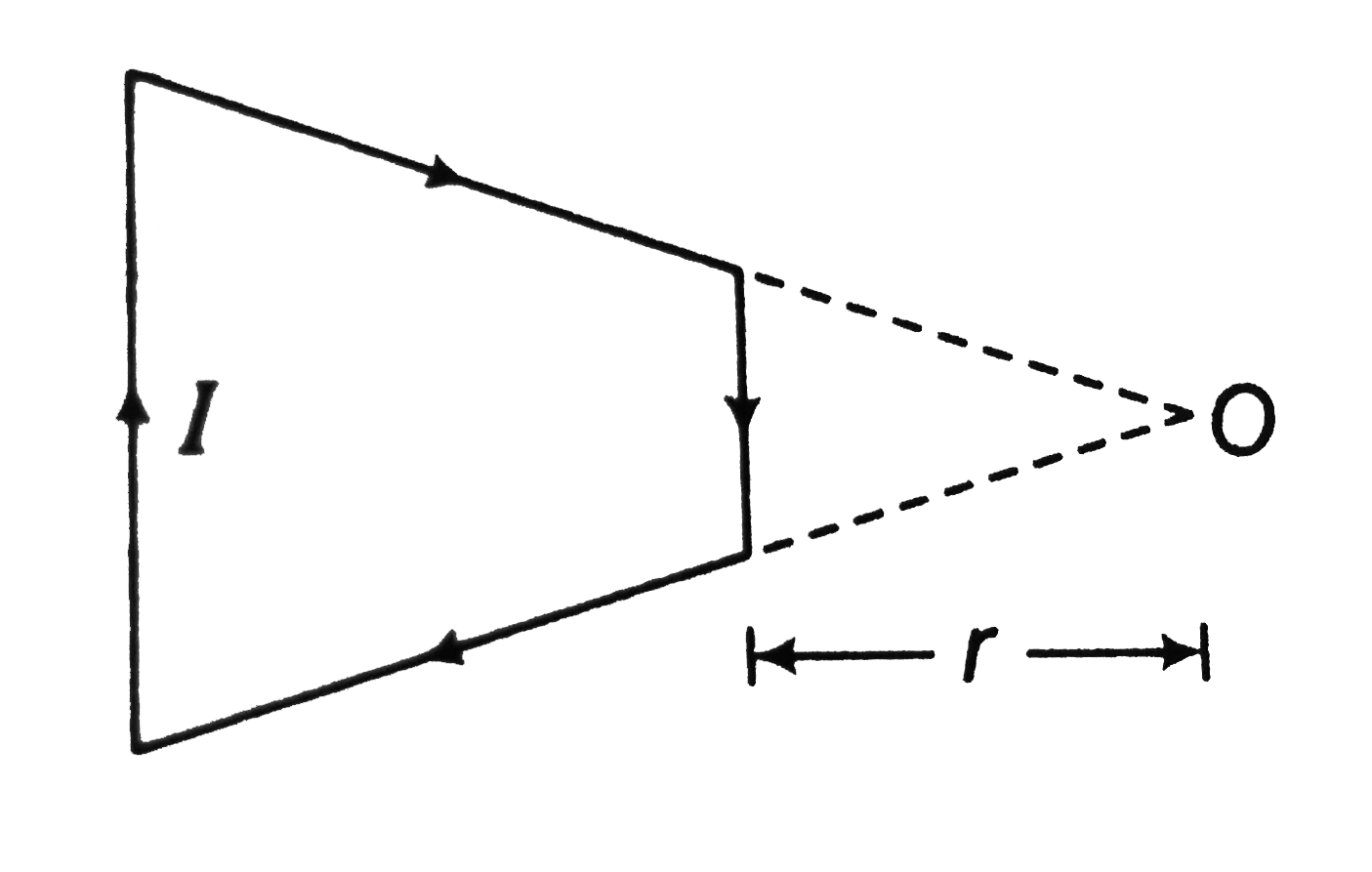
View SolutionA current `I = sqrt2` A flows in a circuit having the shape of isosceles trapezium. The ratio of the bases of the trapezium is 2. Find the magnetic induction B at symmetric point O in the plane of the trapezium. The length of the smaller base of the trapezium is `100 mm` and the distance `r=50mm`.
View SolutionTwo long mutually perpendicular conductors carrying currents `I_1` and `I_2` lie in one plane, Find the locus of points at which the magnetic induction is zero.
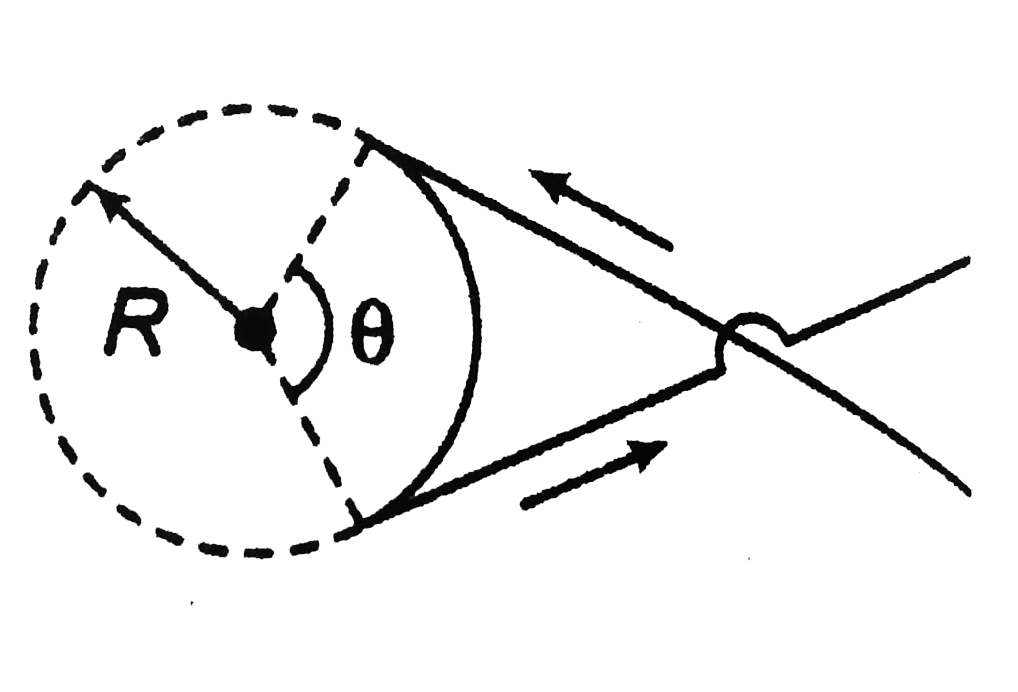
View SolutionA wire carrying current `i` has the configuration as shown in figure. Two semi-infinite straight sections, both tangent to the same circle, are connected by a circular arc of central angle theta, along the circumference of the circle, with all sections lying in the same plane. What must be for `B` to be zero at the centre of the circle?
View SolutionTwo long parallel transmission lines `40.0 cm` apart carry `25.0 A` and `75.0 A `currents. Find an locations where the net magnetic field of the two wires is zero if these currents are in
(a) the same direction (b) the opposite direction
View SolutionA closely wound coil has a radius of 6.00 cm and carries a current of `2.50 A`. How many turns must it have if, at a point on the coil axis `6.00 cm` from the centre of the coil, the magnetic field is `6.39 xx 10^-4T` ?
View Solution
Exercise questions and complete solutions for chapter MAGNETICS of DC PANDEY ENGLISH of Class 12