Complete Solutions to Exercises of chapter MAGNETIC FIELD of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MAGNETIC FIELD |
| HC VERMA | Exercises |
| Number Of Questions | 60 |
| Academic Year | 2023-24 |
An alpha particle is projected vertically upward a speed of `3.0 X 10^4 km s^(-1)` in a region where a magnetic field of magnitude 1.0 T exists in the direction south to north. Find the magnetic force that acts on the a particle.
View SolutionAn electron is projectd horizontally with a kinetic energy of 10 keV. A magnetic feld of strength `1.0X10^(-7)` T exists in the vertically upward direction. (a)will the electron deflect towards right or towards left of its motion? (b) calculate the sideways deflection of the electrion in travelling through 1m. make appropriate approximations.
View SolutionA magnetic field of `(4.0 X10^(-3)vec k)` T exerts a force of `(4.0veci +3.0vecj x 10^(-10)` N on a particle having a charge of `1.0X10^(-9)` C and going in the x-y plane. Find the velocity of the particle.
View SolutionAn experimenter's diary reads as follows: ''a charged particle is projected in a magnetic feld of `(7.0 veci - 3.0 vecj )X 10^(-3)` T. The acceleraation of the particle is found to be `(square veci +7.0 vec j) X10 ^(-6) ms^(-2)'. The number to left of `veci` in the last expression was not readable. What can this number be?
View SolutionA 10 g bullet having a charge of `4.00 muC` is fired at a speed of `270 ms^(-1)` in a horizontal direction. A vertical magnetic field of `500 muT` exists in the space. Find the deflection of the bullet due to the magnetic field as it travels through 100m. make appropriate approximations.
View Solutionwhen a proton is released from rest in a room, it starts with an initial acceleration `a_0` towards west . When it is projected towards north with a speed `v_0,` it moves with an initial acceleration `3a_0` towards west. Find the elecrtic field and the minimum possible magnetic field in the room.
View SolutionConsider a 10cm long protion of a straight wire carrying a current of 10 A placed in a magnetic field of 0.1 T making an angle of `53^@` with the wire. What magnetic force does the wire experience?
View SolutionA current of 2 A enters at the corner d of a square frame abcd of side 20 cm and leaves at the opposite corner b. A magnetic field B= 0.1 T exists in the space in a direction perpenducular to the plane of the frame as shown in Find the magnitude and direction of the magnetic forces on the four sides of the frame.

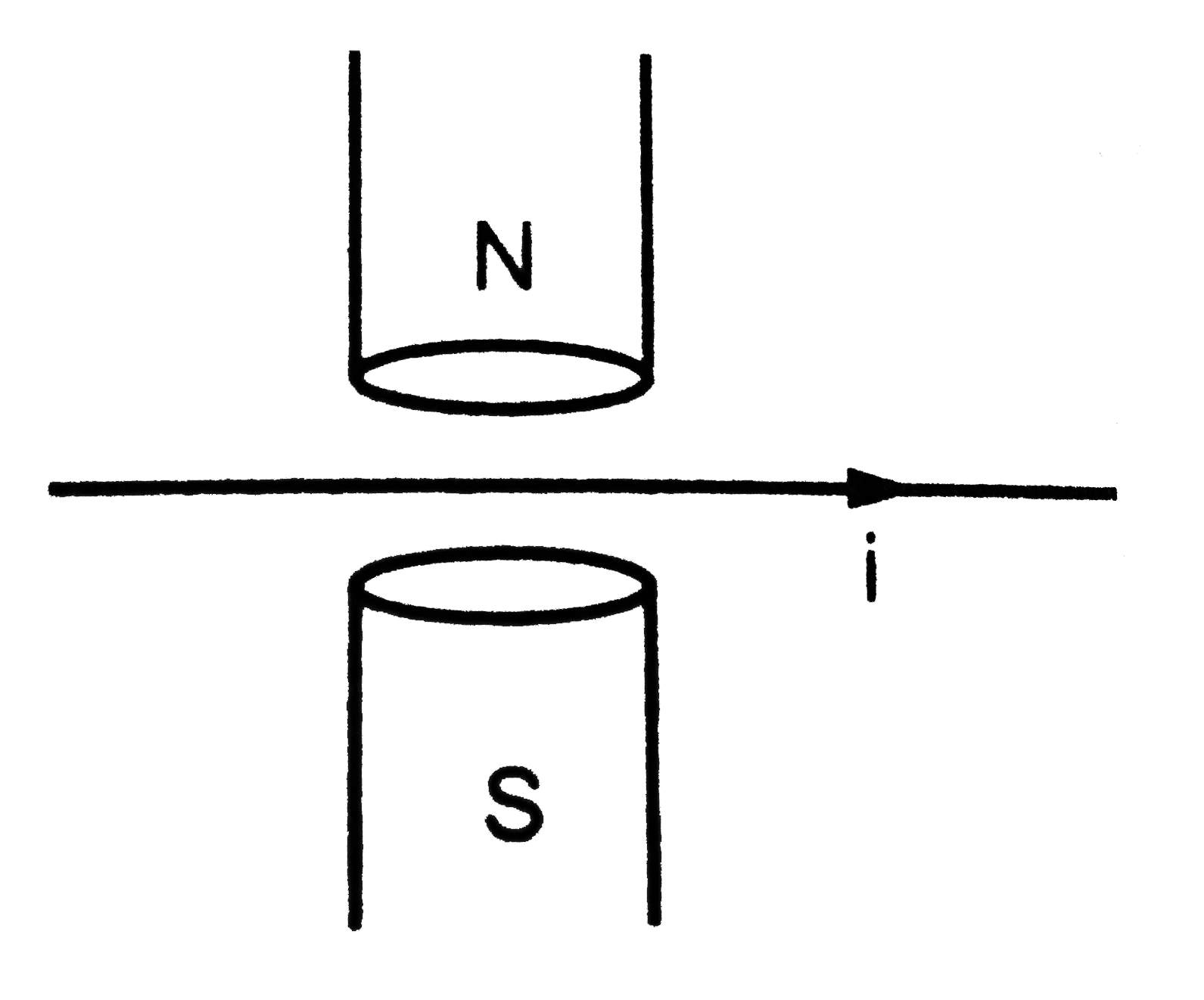
View SolutionA magnetic field of strength 1.0 T is produced by a strong electromagnet in a cylindrical region of radius 4.0 cm as shown in . A wire, carrying a current of 2.0 A, is placed perpendiuclar to and intersecting the axis of the cylindreical region. Find the magnitude of the force acting on the wire.
View SolutionA wire of length l carries a current I along the x-asis. A magnetic field exists which is given as `vecB=B_0(veci+vecj+veck)` T. find the magnitude of the magnetic force acting on the wire.
View SolutionA current of 5.0 A exists in the circuit shown in The wire PQ has a length of 50 cm the magnetic field in which it is immersed has a magnitude of 0.20 T. Find the magnetic force acting on the wire PQ.

View SolutionA circular loop of radius a, carrying a current I, is placed in a tow dimensional magnetic field. The centre of the loop coincides with the centre of the filed The strenght of the magnetic field at the pariphery of the loop is B. find the magnetic force on the wire.

View SolutionA hypthetical magnetic field existing in a region is given by `vecB= B_0 vece_r,` where `vec_r` denotes the uit vector along the redial direction. A circular loop of radus a, carrying a current I, is placed with its plane parallel to the x-y plane and the centre at (0,0, d) .Find the magnitude of the magnetic force acting on the loop.
View SolutionA rectangular wire-loop of width a is suspended from the insulated pan of a spring blance as shown in A current I exists in the anticlockwise direction in the loop. A magnetic field B exists in the lower region.Find the change in the tension of the spring if the current in the loop is reversed.

View SolutionA current loop of arbitrary shape lies in a uniform magnetic field B. show that the net magnetic force acting on the loop is zero.
View SolutionProve that the force acting on a current carrying wire, joining two fixed points a and b in a uniform magnetic field, is independent of the shape of the wire.
View SolutionA semicircular wire of radius 5.0 cm carries a current of 5.0 A. A magnetic field B of magnitude 0.50 T exists along the perpendicular to the plane of the wire. Find the magnitude of the magnetic force acting on the wire.
View SolutionA wire, carrying a current `i`, is kept in the `x-y` plane along the curve `y = A sin ((2pi)/(lambda) x)`. A magnetic field `B` exists in the z-direction. Find the magnitude of the magnetic force on the portion of the wire between `x = 0 and x = lambda`.
View SolutionA rigid wire consists of a semicircular portion of radius R and two straight sections the wire is partially immersed in a perpendicualr magnetic field B as shown in the figure. Find the magnetic force on the wire if it carries a current `i`.
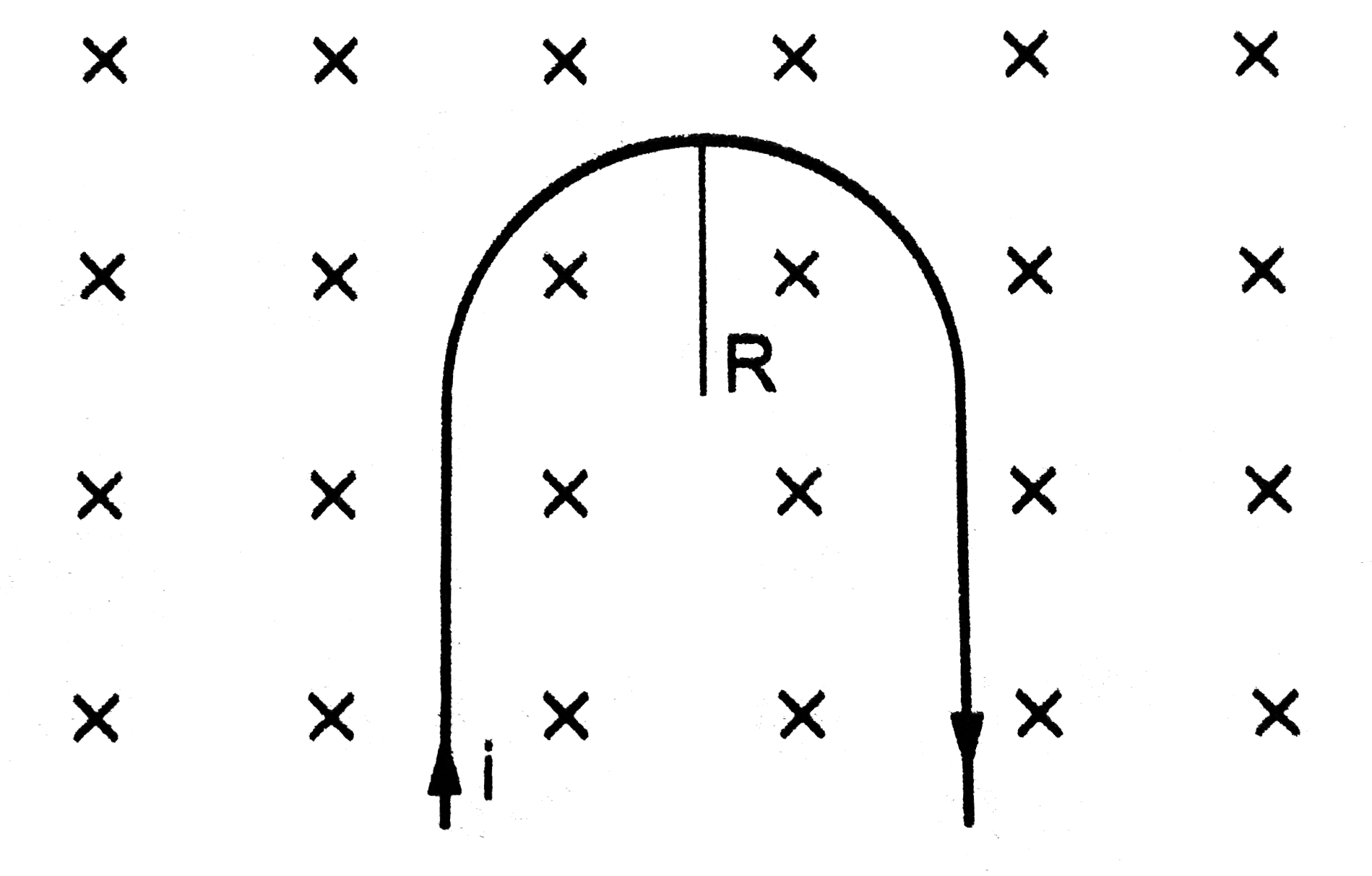
View SolutionA straight horizontal wire of mass 10mg and length 1.0 cm carries a current of 2.0 A. what minimum megnetic field B should be applied in the region so that the magnetic force on the wire may balance its weight?
View SolutionTwo metal strips, each of length, each of length l, are clamped parallel to each other on a horizontal floor with a separation b between them. A wire of mass m line on them perpendicularly as shown in figure. A vertically upward magnetic field of strenght B exists in the space. The matal strips are smooth but the cofficient of freiction between the wire and the floor is `mu`. A current i is established when the switch S is closed at the instant `t=0`. Discuss the motion of the wire after the switch is closed. How far away from the strips will the wire reach?

View SolutionA matel wire PQ of mass 10g lies at rest on two horizontal metal rails separated by 4.90 cm . A vertically downward magnetic field of magnitude 0.800 T exists in the space. The resistance of the circuit is slowly decreased and it is found that when the resistance goes below`20.0 Omega`, the wire PQ starts sliding on the rails. Find the coefficient of friction.

View SolutionA straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is `mu`. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
View SolutionA circular loop of radius a, carrying a current I, is placed in a tow dimensional magnetic field. The centre of the loop coincides with the centre of the filed The strenght of the magnetic field at the pariphery of the loop is B. find the magnetic force on the wire.

View SolutionA ring of radius 0.1m is made out of thin metallic wire of area of cross section `10^(-6)m^(2)`. The ring has a uniform charge of `pi` coulombs. Find the change in the radius of the rig when a charge of `10^(-8)C` is placed at the center of the ring. Young's modulus of the metal is `2xx10^(11)Nm^(-2)`.
View SolutionThe magnetic field existing in a region is given by `vecB =B_0(1+(x)/(l))vec k.` A square loop of edge l and carrying a current I, is placed with its edges parallel to the x-y axes. Find the magnitude of the net magnetic force experienced by the loop.
View SolutionA conducting wire of length l, lying normal to a magnetic field B, moves with a velocity v as shown in (a) Find the average magnetic fore on a free electron of the wire. Due to this magnetic force, electrons concentrate at one end resulting in an electric field inside the wire. The redistribution stops when the electric force on the free electrons balances themagnetic force. Find the electric field developed inside the wire when the redistribution field developed inside the wire when the redistribution stops. (c) what potential difference is developed between the ends of the wire?
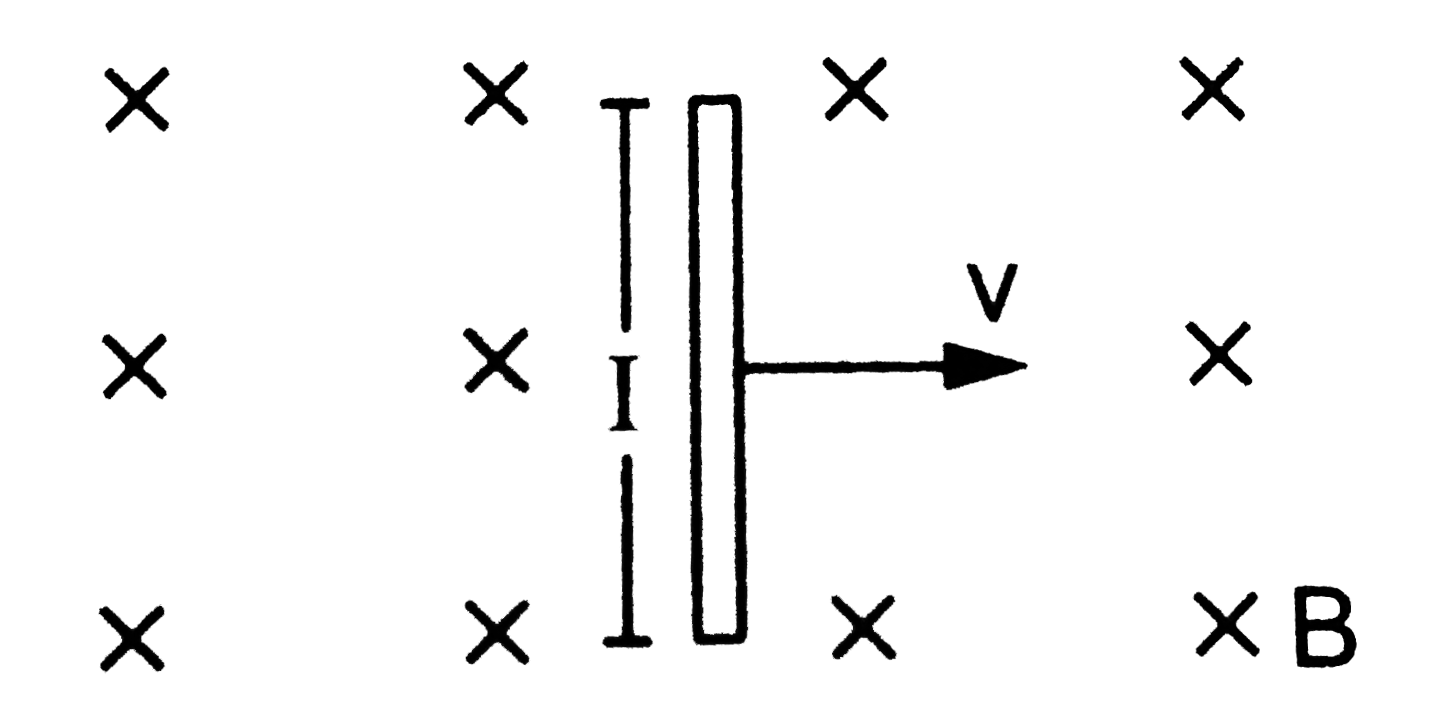
View SolutionA currrent I is passed through a silver strip of width d and area of cross section A. The number of free electrons per unit volume is n. (a) Find the drift velocity v of the electrons. (b) If a magnetic field B exists in the region as shown in what is the average magnetic force on the free electrons? (c) Due to the magnetic force, the free electrons get accumulated on one side of the conductor along its length. This produces a transverse electric field in the conductor which opposes the magnetic force on the electrons. Find the magnitude of the electric field which will be the potential diference developed across the width of the conductor due to the electron- accumulation? The appearance of a transverse emf, when a current-carrying wire is placed in a magnetic field, is called hall effect.

View SolutionA particle having a charge of `2.0X10^(-8) C` and a mass of `2.0X10^(-10)g` is projected with a speed of `2.0X10^3 ms^(-1)` in a region having a uniform magnetic field of 0.10 T. The velocity is perpendicular to the field. Find the radius of the circle formed by the particle and also the time period.
View SolutionA proton describes a circle of radius 1 cm in a magnetic field of strength 0.10 T. What would be the radius of the circle described by an a-particle moivng with the same speed in the same magnetic field?
View SolutionAn electron having a kinetic energy of 100eV circulates in a path of radius 10cm in a magnetic field. Find the magnetic field and the number of revolutons per second made by the electron.
View SolutionProtons having kinetic energy K emerge from an accelerator as a narrow beam. The beam is bent by a perpendicular magnetic field so that it just misses a plane target kept at a distance I in front of the accelerator. Find the magnetic field.
View SolutionA charged particle is accelerated thrught a potential difference of 12 kV and acquires a speed of `1.0X10^6 ms^(-1).` It is then injected perpendiuclarly into a magnetic field of strenght 0.2 T. find the radius of the circle described by it.
View SolutionDoubly ionized helium ions are projected with a speed of `10kms^(-1)` in a direction perpendicular to a uniformmagnetic field of magnitude 1.0 T. Find (a) the force acting on an ion, (b) the radius of the circle in which it ciruclates and ( c) the time taken by an ion to complete the circle.
View SolutionA proton is projected with a velocity of `3X10^6 m s ^(-1)` perpendicular to a uniform magnetic field of 0.6 T. find the acceleration of the proton.
View Solution(a) An electron moves along a circle of radius 1m in a perpendicular magnetic field of strength 0.50 T. What would be its speed? Is it reasonable?(b) If a proton moves along a circle of the same radius in the same magnetic field, what would be its speed?
View SolutionA particle of mass m and positive charge q, moving with a uniform velocity v, enters a magnetic field B as shown in (a) Find The radius of the circular arc it describes in the magnetic field. (b) find the angle subtended by the arc at the center. (c ) How long does the particle stay inside the magnetic field? (d) Solve the three parts of the above problem if the charge q on the particle is negative.
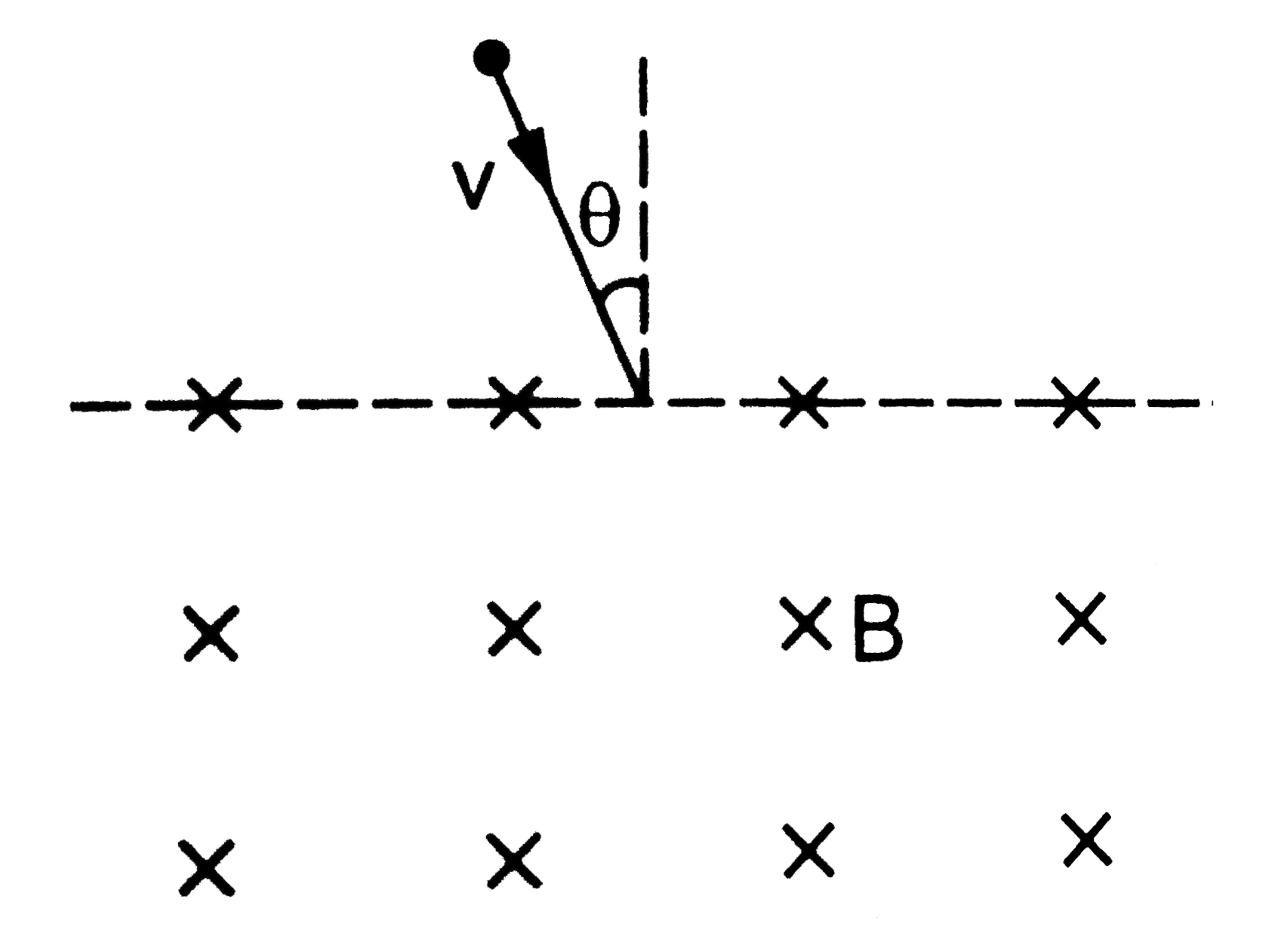
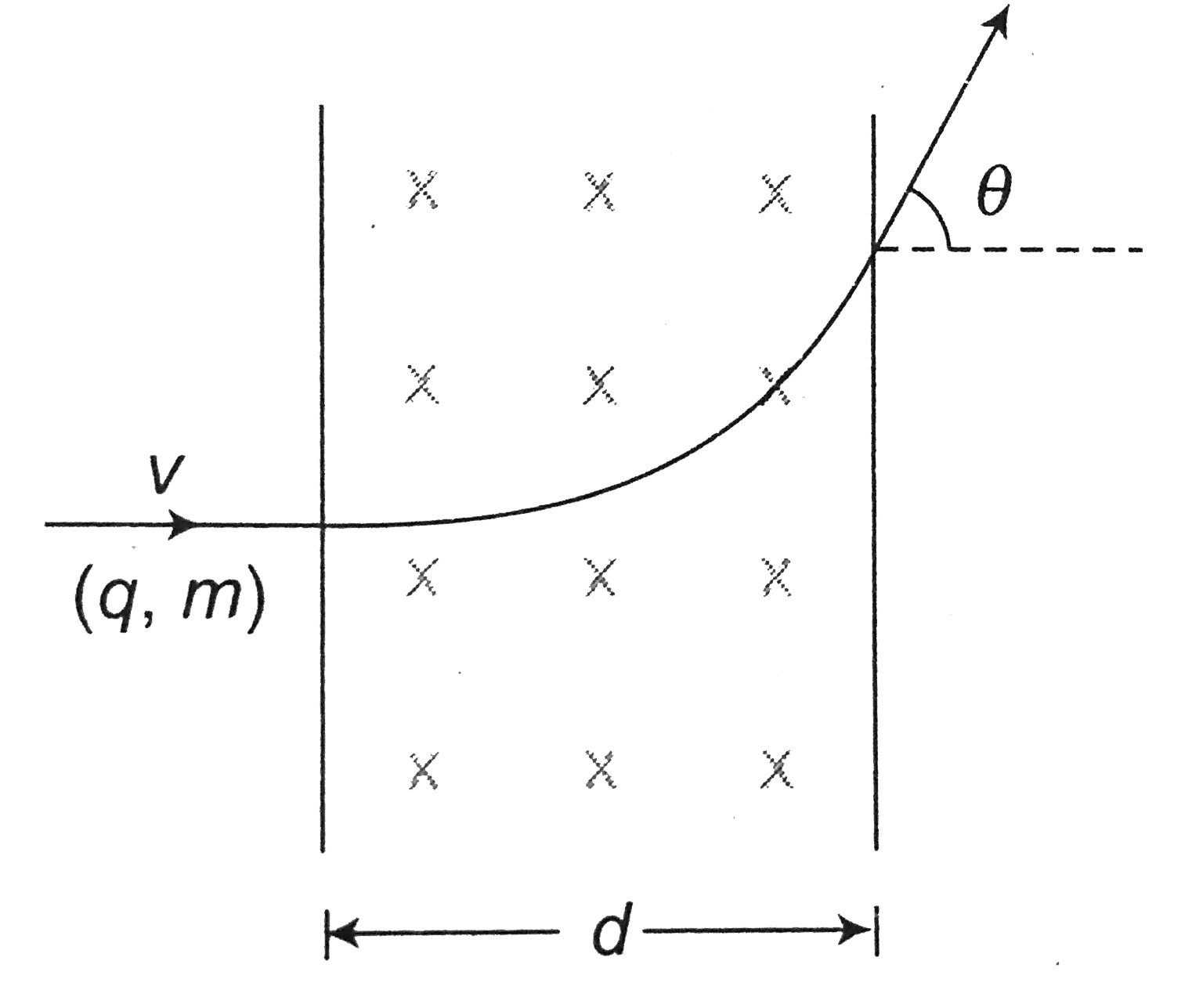
View SolutionA charged particle `(q, m)` enters perpendicular in a uniform magnetic field `B` and comes out field as shown. Find the angle of deviation `theta` for particle to cross magnetic field will be
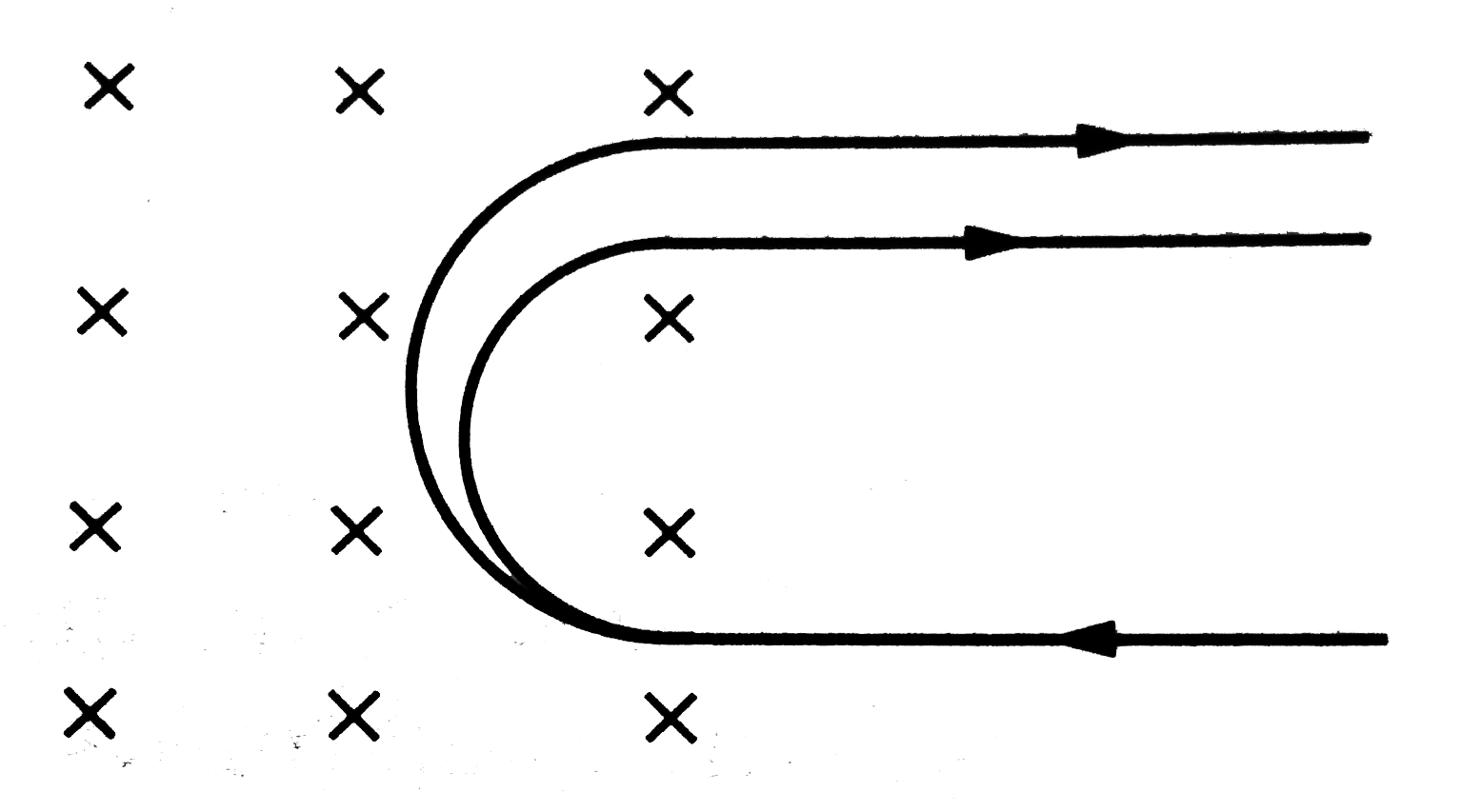
View SolutionA narrow beam of singley charged carbon ions, moving at a constant velocity of `6.0 X10^4 ms^(-1),` is sent perpendicularly in a rectangular region having uniform magnetic field B=0.5 T . It is found that two beams emerge from the field in the backward derection, the separations from the incident beam being 3.0 cm and 3.5cm. Identify the isotopes persent in the ion beam. Take the mass of an ion = `A(1.6 X10^(-27)` kg, where A is the mass number.
View SolutionFe^+ ions are accelerated through a potential difference of 500 V and are injected normally into a homogeneous magnetic field B of strength 20.0 m T. Find the radius of the circular paths followed by the isotopes with mass numbers 57 and 58. Take the mass of an `ion = A (1.6 X10^(-27)` kg where A is the mass number.
View SolutionA narrow beam of singly charged potassium ions of kinetic energy 32keV is injected into a region of width 1.00 cm having a magnetic field of strength 0.500 T as shown in . The ions are collected at a screen 95.5cm away from the field region. If the beam contains isotopes of atomic weights 39 and 41, find the separation between the points where these isotopes strike the screen. Take the mass of a potassium `ion= A (1.6 X 10^(-27)`) kg where A is the mass number.

View SolutionShows a convex lens of focal length 12 cm lying in a uniform magnetic field B of magnitude 1.2 T parallel to its principal axis. A particle having a charge `2.0X 10^(-3) C` and mass `2.0 X 10^(-5)` kg is projected perpendiucular to the plane of the diagram with a speed of `4.8 ms ^(-1).` The particle moves along a circle with its centre on the principal axis at a distance of 18 cm from the lens. Show that the image of the particle goes along a circle end find the radius of thet circle.

View SolutionElectrons emitted with negligible speed from an electron gun are accelerated through a potential difference V along the x-axis. These electrons emerge from a narrow hole into a uniform magnetic field B directed along this axis. However. Some of the electrons emerging from the hole make slightly divergent angles as shown in fig., show that these paraxial electrons are refocused on the x-axis at a distance `sqrt(8pi^2 mV)/(eB^2)`.

View SolutionTwo particles, each having a mass m are placed at a separation d in a uniform magnetic field B as shown in they have opposite charges of equal magnitude q. at time t =0, the particles are projectd towards each other,each with a speed v. suppose the coulomb force between the charges is switched off. (a) Find the maximum value `v_m` of the projection speed so that the two particles do not collide. (b) What would be the minimum and maximum separation between the particles if `v = v_m /2?` (c) At what instant will a collision occur between the particles if `v = 2v_m` ? (d) Suppose `v =2v_m` and the collision between the particles is completely inelastic. Describe the motion after the collision.

View SolutionA uniform magnetic field of magnitude 0.20 T exists in space from east to west what speed should a particle of mass 0.010 g and having a charge `1.0 X 10^(-5)C` be projected from south to north so that it moves with a uniform velocity?
View SolutionA particle moves in a circle of diamater 1.0 cm under the action of magnetic field of 0.40 T, An electric field of `200 V m^(-1)` makes the path straight. Find the charges/mass ratio of the particle.
View SolutionA proton goes undflected in a crossed and magnetic field (the fields are perpendicular to each other) at a speed of `2.0X10^5 ms^(-1).` The velocity is perpendicular to both the fields. When the electric field is switched off, the proton moves along a circle of radius 4.0 cm. Find the magnitudes of the electric and the magnetic fields. take the mass of the proton `=1.6 X10^(-27)` kg.
View SolutionA particle having a charge of `5.0 mu C` and a mass of `5.0 X 10^(-12)kg` is projected with a speed of `1.0km s^(-1)` in a magnetic field of a magnetic field of magnitude 5.0 m T. The angle between the magnetic field and the velocity is `sin^(-1)(0.90)`. show that the path of the particle will be a helix. Find the diameter of the helix and its pitch.
View SolutionA proton projected in a magnetic field of 0.020 T travels along a helical path of radius 5.0 cm and pitch 20 cm. Find the components of the velocity of the proton along and perpendicular to the magnetic field. Take the mass of the proton` =1.6X10^(-27)`kg.
View SolutionA particle having mass m and charge q is released from the origin in a region in which electric field and magnetic field are given by
` vecB =- B_0vecJ and vecE - E_0 vecK.`
Find the speed of the particle as a function of its z-coordinate.
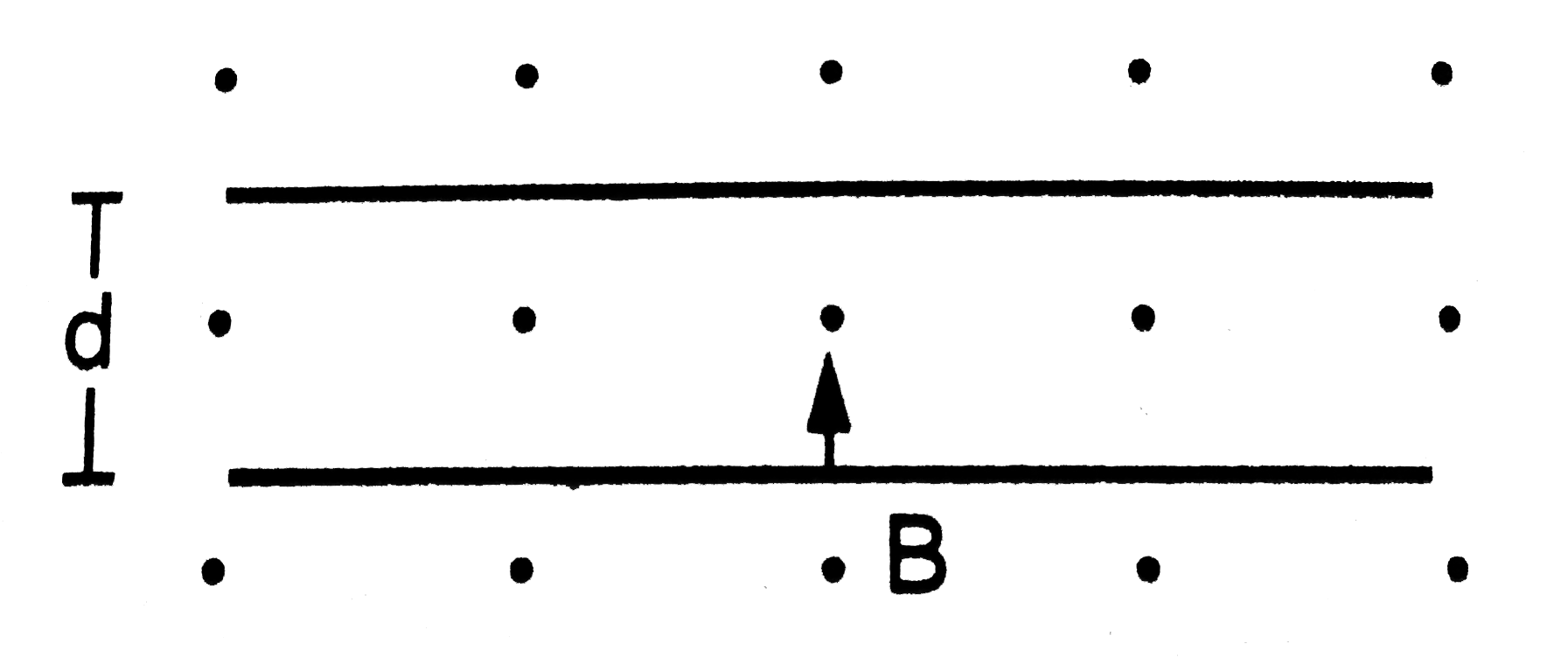
View SolutionAn electron is emitted with negligible speed from th nagative plate of a parallel plate capacitor charged ot a potential difference V. The separtion between the plates is d and a magnetic field B exists in the space as shown in . Show that the electron will fail to strike the upper plate if ltdgt `((2m_e V)/(eB_0^2))^(1/2)`.
View SolutionA rectangular coil of 100 turns has length 5 cm and width 4 cm. it is placed with its plane parallel to a uniform magnetic field and a current of 2 A is sent through the coil. Find the magnitude of the magnetic field B, if the torque acting on the coil is `0.2 Nm^(-1).`
View SolutionA 50 turn circular coil of radius 2.0 cm carrying a current of 5.0 A is rotated in a magnetic field of strength 0.20 T. (a) What is the maximum torque that acts on the coil? (b) in a particular position of the coil, the torque acting on it is half of this maximum. What is the angle between the magnetic field and the plane of the coil?
View SolutionA rectangular loop of sides 20 cm and 10 cm carries a current of 5.0 A. A uniform magnetic field of magnituded 0.20 T exists parallel ot the longer side of the loop (a) What is the force acting on the loop? (b) what is the torque acting on the loop?
View SolutionA circular coil of radius 2.0 cm has 500 turns in it and carries a current of 1.0 A . Its axis makes an angel of `30^@` with the uniform magnetic field of 0f magnitude 0.40 T that exists in the space. Find the torque acting on the total.
View SolutionA circular loop carrting a current a current I has wire of total length L. A uniform umagnetic field B exists parallel to the plane of the loop. (a ) find the trouque on the loop.(b) If the sme length of the wire is used to form a squar loop, what would be the torque? Which is larger?
View SolutionA square coil of edge I having n turns carries a curent i. it is kept on a smooth horizontal plate. A uniform magnetic field B exists in a direction parallel to an edge the total mass of the coil is M. What should be the minimum value of B for which the coil will start tipping over?
View Solutionconsider a nonconducting ring of radius r and mass m which has a total charge q distributed uniformly on it the ring is rotated about its axis with an angular speed `omega`. (a) Find the equivalent electric current in the ring (b) find the magnetic moment `mu` of the . (c) show that`mu=(q)/(2m)` where l is the angular momentum of the ring about its axis of rotation.
View SolutionConsider a non conducting plate of radius `a` and mass `m` which has a charge `q` distributed uniformly over it, The plate is rotated about its own axis with a angular speed `omega`. Show that the magnetic moment `M` and the angular momentum `L` of the plate are related as `(M)/(L)=(q)/(2m)`.
View SolutionConsider a non conducting plate of radius `a` and mass `m` which has a charge `q` distributed uniformly over it, The plate is rotated about its own axis with a angular speed `omega`. Show that the magnetic moment `M` and the angular momentum `L` of the plate are related as `(M)/(L)=(q)/(2m)`.
View Solution
Exercises questions and complete solutions for chapter MAGNETIC FIELD of HC VERMA PHYSICS (ENGLISH) of Class 12