Complete Solutions to Photometry And Geometrical Optics of chapter OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | OPTICS |
| IE IRODOV | Photometry And Geometrical Optics |
| Number Of Questions | 62 |
| Academic Year | 2023-24 |
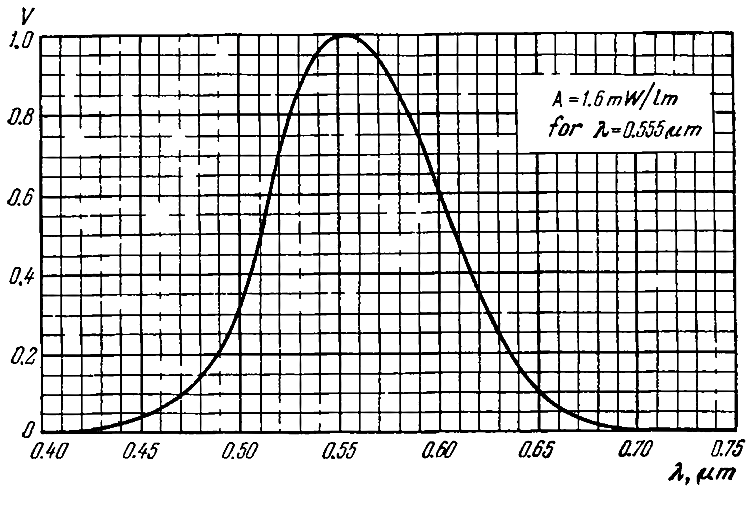
Making use of the spectral response curve for an eye (see Fig.), find :
(a) the energy flux corresponding to the luminous flux of `1.0 1m` at the wavelength `0.51` and `0.64mu m`,
(b) the luminous flux corresponding to the wavelength interval from `0.58` to `0.63 mu m` if the respective energy flux, equal to `Phi = 4.5 mW`, is unifromly distributed over all wavelengths of the interval. The function `V (lambda)` is assumed to be linear in the given spectral interval.
 13:15View Solution
13:15View SolutionA point isotropic source emits a luminous flux `Phi = 10 1m` with wavelength `lambda = 0.59 mu m`. Find the peak strength values of electric and magentic fields in the luminous flux at a distance `r = 1.0 m` from the osurce. Make use of the curve illustrated in Fig.
 06:12View Solution
06:12View SolutionFind the mean illuminance of the irradiated part of an opaque sphere receiving
(a) a parallel luminous flux resulting in illuminance `E_(0)` at the point of normal incidence,
(b) light from a point isotropic source located at a distance `l = 100 cm` from the cnetre of the sphere, the radius of the sphere is `R = 60 cm` and the luminous intensity is `I = 36 cd`.09:55View SolutionDetermine the luminosity of a surface whose luminance depends on direction as `L = L_(0) cos theta`, where `theta` is the angle between the radiation direction and the normal to the surface.
05:05View SolutionA certain luminous surface obeys Lambert's law. Its luminance is equal to `L`. Find:
(a) the luminous flux emitted by a element `DeltaS` of this surface into a cone whose axis is normal to the given element and whose aperture angle is equal to `theta`,
(b) the luminosity of such a source.04:04View SolutionAn illuminant shaped as a plane horizontal disc `S = 100 cm^(2)` in area is suspended over the centre of a round table of radius `R = 1.0 m`. Its luminance does not depend on direction and is equal illuminant be suspended to provide maximum illuminance at the circumference of the table ? How great will that illuminance be? The liuminant is assumed to be a point source.
07:45View SolutionA point source is suspended at a hight `h = 1.0 m` over the centre of a round table of radius `R = 1.0 m`. The luminous intensity `I` of the source depends on direction so that illuminance at all points of the table is the same. Find the function `I (theta)`, where `theta` is the angle between the radiation direction and the vertical, as well as the luminous flux reaching the table if `I (0) = I_(0) = 100 cd`.
06:03View SolutionA vertical shaft of light from a projector forms a light spot `S = 100 cm^(2)` in area on the celling of a round room of radius `R = 2.0 m`. The illuminance of the spot is equal to `E = 1000 1x`. The reflection coeffiecient of the celling is equal to `rho = 0.80`. find the maximum illuminance of the well produced by the light reflected from the celling. the reflection is assumed to obey Lambert's law.
07:44View SolutionA luminous done shaped as a hemisphere rests on a horizontal plane. Its luminosity is uniform. Determine the illuminance at the centre of that plane if its luminance equals `L ` and is independent of direction.
06:04View SolutionA Lambert source has the from of an infinite plane. Its luminance is equal to `L`. Find the illuminance of an area element oriented parallel to the given source.
05:32View SolutionAn illuminant shaped as a plane horizontal disc of raiud `R = 25 cm` is suspended over a table at a hight `h = 75 cm`. The illuminance of the table below the cnetre of the illuminant is equal to `E_(0) = 70 Ix`. Assuming the source to obey Lambert's law, find its luminosity.
08:51View SolutionA small lamp having the form of a unfromly luminous sphere of radius `R = 6/0 cm` is suspended at a height `h = 3.0 m` above the floor. The luminance o fthe lamp is equal to `L = 2.0. 10^(4) cd//m^(2)` and is independent of direction. Find the illuminance of the floor directly below the lamp.
14:18View SolutionWrite the law of reflection of a light beam from a mirror in vector from, using the directing unit vectors `e` and `e'` of the incident and reflected beams and the unit vector `n` of the outside normal to the mirror surrfcae.
04:21View SolutionDemostrate that a light beam reflected from three mutually perpendicular plane mirrors in succession reverses its direction.
05:23View SolutionAt what value of the angle of incident `theta_(1)` is a shaft of light reflected from the surface of water perpendicular to the refracted shaft?
02:27View SolutionTwo optical media have a plane boundary between them. Suppose `theta_(1 cr)` is the critical angle of incidence of a beam and `theta_(1)` is the angle of incidence at which the refracted beam is perpendicular to the reflected one (the beam is assumed to come from an optically denser medium). Find the relective index of these media if `sin theta_(1 cr)//sin theta_(1) = eta = 1.28`.
06:43View SolutionA light beam falls upon a plane-parallel glass plate `d = 6.0 cm` in thickness. The angle of incidence is `theta = 60^(@)`. Find the value of deflection of the beam which passed through that plate.
05:59View SolutionA man standing on the bottom. The depth o fthe swimming pool looks at a stone lying on the bootom. The depth of the swimming pool is equal to `h`. At what distance from the surafce of water is the image of the stone formed if the line of vision makes an angle `theta `with the normal to the surface?
12:26View SolutionDemonstrate that in a prism with small refracting angle `theta` the shaft of light deviates through the angle `alpha ~~(n - 1) theta` regard less of the angle of incidence, provided that the latter is also small.
08:54View SolutionDemonstrate that in a prism with small refracting angle `theta` the shaft of light deviates through the angle `alpha ~~(n - 1) theta` regard less of the angle of incidence, provided that the latter is also small.
09:05View SolutionThe least deflection angle of a ceratin glass prism is equal to its refracting angle. Find the latter.
01:41View SolutionFind the minimum and maximum deflectrion angls for a light ray passing through a glass prism with refracting angle `theta = 60^(@)`.
04:15View SolutionA trihedral prism with refracting angle `60^(@)` provides the least deflection angle `37^(@)` in air. Find the least deflection angle of that prism in water.
03:52View SolutionA light ray composed of two monochromatic components passes through a trihedral prism with refracting angle `theta = 60^(@)`. Find the angle `Delta alpha` between the components of the ray after its passage through the prism if their respective indies of refraction are equal to `1.515` and `1.520`. the prism is oriented to provide the least deflection angle.
07:30View SolutionUsing Fermat's principle derive the laws of deflection and refraction of light on the plane interface between two media.
07:30View SolutionBy means of plotting find :
(a) the path of a light ray after reflectin from a concave and convex spherical mirrors (see Fig. where `F` is the focal point, `OO'` is the optical axis) ,

(b) the positions of the mirror and its focal point in the cases illunstrated in Fig. where `P` and `P`' are the conjugate points.
 03:56View Solution
03:56View SolutionDetermine the focal length of a concave mirror if:
(a) with the distance between an object and its image being equal to `l = 15 cm`, the transverse magnification `beta =02.0`,
(b) in a certain position of the object the transverse magnification is `beta_(1) =-0.50` and in another position displaced with respect to the former by a distance `l = 5.0 cm` the transverse magnification `beta_(2) = - 0.25`.09:26View SolutionA point source with luminous intensity `I_(0) = 100 cd` is positioned at a distance `s = 20.0 cm` from the crest of a concave mirror with focal length `f = 25.0 cm`. Find the luminous intensity of the reflected ray if the reflection coefficient of the mirror is `rho = 0.80`.
07:32View SolutionProceeding from Fermat'sprinciple derive the refraction formula for paraxial rays on a spherical boundary surface of radius `R` between media with refractive indices `n` and `n'`.
12:18View SolutionA parallel beam of light falls from vacuum on a surface enclosing a medium with refractive3 index `n` (Fig.) Find the shape of that surface, `x(r )` if the beam is brought into focus at the point `F` at a distance `f` from the crest `O`. What is the maximum radius of a beam that can still be focussed ?
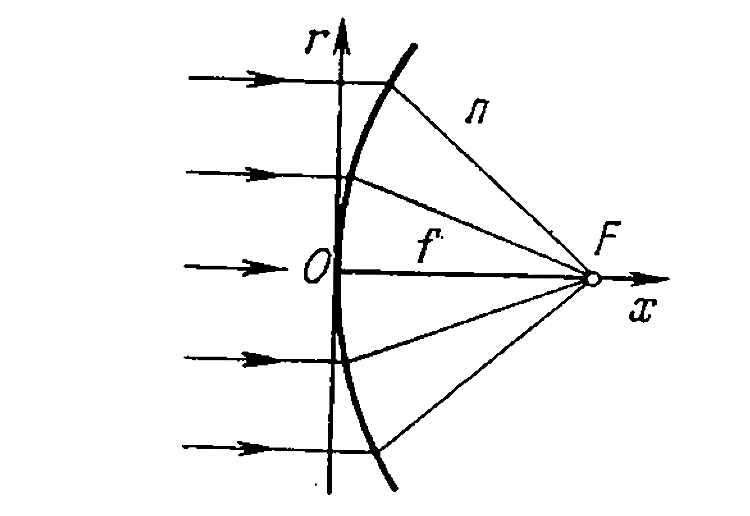 09:52View Solution
09:52View SolutionA point source is located at a distance of `20 cm` from the front surface of a symmetrical glass biconvex lens. The lens is `5.0 cm` thick and the curvature radius of its surfaces is `5.0 cm`. How far beyond the rear surface of this lens is the image of the source fromed ?
05:49View SolutionAn object is placed in front of convex surface of a glass plano-convex lens of thickness `d = 9.0 cm`. The image of that object is formed on the plane surface of the lens serving as a screen. Find:
(a) the transverse magnification if the curvature radius of the lens's convex surface is `R = 2.5 cm`,
(b) the image illuminance if the luminance of the object i s`L = 7700 cd//m^(2)` and the entrance apertune diameter of the lens is `D = 5.0 mm`, losses of light are negligible.09:49View SolutionFind the optical power and the focal lengths
(a) of a thin glass lens in liquid with refractive index `n_(0) = 1.7` if its optical power in air is `Phi_(0) = 5.0 D`,
(b) of a thin symmetrical biconvex glass lens, with air on one side and water on the other side, if the optical power of that lens in air is `Phi_(0) = + 10D`.13:05View SolutionBy means of plotting find :
(a) the path of a ray of light beyound thin converging and diverging lenses (Fig. where `OO'` is the optical axis, `F` and `F'` are the front and rear focal points),

(b) the position of a thin lens and its focal points if the position of the optical axis `OO'` and the positions of the cojugate3 points `P, P` (see Fig.) are knows , the media on both sides of the lenses are identical,
(c ) the path of ray `2` beyond the converging and diverging lenses (Fig. ) if the path of ray `1` and the positions of the lens and of its
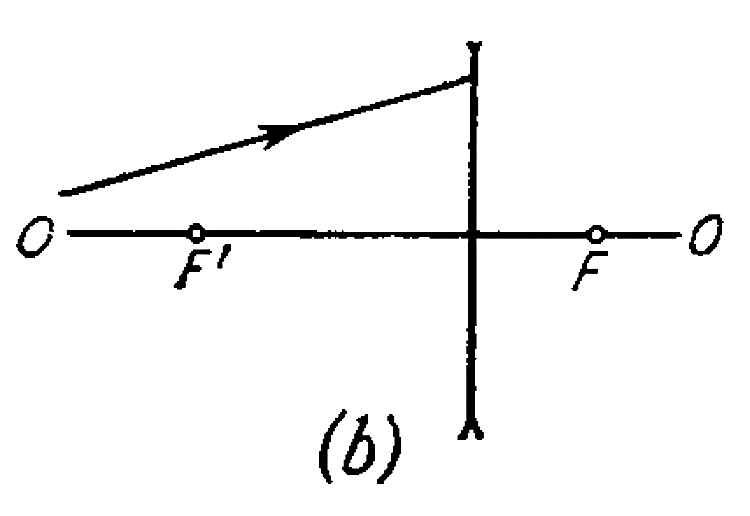
optical axis `OO'` are all known, the media on both sides of the lenses are identical.View SolutionA thin converging lens with focal length `f = 25 cm` projects the image of an object on a screen removed from the lens by a distance `l == 5.0 m`. Then the screen was draws closer to the lens by a distance `Delta l = 18 cm`. By what distance should the object be shifted for its image to become sharp again ?
07:06View SolutionA source of light is located at a disatnce `l = 90 cm` from a screen. A thin converging lens provides the sharp image of the source when placed between the source of light and the screen at two positions. Determine the focal length o fthe lens if
(a) the distance between the two positions of the lens is `Delta l = 30 cm`,
(b) the transverse diamensions of the image at one position o fthe lens are `eta = 4.0` greater than those at the pther position.09:36View SolutionA thin converging lens is placed between an object and a screen whose the sharp image of the object is formed on the screen. Find the transverse diamension of the object if at one position of the lens the image diamension equals `h' = 2.0 mm` and at the other, `h'' = 4.5 mm`.
03:41View SolutionA thin converging lens with aperture ratio `D : f = 1 : 35 (D` is the lens diameter, `f` is its focal length) provided the image of a sufficiently distance object on a photographic plate. The object luminance is `L = 260 cd//m^(2)`. The losses of light in the lens amount to `alpha = 0.10` . Find the illuminance of the image.
07:17View SolutionHow does the illuminance of a real image depend on diameter `D` of a thin converging lens if that image is observed
(a) directly,
(b) on a white screen backscatting according to Lamber's law ?10:47View SolutionThere are two thin symmetrical lenses : one is converging , with refractive index `n_(1) = 1.70`, and the other is diverging with refractive index `n_(2) = 1.51`. Both lenses have the same curavature close together and submerged into whater. What is the focal length of this system in water ?
07:06View SolutionDetermine the focal length of a concave spherical mirror which is manufactured in the form of a thin symmetric biconvex glass lens one of whose surfaces is silvered. The curvature radius of the lens surface is `R = 40 cm`.
05:31View SolutionFigure illustrates an aligned system consisting of three thin lenses. The system is located in air. Determine:
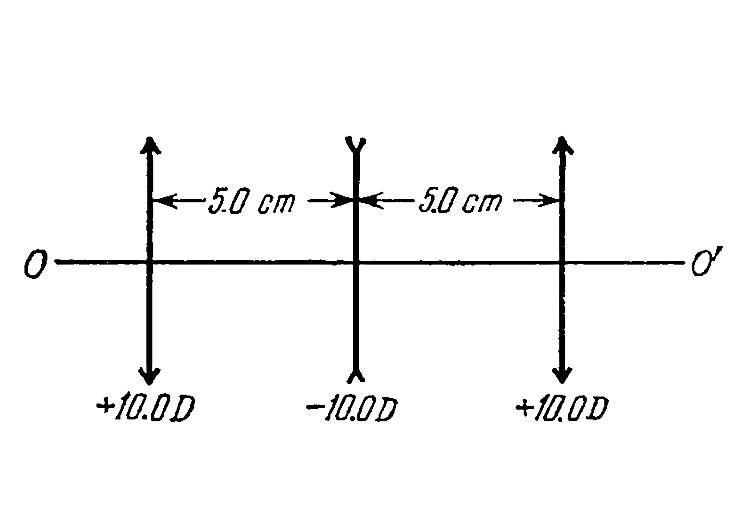
(a) the position of the point of convergence of a parallel incoming from the left after passing through the system,
(b) the distance between teh first lens and a point lying on the axis to the left of the system, at which that point and its image are located symmetrically with respect to the lens system.13:04View SolutionA Galilean telescope of `10`-fold magnification has the length of `45 cm` when adjusted to infinity. Determine :
(a) the focal lengths of the telescope's objective and ocular,
(b) by what distance the ocualr should be displaced to adjust the telescope to the distance of `50 m.`03:42View SolutionFind the magnification of a Keplerian telescope adjusted to infinity if the mounting of the objective has s diamter `D` and the image of that mounting formed by the telescope's ocular has a diameter `d`.
03:13View SolutionOn passing thorugh a telescope a flux of light increases its intensity `eta = 4.0.10^(4)` times. Find the angular dimension of a distance object if its image formed by that telescope has an angualr dimension `Psi = 2.0^(@)`.
03:22View SolutionA Keplerian telescope with magnification `T = 15` was submerged into water which filled up the inside of the telescope. To make the system work as a telescope again within the former dimensions, the objective was replaced. What has the magnification of the telescope become equal to ? the refractive index of the glass of which the ocular is made is equal to `n = 1.50`.
06:03View SolutionAt what magnification `T` of a telescope with a diameter of the objective `D = 6.0 cm` is the illuminance of the image of an object on the retina not less than without the telescope ? The pupil diameter is assumed do be equal to `d_(0) = 3.0 mm`. The losses of light in the telescope are negligible.
07:34View SolutionThe optical powers of the objective and the ocular of a microscope are equal to `100` and `20 D` respectively. The microscope magnification is equal to `50`. What will the magnification o fthe microscope be when the distance between the objected and the ocaular is increased by `2.0 cm`?
03:44View SolutionA microscople has numberical apertune `sin alpha = 0.12`, where `alpha` is the aperture angle subtended by the entrance pupil of the microscope. Assuming the diameter of an eye's pupil to be equal to `d_(0) = 4.0 mm` determine the microscope magnification at which
(a) the diameter of the beam of light coming from the microscope is equal to the diameter of the eye's pupil,
(b) the illuminance of the image on the retina is independent of magnification (consider the case when the beam of light passing through teh sysytem ''microscope-eye'' is bounded by the mounting of the objective).12:18View SolutionFind the positions of the perinciple planes, the focal and model points of a thin biconvex symmetric glass lens with curvature radius of its surfaces equal to `R = 7.50 cm`. There is air on one side of the lens and water on the other.
10:22View SolutionAn optical system is located in air. Let `OO`' be its optical axis, F' and F' are the front and rear focal points, H and H' are the front and rear principle planes, `P` and P' are the conjugate points. By means of plotting find:
(a) the position `F'` and `H`' (Fig.),
(b) the position of the point `S`' conjugate to the point `S` (Fig.),
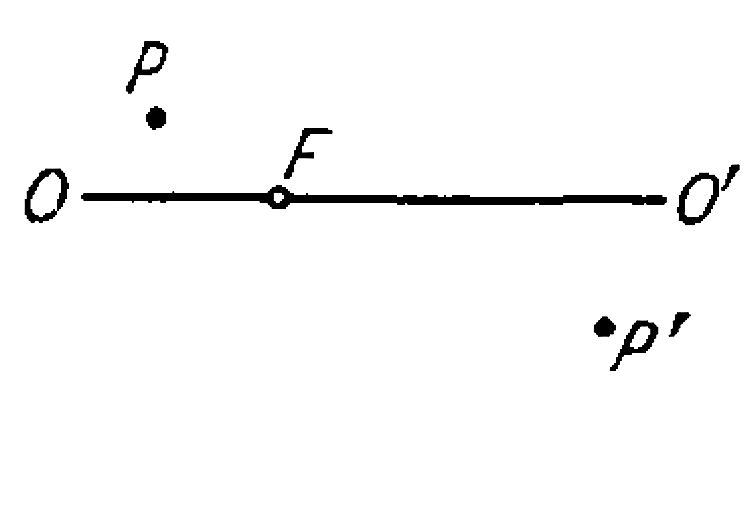
(c) the positions `F, F`', and `H`' (Fig. where the path of the ray of light is shown before and after pasing through the system).View SolutionSuppose `F`' and `F`' are the front and rear focqal points of an optical system, and `H`' and `H'` are its front and rear principle points. By means of plotting relative positions of the points `S, F, F', H,` and `H'`:
(a) `FSHH'F'`, (b) `HSF'FH'`, (c) `H'S'FH`, (d) `F'H'SHF`.19:01View SolutionA telephoton lens consists of two lenses, the front converging lens and the rear diverging lens with optical power `Phi_(1) = + 10D` and `Phi_(2) = -10D`. Find:
(a) the focal length and the positions of principle axes of that system if the lenses are seperated by a distance `d = 4.0 cm`, (b) the distance `d` between the lenses at which the ratio of a focal length `f` of the system to a distance `l` between the converging lens and the rear principle focal points is the highest. what is this ratio equal to ?11:34View SolutionCalculate the positions of the principle planes and focal points of a thick convex-concave glass lens if the curvature radius of the convex surface is equal to `R_(1) = 10.0 cm` and of the concave surface to `R_(2) = 5.0 cm` and the lens thickness is `d = 3.0 cm`.
05:29View SolutionAn aligned optical system consists of two thin lenses with focal lengths `f_(1)` and `f_(2)`, the distance between the lenses being equal to `d`. The given system has to be replaced by one thin lens which, at any position of an object, would provide the same transverse magnification as the system. what must the focal length of this lens be equal to and in what position must it be placed with respect to the two-lens system?
07:22View SolutionA system consists of a thin symmetrical converging glass lens with the curvature radius of its surfcaes `R = 38 cm` and a plane mirror oriented at right angles to the optical axis of the lens. What is the optical power of this system when the space between the lens and the mirror is filed up with water ?
06:46View SolutionAt what thickness will a thick convex-cancave glass lens in air
(a) serve as a telescope provided the curvature radius of its convex surface is `DeltaR = 1.5 cm` greater than that of its concave surface?
(b) have the optical equal to `-1.0 D` if the curvature radii of its convex and concave surfaces are equal to `10.0` and `7.5 cm` respectively ?10:09View SolutionFind the poistions of the principle planes, the focal length and the sign of the optical power of a thick convex-concave glass lens
(a) whose thickness is equal to `d` and curvature radii of the surfaces are the same and equal to `R`,
(b) whose refractive surfaces are concentric and have the curvarure radii `R_(1)` and `R_(2) (R_(2) gt R_(1))`.09:17View SolutionA telephoton system consists of two glass balls with radii `R_(1) = 5.0 cm` and `R_(2) = 1.0 cm`. What are the distance between the centres of the balls and the magnification of the system if the bigger ball serves as no objective ?
10:27View SolutionTwo identical thick symmetrical biconvex lenses are put close together. The thickness of each equals the curvature radius of its surfaces, i.e `d = R = 3.0 cm`. Find the optical power of this system in air.
07:43View SolutionA ray of light propagating in an isotropic medium with refractive index `n` varying gradually from point to points has a curvature radius `rho` determined by the formula
`(1)/(rho) = (del)/(del N) (In n)`,
where the derivative is taken with respect to the principle normal to the ray. Derivethis formula, assuming that is such a medium the law of refraction `n sin theta = ` const holds. Here `theta` is the angle between the ray and the direction of the vector `Delta n` at a given point.08:09View SolutionFind the curvature radius of a ray of light propagating in a horizontal direction close to the Earth's surface where the gradient of the refractive index in air is equal to approximately `3.10^(-8) m^(-1)`. At what value of that gradient would the ray of light propagate all the way round the Earth?
03:08View Solution
Photometry And Geometrical Optics questions and complete solutions for chapter OPTICS of IE IRODOV PHYSICS (HINGLISH) of Class 12
