Complete Solutions to Polarization Of Light of chapter OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | OPTICS |
| IE IRODOV | Polarization Of Light |
| Number Of Questions | 43 |
| Academic Year | 2023-24 |
A plane monochromatic wave of natural light with intensity `I_(0)` falls normally on a screen composed of two touching Polaroid half-planes. The principle direction of one Polaroid is parallel,and of the other perpendicular, to the boundary between them. What kind of diffraction pattern is formed behind the screen? What is the intensity of light behind the screen at the points of the plane perpendicualr to the screen and passing through the boundary between the Polaroids?
View SolutionA plane monochromatic wave of natural light with intensity `I_(0)` falls normally on an opaque screen with round hole corresponding to the first Fresnel zone for the observation point `P`. Find the intensity of light at the point `P` after the hole was converd with two identical Polaroids whose principle directions are mutually perpendicular and the boundary beween them passes
(a) along the diameter of the hole,
(b) along the circumference of the circle limiting the first half of the fresnel zone.View SolutionA beam of plane-polarized light falls on a polarizer which rotates about the axis of the ray with angular velocity `omega = 21rad//s`. Find the energy of light passing through the Polarizer per one revolution if the flux of energy of the incident ray is equal to `Phi_(0) = 4.0mW`.
04:33View SolutionA beam of natural light falls on a system or `N = 6` Nicolprisms whose transmission planes are turned each through an angle `varphi = 30^(@)` with respect to that of the foregoing prism. What fraction of luminous flux passes through this system ?
05:29View SolutionNatural light falls on a system of three identical in-line Polaroids the principle direction of the middle Polaroid forming an angle `varphi = 60^(@)` with those of two other Polaroids. The maximum transmission coefficient of each Polaroid is equal to `tau = 0.81` when plane-polarized light falls on them. How many times will the intensity of the light decrease after its passing through the system?
04:43View SolutionThe degree of polarization of partially polarized light is `P = 0.25`. Find the ratio of intensities of the polarized component of this light and the natural component.
03:14View SolutionA Nicol prism is placed in the way of partially polarized beam of light. When the prism is turned from the position of maximum transmission through an angle `varphi = 60^(@)`, the intensity of transmitted light decreased by a factor of `eta = 3.0`. Find the degree of polarization of incident light.
05:02View SolutionTwo identical imperfect polarizers are placed in the way of a natural beam of light. When the polarizers' planes are parallel, the system transmits `eta = 10.0` times more than in the case of crossed planes. Find the dergee of polarization of light produced
(a) by each polarizer separately,
(b) by the whole system when the planes of the polarizers are parallel.View SolutionTwo parallel plane-polarized beams of light of equal intesity whose oscillation planes `N_(1)` and `N_(2)` from a small angle `varphi` between them (Fig.) fall on a Nicol prism. To equalize the intensities of the beams emerging behind the prism, its principle direction `N` must be aligned along the bisecting line `A` or `B`. find the value of the angle `varphi` at which the rotation of the Nicol prism through a small angle `delta varphi lt lt varphi` from the position `A` results in the fractional change of intensities of the beams `DeltaI//I` by the value `eta = 100` times exceeding that resulting due to rotation through the same angle from the position `B`.
 View Solution
View SolutionResorting to the Fresnel equations, demonstrate that light reflected from the surface of dielectric will be totally polarized if the angle of incidence `theta_(1)` satisfies the condition `tan theta_(1) = n`, where `n` is the refractive index of the dielectric. What is in this case the angle between the reflected and refracted rays?
06:03View SolutionNatural light falls at the Brewster angle on the surfcae of glass. Using the Fresnel equations, find
(a) the reflection coefficient,
(b) the degree of polarization of refracted light.View SolutionA plane beam of natural light with intensity `I_(0)` falls on the surface of water at the Brewster angle. A fraction `rho = 0.039` of luminous flux is reflected. Find the intensity of the refracted beam.
06:03View SolutionA beam of plane-polarized light falls on the surface of water at the Brewster angle. The polarization plane of the electric vector of the electromagnetic wave makes an angle `varphi = 45^(@)` with the incidence plane. Find the reflection coefficient.
08:17View SolutionA narrow beam of natural light falls on the surface of a thick transparent plane-parallel plate at the Brewster angle. Its top surface. Find the degree of polarization of beams `1-4` (Fig.)
 View Solution
View SolutionA plane beam of natural light with intensity `I_(0)` falls on the surface of water at the Brewster angle. A fraction `rho = 0.039` of luminous flux is reflected. Find the intensity of the refracted beam.
06:03View SolutionA narrow beam of natural light falls on a set of `N` thick plane-parallel glass plates at the Brewster angle. Find:
(a) the degree `P` of polarization of the transmitted beam,
(b) what `P` is equal to when `N = 1, 2, 5,` and 10.03:47View SolutionUsing the Fresnel equations, find:
(a) the reflection coefficient of natural light falling normally on the surface of glass,
(b) the relative loss of luminous flux due to reflections of a paraxial ray of natural light passing through an aligned aoptical system comprising five glass lenses (secondary reflections o flight are to be neglected).View SolutionA light wave falls normally on the surface of glass coated with a layer of transparent substance. Neglecting secondary reflections, demonstrate that the amplitudes of light waves reflected from the two surfaces of such a laver will be equal under the condition `n' = sqrt(n)`, where `n'` and `n` are the refractive indiced of the layer and the glass respectively.
View SolutionA beam of natural light falls on the surface of glass at an angle of `45^(@)`. Using the Fresnel equations, find the degree of polarization of
(a) reflected light,
(b) refracted light.08:55View SolutionUsing Huygens's principle, construct the wavefronts and the propegation directions of the ordinary and extraordinary rays in a positive uniaxial crystal whose optical axis
(a) is perpendicualr to the incidence plane and parallel to the surfcae of the crystal,
(b) lies in the incidence plane and is parallel to the surface of the crystal,
(c ) lies in the incidence plane at an angle of `45^(@)` to the surface of the crystal, and light falls at right angles to the optical axis.View SolutionA narrow beam of natural light with wavelength `lambda = 589nm` falls normally on the surface of a Wollaston polarizing prism made of Iceland spar as shown in Fig. The optical axes of the two parts of the prism are mutually perpendicualr. Find the angle `delta` between the directions of the beams behind the prism if the angle `theta` is equal to `30^(@)`.
 View Solution
View SolutionWhat kind of polarizations has a plane electromagetic wave if the projections of the vector `E` on the `x` and `y` axes are perpendicular to the propagation direction and are defind by the following equations:
(a) `E_(x) = Ecos (omegat - kz), E_(y) = E sin (omegat - kz)`,
(b) `E_(x) = E cos(omegat - kz), E_(y) = E cos (omegat - kz + pi//4)`
(c) `E_(x) = E cos (omega t - kz), E_(y) = E cos (omega t - kz + pi)`?View SolutionOne has to manufacture a quartz plate cur parallel to its optical axis and not exceeding `0.50mm` is thickness. Find the maximum thickness of the plate allowing plane-polarized light with wavelength `lambda = 589 nm`
(a) to experience only rotation of polarization plane,
(b) to acquire circular polarization after passing through that plane.09:19View SolutionA quartz plate cur parallel to the optical axis placed between two crossed Nicol prisms. The angle between the principal directions of the Nicol prism and the plate is equal to `45^(@)`. The thckness of the plate is `d = 0.50mm`. At what wavelengths in the interval from `0.50` to `0.60 mu m` is the intensity of light which passed through that system independent of rotation of the rear prism? The difference of refractive indices for ordinary and extraordinary rays in that wavelength interval is assumed to be `Deltan = 0.0090`.
View SolutionWhite natural light falls on a system of two crossed Nicol prisms having between them a quartz plate `1.50 mm` thick, cut parallel to the optical axis. The axis of the plate froms an angle of `45^(@` with the principle directions of the Nicol prism. The light transmitted through that system was split into the spectrum. How many dark fringes will be observed in the wavelength interval from `0.55` to `0.66mu m`? The difference of refractve indices for ordinary and extraordianry rays in that wavelength interval is assumed to be equal to `0.0090`.
View SolutionA crystalline plate cut parallel to its optical axis is `0.25mm` thick and serves as a quarter-wave plate for a wavelength`lambda = 530nm`. At what other wavelength of visible spectrum will it also serve as a quarter-wave plate? The difference of refractive indices for extraordinary and ordianry rays is assumed to the constant and equal to `n_(e) - n_(0) = 0.0090` at all wavelength of the visible spectrum.
03:25View SolutionA quartz plate cut parallel to its optical axis is placed between two corssed Nicol prisms so that principle directions form an angle of `45^(@)` with the optical axis of the plate. What is the minimum thickness of that plate transmitting light of wavelength `lambda = 643nm` with maximum intensity while greatly reducing the intensity of transmitting light of wavelength `lambda_(2) = 564 nm`? The difference of refractive indieces indices for extroardianry and ordinary rays is assumed to be equal to `n_(e) - n_(0) = 0.0090` for both wavelengths.
05:42View SolutionA quartz wedge with refracting angle `Theta = 3.5` is inserted between two crossed Polaroids. The optical axis of the wedge is parallel to its edge and forms an angle of `45^(@)` with the principal directions of the Polaroids. On transmittion of light with wavelength `lambda = 550 nm` through this system, an interference fringe pattern is formed. The width of each fringe is `Deltax = 1.0 mm`. Find teh difference of refractive indices of quartz for ordinary and extraodianry rays at the wavelength indicated above.
View SolutionNatural monochromatic light of intensity `I_(0)` falls on a system of two Polaroids between which a crystalline plate is inserted,cut parallel to its optical axis. The plate introduces a phase difference `delta` between the ordinary and extraodianry rays. demonstrate that the intensity of light transmitted through that sysytem is equal to
`I = (1)/(2)I_(0)[cos^(2)(varphi - varphi') - sin 2varphi. sin 2varphi' sin^(2)(delta//2)]`,
where `varphi` and `varphi'` are the angles between the optical axis of the crystal and the principle directions of the Polaroids. In particular, consider the cases of crossed and parallel Polaroids.View SolutionMonochromatic light with circular polarization falls normally on a crystalline plate cut parallel to the optical axis. Behind the plate there is a Nicol prism whose principle direction froms an angle `varphi` with the optical axis of the plate. Demonsrate that the intensity of light transmitted through that system is equal to
`I = I_(0) (1 + sin2varphi. sin delta)`,
where `delta` is the phase difference between the ordianry and extraordinary rays which is introduced by the plate.05:08View SolutionExplain how, using a Polaroid and a quarter-wave plate made of positive uniaxial crystal `(n_(e) gt n_(0))`, yo distinguish
(a) light with left-hand circualr polarization from that with right-hand polarization,
(b) natural light from light with circualr polarization and from the compoitive of natural light and that with circular polarization.View SolutionLight with wavelength `lambda` falls on a system of crossed polarizer `P` and analyzer `A` between which a Babinet compesator `C` is inserted (Fig.). The compensator consists of two q2uartz wedges with the optical axis of one of them being parallel to the edge, and of the other, perpendicular to it. The principal directions of the polarizer and the analyser from an angle of `45^(@)` with the optical axes of the compensator. The refracting angle of the wedges is equal to `Theta(Theta lt lt 1)` qand the difference of refractive indices of quartz is `n_(e) - n_(0)`. The insertion of investigated birefringent sample `S`, with the optical axis oriented as shown in the figure, results in displacement of the fringe upward by `deltax mm`. Find:
the width of the fringe `Deltax`,
(b) the magnitude and the sign of the optical path difference of ordinary and extraordianry rays, which appears due to the sample `S`.
 View Solution
View SolutionUsing the tables of the Appendix, calculate the difference of refractive indices of quartz for light wavelength `lambda = 589.5 nm` with right-hand and left-hand circular polarizations.
01:51View SolutionPlane-polarized light of wavelength `0.59mu m` falls on a trihedral quartz prism `P` (Fig.) with refracting angle `Theta = 30^(@)`. Inside the prism light propagates along the optical axis whose direction is shwon by hatching. Behind the Polaroid Pol an interference pattern of bright and dark fringes of width `Deltax = 15.0mm` is pbserved. Find the specific rotation constant of quartz and the distribution of intensity of light behind the Polaroid.
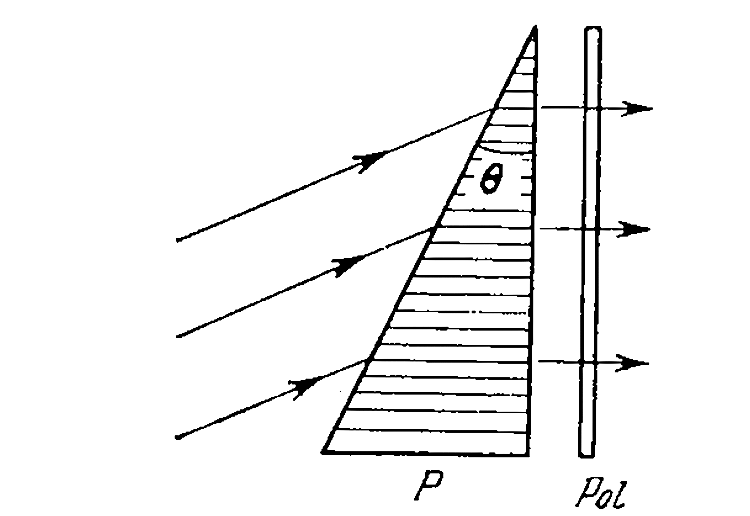 View Solution
View SolutionNatural monochromatic light falls on a system of two crossed Nicol prisms between to its optical axis is insered. Find the minimum thickness of the plate at which this system will transmit `eta = 0.30` of luuminous flux if the specific rotation constant of quartz is equal to `alpha = 17 ang deg// mm`.
04:22View SolutionLight passes through a system of two crossed Nicol prisms between which a quartz plate cut at right angles to its optical axis is placed. Determine the minimum thickness of the plate which allows light of wavelength `436 nm` to be complately cut off by the system and transmits half the light of wavelength `497 nm`. The specific rotation constant of quartz for these wavelength is equal to `41.5` and `31.1` angualr degress per mm respectively.
04:08View SolutionPlane-polarized light of wavelength `589nm` propagates along the axis of a concentration `500 g//l`. Viewing from the side, one can see a system of helical fringes, with `50 cm` between neighbouring dark fringes along the axis. Explain the emergence of the fringes and determine the specific rotation consatnt of the solution.
View SolutionA Kerr cell is positioned between two crossed Nicol prisms so that the direction of electric field `E` in the capacitor forms an angle of `45^(@)` with the principle directions of the prisms. The capacitor has the length `l = 10 cm` and is falled up with nitrobenzence. Light of wavelength `lambda = 0.50 mu m` passes through the system. Taking into account that in this case the kerr constant is equal to `B = 2.2.10^(-10)cm//V^(2)`, find:
(a) the minimum strength of electric field `E` in the capacitor at which the intensity of light that passes through this syetm is independent of rotation of the rear prism,
(b) how many times per second light will be interrupted when a sinusoidal voltage of frequecny `v = 10 MHz` and strength amplitude `E_(m) = 50kV//cm` is applied to the capacitor.
Note. The Kerr constant is the coefficient `B` in the equation `n_(e) = n_(0) = Blambda E^(2)`.View SolutionMonochromatic plane-polarized light with angular frequency `omega` through a certain substance along a unifrom magnetic field `h`. Find the difference of refractive indices for right-hand and left-hand components of light beam with circular polarization if the verdet consatnt is equal to `V`.
02:34View SolutionA certain substance is placed in a longitudinal magnetic field of a solenoid located between two Polaroids. The length of the tube wity substance is equal to `l = 30 cm`. Find the verdet constant if at a field strength `H = 56.5 kA//m`, the angle of rotation of polarization plane is equal to `varphi_(1) =+ 5^(@) 10`' for one direction of the field and to `varphi_(2) =- 3^(@) 20`,' for the opposite direction.
04:03View SolutionA narrow beam of plane-polarized light passes through dextrorotatory positive compound placed into a longitudinal magnetic field as shown in Fig. Find the angle through which the polarization plane of the transmitted beam will turn if the length of the tube with the componed is equal to `l`, the specific rotation constant of the compound is equal to `alpha`, the verder constant is `V`, and the magnetic field strength is `H`.
 View Solution
View SolutionA tube of length `l = 26 cm` is filled with benzence and placed in a longitudinal magnetic field of a solenoid positioned between two Polaroids. The angle between the principle directions of the Polaroids is equal to `45^(@)`. Find the minimum strength of the magnetic field at which light of the wavelength `589 nm` propagates through that system only in one direction (optical value). What happens if teh idrection of the given magnetic field is changed to the opposite one?
02:57View SolutionExperience shows that a body irradiated with light with circular polarization acquires a torque. This happens because such a light possesses an angular momentum whose flow density in vacuum is equal to `M = I//omega`, where `I` is the intensity o flight, `omega` is the angualr oscillation frequacny. Suppose light with circualr polarization and wavelength `lambda = 0.70 mu m` falls normally on a uniform black disc of mass `m = 10 mg` which can freely rotate about its axis. How soon will its angualr velocity become equal to `omega_(0) = 1.0 rad//s` provided `I = 10 W//cm^(2)`?
04:58View Solution
Polarization Of Light questions and complete solutions for chapter OPTICS of IE IRODOV PHYSICS (HINGLISH) of Class 12
