Complete Solutions to Exercise of chapter CORDINATES AND STARIGHT LINES - FOR COMPETITION of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | CORDINATES AND STARIGHT LINES - FOR COMPETITION |
| KC SINHA | Exercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Let the opposite angular points of a square be `(3,4)a n d(1,-1)` . Find the coordinates of the remaining angular points.
View SolutionA(-4,0) and B (-1,4) are two given points. Cand D are points which are symmetric to the given points A and B respectively with respect to y-axis. Calculate the perimeter of the trapezium ABDC.
View SolutionIf the point A is symmetric to the point `B(4,-1)` with respect to the bisector of the first quadrant, then the length of AB is:
View SolutionA line through the point `A(2, 0)` which makes an angle of `30^0` with the positive direction of x-axis is rotated about `A` in clockwise direction through an angle `15^0`. Find the equation of the straight line in the new position.
View SolutionThe point `(1, -2)` is reflected in the x-axis and then translated parallel to the positive direction of x-axis through a distance of 3 units, find the coordinates of the point in the new position.
View SolutionThe line segment joining `A(3, 0) and B(5, 2)` is rotated about `A` in the anticlockwise direction through an angle of `45^0` so that `B` goes to `C`. If `D` is the reflection of `C` in y-axis, find the coordinates of `D`.
View SolutionTwo vertices of a triangle are `A(2, 1) and B (3, -2)`. The third vertex `C` lies on the line `y=x+9`. If the centroid of `DeltaABC` lies on y-axis, find the coordinates of `C` and the centroid.
View SolutionIf `a ,b ,c` are the `p t h ,q t h ,r t h` terms, respectively, of an `H P` , show that the points `(b c ,p),(c a ,q),` and `(a b ,r)` are collinear.
View SolutionThe area of a triangle is `3/2` square units. Two of its vertices are the points `A (2, -3)` and `B(3,-2)`, the third vertex of the triangle lies on the line `3x - y -2 = 0`, then third vertex C is
View SolutionProve that the quadrilateral whose vertices are `A (-2, 5), B (4, -1), C (9, 1) and D(3, 7)` is a parallelogram and find its area. If E divides AC in the ration `2:1`, prove that D, E and the middle point F of BC are collinear.
View SolutionA line through the point `A(2, 0)` which makes an angle of `30^0` with the positive direction of x-axis is rotated about `A` in clockwise direction through an angle `15^0`. Find the equation of the straight line in the new position.
View SolutionA line through the point `P (1, 2)` makes an angle of `60^0` with the positive directin of `x-axis` and is rotated about `P` in the clockwise direction through an angle `15^0`. Find the equation of the straight line in the new position.
View SolutionThe line `2x-y = 5` turns about the point on it, whose ordinate and abscissae are equal through an angle of `45^@` in the anti-clockwise direction. Find the equation of the line in the new position.
View SolutionThe line `x+ 2y=4` is-translated parallel to itself by `3` units in the sense of increasing x and is then rotated by `30^@` in the clockwise direction about the point where the shifted line cuts the x-axis.Find the equation of the line in the new position
View Solution`AB` is a side of a regular hexagon `ABCDEF ` and is of length `a` with `A` as the origin and `AB` and `AE` as the x-axis andy-axis respectively. Find the equation of lines `AC, AF` and `BE`
View SolutionA straight road is at a distance of `5sqrt(2)` miles from a place. The shortest distance of the road from the place is in the N.E. direction. Do the following villages which (i) is 6 miles East and 4 miles North from the place lie on the road or no, (ii) is 4 miles East and 3 miles North from the place, lie on the road or not?
View SolutionIn the given figure, PQR is an euilateral triangle and OSPT is a square. If OT `=2sqrt(2)` units, find the equation of lines OT, OS, SP, QR, PR, and PQ.
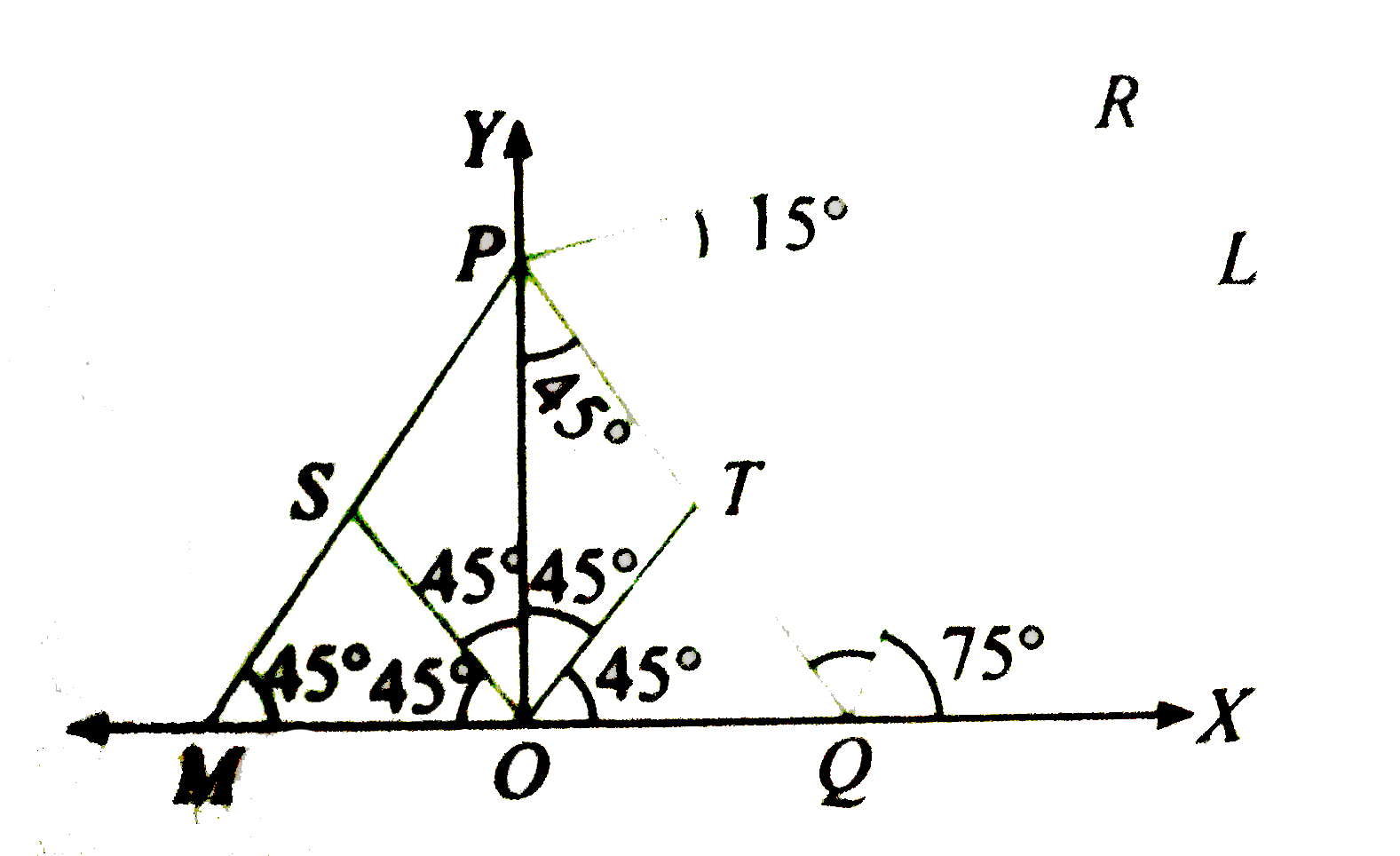
View SolutionTwo particles start from the point (2,-1), one moves 2 units along the line x+y = 1 and the other moves 5 units along the line x-2y = 4. If the particles move upward w.r.t coordinates axes, then find their new positions.
View SolutionOne end of a thin straight elastic string is fixed at `A(4,-1)` and the other end `B` is at `(1,2)` in the unstretched condition. If the string is stretched to triple its length to the point `C ,` then find the coordinates of this point.
View SolutionThe line PQ whose equation is x-y = 2 cuts the x-axis at P, and Q is (4,2). The line PQ is rotated about P through `45^(@)` in the anticlockwise direction. The equation of the line PQ in the new position is
View SolutionThe extremities of a diagonal of a squaer are `(1, 1), (-2, -1)`. Obtain the other two vertices and the equation of the other diagonal.
View SolutionThe straight line passing through `P(x_1,y_1)` and making an angle `alpha` with x-axis intersects `Ax + By + C=0` in Q then `PQ` =________________
View SolutionA line which the positive direction of x-axis is drawn through the point `P(3, 4),` to cut the curve `y^2= 4x` at `Q ` and `R`. Show that the lengths of the segments `PQ` and `PR` are numerical values of the roots of the equation `r^2sin^2theta+4r(2sintheta-costheta)+4=0`
View SolutionThe lines `2x+3y+19=0` and `9x+6y-17=0` , cut the coordinate axes at concyclic points.
View SolutionA straight line `L` is perpendicular to the line `5x-y=1` . The area of the triangle formed by line `L ,` and the coordinate axes is 5. Find the equation of line `Ldot`
View SolutionThe line `2x+3y=12` meets the x-axis at A and y-axis at B. The line through (5,5) perpendicular to AB meets the x-axis and the line AB at C and E respectively. If O is the origin of coordinates, find the area of figure OCEB.
View Solutionabout to only mathematics
View SolutionA light beam, emanating from the point (3,10) reflects from the straight line `2x+y - 6 = 0` and, then passes through the point (7,2) .Find the equations of the incident and reflected beams .
View SolutionLet ` A -= (3, 2) ` and ` B-= (5, 1) ` . ABP is an equilateral triangle is constructed one the side of AB remote from the origin then the orthocentre of triangle ABP is :
View SolutionThe vertices of a triangle are `A(x_1, x_1tantheta_1),B(x_2, x_2tantheta_2)a n dC(x_3, x_3tantheta_3)dot` if the circumcentre of `"Delta"A B C` coincides with the origin and `H( x , y )` is the orthocentre, show that ` y/( x )=(sintheta_1+s intheta_2+sintheta_3)/(costheta_1+costheta_2+costheta_3)`
View SolutionThe circumcentre of a triangle with vertices `(a, a tan alpha), B(b, b tan beta)` and `C (c, c tan gamma)` lies at the origin, where `0 lt alpha beta, gamma lt pi//2` and `a+ beta+gamma = pi`. Show that its orthocentre lies on the line `4 cos((alpha)/(2))cos((beta)/(2))cos((gamma)/(2))x - 4 sin ((alpha)/(2))sin((beta)/(2))sin((gamma)/(2))y=y`
View SolutionDetermine whether the origin lies inside or outside the triangle whose sides are given by the equations `7x-5y-11=0, 8x+3y+31=0, x+8y-19=0`.
View SolutionThe equations of two sides of a square are `3x+4y-5=0 and 3x+4y-15=0`. The third side has a point (6, 5) on it. Find the equation of this third side and the remaining side of the square.
View SolutionShow that the reflection of the line `px+qy+r=0` in the line `x+y+1 =0` is the line `qx+py+(p+q-r)=0,` where `p!= -q`.
View SolutionA rhombus has two of its sides parallel to the lines `y=2x+3 and y=7x+2`. If the diagonals cut at (1, 2) and one vertex is on the y-axis, find the possible values of the coordinate of that vertex.
View Solutionif `x` and `y` coordinates of a point `P` in `x-y `plane are given by `x=(ucosalpha)t, y=(usinalpha )t-1/2 g t^2 `where `t` is a aprameter and `u,alpha,g`the constants. Then the locus of the point `P` is a parabola then whose vertex is:
View SolutionA variable line through the point `((6)/(5),(6)/(5))` cuts the coordinate axes at the points A and B respectively. If the point P divides AB internally in the ratio `2:1`, then the equation of the locus of P is
View SolutionA straight line moves in such a way that the length of the perpendicular upon it from the origin is always `p`. Find the locus of the centroid of the triangle which is formed by the line and the axes.
View SolutionA right angled triangle ABC having a right angle at C, CA=b and CB=a, move such that angular points A and B slide along x-axis and y-axis respectively. Find the locus of C
View SolutionThe vertices of a triangle ABC are the points `(0, b), (-a, 0), (a, 0)`. Find the locus of a point `P` which moves inside the triangle such that the product of perpendiculars from `P` to `AB and AC` is equal to the square of the perpendicular to `BC`.
View SolutionFind the locus of the point at which two given portions of the straight line subtend equal angle.
View SolutionA point is moving in such a way that sum of the squares of perpendiculars drawn from it to the sides of an equilaeral triangle is constant. Prove that its locus is a circle.
View SolutionFind the locus of the middle points of the segment of a line passing through the point of intersection of lines `ax + by + c = 0 and lx + my + n = 0` and intercepted between the axes.
View SolutionA point `P` move along the y-axis. Another point `Q` moves so that the fixed straight line `x cos alpha +y sin alpha = p` is the perpendicular bisector of the line segment `PQ`.Find the locus of `Q`.
View SolutionThe vertices `Ba n dC` of a triangle `A B C` lie on the lines `3y=4xa n dy=0` , respectively, and the side `B C` passes through the point `(2/3,2/3)` . If `A B O C` is a rhombus lying in the first quadrant, `O` being the origin, find the equation of the line `B Cdot`
View Solution`ABC` is a right angled triangle, right-angled at `A`. The coordinates of `B and C` are (6, 4) and ((14, 10) respectively. The angle between the side AB and x-axis is `45^0`. Find the coordinates of `A`.
View SolutionThe line joining `A(bcosalpha,bsinalpha)` and `B(acosbeta,asinbeta)` is produced to the point `M(x ,y)` so that `A M` and `B M` are in the ratio `b : adot` Then prove that `x+ytan((alpha+beta)/2)=0.`
View SolutionThe equation of the side AB and AC of a triangle ABC are `3x+4y+9` and `4x-3y+16=0` respectively. The third side passes through the point `D(5, 2)` such that `BD:DC=4:5`. Find the equation of the third side.
View SolutionLet n be the number of points having rational coordinates at a fixed distance fromt the point `(0,sqrt3)`. Then
View SolutionIf poitns `A(3,5)` and B are equidistant from `H(sqrt2,sqrt5)` and B has rational coordinates,then `AB=`
View SolutionFind the number of point `(x ,y)` having integral coordinates satisfying the condition `x^2+y^2<25`
View SolutionABC is an equilateral triangle such that the vertices B and C lie on two parallel lines at a distance 6. If A lies between the parallel lines at a distance 4 from one of them, then the length of a side of the equilatereal triangle is
View SolutionIf all the vertices of a triangle have integral coordinates, then the triangle may be (a) right-angle (b) equilateral (c) isosceles (d) none of these
View SolutionLet `A-=(-4, 0), B -= (-1, 4). C and D` are points which are symmetric to points `A and B` respectively with respect to y-axis, then area of the quadrilateral `ABCD` is (A) 8 sq units (B) 12 sq. units (C) 20 sq. units (D) none of these
View SolutionIf `x_1,x_2,x_3` as well as `y_1, y_2, y_3` are in G.P. with same common ratio, then prove that the points `(x_1, y_1),(x_2,y_2),a n d(x_3, y_3)` are collinear.
View SolutionIf `x_1,x_2,x_3` as well as `y_1,y_2,y_3` are in `G P` with the same common ratio, then the points `(x_1,y_1),(x_2,y_2),` and `(x_3, y_3)dot` (a)lie on a straight line (b)lie on an ellipse (c)lie on a circle (d) are the vertices of a triangle.
View Solution`P(3,1),Q(6,5)` and `R(x,y)` are three points such that `PRQ` is a right angle and the area of `DeltaRQP` is 7 sq.unit. Find the number of such points R.
View SolutionLet `alpha = Lt_(mrarroo) Lt_(nrarroo) cos^(2m) |__n pix`, where `x` is rational, `beta= Lt_(mrarroo) Lt_(nrarroo) cos^(2m) |__n pix,` where \'x\' is irrational, then the area of the triangle having vertices `(alpha, beta), (-2, 1) and (2, 1)` is (A) 2 (B) 4 (C) 1 (D) none of these
View SolutionThe incenter of the triangle with vertices `(1,sqrt(3)),(0,0),` and `(2,0)` is `(1,(sqrt(3))/2)` (b) `(2/3,1/(sqrt(3)))` `(2/3,(sqrt(3))/2)` (d) `(1,1/(sqrt(3)))`
View SolutionIf `P(1,2)Q(4,6),R(5,7),` and `S(a , b)` are the vertices of a parallelogram `P Q R S ,` then (a)`a=2,b=4` (b) `a=3,b=4` (c)`a=2,b=3` (d) `a=1,b=-1`
View SolutionIf a point `P` moves such that the sum of its distances from two perpendicular lines is less than or equal to 2 and `S` be the region consisting of all such points `P`, then area of the region `S` is : (A) 4 sq.untis (B) 8 sq. units (C) 6 sq. units (D) none of these
View Solutionabout to only mathematics
View SolutionIf the algebraic sum of the perpendicular distances from the points `(3, 1), (-1, 2) and (1, 3)` to a variable line be zero, and `|(x^2+1, x+1, x+2), (2x+3, 3x+2, x+4), (x+4, 4x+3, 2x+5)|= mx^4 + nx^3 + px^2 + qx+r` be an identity in `x`, then the variable line always passes through the point (A) `(-r, m)` (B) `(-m, r)` (C) `(r, m)` (D) `(2r, m)`
View SolutionA man starts from the point `P(-3,4)` and reaches point `Q(0,1)` touching X - axis at R such that `PR+RQ` is minimum , then the point R is
View SolutionLet `P-= (a,b), Q-=(c, d) and 0ltaltbltcltd, L-=(a,0), M-=(c, 0), R` lies on x-axis such that `PR=RQ` is minimum, then `R` divides `LM` (A) internally in the ration `a:b` (B) internally in the ration `b:c` (C) internally in the ration `b:d` (D) internally in the ratio `d:b`
View SolutionIf `a= (tan theta)/(tan 3theta)`, then the point `P(a, a^2)` (A) necessarily lies in the acute angle between the lines `y=3x and 3y=x` (B) may lie on line `3y=x` or `y=3x` (C) necessarily lies in the obtuse angle between the lines `3y=x` and `y=3x` (D) `aepsilon (1/3, 3)`
View SolutionIf `alpha` an integer and `P (alpha, alpha^2)` is a point in the interior of the quadrilateral `x=0, y=0, 4x+y-21=0 and 3x+y-4=0, and (1+ax)^n = 1 + 8x+24x^2 + …,` then `alpha=` (A) `a` (B) `-a` (C) `a^2` (D) none of these
View SolutionIf `a, b, c` are variables such that `21a + 40b + 56c=0` then the family of lines `ax+by+c=0` passes through (A) `(7/14, 9/4)` (B) `(4/7, 3/8)` (C) `(3/8, 5/7)` (D) `(2, 3)`
View SolutionConsider a triangle `PQR` with `P-= (0, 0), Q-= (a, 0), R -=(0, b)`. Then the centroid, orthocentre and circumcentre (A) lies on a straight line (B) form a scalene triangle with area `a/2 |ab|` (C) form a right-angled triangle with area `1/2 |ab|` (D) none of these
View SolutionThe equaiton of the line which bisects the obtuse angle between the lines `x-2y+4=0 and 4x-3y+2=0` (A) `(4-sqrt(5))x-(3-2(sqrt(5)) y+ (2-4sqrt(5))=0` (B) `(3-2sqrt(5)) x- (4-sqrt(5))y+ (2+4(sqrt(5))=0` (C) `(4+sqrt(5)x-(3+2(sqrt(5))y+ (2+4(sqrt(5))=0` (D) none of these
View SolutionIf two sides of a triangle are represented by `2x-3y+4=0 and 3x+2y-3=0`, then its orthocentre lies on the line : (A) `x-y+ 8/15 = 0` (B) `3x-2y+1=0` (C) `9x-y+9/13 = 0` (D) `4x+3y+5/13=0`
View SolutionEquation of the line equidistant from `3x+4y-25=0 and 3x+4y+25=0` is
(A) `6x+4y+5=0` (B) `3x+4y=0` (C) `3x-4y+5=0` (D) `6x+8y+5=0`
View SolutionThe equation of a line through `(2, -4)` which cuts the axes so that the intercepts are equal in magnitude is :
(A) `x+y+2=0` (B) `x-y+2=0` (C) `x+y+6=0` (D) `x+y-6=0`
View SolutionIf a line is perpendicular to the line `5x-y=0` and forms a triangle with coordinate axes of area 5 sq. units, then its equation is :
View SolutionFind the equation of a straight line through the intersection of `2x -3y + 4 =0` and `3x+ 4y- 5 =0` and parallel to `Y` -axis
View SolutionA variable line intersects the co-ordinate axes at A and B and passes through a fixed point `(a, b)`.then the locus of the vertex C of the rectangle `OACB` where O is the origin is
View SolutionThe family of lines `(l+3m) x + 2(l+m) y= (m-l)`, where `l!=0` passes through a fixed point having coordinates (A) `(2, -1)` (B) (0, 1) (C) `(1, -1)` (D) `(2, 3)`
View SolutionThe equation of the line passing through (1,2) and having a distance equal to 7 units from the points (8,9) is
View SolutionIf `a ,\ b , c` are in A.P., then the line `a x+b y+c=0` passes through a fixed point. write the coordinates of that point.
View SolutionThe coordinates of the vertices A and B of an isosceles triangle `ABC (AC=BC)` are `(-2, 3) and (2, 0)` respectively. A line parallel to AB and having a y-intercept equal to `43/12` passes through `C`, then the coordinatse of `C` are : (A) `(- 3/4, 1)` (B) `(1, 17/6)` (C) `(2/3, 4/5)` (D) `(1, 0)`
View SolutionThe equaiton of the line perpendicular to `2x+6y+5=0` and having the length of x-intercept equal to 3 units can be (A) `y=3x+5` (B) `2y=6x+1` (C) `y=3x+9` (D) none of these
View SolutionThe point on the line `3x-2y=1` which is closest to the origin is
(A) `(3/13, - 2/13)` (B) `(5/11, 2/11)` (C) `(3/5, 2/5)` (D) none of these
View SolutionVerify the following: (5,-1,1),(7,-4,7), (1,-6,10) and (-1,-3,4) are the vertices of a rhombus.
View SolutionFind the distance of the point (2,5) from the line `3x+y+4=0` measured parallel to the line `3x-4y+8=0`
View SolutionIf `A(-1, 0), B(1, 0) and C(3, 0)` are three given points, then the locus of point `D` satisfying the relation `DA^2 + DB^2 = 2DC^2` is (A) a straight line parallel to x-axis (B) a striaght line parallel to y-axis (C) a circle (D) none of these
View SolutionA point (1, 1) undergoes reflection in the x-axis and then the coordinates axes are rotated through an angle of `pi/4` in anticlockwise direction. The final position of the point in the new coordinate system is
View SolutionIf the point `(1, a)` lies in between the lines `x + y =1` and `2(x+y) = 3` then `a` lies in
(i)`(-infty,0)cup (1,infty)` (ii)`(0,1/2)` (iii)`(-infty,0)cup (1/2,infty)` (iv) none of these
View Solution`A=(sqrt(1-t^2)+t, 0)` and `B=(sqrt(1-t^2)-t, 2t)` are two variable points then the locus of mid-point of `AB` is
View SolutionThe equation of a straight line passing through (3, 2) and cutting an intercept of 2 units between the lines `3x+4y=11 and 3x+4y=1` is (A) `2x+y-8=0` (B) `3y-4x+6=0` (C) `3x+4y-17=0` (D) `2x-y-4=0`
View SolutionThe coordinates of the foot of perpendicular drawn from the point (2, 4) on the line `x+y=1` are (A) `(1/2, 1/2)` (B) `(- 1/2, 3/2)` (C) `(1/4, 3/4)` (D) `(3/2, - 1/2)`
View SolutionThe equation of straight line equally inclined to the axes and equidistant from the point `(1, -2)` and `(3,4)` is:
View SolutionThe equation `sqrt(x^2 + 4y^2 - 4xy+4) +x-2y=1` represent a (A) straight line (B) circle (C) parabola (D) pair of lines
View SolutionIf a `DeltaABC` remains always similar to a given triangle and the point `A` is fixed and the point `B` always moves on a given straight line, then locus of `C` is (A) a circle (B) a straight line (C) a parabola (D) none of these
View Solutionabout to only mathematics
View SolutionA variable line through the point `(p, q)` cuts the `x and y` axes at `A and B` respectively. The lines through `A and B` parallel to y-axis and x-axis respectively meet at `P`. If the locus of `P` is `3x+2y-xy=0`, then (A) `p=2, q=3` (B) `p=3, q=2` (C) `p=2, q=-3` (D) `p=-3, q=-2`
View SolutionIf `f(x+y)=f(x)f(y) AA x, y in R` and f(1) = 2 , then area enclosed by `3|x|+2|y|le 8` is
View Solutionabout to only mathematics
View SolutionThe point `(-4,5)` is vertex of a square and one of its diagonal is `7x-y+8=0.` The equation of other diagonal is
View SolutionIf `(alpha, beta)` be the circumcentre of the triangle whose sides are `3x-y=5, x+3y=4 and 5x+3y+1=0`, then (A) `11alpha - 21beta = 0` (B) `11alpha + 21beta = 0` (C) `alpha +2beta=0` (D) none of these
View Solutionif `x/a+y/b=1` is a variable line where `1/a^2+1/b^2=1/c^2` (`c` is constant ) then the locus of foot of the perpendicular drawn from origin
View Solution
Exercise questions and complete solutions for chapter CORDINATES AND STARIGHT LINES - FOR COMPETITION of KC SINHA ENGLISH of Class 12