Complete Solutions to EXAMPLE of chapter APPLICATION OF DERIVATIVES of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | APPLICATION OF DERIVATIVES |
| MAXIMUM PUBLICATION | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Find the equation of tangents and normals to the given curves `x=cost,y=sint,` at `t=pi/4`
View SolutionA ladder 5m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2cm/s. How fast is its height on the decreasing when the foot of the ladder is 4m away from the wall.
View SolutionFind the points on the curve `y=x^3`, the tangents at which are inclined at an angle of 60° to x-axis?
View SolutionFind the equation of the tangent to the parabola
`y^2=4x+5` which is parallel to `y=2x+7`.
View SolutionFind the intervals in which the function `f` given `f(x)=2x^2-3x` is
Strictly Increasing.
View SolutionFind the intervals in which the function `f` given `f(x)=2x^2-3x` is
Strictly Decreasing.
View SolutionFind the intervals in which the function `f(x)=(x+1)^3(x-3)^3` strictly increasing or decreasing.
View SolutionFind the intervals in which the function
`f(x)=x+1/x` strictly increasing or decreasing.
View SolutionDetermine whether the `f(x)=x^2` function is strictly monotonic on the indicated interval.
`(-1,1)`
View SolutionDetermine whether the `f(x)=x^2` function is strictly monotonic on the indicated interval.
`(-1,0)`
View SolutionDetermine whether the `f(x)=x^2` function is strictly monotonic on the indicated interval.
`(0,1)`
View SolutionDetermine whether the `f(x)=x^3-x` function is strictly monotonic on the indicated interval.
`(-1,0)`
View SolutionDetermine whether the `f(x)=x^3-x` function is strictly monotonic on the indicated interval.
`(-1,(-1)/2)`
View SolutionDetermine whether the `f(x)=x^3-x` function is strictly monotonic on the indicated interval.
`(-1,1)`
View SolutionFind the approximate change in the volume V of a cube of side x meters caused by increasing the side by 1%.
View SolutionIf the radious of a sphere is measured as 7m with an error of 0.02m then find the approximate error in calculating its volume.
View SolutionThe length of a rectangle is decreasing at the rate of 5 cm/mi and the width is increasing at the rate of 4cm/min.When length is 8 cm and width is 6 cm, find the rate of change of its area.
View SolutionFind the equation on tangents and normals to the given curves
`y=x^4-6x^3+13x^2-10x+5` at `(0,5)`
View SolutionFind the equation of tangents and normals to the given curves `y=x^3` at `(1,1)`
View SolutionThe volume of a cube is increasing at the rate of `8cm^3//S`. How fast is the surface area increasing when the length of an edge is 12cm.
View SolutionFind the intervals in which the function `f(x)=-2x^3-9x^2-12x+1` strictly increasing or decreasing.
View SolutionFind the local maxima and minima of the following functions. Also find the local maximum and minimum values.
`f(x)=sinx+cosx,0ltxltpi/2`
View SolutionFind the local maxima and minima of the following functions. Also find the local maximum and minimum values.
`f(x)=x^3-3x`
View SolutionFind the local maxima and minima of the following functions. Also find the local maximum and minimum values.
`f(x)=x^3-6x^2+9x+15`
View SolutionFind the local maxima and minima of the following functions. Also find the local maximum and minimum values.
`g(x)=x/2+2/x,x>0`
View SolutionFind the local maxima and minima of the following functions. Also find the local maximum and minimum values.
`g(x)=frac(1)(x^2+2)`
View SolutionFind the absolute maximum value and minimum value of the following functions.
`f(x)=x^3, x in [-2,2]`
View SolutionFind the absolute maximum value and minimum value of the following functions.
`f(x)=4x-x^2/2, x in [-2,9/2]`
View SolutionA television camera at ground level is filming the lift-off of a space shuttle that is rising vertically according to position equation `S=50t^2`.
The camera is 2000 feet from the launch pad. Find the rate of change in the angle of elevation of the camera 10 seconds after lift-off.
View SolutionDetermine whether the `f(x)=sinx ` function is strictly monotonic on the indicated interval.
`(0,2pi)`
View SolutionDetermine whether the `f(x)=sinx ` function is strictly monotonic on the indicated interval.
`(0,pi)`
View SolutionDetermine whether the `f(x)=sinx` function is strictly monotonic on the indicated interval.
`(-pi/2, pi/2)`
View SolutionFind the approximate change in the surface area of a cube of side x meters caused by decreasing the side by 1%.
View SolutionThe length 'x' of a rectangle is decreasing at the rate of `2cm//s` and the width 'y' is increasing at the rate of `2cm//s`.
Find the rate of change of perimeter.
View SolutionThe length 'x' of a rectangle is decreasing at the rate of `2cm//s` and the width 'y' is increasing at the rate of `2cm//s`.
Find `(dA)/(dt)` when x=12 cm and y = 5 cm.
View SolutionFind the points on the curve
`x^2+y^2-2x-3=0` at which the tangent are parallel to x-axis.
View SolutionFind the equation of the tangent to the curve `y=sqrt(3x-2)` which is parallel to the line `4x-2y+5=0`.
View SolutionProve that the curve `x=y^2` and `xy=k` cut at right angles, if `8k^2=1`.
View SolutionThe gradient at any point (x,y) of a curve is `3x^2-12` and the curve through the point (2,-7).
Find the equation of the tangent at the point (2,-7).
View SolutionThe gradient at any point (x,y) of a curve is `3x^2-12` and the curve through the point (2,-7).
Find the equation to the curve.
View SolutionConsider the curve `x^(2/3)+y^(2/3)=2`
Find the slope of the tangent to the curve at the point (1,1).
View SolutionConsider the curve `x^(2/3)+y^(2/3)=2`
Find the equation of the normal at the point (1,1).
View SolutionFind the intervals in which the function `f` given by `f(x)=2x^3-3x^2-36x+7` is
Strictly Increasing.
View SolutionFind the intervals in which the function `f` given by `f(x)=2x^3-3x^2-36x+7` is
Strictly Decreasing.
View SolutionUse differentials to find the approximate value of `sqrt0.6` up to 3 places of decimals.
View SolutionUse differentials to find the approximate value of `(0.999)^(1/10)` up to 3 places of decimals.
View SolutionUse differentials to find the approximate value of `(15)^(1/4)` up to 3 places of decimals.
View SolutionUse differentials to find the approximate value of `(26.57)^(1/3)` up to 3 places of decimals.
View SolutionFind the approximate value of `f(5.001)` where `f(x)=x^3-7x^2+15`.
View SolutionFind the approximate value of `f(3.02)` where `f(x)=3x^2+5x+3`.
View SolutionConsider the function `y=sqrtx`
If `x=0.0036` and `trianglex=0.0001` find `triangley`.
View SolutionConsider the function `y=sqrtx`
Hence approximate `sqrt.0037` using differentials.
View SolutionFind the approximate value of `root(3)(124)`.
View SolutionFind two numbers x and y such that their sum is 35 and the product `x^2y^5` is a maximum.
View SolutionUsing differentials, find the approximate value of `(63)^(1/3)`
View SolutionFind the point on the curve `y=x^3-10x+8` at which the tangent is parallel to the line `y=2x+1`.
View SolutionFind the point on the curve `y=x^3-10x+8` at which the tangent is parallel to the line `y=2x+1`.Is the given line tangent to the curve? Why?
View SolutionSuppose that a spherical balloon is inflated and it has volume 'v' and radius 'r' at time 't'.
If the balloon is inflated by pumping 900c.c. of gas per second. Find the rate at which the radius of the balloon is increasing when the radious is 15 cm.
View SolutionSuppose that a spherical balloon is inflated and it has volume 'v' and radius 'r' at time 't'.
If the balloon is inflated by pumping 900c.c. of gas per second. Find the rate at which the radius of the balloon is increasing when the radious is 15 cm.
View SolutionUse differentials to find the approximate value of `(0.009)^(1/3)` up to 3 places of decimals.
View SolutionFind the approximate value of `sqrt401`.
View SolutionConsider `y=logx/x`, in `(0,infty)`
Find the value of x at which `dy/dx=0`
View SolutionConsider `y=logx/x`, in `(0,infty)`
Find the maximum value.
View SolutionFind the point on the curve `y=x^3-11x+5` at which the tangent is `y=x-11`
View SolutionConsider the curve `y=x^2-2x+7`
Find the slope of the tangent of the curve at `x=2`.
View SolutionConsider the curve `y=x^2-2x+7`
Write down the equation of the tangent at `x=2`.
View SolutionFind the absolute maximum value and minimum value of the function.
`f(x)=2x^3-15x^2+36x+1, x in [1,5]`
View SolutionFind the absolute maximum value and minimum value of the function.
`f(x)=12x^(4/3)-6x^(1/3), x in [-1,1]`
View SolutionConsider the function `y=x^3-6x^2+3x-1`
Find the slope at `x=-1`.
View SolutionConsider the function `y=x^3-6x^2+3x-1`
Find the minimum gradient of the above curve.
View SolutionA curve passes through the origin, and its gradient function is `2x-x^2/2`.
Find its y coordinate when `x=2`.
View SolutionA curve passes through the origin, and its gradient function is `2x-x^2/2`.
Find the equation of the tangent at `x=2`.
View SolutionChoose the correct answer from the bracket. The slope of the tangent to the curve `y=x^3-2x+3` at x=1 is……
View SolutionFind points on the curve `x^2/25+y^2/9=1` at which the tangents are
Parallel to x-axis.
View SolutionFind points on the curve `x^2/25+y^2/9=1` at which the tangents are
Parallel to y-axis.
View SolutionUse differential to approximate `sqrt25.6`
View SolutionLet x and y be the length and breadth of the rectangle ABCD in a circle having radius r. Let `angleCAB=theta` (Ref. Figure). If `triangle` represent area of the rectangle and r is a constant.
Write `triangle` in terms of r and `theta`.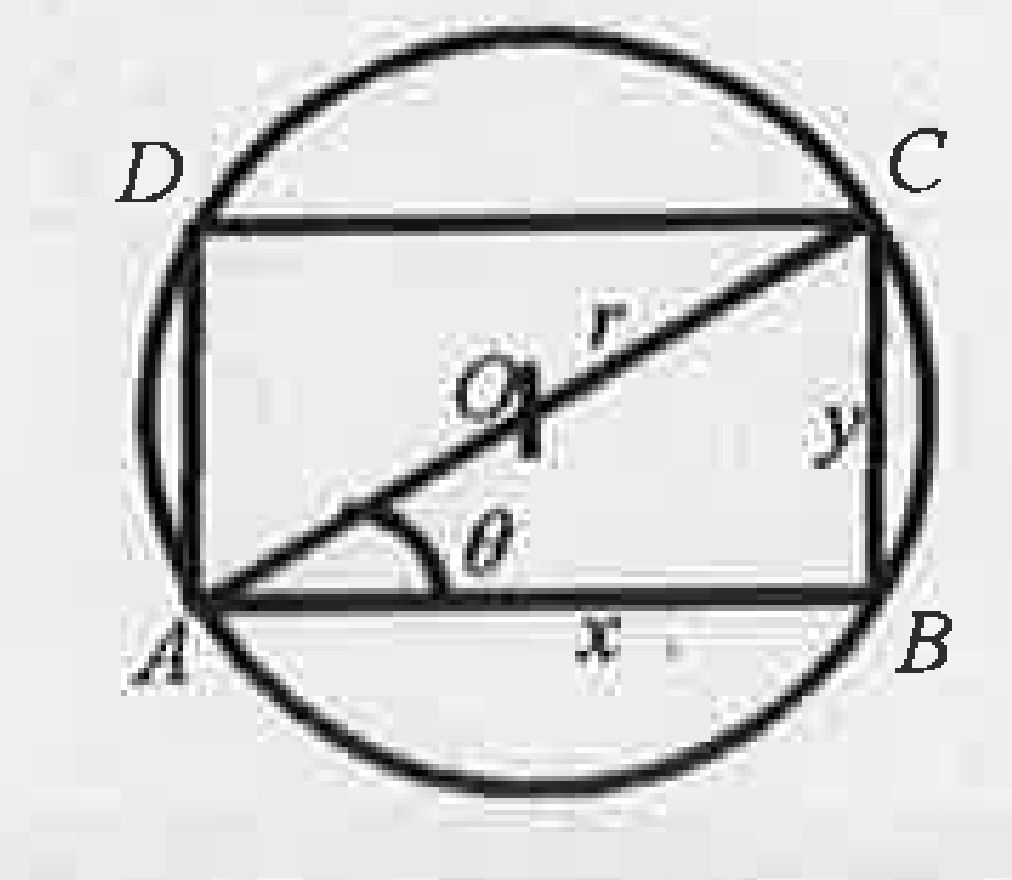
View SolutionLet x and y be the length and breadth of the rectangle ABCD in a circle having radius r. Let `angleCAB=theta` (Ref. Figure). If `triangle` represent area of the rectangle and r is a constant.
Find `(d triangle)/(d theta)` and `(d^2 triangle)/(d theta^2)`.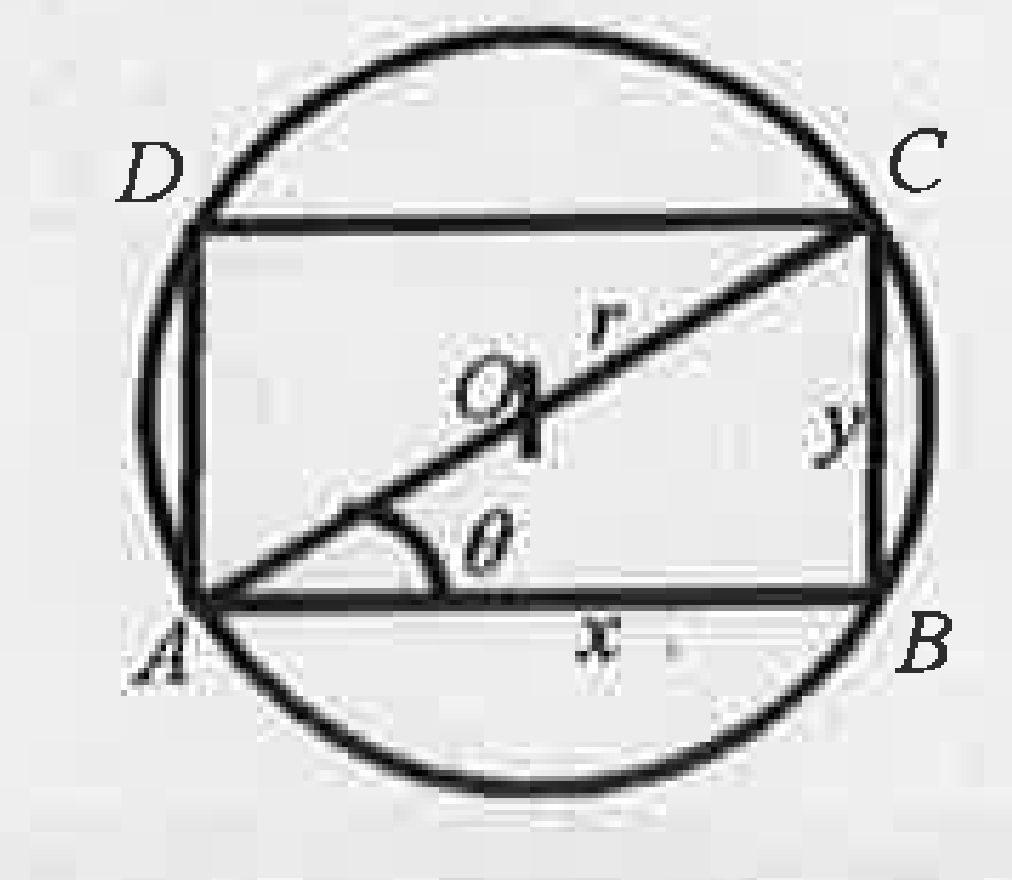
View SolutionLet x and y be the length and bredth of the rectangle ABCD in a circle having radius r. Let `angleCAB=theta` (Ref. Figure). If `triangle` represent area of the rectangle and r is a constant.
Hence find the maximum value of `triangle`.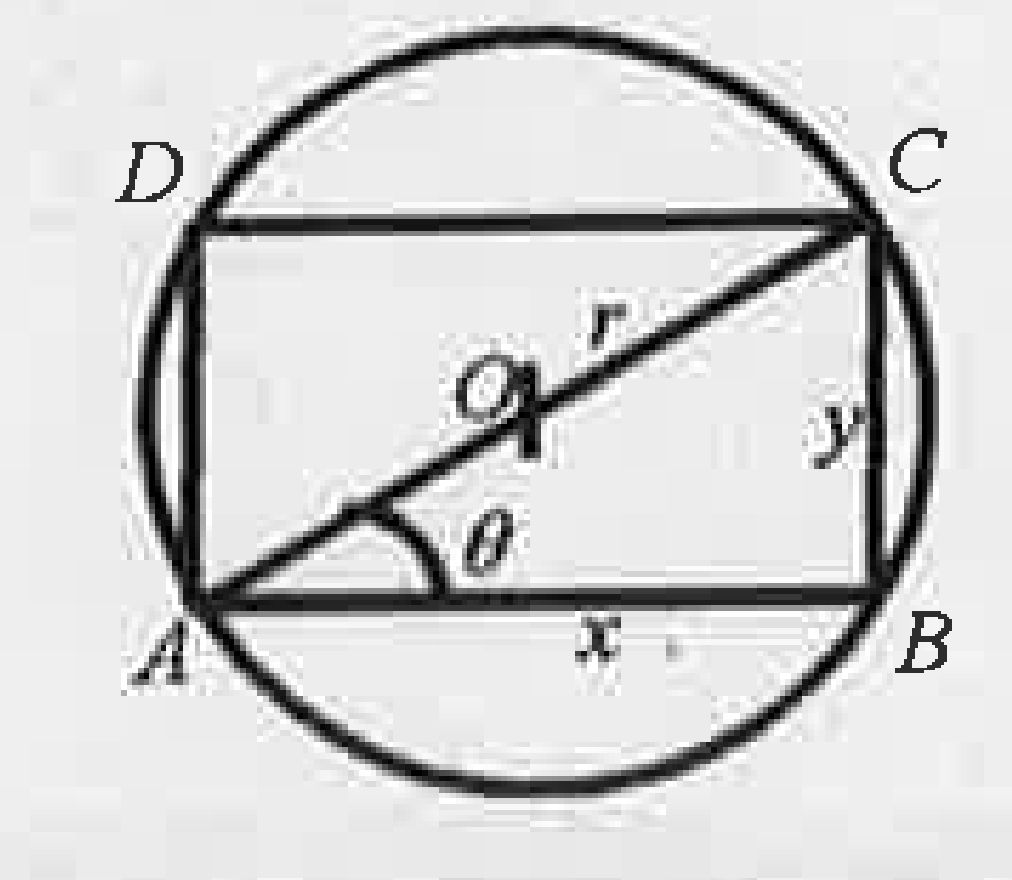
View SolutionLet x and y be the length and bredth of the rectangle ABCD in a circle having radius r. Let `angleCAB=theta` (Ref. Figure). If `triangle` represent area of the rectangle and r is a constant.
Show that the rectangle of maximum area that can be inscribed in a circle of radius r is a square of side `sqrt2r`.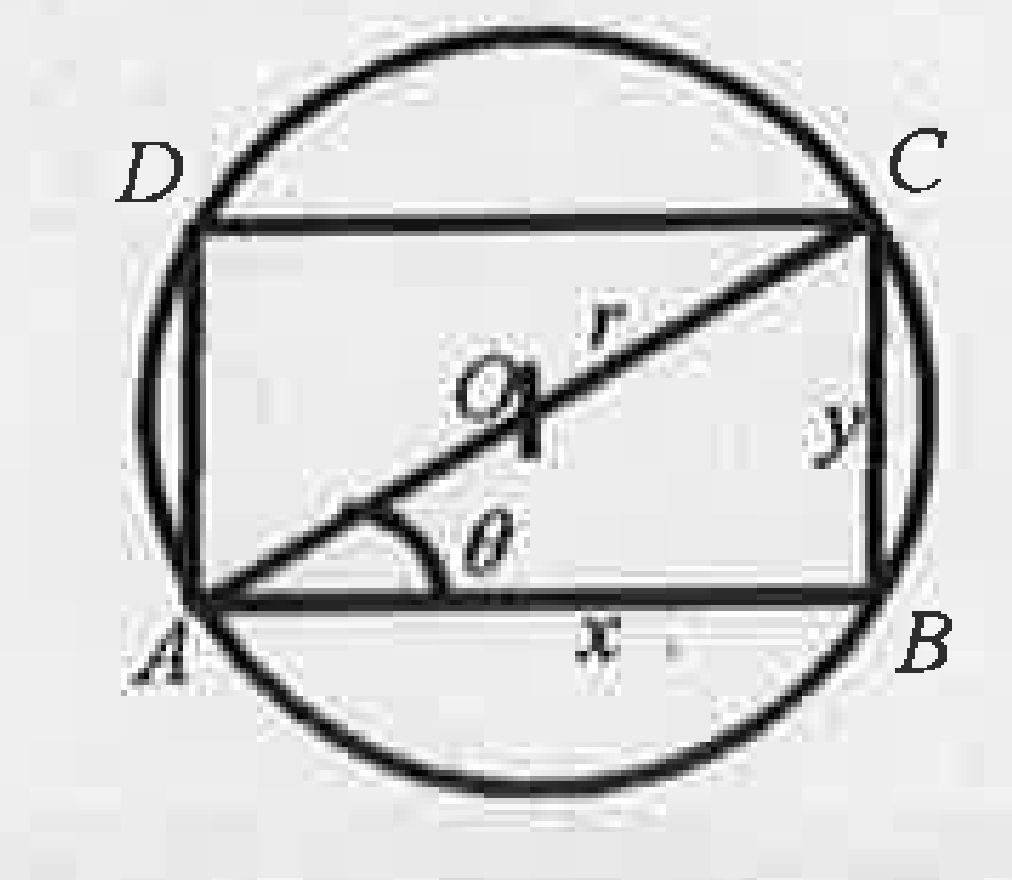
View SolutionThe second derivative of the equation of a curve is given by the equation `x(d^2y)/(dx^2)=1`, given by y=1, `dy/dx=0` when x=1. Find the slope at x=e.
View SolutionThe second derivative of the equation of a curve is given by the equation `x(d^2y)/(dx^2)=1`, given by y=1, `dy/dx=0` when x=1.
Find the equation of the curve.
View SolutionThe second derivative of the equation of a curve is given by the equation `x(d^2y)/(dx^2)=1`, given by y=1, `dy/dx=0` when x=1.Find the equation of the normal at x=e.
View SolutionThe Given figure represents a cylinder inscribed in a sphere.
Figure
Find an expression for the volume V of the cylinder .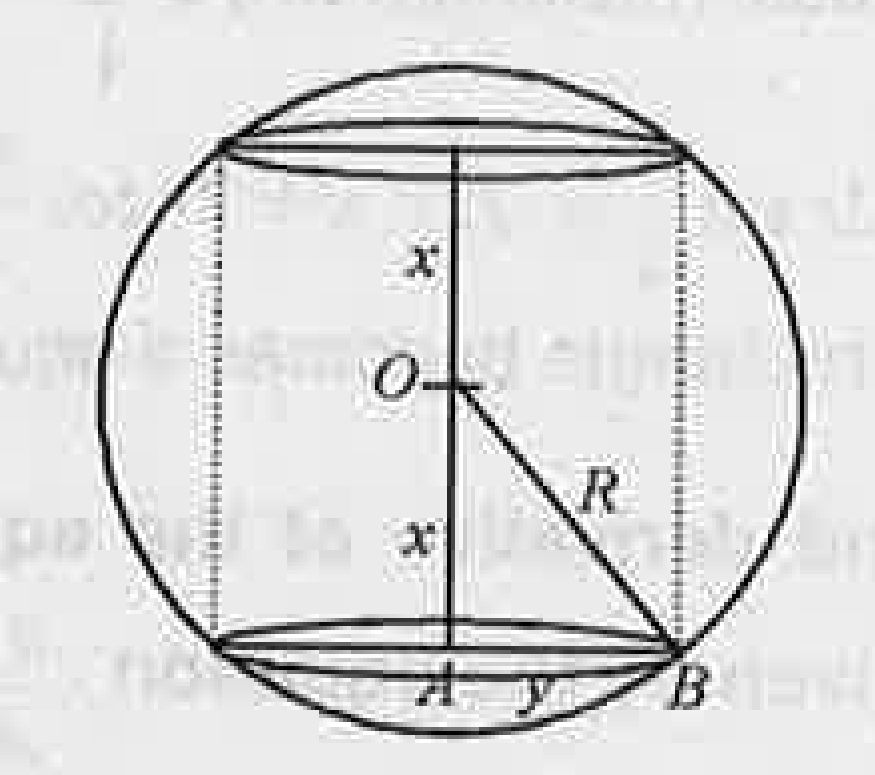
View SolutionThe Given figure represents a cylinder inscribed in a sphere.
Figure
Find the height of the cylinder when its volume V is maximum.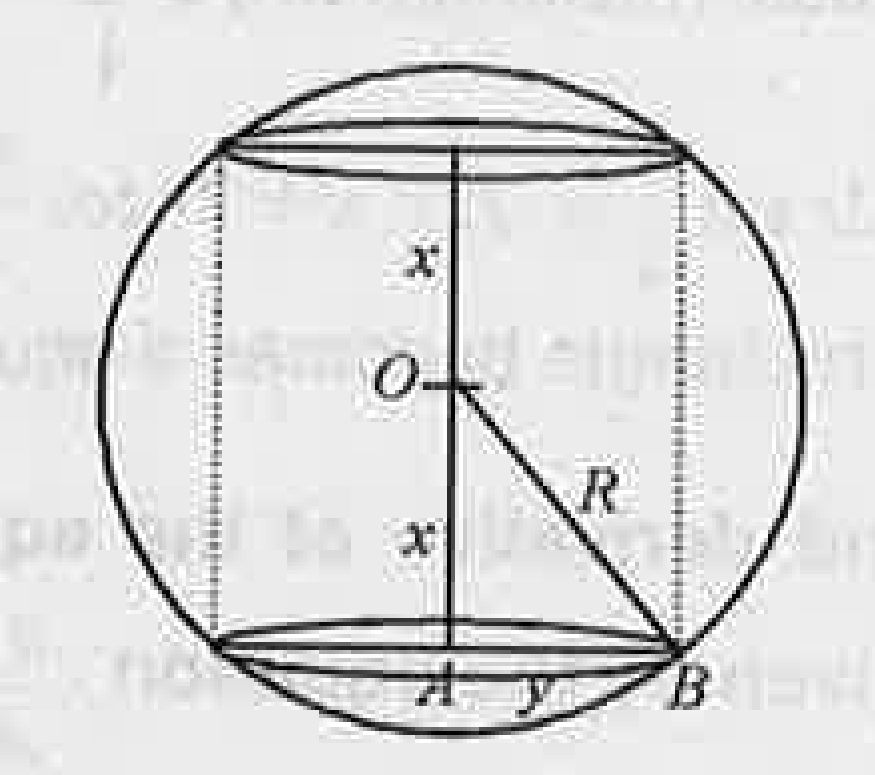
View SolutionThe Given figure represents a cylinder inscribed in a sphere.
Find the volume and radius of the largest cylinder.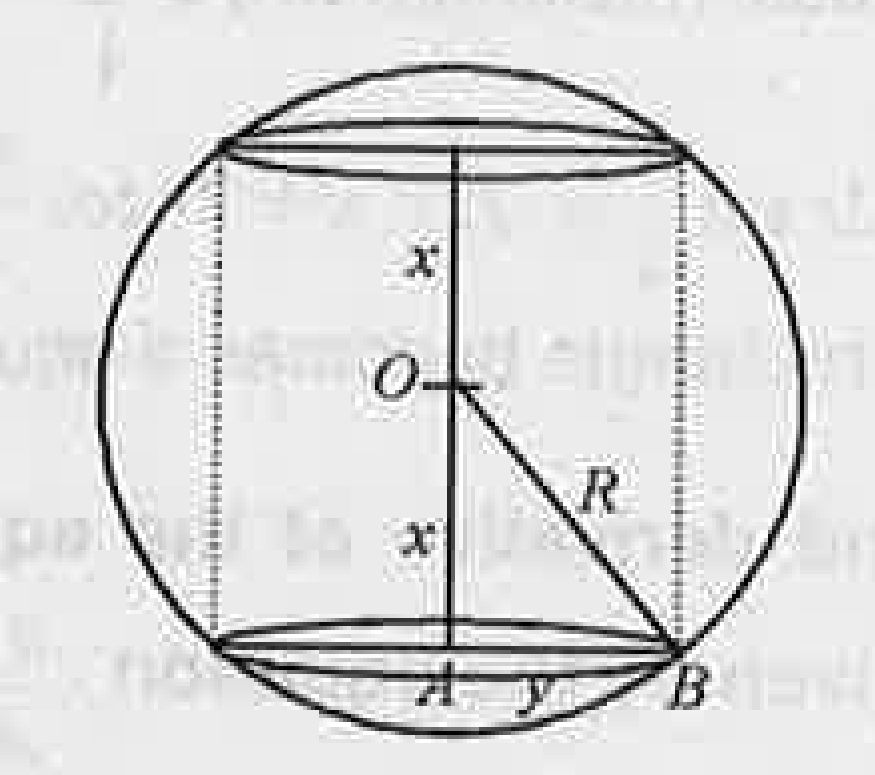
View SolutionIf `f(x)=x^3+3x^2-9x+4` is a real function
Find the intervals in which the fuction is increasing or decreasing.
View SolutionIf `f(x)=x^3+3x^2-9x+4` is a real function
Find the point of local maxima or local minima of `f(x)`.
View SolutionIf `f(x)=x^3+3x^2-9x+4` is a real function
Find the intervals in which the fuction is increasing or decreasing.
View SolutionOf all the cylinders with given surface area, show that the volume is maximum when height is equal to the diameter of the base .
View SolutionSand is pouring from a pipe. The falling sand forms a Cone on the ground in such a way that the height of the Cone is always one-sixth of the radius of the base.
Establish a relation between the volume 'v' and height 'h' of the Cone using the given condition.
View SolutionSand is pouring from a pipe. The falling sand forms a Cone on the ground in such a way that the height of the Cone is always one-sixth of the radius of the base.
if the sand is pouring at the rate of `12 cm^3`/s ,Find the rate of change of height of the Cone.
View SolutionSand is pouring from a pipe. The falling sand forms a Cone on the ground in such a way that the height of the Cone is always one-sixth of the radius of the base.
Find `dh/dt` when h=12 cm.
View SolutionChoose the correct answer from the bracket. The rate of change of the area of a circle with respect to its radius r at r =10 cm is
View SolutionFind the intervals in which the function `f` given by `f(x)=x^2-6x+5` is
Strictly increasing.
View SolutionFind the intervals in which the function `f` given by `f(x)=x^2-6x+5` is
Strictly decreasing.
View SolutionFind the local minimum and local maximum value, if any, of the function
`f(x)=x^3-6x^2+9x+8`.
View SolutionA wire of length 28 m is cut into two pieces. One of the Pieces is be made into a square and the other in to a circle. What should be the length of the two pieces so that combined area of the square and the circle is minimum using differentiation?
View SolutionAn open box of maximum value is to be made from a square piece of tin sheet 24 cm on a side by cutting equal squares from the corners and turning of the sides.
Complete the following table.
View SolutionAn open box of maximum volume is to be made from a square piece of tin sheet 24 cm on a side by cutting equal squares from the corners and turning of the sides.
Using the table, express V as a function of x and determine its domain.
View Solution
EXAMPLE questions and complete solutions for chapter APPLICATION OF DERIVATIVES of MAXIMUM PUBLICATION of Class 12