Complete Solutions to PROBLEMS of chapter RIGID BODY DYNAMICS-II of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | RIGID BODY DYNAMICS-II |
| RESNICK AND HALLIDAY | PROBLEMS |
| Number Of Questions | 41 |
| Academic Year | 2023-24 |
A car travels at `80 km//h` on a level road in the positive direction of an x axis. Each tyre has a diameter of 66 cm. Relative to a woman riding in the car and in unit-vec notation, what are the velocity `vecv` at the (a) center, (b) top, and (c) bottom of the tyre and the magnitude a of the acceleration at the (d) center, (e) top, and (f) bottom of each tyre? Relative to a hitchhiker sitting next to the road and in unit-vec notation, what are the velocity v at the (g) center, (h) top, and (i) bottom of the tyre and the magnitude a of the acceleration at the (j) center, (k) top, and (I) bottom of each tyre?
View SolutionAn automobile traveling at `80.0 km//h` has tyres of 70.0 cm diameter. (a) What is the angular speed of the tires about their axles? (b) If the car is brought to a stop uniformly in 30.0 complete turns of the tyres (without skidding), what is the magnitude of the angular accelera tion of the wheels? (c) How far does the car move during the braking?
View SolutionA solid ball of radius 6.0 cm is initially rolling smoothly at `10 m//s` along a horizontal floor. It then rolls smoothly up a ramp until it momentarily stops. What maximum height above the floor does it reach?
View SolutionA uniform solid sphere rolls down an incline. (a) What must be the incline angle if the linear acceleration of the center of the sphere is to have a magnitude of 0.15 g? (b) If a frictionless block were to slide down the incline at that angle, would its acceleration magnitude be more than, less than or equal to 0.15 g? Why?
View SolutionFrom an initial height h, a solid ball rolls smoothly down one side of a U-shaped ramp and then moves up the other side, which is frictionless. What maximum height does the ball reach?
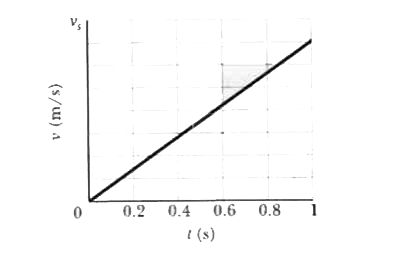
View SolutionFigure gives the speed v versus time t for a 0.500 kg object of radius 5.75 cm that rolls smoothly down a `30^(@)` ramp. The scale on the velocity axis is set by `v_(s) = 4.0 m//s`. What is the rotational inertia of the object?
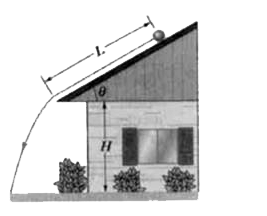
View SolutionIn Fig. a solid cylinder of radius 10 cm and mass 12 kg starts from rest and rolls without slipping a distance L = 6.0 m down a roof that is inclined at angle `theta = 30^(@)`. (a) What is the angular speed of the cylinder about its center as it leaves the roof? (b) The roof's edge is at height H = 5.0 m. How far hori zontally from the roof's edge does the cylinder hit the level ground?
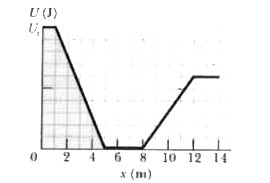
View SolutionFigure shows the potential energy U(x) of a solid ball that can roll along an x axis. The scale on the U axis is set by `U_(s) = 100 J`. The ball is uniform, rolls smoothly, and has a mass of 0.400 kg. It is released at x = 7.0 m headed in the negative direction of the x axis with a mechanical energy of 75 J. (a) If the ball can reach x = 0 m, what is its speed there, and if it cannot, what is its turning point? Suppose, instead, it is headed in the positive direction of the x axis when it is released at x = 70 m with 75 J. (b) If the ball can reach x = 13 m, what is its speed there, and if it cannot, what is its turning point?
View SolutionA hollow sphere of radius 0.15 m, with rotational inertia `I=0.048 kg.m^(2)` about a line through its center of mass, rolls without slipping up a surface inclined at `30^(@)` to the horizontal. At a certain initial position, the sphere's total kinetic energy is 20 J. (a) How much of this initial kinetic energy is rotational? (b) What is the speed of the center of mass of the sphere at the initial position? When the sphere has moved 1.0 m up the incline from its initial position, what are (c) its total kinetic energy and (d) the speed of its center of mass?
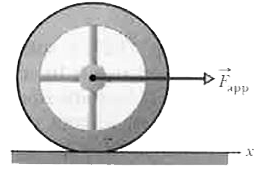
View SolutionIn Fig. a constant horizontal Force `vecF_("app")` of magnitude 10 N is applied to a wheel of mass 10 kg and radius 0.30 m. The wheel rolls smoothly on the horizontal surface, and the acceleration of its center `0.60 m//s^(2)`. (a) In unit-vec notation, what is the frictional force on the wheel? (b) What is the rotational inertia of the wheel about the rotation axis through its center of mass?
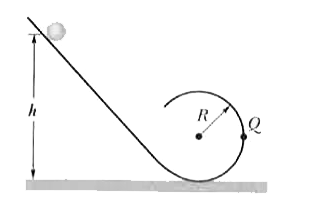
View SolutionIn Fig. a solid brass ball of mass 0.320 g will roll smoothly along a loop-the-loop track when released from rest along the straight section. The circular loop has radius R = 12.0 cm, and the ball has radius `r lt lt R`. (a) What is h if the ball is on the verge of leaving the lack when it reaches the top of the loop? If the ball is released at height h = 6.00R, what are the (b) magnitude and (c) direction of the horizontal force component acting on the ball at point Q?
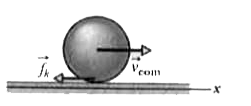
View SolutionA bowler throws a bowl ing ball of radius R= 11 cm along a lane. The ball (Fig. ) slides on the lane with initial speed `v_("com,0")= 8.5 m//s` and initial Th angular speed `omega_(0)= 0`. The coefficient of kinetic friction between the ball and the lane is 0.21. The kinetic frictional force `vecf_(k)`, acting on the ball causes a linear acceleration of the ball while producing a torque that causes an angular acceleration of the ball. When speed `v_("com")` has decreased enough and angular speed `omega` has increased enough, the ball stops sliding and then rolls smoothly. (a) What then is `v_("com")` in terms of `omega`? During the sliding, what are the ball's (b) linear acceleration and (c) angular acceleration? (d) How long does the ball slide? (e) How far does the ball slide? (f) What is the linear speed of the ball when smooth rolling begins?
View SolutionA yo-yo has a rotational inertia of `950 g cm^(2)` and a mass of 120 g. Its axle radius is 3.2 mm, and its string is 120 cm long. The yo-yo rolls from rest down to the end of the string. (a) What is the magnitude of its linear acceleration? (b) How long does it take to reach the end of the string? As it reaches the end of the string, what are its (c) linear speed, (d) translational kinetic energy, (e) rotational kinetic energy, and (f) angular speed?
View SolutionIn 1980, over San Francisco Bay, a large yo-yo was released from a crane. The 116 kg yo-yo consisted of two uniform disks of radius 32 cm connected by an axle of radius 3.2 cm. What was the magnitude of the acceleration of the yo-yo during (a) its fall and (b) its rise? (c) What was the tension in the cord on which it rolled? (d) Was that tension near the cord's limit of 52 kN? Suppose you build a scaled-up version of the yo-yo (same shape and mate rials but larger). (e) Will the magnitude of your yo-yo's acceleration as it falls be greater than, less than, or the same as that of the San Francisco yo-yo? (f) How about the tension in the cord?
View SolutionA thief intends to enter an apartment by climbing a ladder but foolishly places the upper end against a window. When he is 3.00 m up the ladder, the window is on the verge of shattering. His mass is 90.0 kg, the ladder's mass is 20.0 kg, the ladder's length is 5.00 m, and the foot of the ladder is 2.50 m from the base of the wall, on a non-slip ground surface. What are (a) the magnitude of the force on the glass from the ladder, (b) the magnitude of the force on the ladder from the ground, and (c) the angle between that ground force and the horizontal?
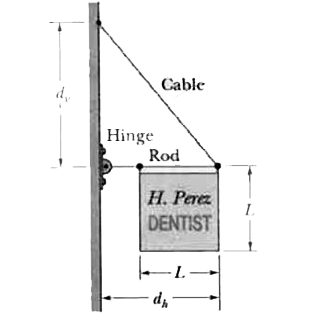
View SolutionIn Fig. a 50.0 kg uniform square sign, of edge length L= 2.50 m, is hung from a horizontal rod of length `d_(h) = 3.00 m` and negligible mass. A cable is attached to the wall. (a) What is the tension in the cable? What the end of the rod and to a point on the wall at distance `d_(h) = 4.00 m` above the point where the rod is hinged to the wall (a) what is the tension in the cable? What are the (b) magnitude and (c) direction (left or right) of the horizontal component of the force on the rod from the wall, and the (d) magnitude and (e) direction (up or down) of the vertical component of this force?
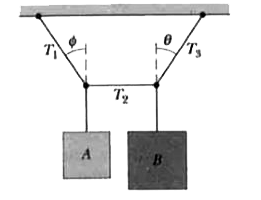
View SolutionThe system in Fig. is in equilibrium, with the string in the center exactly horizontal. Block A weighs 35 N, block B weighs 45 N, and angle `phi` is `35^(@)`. Find (a) tension `T_(1)`, (b) tension `T_(2)`, (c) tension `T_(3)`, and (d) angle `theta`.
View SolutionIn Fig. suppose the length L of the uniform bar is 2.75 m and its weight is 185 N. Also, let the block's weight W = 300 N and the angle `theta=30.0^(@)`. The wire can withstand a maximum tension of 500 N. (a) What is the maximum possible distance x before the wire breaks? With the block placed at this maximum x, what are the (b) horizontal and (c) vertical components of the force on the bar from the hinge at A?
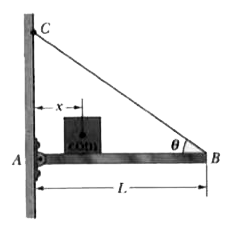
View SolutionFigure shows a horizontal uniform beam of mass `m_(b)`, and length L that is supported on the left by a hinge attached to a wall and on the right by a cable at angle `theta` with the horizontal. A package of mass `m_(p)` is positioned on the beam at a distance x from the left end. The total mass is `m_(b) + m_(p) = 79.30 kg`. Figure gives the tension T in the cable as a function of the package's position given as a fraction `x//L` of the beam length. The scale of the T axis is set by `T_(a) = 500 N` and `T_(b) = 700 N`. Evaluate (a) angle `theta`, (b) mass `m_(b)` and (c) mass `m_(p)`
View SolutionIn Fig. a 25 kg block is held in place via a pulley system. The person's upper arm is vertical, the forearm is at angle `theta = 30^(@)` with the horizontal. Forearm and hand together have a mass of 2.0 kg, with a center of mass at distance `d_(1) = 15 cm` from the contact point of the forearm bone and the upper-arm bone (humerus). The triceps muscle pulls vertically upward on the fore arm at distance `d_(2) = 2.5 cm` behind that contact point. Distance `d_(3)` is 35 cm. What are the (a) magnitude and (b) direction (up or down) of the force on the forearm from the triceps muscle and the (c) magnitude and (d) direction (up or down) of the force on the forearm from the humerus?
View SolutionA crate, in the form of a cube with edge lengths of 1.2 m, contains a piece of machinery, the center of mass of the crate and its contents is located 0.30 m above the crate's geometrical center. The crate rests on a ramp that makes an angle `theta` with the horizontal. As `theta` is increased from zero, an angle will be reached at which the crate will either tip over or start to slide down the ramp. If the coefficient of static friction between ramp and crate is 0.30, (a) does the crate tip or slide and (b) at what angle `theta` does this occur? If `mu_(s) = 0.70`, (c) does the crate tip or slide and (d) at what angle `theta` does this occur? (Hint: At the onset of tipping, where is the normal force located?)
View SolutionFigure shows a diver of weight 580 N stand ing at the end of a diving board with a length of L = 5.70 m and negligible mass. The board is fixed to two pedestals (supports) that are separated by distance d = 1.50 m. Of the forces are the (a) magnitude and (b) direction (up or down) of the force from the left ped estal and the (c) magnitude and (d) direction (up or down) of the force from the right pedestal? (e) Which pedestal (left or right) is being stretched, and (f) which pedestal is being compressed?

View SolutionA scaffold of mass 65 kg and length 5.2 m is supported in a horizontal position by a vertical cable at each end. A window washer of mass 80 kg stands at a point 1.5 m from one end. What is the tension in (a) the nearer cable and (b) the farther cable?
View SolutionIn Fig. trying to get his car out of mud, a man ties one end of a rope around the front bumper and the other end tightly around a utility pole 15 m away. He then pushes sideways on the rope at its midpoint with a force of 520 N, displacing the center of the rope 0.30 m, but the car barely moves. What is the magnitude of the force on the car from the rope? (The rope stretches somewhat.)

View SolutionA 14.0 m cord of negligible mass is stretched horizontally between two supports. When a rock climber of weight 900 N hangs from the cord's midpoint, that midpoint sags by 0.85 m. What then is the tension in the cord?
View SolutionIn Fig. the driver of a car on a horizontal road makes an emergency stop by applying the brakes so that all four wheels lock and skid along the road. The coefficient of kinetic friction between tires and road is 0.37. The separation between the front and rear axles is L = 4.0 m, and the center of mass of the car is located at distance d = 1.9 m behind the front axle and distance h=0.75 m above the road. The car weighs 11 kN. Find the magnitude of (a) the braking acceleration of the car, (b) the normal force on each rear wheel, (c) the normal force on each front wheel, (d) the braking force on each rear wheel, and (e) the braking force on each front wheel. (Hint: Although the car is not in translational equilibrium, it is in rotational equilibrium.)
View SolutionDraw the string of a simple archery bow back at its mid point until the string tension is twice the magnitude of your force on the string. What is the angle between the two halves of the string?
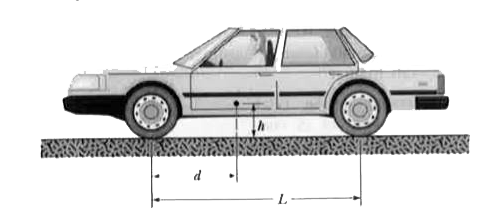
View SolutionFigure shows a vertical uniform beam of length L that is hinged at its lower end. A horizontal force `vecF_(a)` is applied to the beam at distance y from the lower end. The beam remains vertical because of a cable attached at the upper end, at angle `theta` with the horizontal. Figure gives the tension T in the cable as a function of the position of the applied force given as a fraction `y//L` of the beam length. The scale of the T axis is set by `T_(s)= 800 N`. Figure gives the magnitude `F_(h)`, of the horizontal force on the beam from the hinge, also as a function of `y//L`. Evaluate (a) angle `theta` and (b) the magnitude of `vecF_(a)`
View SolutionIn Fig. one end of a uniform beam of mass 40.0 kg is hinged to a wall: the other end is supported by a wire that makes angles `theta = 30.0^(@)` with both wall and beam. Find (a) the tension in the wire and the (b) magnitude and (c) angle from the horizontal of the force of the hinge on the beam.
View SolutionA cubical box is filled with sand and weighs 520 N. We wish to "roll" the box by pushing horizontally on one of the upper edges. (a) What minimum force is required? (b) What minimum coefficient of static friction between box and floor is required? (c) If there is a more efficient way to roll the box, find the smallest possible force that would have to be applied directly to the box to roll it. (Hint: At the onset of tipping, where is the normal force located?)
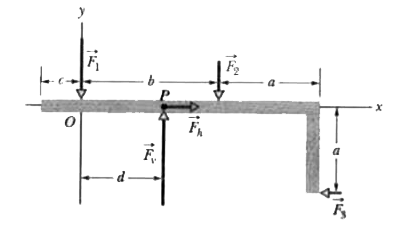
View SolutionForces `vecF_(1), vecF_(2)` and `vecF_(3)` act on the structure of Fig. shown in an overhead view. We wish to put the structure in equilibrium by applying a fourth force, at a point such as P. The fourth force has vec components `vecF_(h)` and `vecF_(v)` . We are given that `a = 2.0 m, b = 3.0 m, c = 1.0 m, F_(1) = 30 N, F_(2) = 10 N`, and `F_(3) = 5.0 N`. Find (a) `F_(h)` (b) `F_(v)` and (c) d.
View SolutionIn Fig. a 55 kg rock climber is in a lie-back climb along a fissure, with hands pulling on one side of the fissure and feet pressed against the opposite side. The fissure has width = 0.20 m, and the center of mass of the climber is a horizontal distance d = 0.40 m from the fissure. The coefficient of static friction between hands and rock is `mu_(1) = 0.45`, and between boots and rock it is `mu_(2) = 1.2`. (a) What is the least horizontal pull by the hands and push by the feet that will keep the climber stable? (b) For the horizon tal pull of (a), what must be the vertical distance h between hands and feet? If the climber encounters wet rock, so that `mu_(1)` and `mu_(2)` are reduced, what happens to (c) the answer to (a) and (d) the answer to (b)?

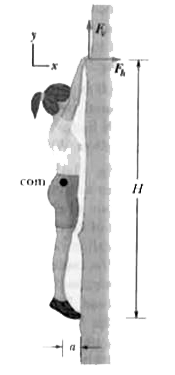
View SolutionFigure shows a 75 kg climber hanging by only the crimp hold of one hand on the edge of a shallow hori zontal ledge in a rock wall. (The fingers are pressed down to gain purchase.) Her feet touch the rock wall at distance H = 2.0 m directly below her crimped fingers but do not provide any support. Her center of mass is distance a = 0.18 m from the wall. Assume that the force from the ledge supporting her fingers is equally shared by the four fingers. What are the values of the (a) hori zontal component `F_(h)` and (b) vertical component `F_(v)` of the force on each fingertip?
View SolutionA uniform cubical crate is 0.850 m on each side and weighs 500 N. It rests on a floor with one edge against a very small, fixed obstruction. At what least height above the floor must a horizontal force of magnitude 400 N be applied to the crate to tip it?
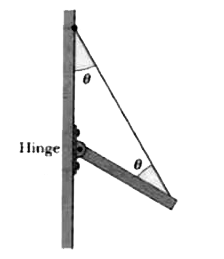
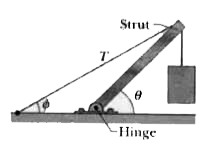
View SolutionThe system in Fig. is in equilibrium. A concrete block of mass 300 kg hangs from the end of the uniform strut of mass 45.0 kg. A cable runs from the ground, over the top of the strut, and down to the block, holding the block in place. For angles `phi = 30.0^(@)` and `theta= 45.0^(@)`, find (a) the ten sion T in the cable and the (b) magnitude and (c) angle (relative to the horizontal) of the force on the strut from the hinge.
View SolutionA uniform wood panel of mass 35.0 kg is hinged ver tically on a wall by two hinges, one 0.300 m from its top and the other 0.300 m from its bottom. The panel is 2.10 m tall and 0.910 m wide. A y axis extends upward through the hinges and an x axis extends outward along the panel's width. If each hinge supports half the panel's weight, what are the forces on the panel at (a) the top hinge and (b) the bottom hinge, both in unit-vec notation?
View SolutionIn Fig. uniform beams A and B are attached to a wall with hinges and loosely bolted together (there is no torque of one on the other). Beam A has length L = 2.40 m and mass 58.0 kg, beam B has mass 70.0 kg. The two hinge points are separated by distance d = 1.80 m. In unit-vec notation, what is the force on (a) beam A due to its hinge, (b) beam A due to the bolt, (c) beam B due to its hinge, and (d) beam B due to the bolt?
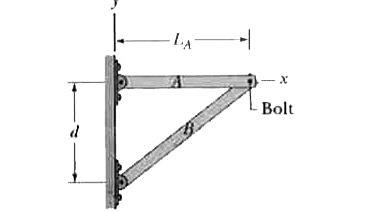
View SolutionFor the stepladder shown in Fig. sides AC and CE are each 2.44 m long and hinged at C. Bar BD is a tie rod 0.762 m long, halfway up. A man weighing 1045 N climbs 1.80 m along the ladder. Assuming that the floor is frictionless and neglecting the mass of the ladder, find (a) the tension in the tie-rod and the magnitudes of the forces on the ladder from the floor at (b) A and (c) E. (Hint: Isolate parts of the ladder in applying the equilibrium conditions.)
View SolutionA tunnel of length L = 200 m, height H = 72 m, and width 6.3 m (with a flat roof) is to be constructed at distance d = 70 m beneath the ground (Fig). The tunnel roof is to be supported entirely by square steel columns, each with a cross-sectional area of `960 cm^(2)`?. The mass of `1.0 cm^(3)` of the ground material is 2.8 g. (a) What is the total weight of the ground material the columns must support? (b) How many columns are needed to keep the compressive stress on each column at one-half its ultimate strength?

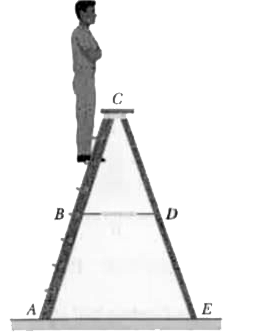
View SolutionA physics Brady Bunch, whose weights in newtons are indicated in Fig. is balanced on a seesaw. What is the number of the person who causes the smallest torque about the rotation axis at fulcrum f directed (a) out of the page and (b) into the page?
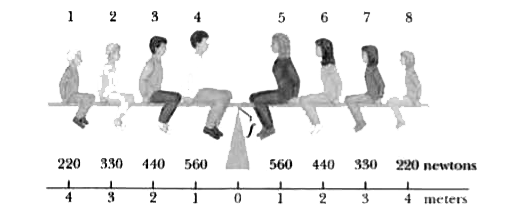
View SolutionA bowler holds a bowling ball (M = 76 kg) in the palm of his hand (Fig). His upper arm is vertical, his lower arm (1.9 kg) is horizontal. What is the magnitude of (a) the force of the biceps muscle on the lower arm and (b) the force between the bony structures at the elbow contact point?
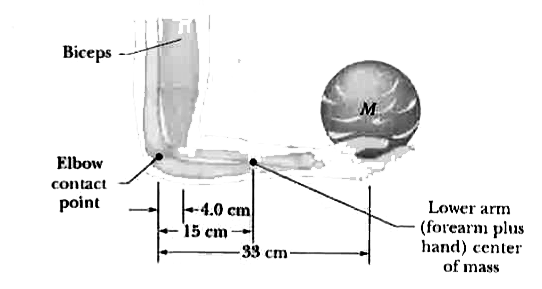
View Solution
PROBLEMS questions and complete solutions for chapter RIGID BODY DYNAMICS-II of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12