Complete Solutions to Sample Problem of chapter OSCILLATIONS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | OSCILLATIONS |
| RESNICK AND HALLIDAY | Sample Problem |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
A block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0.
What are the angular frequency, the frequency, and the period of the resulting motion?
View SolutionA block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0.
What is the amplitude of the oscillation?
View SolutionA block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0.
What is the maximum speed `v_(m)` of the oscillating block, and where is the block when it has this speed?
View SolutionA block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0.
What is the magnitude `a_(m)` of the maximum acceleration of the block?
View SolutionA block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0.
What is the phase constant `phi` for the motion?
View SolutionA block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0.
What is the displacement function x(t) for the spring block system?
View SolutionAt t=0, the displacement x(0) of the block in a linear oscillator like that of Fig . 15.5 is `-8.50cm`. (Read x(0) as ''x at time zero'') The block's velocity v(0) then is `-0.920m//s`, and its acceleration a(0) is `+47.0 m//s^(2)`.
What is the angular frequency `omega` of this system?
View SolutionAt t=0, the displacement x(0) of the block in a linear oscillator like that of Fig . 15.5 is `-8.50cm`. (Read x(0) as ''x at time zero'') The block's velocity v(0) then is `-0.920m//s`, and its acceleration a(0) is `+47.0 m//s^(2)`.
What are the phase constant `phi` and amplitude `x_(m)`?
View SolutionIf the position of the block in a block-spring oscillator is given by
`x(t) = (3.00 xx 10^(-3)m) cos [(4.00 "rad/s") t + 0.120"rad"]`, what is the block's position, velocity and acceleration at time t= 2.30s?
View SolutionAt t=0, the displacement x(0) of the block in a linear oscillator like that of Fig. 15.5 is `-8.50cm`. (Read x(0) as ''x at time zero''). The block's velocity v(0) then is `-0.920m//s`, and its acceleration a(0) is `+47.0 m//s^(2)`.
What is the angular frequency `omega` of this system?
View SolutionAt t=0, the displacement x(0) of the block in a linear oscillator like that of Fig. 15.5 is `-8.50cm`. (Read x(0) as ''x at time zero''). The block's velocity v(0) then is `-0.920m//s`, and its acceleration a(0) is `+47.0 m//s^(2)`.
What is the phase constant `phi` and amplitude `x_(m)` ?
View SolutionWrite equation of SHM of angular frequency `omega` and amplitude `x_(m)` if the particle is situated at `x_(m)//sqrt2` at t= 0 and is going toward mean position.
View SolutionA particle move along y-axis according to equation `y =3+4 cos omega t`. The motion of the particle is
View SolutionA particle is moving on y axis under a varible force `F= - ky + C`.
If in part (a) `F= - 10y + 20`, and mass m of the particle is 2.5kg and it is released from rest from `y = +3`, at t= 0, write the equation of SHM.
View SolutionMany tall building have mass dampers, which are antisway devices to prevent them from oscillating in a wind. The device might be a block oscillating at the end of a spring and on a lubricated track. If the building sways, say eastward, the block also moves eastward but delayed enough so that when it finally moves, the building is then moving back westward. Thus, the motion of the oscillator is out of step with the motion of the building. Suppose the block has mass `m= 2.72 xx 10^(5)kg` and is designed to oscillate at frequency f= 10.0 Hz and with amplitude `x_(m) = 20.0cm`.
What is the total mechanical energy E of the spring block system?
View SolutionMany tall building have mass dampers, which are antisway devices to prevent them from oscillating in a wind. The device might be a block oscillating at the end of a spring and on a lubricated track. If the building sways, say eastward, the block also moves eastward but delayed enough so that when it finally moves, the building is then moving back westward. Thus, the motion of the oscillator is out of step with the motion of the building. Suppose the block has mass `m= 2.72 xx 10^(5)kg` and is designed to oscillate at frequency f= 10.0 Hz and with amplitude `x_(m) = 20.0cm`.
What is the block's speed as it passes through the equilibrium point?
View SolutionA block of mass 4m is attached to a vertical spring of spring constant k. The block is made by gluing two blocks of mass 3m and m, respectively. Initially, the block is in equilibrium and at rest (Fig. 15.13a). At t=0, the part of the block having ass 3m falls down. Considering hanging point on ceiling as y=0 and downward direction as positive y, find y-coordinate of mass m as a function of time.
View Solution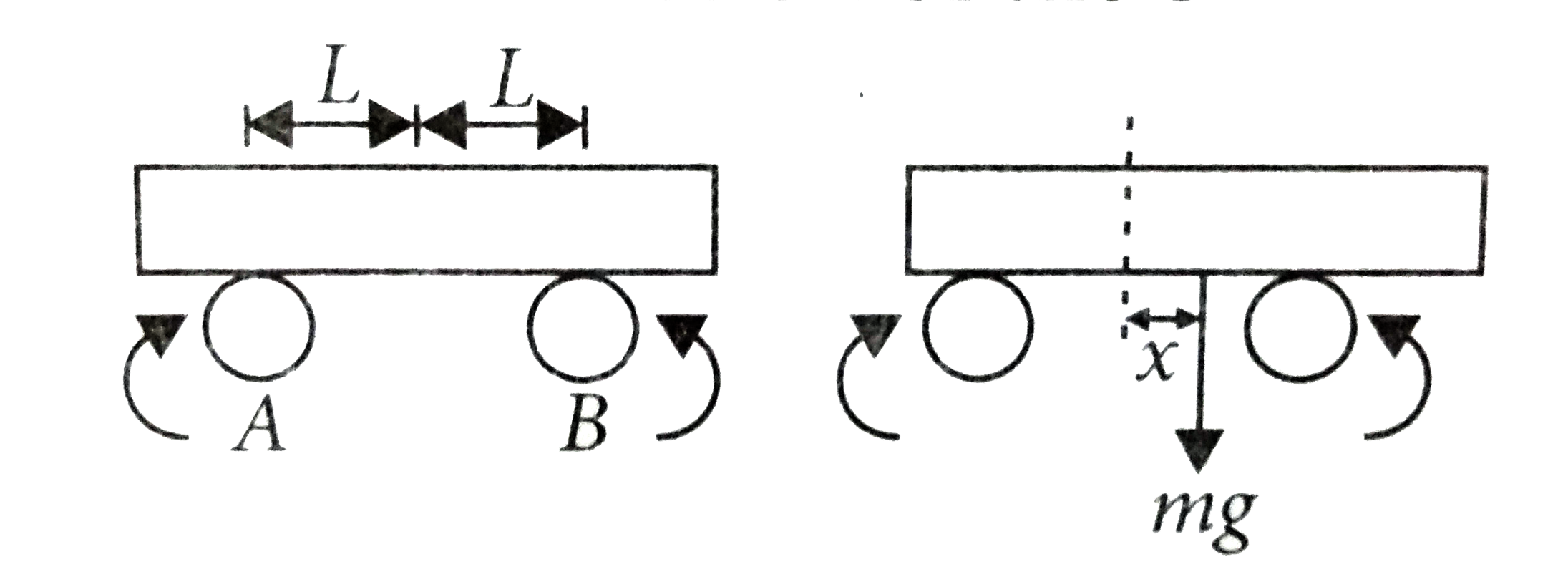
A uniform bar with mass m lies symmetrically across two rapidly rotating fixed rollers, A and B with distance L=2.0 cm between the bar's centre of mass and each roller. The rollers, whose directions of rotation are shown in figures slip against the bar with coefficient of kinetic friction `mu_(k)=0.40`. suppose the bar is displaced horizontally by the distance x as shown in figure and then released. the angular frequency `omega` of the resulting horizontal simple harmonic motion of the bar is (in `rad" "s^(-1)`)
View SolutionFigure 15.16a shows a thin rod whose length L is 12.4cm and whose mass m is 135g, suspended at its midpoint from a larg wire. Its period `T_(a)` of angular SHM is measured to be 2.53s. An irregularly shaped object, which we call object X, is then hung from the same wire, as in Fig. 15.13b, and its period `T_(b)` is found to be 4.76s. What is the rotational inertia of object X about its suspension axis?
View SolutionIn Fig 15.19a, a meter stick swings about a pivot point at one end, at distance h from the stick's center of mass.
What is the period of oscillation T?
View SolutionIn Fig 15.19a, a meter stick swings about a pivot point at one end, at distance h from the stick's center of mass.
What is the distance `L_(0)` between the pivot point O of the stick and the center of oscillation of the stick?
View SolutionFor the damped oscillator of Fig. 15.20, m= 250g, k= 85N/m, and b= 70g/s
What is the period of the motion?
View SolutionFor the damped oscillator of Fig. 15.20, m= 250g, k= 85N/m, and b= 70g/s
How long does it take for the amplitude of the damped oscillations to drop to half its initial value?
View SolutionFor the damped oscillator of Fig. 15.20, m= 250g, k= 85N/m, and b= 70g/s
How long does it take for the mechanical energy to drop to one-half its initial value?
View Solution
Sample Problem questions and complete solutions for chapter OSCILLATIONS of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12