Complete Solutions to Practice Questions of chapter OSCILLATIONS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | OSCILLATIONS |
| RESNICK AND HALLIDAY | Practice Questions |
| Number Of Questions | 57 |
| Academic Year | 2023-24 |
Which one of the following statement is true concerning an object executing simple harmonic motion?
View SolutionResonance occurs in harmonic motion when
View SolutionA simple pendulum has length L and period T. As it passes through its equilibrium position, the string is suddenly clamped at its midpoint. The period then becomes
View SolutionAn object of mass m, oscillating on the end of a spring with spring constant k has amplitude A. its maximum speed is
View SolutionThe velocity of a certain simple harmonic oscillator is given by `v= -(12 m//s) sin [(6.0 "rad"//s)t]`. What is the amplitude of the simple harmonic motion?
View SolutionA 0.20kg object mass attached to a spring whose spring constant is 500N/m executes simple harmonic motion. If its maximum speed is 5.0m/s, the amplitude of its oscillation is
View SolutionA ball hung from a vertical spring oscillates in simple harmonic motion with an angular frequency of 2.6 rad/s and an amplitude of 0.075m. What is the maximum acceleration of the ball?
View SolutionA 1.2kg mass is oscillating without friction on a spring whose spring constant is 3400N/m. When the mass's displacement is 7.2cm. What is its acceleration?
View SolutionThe displacement of an object oscillating on a spring is given by `x(t) = x_(m) cos (omega t+ phi)`. If the initial displacement is zero and the initial velocity is in the negative x direction. Then the phase constant `phi` is
View SolutionThe displacement of an object oscillating on a spring is given by `x(t) = x_(m) cos (omega t +phi)`. If the object is initially displacement in the negative x direction and given a negative initialy velocity, then the phase constant `phi` is between
View SolutionA 0.25kg block oscillates on the end of the spring with a spring constant of 200N/m. If the oscillation is started by elongating the spring 0.15m and giving the block a speed of 3.0m/s, then the maximum speed of the block is
View SolutionThe amplitude of oscillation of a simple pendulum is increased from `1^(@) " to " 4^(@)`. Its maximum acceleration changes by a factor of
View SolutionA particle undergoes damped harmonic motion. The spring constant is 100N/m, the damping constant is `8.0 xx 10^(-3)kg m//s`, and the mass is 0.50kg. If the particle starts at its maximum displacement, x= 1.5m at time t=0, what is the particle's position at t= 5.0s?
View SolutionFive particles undergo damped harmonic motion. Value for the spring constant k, the damping constantb, ad the mass m are given below. Which leads to the smallest rate of loss of mechanical energy?
View SolutionA particle is osicllating according to the equation `X= 7 cos (0.5 pi t)`, where t is in second. The point moves from the position of equilibrium to maximum displacement in time
View SolutionAn archer pulls the bowstring back for a distance of 0.470m befor releasing the arrow. The bow and string act like a spring whose spring constant is 425N/m. (a) What is the elastic potential energy of the drawn bow?
View SolutionA simple pendulum is made from a 0.65m long string and a small ball attached to its free end. The ball is pulled to one side through a small angle and then released from rest. After the ball is released, how much time elaspses before it attains its greatest speed?
View SolutionThe length of a simple pendulum is 0.79m and the mass of the particle (the ''bob'') at the end of the cable is 0.24kg. The pendulum is pulled away from its equilibrium position by an angle of `8.50^(@)` and released from rest. Assume that friction can be neglected and that the resulting oscillatory motion is simple harmonic motion. What is the angular frequency of the motion?
View SolutionA block is attached to a horizontal spring and oscillates back and forth on f frictionless horizontal surface at a frequency of 3.00Hz. The amplitude of the motion is `5.08 xx 10^(-2)m`. At the point where the block has its maximum speed, it suddenly splits into two identical parts, only one part remaining attached to the spring. What is the amplitude and the frequency of the simple harmonic motion that exists after the block splits?
View SolutionA copper rod (length =2.0m, radius `=3.0 xx 10^(-3)m`) hangs down from the ceiling. A 9.0kg object is attached to the lower end of the rod. The rod acts as a ''spring'' and the object oscillates vertically with a small amplitude. Ignoring the rod's mass, find the frequency f of the simple harmonic motion.
View SolutionTwo physical pendulums (not simple pendulums) are made from meter sticks that are suspended from the ceiling at one end. They are identical, except that one is made of wood and the other of metal. They are set into oscillation and execute simple harmonic motion. The wood and metal pendulums have masses of 0.17 and 0.85kg, respectively. Determine the period of wood pendulum.
View SolutionThe position of a simple harmonic oscillator is given by `x(t) = (0.50) cos ((pi)/(3)t)`, where t is measured in seconds. What is the maximum velocity of this oscillator?
View SolutionThe acceleration of a certain simple harmonic oscillator is given by `a = -(15.8 m//s^(2)) cos (2.51 t)`. What is the amplitude of the simple harmonic mootion?
View SolutionA 1.0kg block oscillates with a frequency of 10Hz at the end of a certain spring. The spring is then cut into two halves. The 1.0kg block is then made to oscillate at the end of one of the halves. What is the frequency of oscillation of the block?
View SolutionA simple harmonic oscillator with a period of 2.0s is subject to damping so that it loses one percent of its amplitude per cycle. About how much energy does this oscillator lose per cycle?
View SolutionA pendulum is transported from sea-level, where the acceleration due to gravity g is `9.80m//s^(2)`, to the bottom of Death Valley. At this location, the period of the pendulum is decreased by 3.00%. What is the vaue of g in Death Valley?
View SolutionIn a certain clock, a pendulum of length `L_(1)`, has a period `T_(1) = 0.95s`. The length of the pendulum is adjusted is adusted to a new `L_(2)` such that `T_(2) = 1.0s`. What is the ratio `L_(2)//L_(1)`?
View SolutionA simple pendulum consists of a ball of mass m suspended from the ceiling using a string of length L. The ball is displaced from its equilibrium position by a small angle `theta`. What is the magnitude of the restoring force that moves the toward its equilibrium position and produces simple harmonic motion?
View SolutionAn iron ball hangs from a 21.5m steel cable and is used in the demolition of a building at a location where the acceleration due to gravity is `9.75m//s^(2)`. The ball is swung outward from its equilibrium position for a distance of 4.20m. Assuming the system behaves as a simple pendulum, find the maximum speed of the ball during its swing.
View SolutionThe motion of a particle is given by `x=A sin omegat+Bcos omegat`. The motion of the particle is
View SolutionA particle executes simple harmonic motion with a frequency. (f). The frequency with which its kinetic energy oscillates is.
View SolutionA thin uniform rod of length l is pivoted at its upper end. It is free to swing in a vertical plane. Its time period for oscillation of small amplitude is
View SolutionA particle moves on the X-axis according to the equation `x=x_0 sin^2omegat`. The motion simple harmonic
View SolutionStatement 1: While crossing a bridge, soldiers are asked to break steps.
Statement 2: When natural frequency of an oscillating system equals frequency of external impulse, its amplitude of oscillating may become very high.
View SolutionTwo springs of spring constant `6 N//m` and `4 N//m` are attached to a block of mass 1 kg and to fixed support. Then time period of the given oscillation is
(consider `sqrt(10) = pi`)
View SolutionTime period of vertical oscillation of the block in the system in the figure is
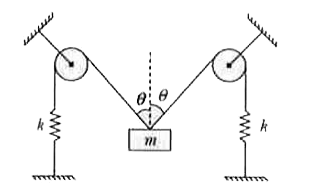
View SolutionA particle moves in the xy plane according to the equation
`vec(r )= (hat(i) + 2hat(j))A cos omega t`
The motion of the particle is
View SolutionAn object is released from rest. The time it takes to fall through a distance h and the speed of the object as it falls through this distance are measured with a pendulum clock. The entire apparatus is taken on the Moon and the experiment is repeated. Then,
View SolutionWhich of the following quantities are always negative in a simple harmonic motion?
View SolutionThe amplitude of a particle executing SHM about `O` is `10 cm`. Then
View SolutionA (hypothetical) large slingshot is stretched 2.30 m to launched a 170 g projectile with speed sufficient to escape from Earth `(11.2 km//s)`. Assume the elastic bands of the slingshot obey Hooke's law.
What is the spring constant of the device if all the elastic potential energy is converted to kinetic energy?
View SolutionA (hypothetical) large slingshot is stretched 2.30 m to launched a 170 g projectile with speed sufficient to escape from Earth `(11.2 km//s)`. Assume the elastic bands of the slingshot obey Hooke's law.
Assume that an average person can be exert a force of 490 N. How many people are required to stretch the elastic bands?
View SolutionA 2.0 - kg block executes SHM while attached to a horizontal spring of spring constant `200 N//m`. The maximum speed of the block as it slides on a horizontal frictionless surface is `3.0 m//s`.
What is the amplitude of the block's motion?
View SolutionA 2.0 - kg block executes SHM while attached to a horizontal spring of spring constant `200 N//m`. The maximum speed of the block as it slides on a horizontal frictionless surface is `3.0 m//s`.
What is the magnitude of its maximum and minimum accelerations?
View SolutionA 2.0 - kg block executes SHM while attached to a horizontal spring of spring constant `200 N//m`. The maximum speed of the block as it slides on a horizontal frictionless surface is `3.0 m//s`.
How long does the block take to complete 7.0 cycles of its motion?
View SolutionA block weighing 10.0 N is attached to the lower end of a verticle spring `(k = 200.0 N//m)`, the other end of which is attached to a ceiling. The block oscillates vertically and has a kinetic energy of 2.00 J as it passes through the point at which the spring is unstretched.
What is the period of the oscillation?
View SolutionA block weighing 10.0 N is attached to the lower end of a verticle spring `(k = 200.0 N//m)`, the other end of which is attached to a ceiling. The block oscillates vertically and has a kinetic energy of 2.00 J as it passes through the point at which the spring is unstretched.
Use the law of conservation of energy to determine the maximum distance the block moves both above and below the point at which the spring is unstretched (these are not necessarily the same)
View SolutionA block weighing 10.0 N is attached to the lower end of a verticle spring `(k = 200.0 N//m)`, the other end of which is attached to a ceiling. The block oscillates vertically and has a kinetic energy of 2.00 J as it passes through the point at which the spring is unstretched.
What is the amplitude of the oscillation and the maximum kinetic energy of the block as it oscillates?
View SolutionMatch the statement in Column I with the statements in Column II. One or more than one choice from ColumnII can match with a statement from Column I.

View SolutionIn the given table, Column I gives type of motion, Column II gives the path traced and Column III gives other characteristic of the motion.


Choose the combination that defines the characteristics of periodic motion.
View SolutionIn the given table, Column I gives type of motion, Column II gives the path traced and Column III gives other characteristic of the motion.


Choose the combination that defines the characteristics of simple harmonic motion.
View SolutionIn the given table, Column I gives type of motion, Column II gives the path traced and Column III gives other characteristic of the motion.

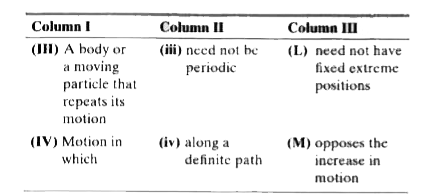
Choose the combination that defines the characteristics of simple harmonic motion.
View SolutionIn the given table, Column I gives type of oscillation, Column II gives change in amplitude of oscillation and Column III gives examples of these types of oscillation.

The combination that defines the features of damped oscillation is
View SolutionIn the given table, Column I gives type of oscillation, Column II gives change in amplitude of oscillation and Column III gives examples of these types of oscillation.

The combination that defines the features of forced oscillation is
View SolutionIn the given table, Column I gives type of oscillation, Column II gives change in amplitude of oscillation and Column III gives examples of these types of oscillation.

The combination that defines the features of free oscillation is
View SolutionWhen a 20 N can is hung from the bottom of a vertical spring, it causes the spring to stretch 20 cm. The spring is now placed horizontal on a frictionless table. One end of it is held fixed, and the other end is attached to a 5.0 N can. The can is then moved (stretching the spring) and released from rest. What is the period `("in" xx 10^(-2)s)` of the resulting oscillation?
View SolutionAn engineer has odd-shaped 10 kg object needs to find its rotational inertia about an axis through its center of mass. The object is supported on a wire stretched along the desired axis. The wire has a torsion constant `k = 0.50 N.m`. If this torsion pendulum oscillates through 20 cycles in 50 s, what is the rotational inertia `("in" 10^(-2) kg m^(2))` of the object?
View Solution
Practice Questions questions and complete solutions for chapter OSCILLATIONS of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12