Complete Solutions to Problems of chapter OSCILLATIONS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | OSCILLATIONS |
| RESNICK AND HALLIDAY | Problems |
| Number Of Questions | 39 |
| Academic Year | 2023-24 |
Hanging from a horizontal beam are nine simple pendulums of the following lengths: (a) 0.10, (b) 0.30, (c ) 0.70, (d) 0.80, (e ) 1.2 (f) 2.6 (g) 3.5 (h) 5.0 and (i) 6.2m. Suppose the beam undergoes horizontal oscillations with angular frequencies in the range from 2.00 rad/s to 4.00 rad/s. Which of the pendulums will be (strongly) set in motion?
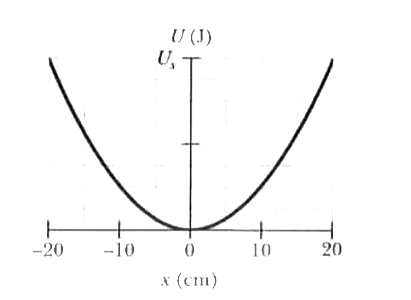
View SolutionFigure 15-24 gives the one-dimensional potential energy well for a 4.0kg particle (the function U (x) has the form `bx^(2)` and the vertical axis scale is set by U= 2.0 J). (a) If the particle passes through the equilibrium position with a velocity of 85 cm/s, will it be turned back before it reaches x= 15cm? (b) If yes, at what position, and if no, what is the speed of the particle at x= 15cm?
View SolutionAn oscillator consists of a block of mass 0.500kg connected to a spring. When set into oscillation with amplitude 35.0 cm, the oscillator repeats its motion every 0.350s. Find the (a) period, (b) frequency, (c ) angular frequency, (d) spring constant, (e ) maximum speed, and (f ) magnitude of the maximum force on the block from the spring.
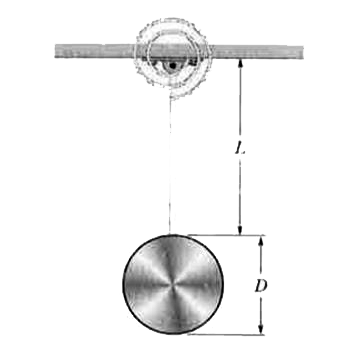
View SolutionIn Fig 15.25, a 5.00 kg dish of diameter D= 42.0 cm is supported by a rod of length L = 76.0 cm and negligible mass that is pivoted at its end. (a) With the massless torsion spring unconnected, what is the period of oscillation? (b) With the torsion spring connected, the rod is vertical at equilibrium. What is the torsion constant of the spring if the period of oscillation has been decreased by 0.500s?
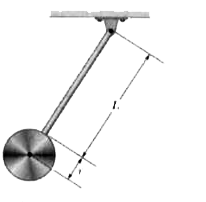
View SolutionIn Fig. 15.26, the pendulum consists of a uniform disk with radius r= 10.0cm and mass 500g attached to a uniform rod with length L = 500mm and mass 250g. (a) Calculate the rotational inertia of the pendulum about the pivot point. (b) What is the distance between the pivot point and the center of mass of the pendulum? (c ) Calculate the period of oscillation.
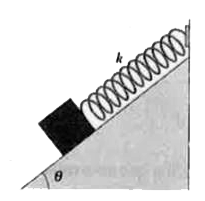
View SolutionIn Fig 15.27 a block weighing 14.0 N, which can slide without friction on an incline at angle `theta= 40.0^(@)`, is connected to the top of the incline by a massless spring of unstretched length 0.450m and spring constant 135N/m. (a) How far from the top of the incline is the block's equilibrium point ? (b) If the block is pulled slightly down the incline and released, what is the period of the resulting oscillations?
View SolutionA block of mass M = 5.4 kg at rest on a horizontal frictionless table, is attached to a rigid support by a spring of constant k= 6000N/m. A bullet of mass m= 9.5g and velocity `vec(v)` of magnitude 680 m/s strikes and is embedded in the block (Fig. 15.28). Assuming the compression of the spring is negligible until the bullet is embedded, determine (a) the speed of the block immediately after the collision and (b) the amplitude of the resulting simple harmonic motion.

View SolutionIn Fig. 15.29 two springs are joined and connected to a block of mass 0.490kg that is set oscillating over a frictionless floor. The springs each have spring constant k= 5000N/m. What is the frequency of the oscillations?
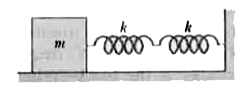
View SolutionIn an electric shaver, the blade moves back and forth over a distance of 2.0 mm in simple harmonic motion, with frequency 100Hz. Find (a) the amplitude, (b) the maximum blade speed and (c ) the magnitude of the maximum blade acceleration.
View SolutionA rectangular block, with face lengths a= 35cm and b= 45 cm, is to be suspended on a thin horizontal rod running through a narrow hole in the block. The block is then to be set swinging about the rod like a pendulum, through small angles so that is is in SHM. Figure 15.30 shows one possible position of the hole, at distance r from the block's center, along a line connecting the center with a corner. (a) Plot of the period versus distance r along that line such that the minimum in the curve is apparent. (b) For what value of r does that minimum occur? There is a line of points around the block's center for which the period of swinging has the same minimum value. (c ) What shape does that line make?
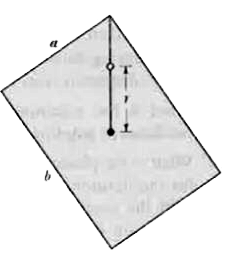
View SolutionA massless spring hangs from the ceiling with a small object attached to its lower end. The object is initially held at rest in a position y such that the spring is at its rest length. The object is then released from y and oscillates up and down, with its lowest position being 10cm below y, (a) What is the frequency of the oscillation? (b) What is the speed of the object when it is 8.0 cm below the initial position? (c ) An object of mass 600g is attached to the first object, after which the system oscillates with half the original frequency. What is the mass of the first object? (d) How far below y, is the new equilibrium (rest) position with both objects attached to the spring?
View SolutionTwo particles execute simple harmonic motion of the same amplitude and frequency along close parallel lines. They pass each other moving in opposite directions each time their displacement is half their amplitude. Their phase difference is
View SolutionFind the mechanical energy of a block-spring system with a spring constant of 1.8 N/cm and an amplitude of 2.4cm.
View SolutionAN oscillating block-spring system has a mechanical energy of 2.00J, an amplitude of 10.0cm, and a maximum speed of 0.800 m/s. Find (a) the spring constant, (b) the mass of the block and (c ) the frequency of oscillation.
View SolutionAn automobile can be considered to be mounted on four identical springs as far as vertical oscillations are concerned. The springs of a certain car are adjusted so that the oscillations have a frequency of 3.00Hz. (a) What is the spring constant of each spring if the mass of the car is 2110kg and the mass is evenly distributed over the springs? (b) What will be the oscillation frequency if five passengers, averaging 85.0kg each, ride in the car with an even distribution of mass?
View SolutionThe position function x= (6.0m) `cos [(3pi "rad"//s) t+ pi//3" rad"]` gives the simple harmonic motion of a body. At t=21s, what are the (a) displacement, (b) velocity, (c ) acceleration, and (d) phase of the motion? Also, what are the (e ) frequency and (f) period of the motion?
View SolutionTwo particles oscillate in simple harmonic motion along a common straight-line segment of length A. Each particle has a period of 1.5s but they differ in phase by `pi//6` rad. (a) How far apart are they (in terms of A) 0.60s after the lagging particle leaves one end of the path? (b) Are they then moving in the same direction, toward each other, or away from each other?
View SolutionA 10g particle undergoes SHM with an amplitude of 2.0mm, a maximum acceleration of magnitude `6.5 xx 10^(3) m//s^(2)`, and an unknown phase constant `phi`. What are (a) the period of the motion, (b) the maximum speed of the particle, and (c ) the total mechanical energy of the oscillator? What is the magnitude of the force on the particle when the particle is at (d) its maximum displacement and (e ) half its maximum displacement?
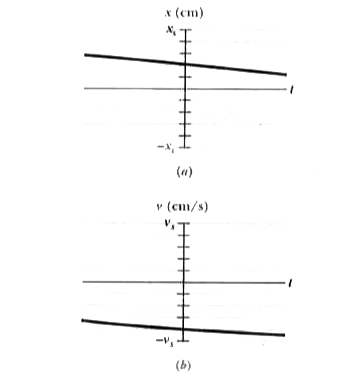
View SolutionFigure 15.32a is a partial graph of the position function x(t) for a simple harmonic oscillator with an angular frequency of 1.00 rad/s. Fig 15.32b is a partial graph of the corresponding velocity function v(t). The vertical axis scales are set by `x_(s)= 5.00cm and v_(s) = 10.0cm//s`. What is the phase constant of the SHM if the position function x(t) is in the general form `x= x_(m) cos (omega t + phi)`?
View SolutionIn Fig. 15.33, a stick of length L= 1.65 m oscillates as a physical pendulum. (a) What value of distance x between the stick's center of mass and its pivot point O gives the least period? (b) What is that least period?
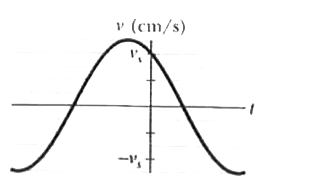
View SolutionWhat is the phase constant for the harmonic oscillator with the velocity function v(t) given in Fig. 15.34 if the position function x(t) has the form `x= x_(m) cos (omega t + phi)`? The vertical axis scale is set by `v_(x) = 8.0 cm//s`.
View SolutionWhat is the oscillation amplitude of a 4.00kg box oscillating on a spring with spring constant 100N/m if at time t= 1.00s the position is x = 0.129m and the velocity is v= 5.00m/s? At t= 0, what are (a) the position and (b) the velocity?
View SolutionA 5.00kg object on a horizontal frictionless surface is attached to a spring with k= 1000N/m. The object is displaced from equilibrium 40.0cm horizontally and given an initial velocity of 10.0m/s back toward the equilibrium position. What are (a) the motion's frequency (b) the initial potential energy of the block-spring system, (c ) the initial kinetic energy and (d) the motion amplitude?
View SolutionWhat is the maximum acceleration of a platform that oscillates at amplitude 2.50cm and frequency 6.60Hz?
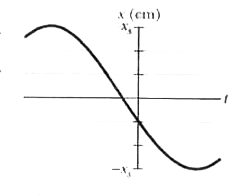
View SolutionWhat is the phase constant for the harmonic oscillator with the position function x(t) given in Fig. 15.36 if the position function has the form `x= x_(m) cos (omega t + phi)`? The vertical axis scale is set by `x_(s) = 9.0cm`
View SolutionA body undergoes simple harmonic motion of amplitude 4.25cm and period 0.200s. The magnitude of the maximum force acting on it is 10.0N. (a) What is the mass? (b) If the oscillations are produced by a spring, what is the spring constant?
View SolutionA thin uniform rod (mass= 0.90kg) swings about an axis that passes through one end of the rod and is perpendicular to the plane of the swing. The rod swings with a period of 1.5s and an angular amplitude of `10^(@)`. (a) What is the length of the rod? (b) What is the maximum kinetic energy of the rod as it swings?
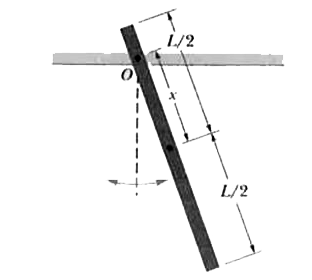
View SolutionA pendulum is formed by pivoting a long thin rod about a point on the rod. In a series of experiments, the period is measured as a function of the distance x between the pivot point and the rod's center. (a) If the rod's length is L= 2.20 m and its mass is m= 22.1g, what is the minimum period? (b) If x is chosen to minimize the period and then L is increased does the period increase, decrease, or remain the same? (c ) If, instead, m is increased without L increasing does the period increase, decrease or remain the same?
View SolutionThe 0.800kg cube in Fig. 15.38 has edge lengths d= 6.00cm and is mounted on an axle through its center. A springs (k= 3600N/m) connects the cube's upper corner to a rigid wall. Initially the spring is at its rest length. If the cube is rotated `3^(@)` and released, what is the period of the resulting SHM?

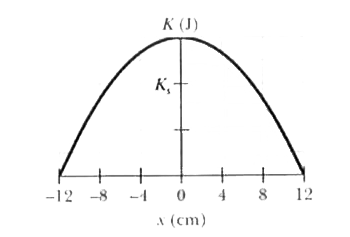
View SolutionFigure 15.39 shows the kinetic energy K of a simple harmonic oscillator versus its position x. The vertical axis scale is set by `K_(s)= 8.0J`. What is the spring constant?
View SolutionAn object undergoing simple harmonic motion takes 0.25g to travel from one point of zero velocity to the next such point. The distance between those points is 32cm. Calculate the (a) period (b) frequency and (c ) amplitude of the motion.
View SolutionIf the phase angle for a block -spring system in SHM is `pi//8` rad and the block's position is given by `x= x_(m) cos(omega t + phi)`, what is the ratio of the kinetic energy to the potential energy at time t= 0?
View SolutionAn oscillator consists of a block attached to a spring (k= 425N/m). At some time t, the position (measured from the system's equilibrium location), velocity and acceleration of the block are x= 0.100m, `v= 13.6m//s, and a= -123m//s^(2)`. Calculate (a) the frequency of oscillation, (b) the mass of the block and (c ) the amplitude of the motion.
View SolutionAn oscillating block-spring system takes 0.25s to begin repeating its motion. Find (a) the period, (b) the frequency in hertz, and (c ) the angular frequency in radians per second.
View SolutionA particle with a mass of `3.00 xx 10^(-20)kg` is oscillating with simple harmonic motion with a period of `2.00 xx 10^(-5)s` and a maximum speed of `1.00 xx 10^(3) m//s`. Calculate (a) the angular frequency and (b) the maximum displacement of the particle.
View SolutionWhen the displacement in SHM is 0.40 times the amplitude `x_(m)`, what fraction of the total energy is (a) kinetic energy and (b) potential energy? (c ) At what displacement, in terms of the amplitude, is the energy of the system half kinetic energy and half potential energy?
View SolutionA block rides on a piston (a squatcylindrical piece) that is moving vertically with simple harmonic motion. (a) If the SHM has period 1.0s, at what aplitude of motion will the block and piston separate? (b) If the piston has an amplitude of 3.0cm. What is the maximum frequency for which the block and piston will be in contact continuously ?
View SolutionSuppose that a simple pendulum consists of a small 60.0g bob at the end of a cord of negligible mass. If the angle `theta` between the cord and the vertical is given by
`theta= (0.0800 "rad") cos [(6.80 "rad"//s) t + phi]` what are (a) the pendulum's length and (b) its maximum kinetic energy?
View SolutionA block is on a horizontal surface (a shake table) that is moving back and forth horizontally with simple harmonic motion of frequency 2.0 Hz. The coefficient of static friction between block and surface is 0.45. How great can the amplitude of the SHM be if the block is not to slip along the surface?
View Solution
Problems questions and complete solutions for chapter OSCILLATIONS of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12