Complete Solutions to Problems of chapter ELECTRIC CHARGES AND FIELDS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTRIC CHARGES AND FIELDS |
| RESNICK AND HALLIDAY | Problems |
| Number Of Questions | 63 |
| Academic Year | 2023-24 |
In Fig. four particles form a square. The charges are `q_(1) = q_(4) = Q` and `q_(2) = q_(3) = q`. (a) What is Q/q is the net electrostatic force on particles 2 and 3 is zero ? (b) Is there any value of q makes the net electrostatic force on each of the four particles zero ? Explain.

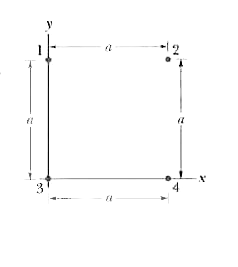
View SolutionIn Fig. , the particles have charges `q_(1) = -q_(2) = 300 nC` and `q_(3) = -q_(4) = 200 n C`, and distance a = 5.0 cm. What are the (a) magnitude and (b) angle (relative to the +x direction) of the net force on particle 3 ?
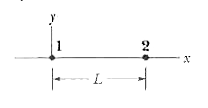
View SolutionIn Fig., particle 1 of charge `+6.0 mu C` and particle 2 of charge `-2.0 mu C` are held at separation `L = 10.0 cm` on an x axis. If particle 3 of unknown charge `q_(3)` is to be located such that the net electrostatic force on it from particles 1 and 2 is zero, what must be the (a) x and (b) y coordinates of particle 3 ?
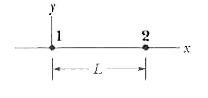
View SolutionThree particles are fixed on an x axis. Particle 1 of charge `q_(1)` is at x = -a, and particle 2 charge `q_(2)` is at x = +a. If their net electrostatic force on particle 3 of charge +Q is to be zero, what must be the ratio `q_(1)//q_(2)` when particle 3 is at (a) x = +0.750 a and (b) x = +1.50 a ?
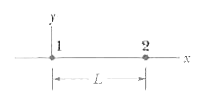
View SolutionIn Fig., particle 1 of charge +q and particle 2 of charge +9.00 q are held at separation L = 8.00 cm on an x axis. If particle 3 of charge `q_(3)` is to be located such that the three particles remain in place when released, what must be the (a) x and (b) y coordinates of particle 3, and (c ) the ratio `q_(3)//q` ?
View SolutionIn Fig., particles 1 and 2 are fixed in place on an axis, at a separation of L = 6.00 cm. Their charges are `q_(1) = +e` and `q_(2) = -27e`. Particle 3 with charge `q_(3) = +4e` is to be placed on the line between particles 1 and 2 , so that they produce a net electrostatic force `vec(F)_("3,net")` on it. (a) At what coordinate should particle 3 be placed to minimize the magnitude of that force ? (b) What is that minimum magnitude ?
View SolutionAs a cat rubs its back along a carpet, it acquires a charge of `+8.2 xx 10^(-7)C`. How many electrons did it lose to the carpet ?
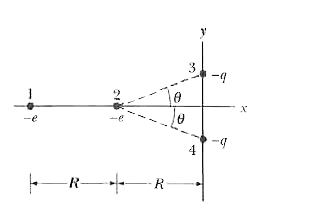
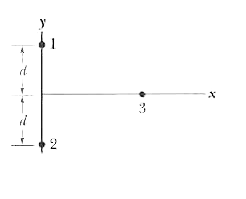
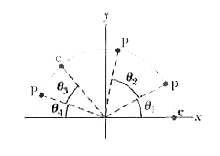
View SolutionFigure shows electrons 1 and 2 on an x axis and charged ions 3 and 4 of identical charge -q and at identical angles `theta`. Electron 2 is free to move, the other three particles are fixed in place at horizontal distances R from electron 2 and are intended to hold electron 2 in place. For physically possible values of `q le 5e`, what are the (a) largest, (b) second largest , and (c ) third largest values of `theta` for which electron 2 is held in place ?
View SolutionThe magnitude of the electrostatic force between point charges `q_(1) = 26.0 mu C` and `q_(2) = 47.0 mu C` is initially 5.70 N. The separation is the changed such that the force magnitude is then 0.570 N. (a) What is the ratio of the new separation to the initial separation ? (b) What is the new separation ?
View SolutionIn the return stroke of a typical lightning bolt, a current of `2.8 xx 10^(4)A` exists for `20 mu s`. How much charge is transferred in this event ?
View SolutionIn Fig., particles 1 and 2 have charge `20.0 mu C` each and are held at separation distance d = 0.75 m. (a) What is the magnitude of the electrostatic force on particle 1 due to particle 2? In Fig., particle 3 of charge `20.0 mu C` is positioned so as to complete an equilateral triangle. (b) What is the magnitude of the net electrostatic force on particle 1 due to particles 2 and 3 ?
View SolutionTwo tiny, spherical water drops, with identical charges of `-1.00 xx 10^(-16)C`, have a center-to-center separation of 1.20 cm. (a) What is the magnitude of the electrostatic force acting between them ? (b) How many excess electrons are on each drop, giving it its charge imbalance ?
View SolutionThe magnitude of the electrostatic force between two identical ions that separated by a distance of `10.0 xx 10^(-10)m` is `9.25 xx 10^(-10)N`. (a) What is the charge of each ion ? (b) How many electrons are "missing" from each ion (thus giving the ion its charge imbalance) ? (c ) What is the force magnitude if the separation is halved ?
View SolutionTwo identical conducting spheres, fixed in place, attract each other with an electrostatic force of 0.108 N when their center-to-center separation is 50.0 cm. The spheres are then connected by a thin conducting wire. When the wire is removed, the spheres repel each other with an electrostatic force of 0.144 N. Of the initial charges on the spheres, with a positive net charge, what was (a) the negative charge on one of them and (b) the positive charge on the other ?
View SolutionTwo equally charged particles, held `3.2xx10^(-3) m` apart, are released from rest. The initial acceleration of the first particle is observed to be `7.0 m//s^(2)` and that of the second to be `9.0 m//s^(2)`. If the mass of the first particle is `6.3xx10^(-7) kg`, what are (a) the mass of the second particle and (b) the magnitude of the charge of each particle ?
View SolutionThe charges and coordinates of two charged particles held fixed in an xy plane are `q_(1) = +3.0 mu C, x_(1) = 3.5 cm, y_(1) = 0.50 cm`, and `q_(2) = -4.0 mu C, x_(2) =-2.0 cm, y_(2) = 1.5 cm`. Find the (a) magnitude and (b) direction of the electrostatic force on particle 1 due to particle 2. At what (c ) x and (d) y coordinates should a third particle of charge `q_(3) = +6.0 mu C` be placed such that the net electrostatic force on particle 1 due to particles 2 and 3 is zero ?
View SolutionIn Fig., particles 2 and 4, of charge -e are fixed in place on a y axis, at `y_(2) = -10.0 cm` and `y_(4) = 5.00 cm`. Particles 1 and 3, of charge -e can be moved along the x axis. Particle 5, of charge +e, is fixed at the origin. Initially particle 1 is at `x_(1) = -10.0 cm` and particle 3 is at `x_(3) = 10.0 cm` (a) To what x value must particle 1 be moved to rotate the direction of the net electric force `vec(F)_("net")` on particle 5 by `60^(@)` counterclockwise? (b) With particle 1 fixed at its new position, to what x value must you move particle 3 to rotate `vec(F)_("net")` back to its original direction ?
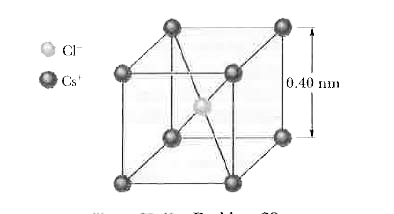
View SolutionIn crystals of the salt cesium, cesium ions `Cs^(+)` form the eight corners of a cube and a chlorine ion `Cl^(-)` is at the cube's center Fig. The edge length of the cube is 0.40 nm. The `Cs^(+)` ions are each deficient by one electron (and thus each has a charge of -e), and the `Cl^(-)` ion has one excess electron (and thus has a charge of -e). (a) What is the magnitude of the net electrostatic force exerted on the `Cl^(-)` ion by the eight `Cs^(+)` ions at the corners of the cube? (b) If one of the `Cs^(+)` ions is missing, the crystal is said to have a defect, what is the magnitude of the net electrostatic force exerted on the `Cl^(-)` ion by the seven remaining `Cl^(+)` ions ?
View SolutionTwo particles are fixed on an x axis. Particle 1 of charge `50 mu C` is located at x = - 20.0 cm, particle 2 of charge Q is located at x = 3.0 cm. Particle 3 of charge magnitude `20 mu C` is released from rest on the y axis y = 2.0 cm. What is the value of Q if the initial acceleration of particle 3 is in the positive direction of (a) the x axis and (b) the y axis ?
View SolutionIn Fig., particles 1 and 2 of charge `q_(1) = q_(2) = +4e` are on a y axis at distance d = 1.70 m from the origin. Particle 3 of charge `q_(3) = +8e` is moved gradually along the x axis from x = 0 to x = +5.0 m. At what values of x will the magnitude of the electrostatic force on the third particle from the other two particles be (a) minimum and (b) maximum ? What are the (c ) minimum and (d) maximum magnitudes ?
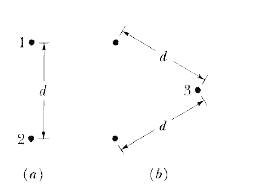
View SolutionIn Fig. a, particle 1 (of charge `q_(1)`) and particle 2 (of charge `q_(2)`) are fixed in place on an x axis, `8.00` cm apart.

Particle 3 (of charge `q_(3)=+8.00xx10^(-19)C`) is to be placed on the line between particles 1 and 2 so that they produce a net electrostatic force `F_("net")=2F_(0)` on it Figure b gives the x component of that force versus the coordinate x at which particle 3 is placed. The scale of the x-axis is set by `x_(s)=8.0`cm. What are (a) the sign of charge `q_(1)` and (b) the ratio `q_(2)//q_(1)`?
View SolutionA particle of charge `3.00 mu C` is separated by 0.120 m from a particle of charge `-1.50 mu C`. (a) What is the magnitude of the electrostatic force between them ? (b) What must their separation be to reduce that force by an order of magnitude ?
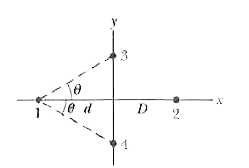
View SolutionFigure shows an arrangement of four charged particles, with angle `theta = 35.0^(@)` and distance d = 2.00 cm. Particle 2 has charge `q_(2) = +8.00 xx 10^(-19) C`, particle 3 and 4 have charges `q_(3) = q_(4) = -1.60 xx 10^(-19)C`, (a) What is distance D between the origin and particle 2 if the net electrostatic force on particle 1 due to the other particles is zero ? (b) If particles 3 and 4 were moved closer to the x axis but maintained their symmetry about that axis, would the required value of D be greater than, less than, or the same as the part (a) ?
View SolutionIn Fig., three charged particles lie on an x axis. Particles 1 and 2 are fixed in place. Particle 3 is free to move, but the net electrostatic force on it from particles 1 and 2 happens to be zero. If `2.0 L_(23) = L_(12)`, what is the ratio `q_(1)//q_(2)` ?
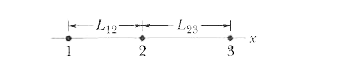
View SolutionTwo charged particles are fixed to an x axis : Particle 1 of charge `q_(1) = 2.1 xx 10^(-8) C` is at position x = 20 cm and particle 2 of charge `q_(2) = -4.00 q_(1)` is at position x = 70 cm. (a) At what coordinate on the axis (other than at infinity) is the net electric field produced by the two particles equal to zero ? (b) What is the zero-field coordinate if the particles are interchanged ?
View SolutionAt what distance along the central perpendicular axis of a uniformly charged plastic disk of radius 0.600 m is the magnitude of the electric field equal to 25% of the magnitude of the field at the center of the surface of the disk ?
View SolutionAssume that a honeybee is a sphere of diameter 1.000 cm with a charge `+ 60.0 pC` uniformly spread over its surface . Assume also that a spherical pollen grain of diameter `40.0 mu C` is electrically held on the surface of the bee because the bee's charge induces a charge of `1.00 pC` on the near side of the grain and a charge of `1+1.00 pC` on the far side. (a) what is the magnitude of the net electrostatic force on the grain due to the bee ? Next, assume that the bee brings the grain to a distance of 1.000 mm from the tip of a flower's stigma and that the tip is a particle of charge `-60.0 pC`. (b) What is magnitude of the net electrostatic force on the grain due to the stigma ? (c ) Does the grain remain on the bee or move to the stigma ?
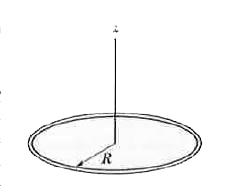
View SolutionA thin nonconducting rod with a uniform distribution of positive charge Q is bent into a complete circle of radius R (Fig.). The central perpendicular axis through the ring is a z aaxis, with the origin at the center of the ring. What is the magnitude of the electric field due to the rod at (a) z = 0 and (b) `z = oo` ? (c ) In terms of R, at what positive and `Q = 5.00 mu C`, what is the maximum magnitude ?
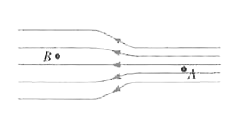
View SolutionTwo large parallel copper plates are 8.0 cm apart and have a uniform electric field between them as depicted in Fig. An electron is released from the negatibe plate at the same time that a proton is released from the positive plate. Neglect the force of the particle on each other and find their distance from the positive plate when they pass each other.
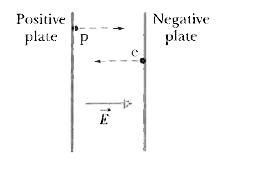
View SolutionFigure shows an uneven arrangement of electrons (e) and protons (p) on a circular arc of radius r = 2.50 cm, with angles `theta_(1) = 30.0^(@), theta_(2) = 50.0^(@), theta_(3) = 30.0^(@)`, and `theta_(4) = 20.0^(@)`. What are the (a) magnitude and (b) direction (relative to the positive direction of the x axis) of the net electric field produced at the net electric field produced at the center of the arc ?
View SolutionIn Fig., positive charge q = 9.25 pC is spread uniformly along a thin nonconducting rod of length L = 16.0 cm. What are the (a) magnitude and (b) direction (relative to the positive direction of the x axis) of the electric field produced at point P, at distance R = 6.00 cm from the rod along its perpendicular bisector ?

View SolutionIn Fig., two curved plastic rods, one of charge +q and the other of charge -q form a circle of radius R = 4.25 cm in an xy plane. The x axis passes through both of the connecting points and the charge is distributed uniformly on both rods. If q = 15.0 pC, what are the (a) magnitude and (b) direction (relative to the positive direction of the x axis) of the electric field `vec(E)` produced at P, the center of the circle ?

View SolutionA charged particle creates an electric field of magnitude 300 N/C at a point 0.800 m away. What is the difference in the field magnitude between that point and one at 0.400 m ?
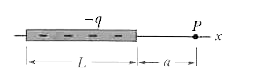
View SolutionIn Fig., a nonconducting rod of length L = 8.15 cm has a charge -q = -4.23 fC uniformly distributed along its length. (a) What is the linear charge density of the rod ? What are the (b) magnitude and (c ) direction (relative to the positive direction of the x axis) of the electric field produced at point P, at distance a = 6.00 cm from the rod ? What is the electric field magnitude produced at distance a = 50 m by (d) the rod and (e) a particle of charge -q = -4.23 fC that we use to replace the rod ? (At that distance, the rod "looks" like a particle.)
View SolutionIn Fig., a thin rod forms a semicircle of radius r = 3.00 cm. Charge is uniformly distributed along the rod, with +q = 4.50 pC in the upper half and -q = -4.50 pC in the lower half. What are the (a) magnitude and (b) direction (relative to the positive direction of the x axis) of the electric field `vec(E)` at P, the center of the semicircle ?

View SolutionTwo charged particles are attached to an x axis: Particle 1 of charge `-4.00 xx 10^(-7) C` is at position x = -5.00 cm and particle 2 of charge `+4.00 xx 10^(-7)C` is at position x = 10.cm. Midway between the particles, what is their net electric field in unit-vector notation ?
View SolutionIn Fig., the four particles form a square of edge length a = 5.00 cm and have charges `q_(1) = +3 nC, q_(2) = -15 nC, q_(3) = +15 nC`, and `q_(4) = -30 nC`. In unit-vector notation, what net electric field do the particles produce at the square's center ?

View SolutionAn electron with a speed of `2.60 xx 10^(8) cm//s` enters and electric field of magnitude `1.00 xx 10^(3)N//C`, travelling along a field in the direction that retards its motion. (a) How far will the electron travel in the field before stopping momentarily, and (b) how much time will have elapsed ? (c ) If the region containing the electric field is 8.00 mm long (too short for the electroc to stop within it),what fraction of the electrons initial energy will be lost in that region ?
View SolutionAn electron is released from rest on the axis of an electric dipole is 25 nm from the center of the dipole. What is the magnitude of the electron's acceleration if the dipole moment is `3.6 xx 10^(-29)C.m`? Assume that 25 nm is much larger than the separation of the charged particles that form the dipole ?
View SolutionIn Fig. the electric field lines on the left have twice the separation of those on the right. (a) If the magnitude of the field at A is 60 N/C, what is the magnitude of the force on a protorn at A? (b) What is the magnitude of the field at B?
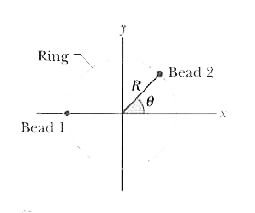
View SolutionFigure shows a distance ring of radius R = 43.0 cm. Two small charged beads are on the ring : Bead 1 of charge `+20.0 mu C` is fixed in place at the left side , bead 2 of charge `+6.00 mu C` can be moved along the ring. The two beads produce a net electric field of magnitude e at the center of the ring. At what (a) positive and (b) negative value of angle `theta` should bead 2 be positioned such that `E= 2.00 xx 10^(5) N//C` ?
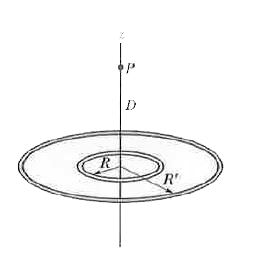
View SolutionFigure shows two concentric rings, of radii R and R' = 4.00 R, that lie on the same plane. Point P lies on the central z axis, at distance D = 2.00 R from the center of the rings. The smaller ring has uniformly distributed charge +Q. In terms of Q, what is the uniformly distributed charge on the larger ring if the net electriv field at P is zero ?
View SolutionA circular plastic disk with radius R = 2.00 cm has a uniformly distributed charge `Q = + (2.00 xx 10^(6))e` on one face. A circular ring of width `40 mu m` is centers on that face, with the center of that width at radius r = 0.50 cm. In coulombs, what charge is contained within the width of the ring ?
View SolutionCharge is uniformly distributed around a ring of radius R = 4.60 cm, and the resulting electric field magnitude R is measured along the ring's central axis (perpendicular to the plane of the ring). At what distance from the ring's center is E maximum ?
View SolutionIn Fig., the three particles are fixed in place and have charges `q_(1) = q_(2) = +5e` and `q_(3) = +2e`. Distance `a = 3.00 mu m`. What are the (a) magnitude and (b) direction of the net electric field at point P due to the particles ?
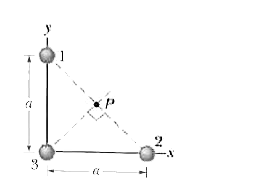
View SolutionIn Fig., the four particles fixed in palce and have charges `q_(1) = q_(2) = +5e, q_(3) = +3e` and `q_(4) = -1e`. Distance `d = 8.0 mu m`. What is the magnitude of the net electric field at point P due to the particles ?

View SolutionAn electric dipole consisting of charges of magnitude `1.50 nC` separated by 6.20 `mu m` is in an electric field of strength 300 N/C. what are (a) the magnitude of the electric dipole moment and (b) the difference between the potential energies for dipole orientations parallel and perpendicular to `vec(E)` ?
View SolutionAn electron is released from rest in a uniform electric field of magnitude `2.00 xx 10^(4) N//C` . (a) Calculate the acceleration of the electron. (Ignore gravitational) (b) How much time does the electron take to reach 1.00 % of the speed of light ?
View SolutionAn electron enters a region of uniform electric field with an initial velocity of 30 km/s in the same direction as the electric field, which has magnitude E = 50 N/C. (a) What is the speed of the electron 1.5 ns after entering this region? (b) How far does the electron travel during the 1.5 ns interval ?
View SolutionA uniform electric field exists in a region between two oppositely charged plates. An electron is released from rest at the surface of the negatively charged plate and strikes the surface of the opposite plate, 3.0 cm away, in a time `1.5 xx 10^(-8) s`. Just as the electron strikes the second plate, what are the its (a) momentum magnitude and (b) kinetic energy ? (c ) What is the magnitude of the electric field `vec(E)` ?
View SolutionAn electric dipole consists of charges `+ 2e and -2e` separated by 0.78mm. It is an electric field of strength `3.4xx10^(6) N//C`. Calculate the magnitude of the torque on the dipole when the dipole moment is (a) parallel to (b) perpendicular to, and (c) anti-parallel to the electric field.
View SolutionAt some instant the velocity components of an electron moving between two charged parallel plates are `v_x=1.5xx10^5m//s` and `v_y=3.0xx10^6 m//s`.Suppose that the electric field between the plates is given by `E = (120 N//C) hatj`
. (a) What is the acceleration of the electron?
(b) What will be the velocity of the electron after its x-coordinate has changed by 2.0 cm?
View SolutionA charged particles produces an electric field with a magnitude of 2.0 N/C at a point that is 50 cm away from the particle. What is the magnitude of the field at an additional distance of 2.5 cm ?
View SolutionIn Fig. a "semi-infinite" nonconducting rod (that is, infinite in one direction only) has uniform linear charge density `lambda`. (a) show that the electric field `vec(E)_(p)`at point P makes an angle `45^(@)` with the rod and that this result is independent of the distance R. (Hint : Separetly find the component of `vec(E)_(p)` parallel to the rod and the component perpendicular to the rod.) (b) Find the the field magnitude for linear charge density 4.52 nC/m and R = 3.80 cm.

View SolutionFigure shows two charged particles on an x axis : `-q = -3.20 xx 10^(-19)C` at `x = -3.00m` and `q = 3.20 xx 10^(-19)C` at = + 3.00 m. What are (a) magnitude and (b) direction (relative to the positive direction of the x axis) of the net electric field produced at point P at y = 4.00 m? (c ) What is the magnitude of the net field if y is doubled ?

View SolutionIn Fig. an electron (e) is to be released from rest on the central axis of a uniformly charged disk of radius R. The surface charge density on the disk is `+5.00 mu C//m^(2)`. What is the magnitude of the electron's initial acceleration if it is released at a distance (a) R, (b) R/100, and (c ) R/1000 from the center of the disk ? (d) Why does the acceleration magnitude increase only slightly as the release point is moved closer to the disk ?
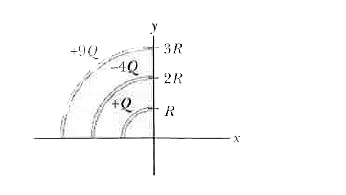
View SolutionFigure shows the three circular arcs centered on the origin of a coordinate system. On each arc, the uniformly distributed charge is given in terms of `Q = 4.00 mu C`. The radii are given in terms of R = 5.00 cm. What are the (a) magnitude and (b) direction (relative to the positive x direction) of the net electric field at origin due to the arc ?
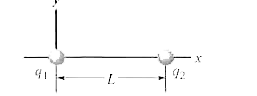
View SolutionTwo charged particles lie along x axis as shown in Fig. The particle with charge `q2 = +8 mu C` is at x = 6.00 m, and the particle with charge `q1 = +2 mu C` is at the origin. Locate the point where the resultant electric field is zero.
View SolutionIn the situation described in Problem 63, find the condition that a charge kept on x = 2m may be in a stable equilibrium. If the charge is of magnitude `1 mu C` and has a mass of 3 g, find the time period of small oscillations of the body from its equilibrium position.
View SolutionA semi-infinite charged rod is arranged so that its one end coincides with the center of a charged ring as shown in Fig. Both of them have a charge per unit length of `lambda.` The radius of ring is R. The electric field of rof exert force on an element of the ring as shown in Fig. (a) What is the force on the ring due to the rod ? (b) What is the increase in the tension of the ring due to the rod ?
View SolutionA positive charge q is placed in front of a conducting solid body at a distance d from its center. (a) Find the electric field at the center of the cube due to the charges appearing on its surface. (b) Does the body have to be spherical for the answer to be true ?
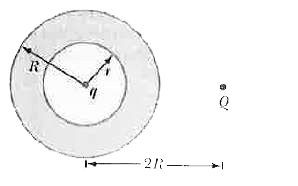
View SolutionA conducting spherical shell of outer radius R and inner radius r = 3R/4 has no net charge on it. At its center there is a point charge q, and at a distance 2R from its center there is a point charge Q (Fig.) . (a) What is the magnitude of the electrostatic force on the charge q at the center due to the shell ? (b) What is the magnitude of net force on it?
View SolutionA pellet with charge +Q is centered inside a spherical cavity in a conducting ball. The conducting ball has a charge -2q on it. The cavity in the ball is off-center, as shown in Fig. (a) How much charge resides on the inner surface of the cavity ? (b) Is the charge on the cavity surface distributed uniformly or nonuniformly ? Why ? (c ) How much charge resides on the outer surface of the conducting ball ? (d) Is the charge on the ball's outer surface distribution uniformly or nonuniformly ?
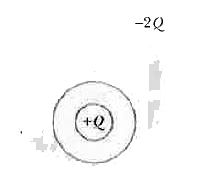
View Solution
Problems questions and complete solutions for chapter ELECTRIC CHARGES AND FIELDS of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12