Complete Solutions to साधित उदाहरण of chapter समांतर चतुर्भुज व त्रिभुज के क्षेत्रफल of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | समांतर चतुर्भुज व त्रिभुज के क्षेत्रफल |
| BALAJI PUBLICATION | साधित उदाहरण |
| Number Of Questions | 21 |
| Academic Year | 2023-24 |
चित्र में ABCD एक चतुर्भुज है तथा BD इसका एक विकर्ण है । सिद्ध कीजिए कि ABCD एक समांतर चतुर्भुज है तथा इसका क्षेत्रफल ज्ञात कीजिए।
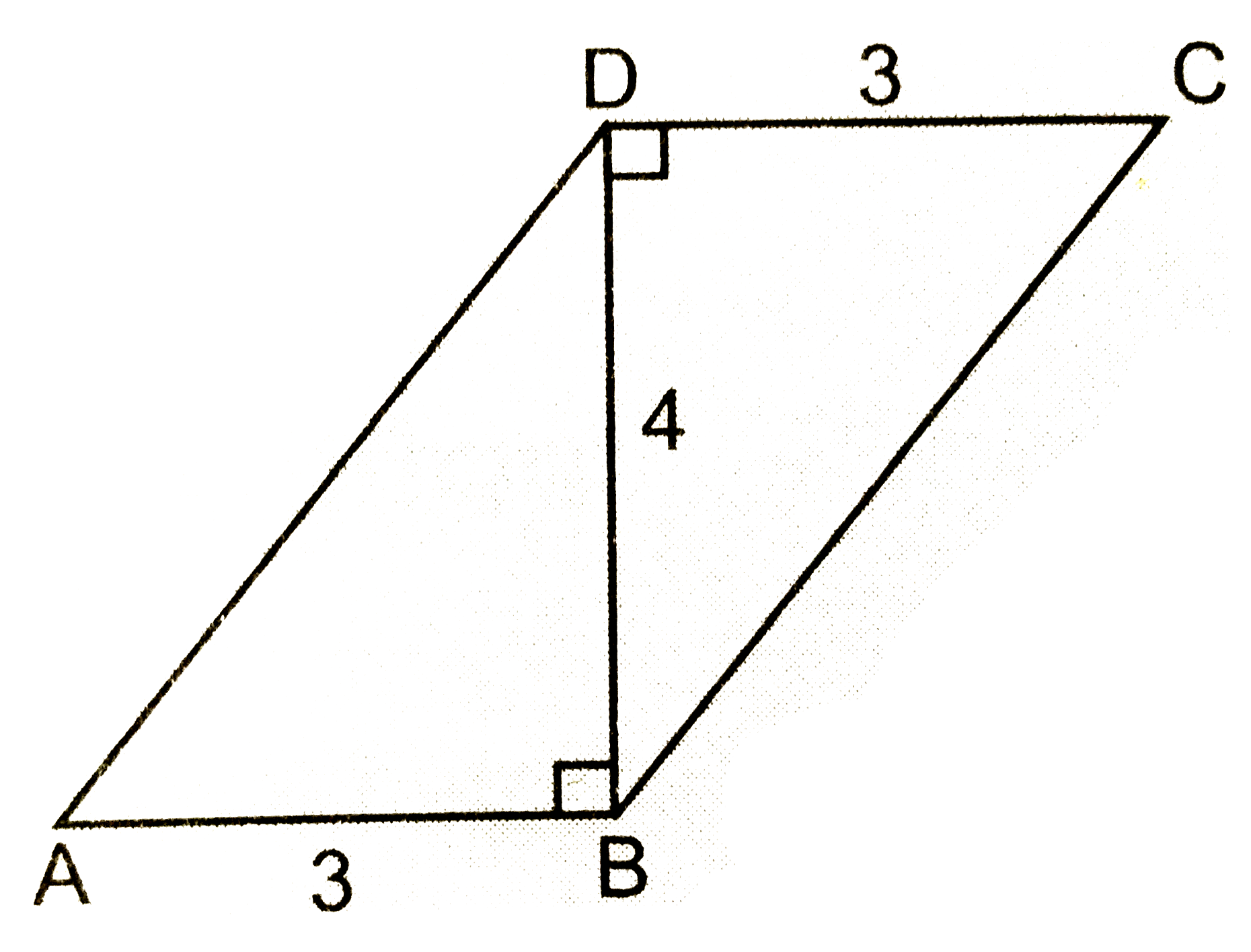
View Solutionएक समांतर चतुर्भुज ABCD में `AB=8` सेमी है। भुजाएं AB व AD के संगत शीर्षलम्ब क्रमशः 4 व 5 सेमी हैं। AD का मान ज्ञात कीजिए।
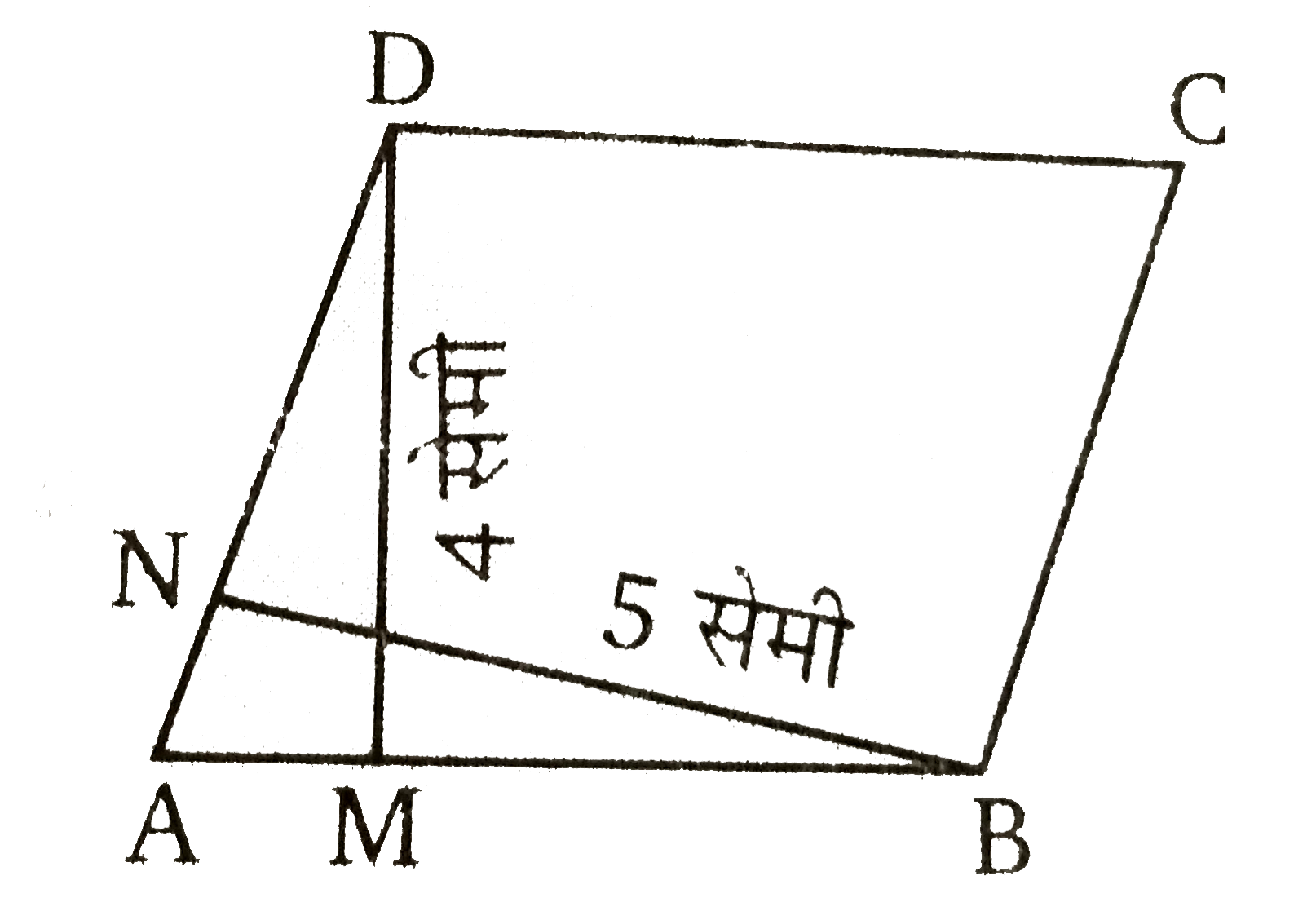
View Solution`AD,Delta ABC` की माध्यिकाओं में से एक है तथा `O,AD` का कोई बिंदु है। सिद्ध कीजिए कि `ar(DeltaABO)=ar(DeltaACO)`।
View Solutionसिद्ध कीजिए कि दी हुई भुजाओं वाले सभी समांतर चतुर्भुजों में सबसे अधिक क्षेत्र वाला समांतर चतुर्भुज एक आयत होता है।
View Solutionएक आयत `ABCD` का क्षेत्रफल `50` वर्ग सेमी है यदि `AB` पर कोई बिंदु `P` है तब `DeltaPCD` का क्षेत्रफल ज्ञात कीजिए।
View Solutionयदि `DeltaABC` का केंद्र `G` है तो सिद्ध कीजिए कि `DeltaGAB` का क्षेत्रफल `= 1/3 DeltaABC` का क्षेत्रफल
View Solutionउस समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसका क्षेत्रफल, आधार तथा संगत शीर्षलम्ब क्रमशः `x^(2)`, `x-3` व `x+4` है।
View SolutionABC एक त्रिभुज है तथा `AD` इसकी एक माध्यिका है यदि `X,AD` पर कोई बिंदु है तब सिद्ध कीजिए कि
`ar(DeltaABX)=ar(DeltaACX)`
View Solutionसमांतर चतुर्भुज `ABCD` में `AB=16` सेमी तथा `AB` व `AD` भुजाओं के संगत शीर्षलम्ब क्रमशः `8` सेमी व `10` सेमी हैं, तो `AD` का मान ज्ञात कीजिए।
View Solution`DeltaABC` में `AB=8` सेमी तथा AB के संगत शीर्षलम्ब 5 सेमी है `Delta DEF` में `EF=10` सेमी। यदि `ar(Delta ABC)=ar(Delta DEF)` तब `EF` के संगत शीर्षलम्ब ज्ञात कीजिए।
View Solutionमाना ABC व DBC समान आधार BC पर दो त्रिभुज हैं। BC की विपरीत दिशा से A व D बिंदु इस प्रकार हैं कि `ar(DeltaABC)=ar(DeltaDBC)`। सिद्ध कीजिए यह `BC,AD` को समद्विभाजित करती है।
View Solution`DeltaABC` में `D` भुजा AB का मध्य बिंदु है तथा `P,BC` पर कोई बिंदु है `CQ||PD,AB` के बिंदु `Q` पर मिलती है। सिद्ध कीजिए कि `ar(DeltaBPQ)=1/2ar(DeltaABC)`
View Solutionचित्र में समांतर चतुर्भुज ABCD में भुजा AB को बढ़ाकर बिंदु `P` प्राप्त करते हैं तथा A से एक रेखा CP के समांतर जो CB को बढ़ाकर बिंदु `Q` से मिलती है। इस प्रकार समांतर चतुर्भुज `BQRP` पुरा होता है । सिद्ध कीजिए कि
`ar("समांतर चतुर्भुज ABCD)=ar("समांतर चतुर्भुज" BQRP)`
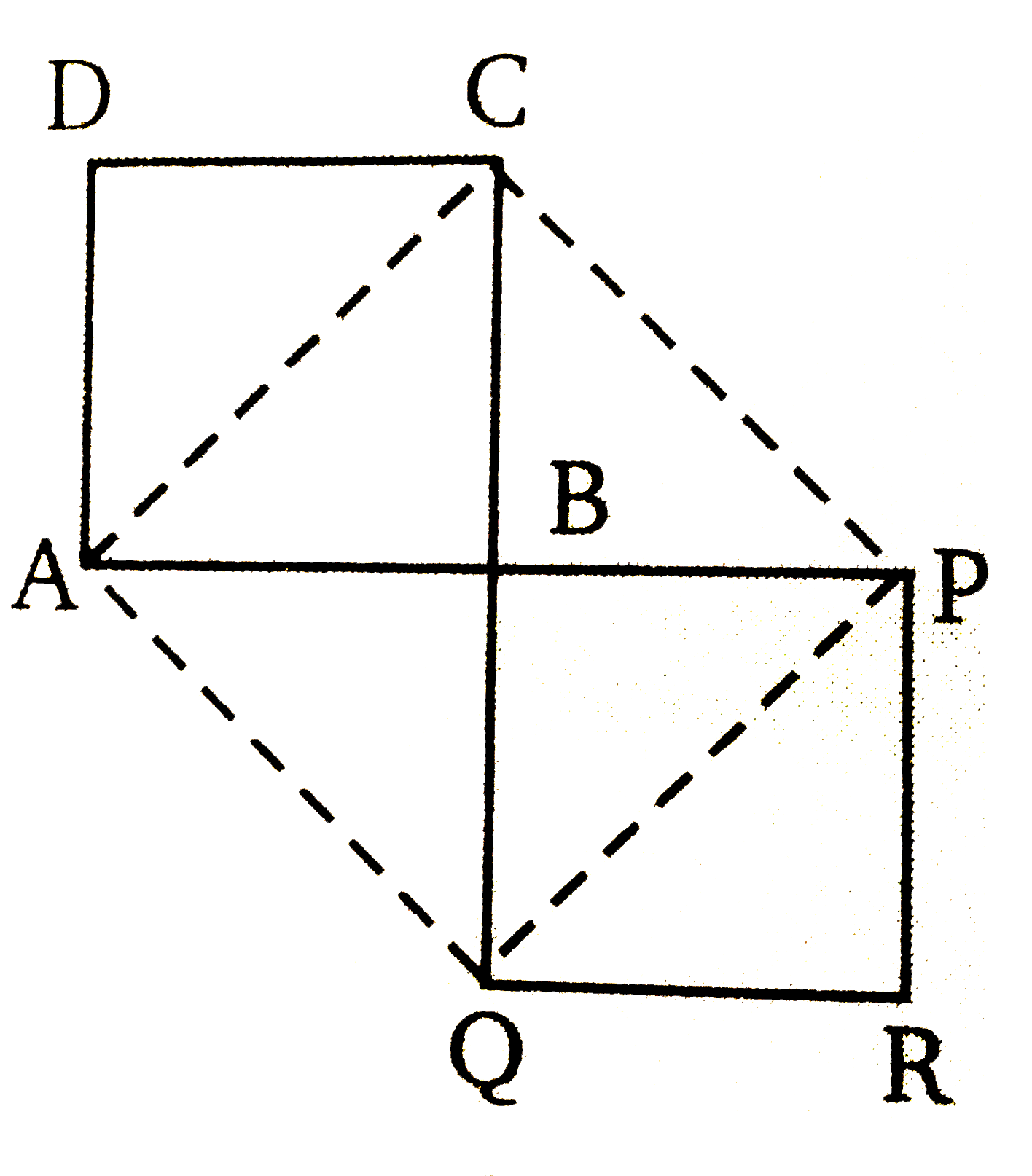
View Solutionएक समांतर चतुर्भुज `ABCD` में E,F,G व H क्रमशः भुजाओं `AB,BC,CD` व `DA` के मध्य बिंदु हैं। सिद्ध कीजिए कि `EFGH` एक समांतर चतुर्भुज होगा तथा इसका क्षेत्रफल ABCD के क्षेत्रफल से आधा होगा।
View Solution`ABCD` एक समांतर चतुर्भुज है तथा `P` इसका कोई अंतः बिंदु है सिद्ध कीजिए कि `DeltaABP` का क्षेत्रफल `+DeltaDCP` का क्षेत्रफल `=1/2` समांतर चतुर्भुज ABCD का क्षेत्रफल
View Solutionएक आयत व एक समांतर चतुर्भुज का क्षेत्रफल बराबर व आधार उभयनिष्ठ है। सिद्ध कीजिए कि आयत का परिमाप समांतर चतुर्भुज के परिमाप से कम होता है।
View Solutionदो त्रिभुजों ABC व DBC के आधार समान हैं तथा सम्मुख भुजा BC पर शीर्ष A व D इस प्रकार हैं कि `ar(DeltaABC)=ar(DeltaDBC)`। सिद्ध कीजिए कि `BC`, रेखा `AD` को समद्विभाजित करती है।
View Solutionसंलग्न चित्र में एक समांतर चतुर्भुज ABCD है तथा BC पर कोई बिंदु `P` है तो सिद्ध कीजिए कि:
`(DeltaABP)` का क्षे0 `+(DeltaDPC)` का क्षे0 `=(DeltaPDA)` का क्षे0
View Solutionसंलग्न चित्र में एक बिंदु `P` एक समांतर चतुर्भुज ABCD का अंतः बिंदु है तो दर्शाइए कि
(i) `(DeltaAPB)` का क्षे0 `+(Delta PCD)` का क्षे0
`=1/2`(समांतर चतुर्भुज ABCD) का क्षे0
(ii) `(DeltaAPD)` का क्षे0 `+(DeltaPBC)` का क्षे0
`=(DeltaAPB)` का क्षे0 `+(DeltaPCD)` का क्षे0

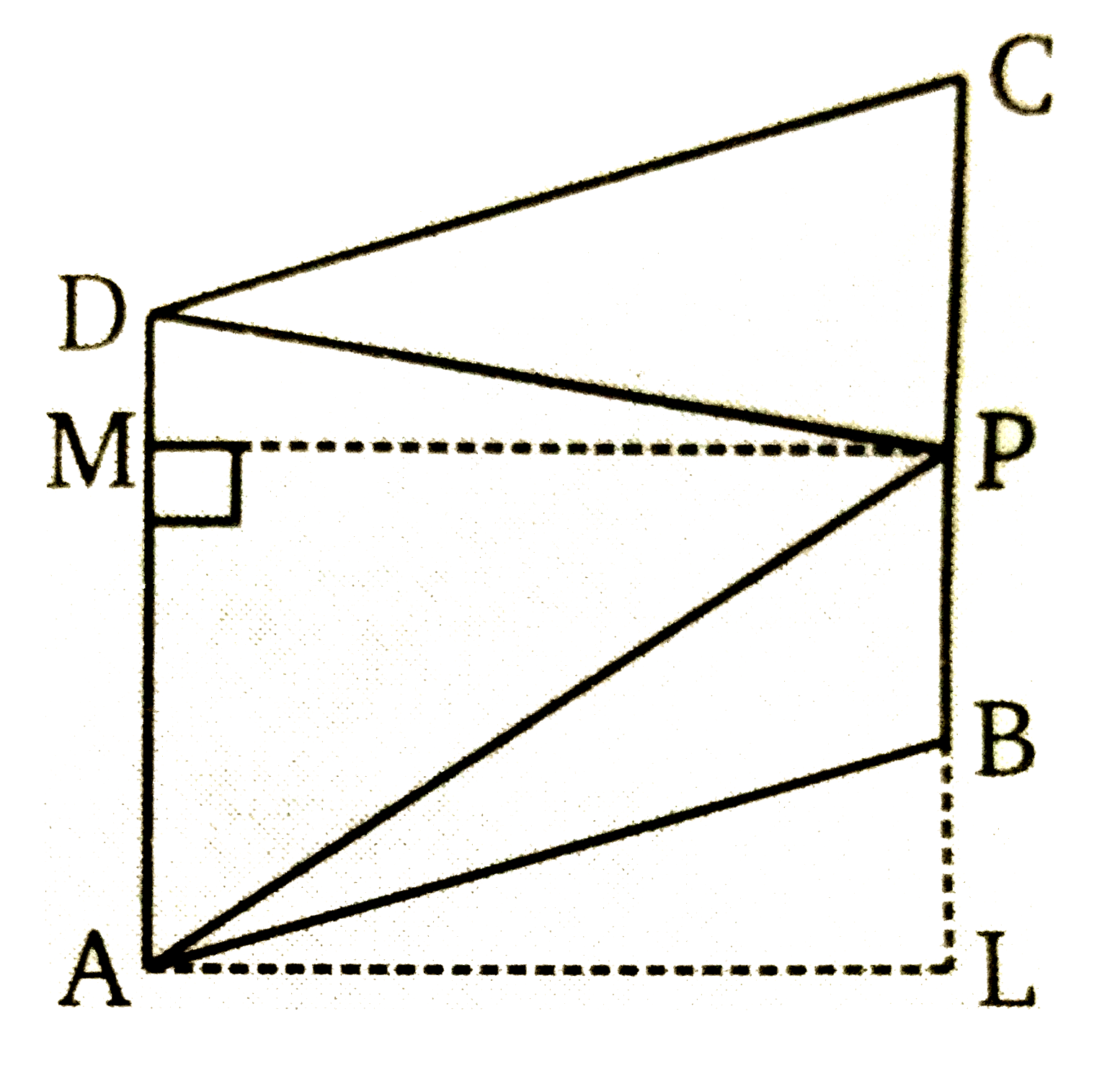
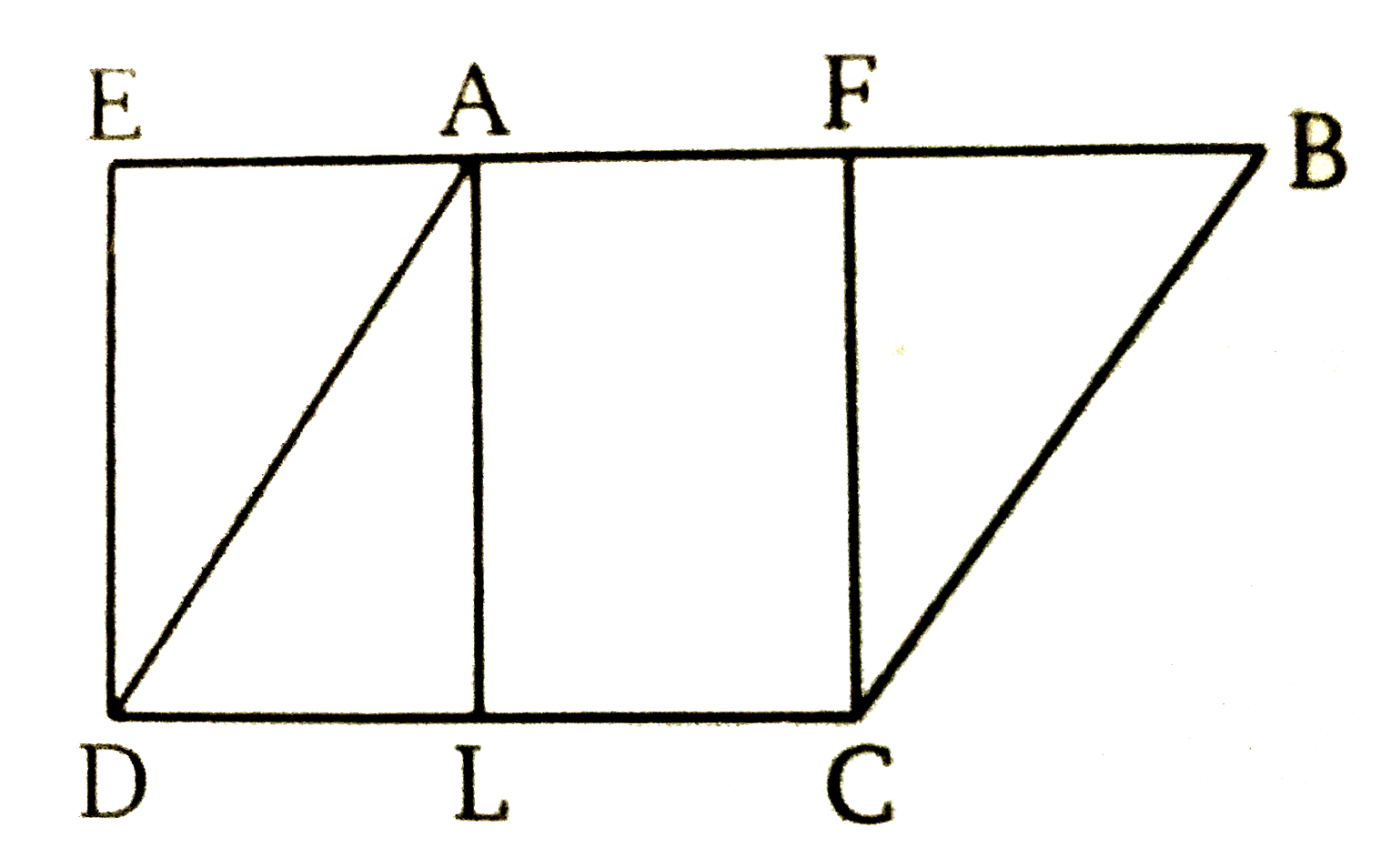
View Solutionसंलग्न चित्र में एक समांतर चतुर्भुज ABCD है तथा एक आयत EFCD है । तथा `AL_|_DC` तो दिखाइए कि-
(i) `(ABCD)` का क्षे0 `=(EFCD)` का क्षे0
(ii)`(ABCD)` का क्षे0 `=DCxxAL`
View Solutionसंलग्न चित्र में एक चतुर्भुज ABCD है और `BE||AC` तथा BE,DC के बढ़े हुए भाग E पर मिलती है तो दर्शाइए कि `DeltaADE` का क्षेत्रफल, चतुर्भुज `ABCD` के क्षेत्रफल के बराबर है।
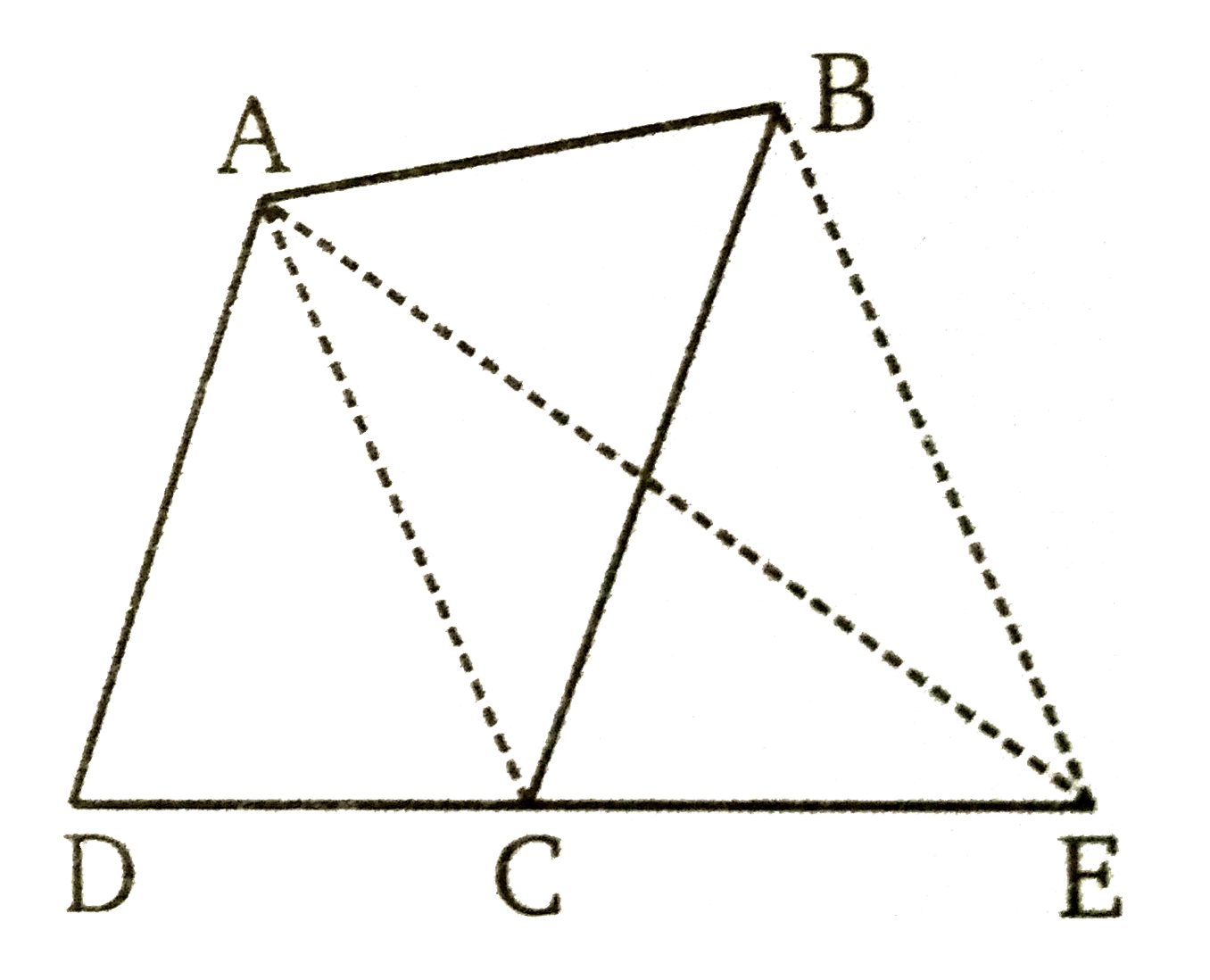
View Solution
साधित उदाहरण questions and complete solutions for chapter समांतर चतुर्भुज व त्रिभुज के क्षेत्रफल of SHREE BALAJI MATHS (HINDI) of Class 9