Complete Solutions to EXERCISE (Assertion & Reason Type ) of chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREAS OF PARALLELOGRAMS AND TRIANGLES |
| MTG IIT JEE FOUNDATION | EXERCISE (Assertion & Reason Type ) |
| Number Of Questions | 5 |
| Academic Year | 2023-24 |
ABCD is a quadrilateral whose diagonals AC divides it into two parts, equal is area. Then, ABCD is
View SolutionAssertion : If the diagonals of a rhombus are 8 cm and 12 cm, then the area of rhombus is given by 96 `cm^(2)`.
Reason : Area o f rhombus is 1/2 `xx d_(1) xx d_(2)` where `d_(1)` and `d_(2)` are the lengths of the diagonals.
View SolutionAssertion : In a parallelogram PQRS, QS is one of the diagonals then ar(`Delta`PQS) = ar(`Delta`QRS)
Reason : If a planar region formed by a figure R is made up of two no noverlapping planar regions formed by figures `R_(1)` and `R_(2)`, then ar(R) = ar(`R_(1)`) + ar(`R_(2)`).
View SolutionAssertion : If area of `Delta`ABD is equal to 24 `cm^(2)` then a rea of p arallelogram ABCD is 24 `cm^(2)`

Reason : If a triangle and a parallelogram are on the same base and between same parallels, then area of the triangle is equ al to h alf of the parallelogram.
View SolutionAssertion : In the given fig ure, the point D divides the side BC of `/_\ABC` in the ratio `m : n`, then ratio of `ar(ABD)` and `ar(ADC)` is `m:n`
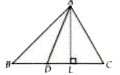
Reason : Area of triangle = 1/2 `xx` Base `xx` Height
View Solution
EXERCISE (Assertion & Reason Type ) questions and complete solutions for chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of MTG IIT JEE FOUNDATION of Class 9
All Exercises from MTG IIT JEE FOUNDATION Class 9 MATHS AREAS OF PARALLELOGRAMS AND TRIANGLES
- EXERCISE ( Subjective Problems ) (Long Answer Type )
- EXERCISE ( Subjective Problems ) (Short Answer Type )
- EXERCISE ( Subjective Problems ) (Very Short Answer Type )
- EXERCISE ( Comprehension Type )
- EXERCISE ( Integer/Numerical Value Type )
- EXERCISE ( Multiple Choice Questions )
- EXERCISE (Assertion & Reason Type )
- EXERCISE (Match the Following )
- ILLUSTRATIONS
- NCERT SECTION ( EXERCISE 9.1)
- NCERT SECTION ( EXERCISE 9.2)
- NCERT SECTION ( EXERCISE 9.3)
- NCERT SECTION ( EXERCISE 9.4)
- Olympiad/HOTS Corner
- SOLVED EXAMPLES