Complete Solutions to ILLUSTRATIONS of chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREAS OF PARALLELOGRAMS AND TRIANGLES |
| MTG IIT JEE FOUNDATION | ILLUSTRATIONS |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
In a parallelogram ABCD, AB = 8 cm. The altitudes corresponding to sides AB and AD are 4 cm and 5 cm respectively. Find AD.
View SolutionABCD is a quadrilateral and BD is one of its diagonals, as shown in the figure. Prove that quadrilateral ABCD is a parallelogram, also find its area.
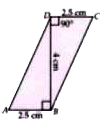
View SolutionShow that the segment joining the mid-points of a pair of opposite sides of a parallelogram, divides it into two equal parallelograms.
View SolutionProve that of all parallelograms of which the sides are given, the parallelogram which is rectangle has the greatest area.
View SolutionShow that a median of a triangle divides it into two triangles of equal areas.
View SolutionIn Figure, `A B C D` is a quadrilateral and `B E|A C` and also `B E` meets `D C` produced at `Edot` Show that area of ` A D E` is equal to the area of the quadrilateral `A B C D`
View SolutionThe diagonals of quadrilateral ABCD, AC and BD intersects at O. Prove that if BO = OD then the triangles ABC and ADC are equal in area.
View SolutionThe area of a trapezium is half the product of its height and sum of parallel sides.
View Solution
ILLUSTRATIONS questions and complete solutions for chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of MTG IIT JEE FOUNDATION of Class 9
All Exercises from MTG IIT JEE FOUNDATION Class 9 MATHS AREAS OF PARALLELOGRAMS AND TRIANGLES
- EXERCISE ( Subjective Problems ) (Long Answer Type )
- EXERCISE ( Subjective Problems ) (Short Answer Type )
- EXERCISE ( Subjective Problems ) (Very Short Answer Type )
- EXERCISE ( Comprehension Type )
- EXERCISE ( Integer/Numerical Value Type )
- EXERCISE ( Multiple Choice Questions )
- EXERCISE (Assertion & Reason Type )
- EXERCISE (Match the Following )
- ILLUSTRATIONS
- NCERT SECTION ( EXERCISE 9.1)
- NCERT SECTION ( EXERCISE 9.2)
- NCERT SECTION ( EXERCISE 9.3)
- NCERT SECTION ( EXERCISE 9.4)
- Olympiad/HOTS Corner
- SOLVED EXAMPLES