Complete Solutions to SOLVED EXAMPLES of chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREAS OF PARALLELOGRAMS AND TRIANGLES |
| MTG IIT JEE FOUNDATION | SOLVED EXAMPLES |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.

View SolutionCompute the area of quadrilateral ABCD.

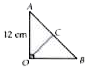
View SolutionIn the given figure `angleAOB`= 90°, AC= BC, OA = 12 cm and OC = 6.5 cm. Find the area of `triangleAOB`.
View SolutionPQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm and A is any point on PQ. If PS = 5 cm, then ar `(DeltaPAS) = `.
View SolutionP is any point on the diagonal BD of the parallelogram ABCD. Prove that ar`(triangleAPD)` = ar`(triangleCPD)`.
View SolutionABCD is a quadrilateral. The straight line through C parallel to the diagonal DB intersects AB produced at E. Prove that the ar(quad. ABCD) = ar`(triangleADE)`.

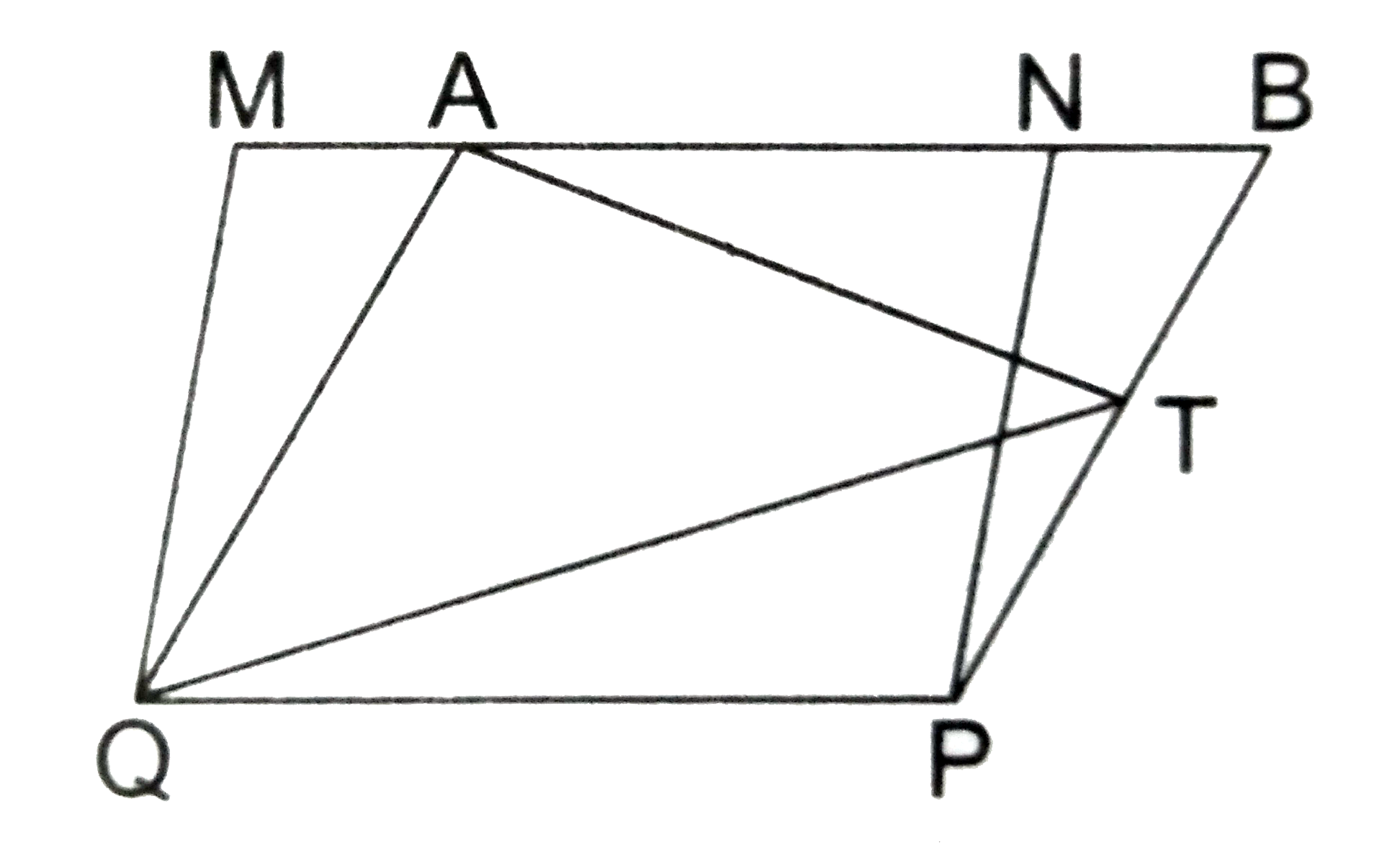
View SolutionIn the adjoining figure, MNPQ and ABPQ are parallelogram and T is any point on the side BP. Prove that
(i) `ar(MNPQ)=ar(ABPQ)`
(ii)` ar(triangleATQ)=(1)/(2)ar(MNPQ)`.
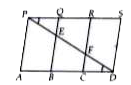
View SolutionIn Figure, `O C D E` is a rectangle inscribed in a quadrant of a circle of radius `10 c mdot` If `O E=2sqrt(5)` , find the area of the rectangle.
View SolutionIf the diagonals `A C ,\ B D` of a quadrilateral `A B C D ,` intersect at `O ,` and separate the quadrilateral into four triangles of equal area, show that quadrilateral `A B C D` is a parallelogram.
View SolutionShow that the area of a rhombus is half the product of the lengths of its diagonals. GIVEN : A rhombus `A B C D` whose diagonals `A C` and `B D` intersect at `Odot` TO PROVE : `a r(r hom b u sA B C D)=1/2(A CxB D)`
View SolutionA point D is taken on the side BC of a `DeltaABC` such that `BD = 2DC.` Prove that `ar(DeltaABD) = 2 ar (DeltaADC)`
View SolutionIn the given figure, `BC||XY, BX||CA and AB ||YC`. Prove that area `(DeltaABX) = area (Delta ACY)`

View SolutionIn the given figure PSDA is a parallelogram in which PQ =QR= RS and AP II BQ II CR II VS.Prove that ar(`trianglePQE`) = ar(`triangleDCF`).
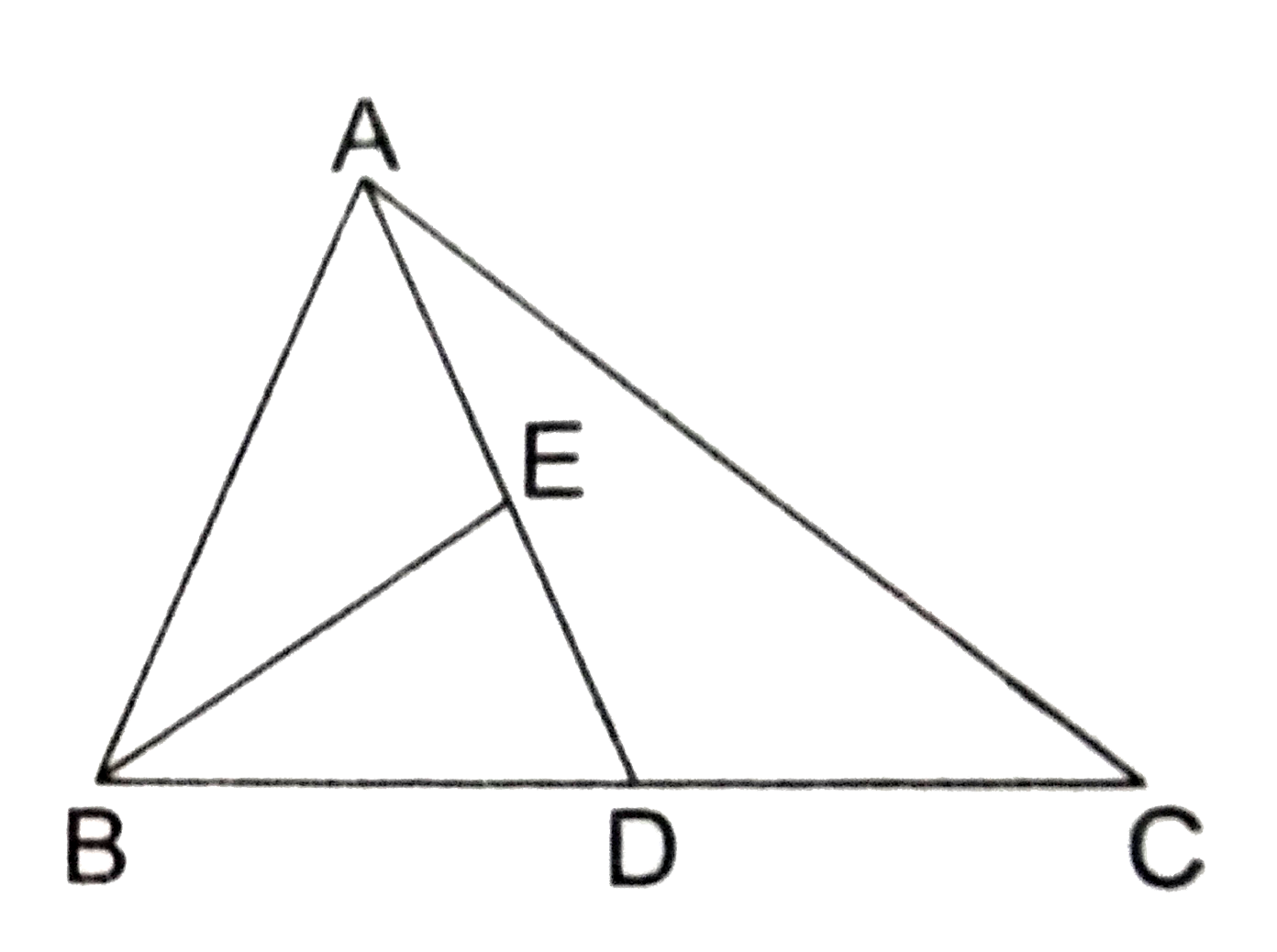
View SolutionABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that `ar(triangleBED)=(1)/(4)ar(triangleABC)`.
View Solution
SOLVED EXAMPLES questions and complete solutions for chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of MTG IIT JEE FOUNDATION of Class 9
All Exercises from MTG IIT JEE FOUNDATION Class 9 MATHS AREAS OF PARALLELOGRAMS AND TRIANGLES
- EXERCISE ( Subjective Problems ) (Long Answer Type )
- EXERCISE ( Subjective Problems ) (Short Answer Type )
- EXERCISE ( Subjective Problems ) (Very Short Answer Type )
- EXERCISE ( Comprehension Type )
- EXERCISE ( Integer/Numerical Value Type )
- EXERCISE ( Multiple Choice Questions )
- EXERCISE (Assertion & Reason Type )
- EXERCISE (Match the Following )
- ILLUSTRATIONS
- NCERT SECTION ( EXERCISE 9.1)
- NCERT SECTION ( EXERCISE 9.2)
- NCERT SECTION ( EXERCISE 9.3)
- NCERT SECTION ( EXERCISE 9.4)
- Olympiad/HOTS Corner
- SOLVED EXAMPLES