Complete Solutions to Olympiad/HOTS Corner of chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREAS OF PARALLELOGRAMS AND TRIANGLES |
| MTG IIT JEE FOUNDATION | Olympiad/HOTS Corner |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
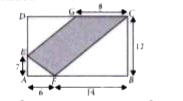
In the given figure ABCD is a rectangle and all measurements are in centimeters. Find the area of the shaded region.
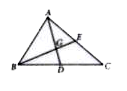
View SolutionIn given `DeltaABC`, AD and BE are medians of triangle which intersect each other at point G. If area of `DeltaBDG` is 1 `cm^2`, then what is the area of DCEG?
View SolutionIf side of a square is increased by 20% then the percentage increase in its area is
View SolutionIf each sides of a triangle is doubled then find the ratio of the area of the new triangle thus formed and the given triangle.
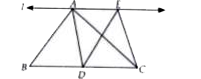
View SolutionIn the given figure, `l || BC` and D is the mid-point of BC. If area `(DeltaABC)` = `a` x area`(DeltaEDC)`, then find the value of a.
View SolutionThe perimeter of the rectangular field is 206 meter. What will be its area (in `m^2`) if its length is 23 meter more than its breadth ?
View SolutionA person walked diagonally across a square plot. Approximately, what was the percentage saved by not walking along the edges?
View SolutionThe perimeter of a right angled triangle is 24 cm. If its hypotenuse is 10 cm then area of this triangle is
View SolutionIn parallelogram ABCD, let AM be the altitude corresponding to the base BC and CN the altitude corresponding to the base AB. If AB = 10 cm, AM = 6 cm and CN = 12 cm, then BC= __ cm.
View SolutionIn triangle ABC,D is the midpoint of AB, E is the midpoint of DB and F is the midpoint of BC. If the area of `DeltaABC` is 96, the area of `DeltaAEF` is
View SolutionIn the figure ABCD is a rectangle with AE = EF = FB, the ratio of the areas of triangle CEF and that of rectangle ABCD is

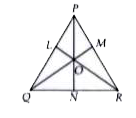
View SolutionIf the medians of `DeltaPQR` intersect at O, then ar `(DeltaPOQ)` =
View SolutionIn the figure, the area of square `ABCD is 4 cm^2` and E any point on AB,F,H and K are the mid point of `DE,CF,DG, and CH` respectively. The area of `DeltaKDC` is -
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line a drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View Solution
Olympiad/HOTS Corner questions and complete solutions for chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of MTG IIT JEE FOUNDATION of Class 9
All Exercises from MTG IIT JEE FOUNDATION Class 9 MATHS AREAS OF PARALLELOGRAMS AND TRIANGLES
- EXERCISE ( Subjective Problems ) (Long Answer Type )
- EXERCISE ( Subjective Problems ) (Short Answer Type )
- EXERCISE ( Subjective Problems ) (Very Short Answer Type )
- EXERCISE ( Comprehension Type )
- EXERCISE ( Integer/Numerical Value Type )
- EXERCISE ( Multiple Choice Questions )
- EXERCISE (Assertion & Reason Type )
- EXERCISE (Match the Following )
- ILLUSTRATIONS
- NCERT SECTION ( EXERCISE 9.1)
- NCERT SECTION ( EXERCISE 9.2)
- NCERT SECTION ( EXERCISE 9.3)
- NCERT SECTION ( EXERCISE 9.4)
- Olympiad/HOTS Corner
- SOLVED EXAMPLES