Complete Solutions to Solved Examples of chapter STATISTICS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | STATISTICS |
| NAGEEN PRAKASHAN | Solved Examples |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
The number of children in the families of a village are listed below :
`1, 2, 1, 1, 2, 2, 2, 3, 2, 2, 2, 4, 1, 2, 3, 2, 2, 1, 1, 0, 0, 1, 2, 0, 1, 2, 0, 1, 2, 2, 2, 2, 1, 2, 3, 3, 4, 2, 1, 2.`
Prepare a frequency distribution table.
View SolutionGiven below are the marks obtained by 30 students of a class, Using the class intervals of equal class size in which one class interval is 30-40 (excluding 40), construct a frequency table.
`{:(42,74,39,48,42,80,35,38,52,81),(31,72,65,58,77,82,79,65,47,30),(64,56,39,48,60,63,72,50,46,35):}`
View SolutionThe marks of `20` students out of `25` are given below
`{:(12,17,22,7,11,19,24,18,4,8),(23,2,5,15,21,16,11,9,12,17):}`
View SolutionThe table given below shows a frequency distribution table, find
(a) Upper limit of third class (b) Lower limit of fifth class
(c) Class size (d) Class mark of third class
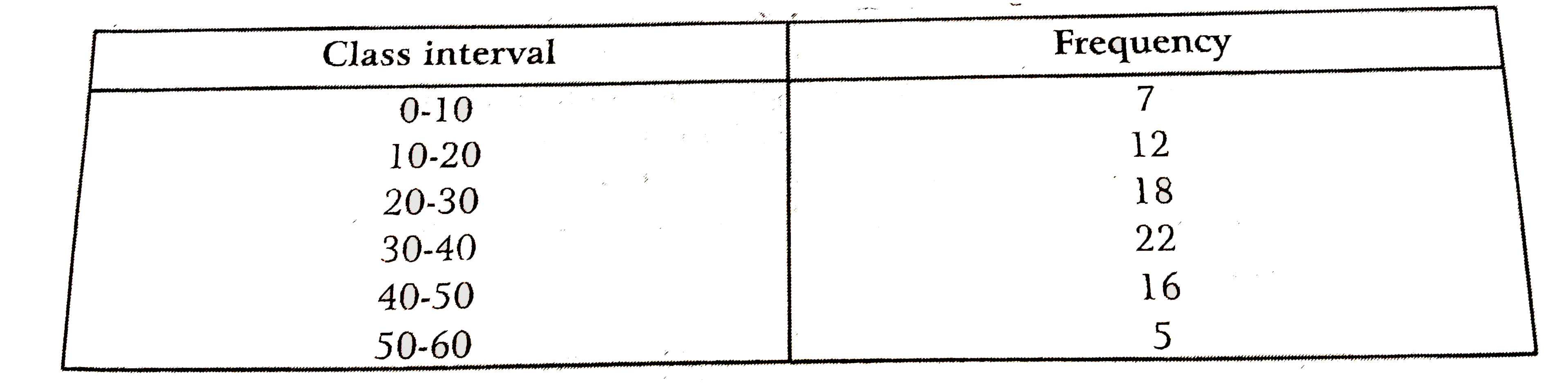
View SolutionThe class marks of a distribution are 61,66,71,76,81,86,91,96,101,106. Determine the class size, class limits and true class limits.
View SolutionThe following data gives the weights of `30` persons (in kg)
`70.0,69.4,49.4,64.5,59.4,72.4,47.5,48.8,62.3,64.2,66.8,70.3,71.3,56.3,52.7,66.6,59.9,64.7,44.6,60.3,50.3,54.3,62.3,56.3,45.0,45.7,49.8,60.5,67.8,50.1`
(i) Construct a frequency distribution such that the last class is `72-76.`
(ii) State the upper class limits of last three class intervals.
(iii) State the maximum weight that can be included in the fourth class interval.
(iv) State the class mark of each of the classes.
(v) Find the range of the given weights.
(vi) If `60 kg` is the weight of a person then in which class interval, it will be taken.
View SolutionThe approximate speeds of some objects are given below. Draw a bar graph to represent them:
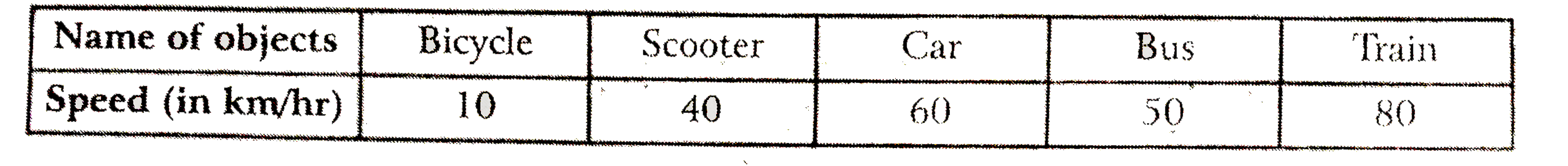
View SolutionGiven below is the data of school going students (boys and girls):
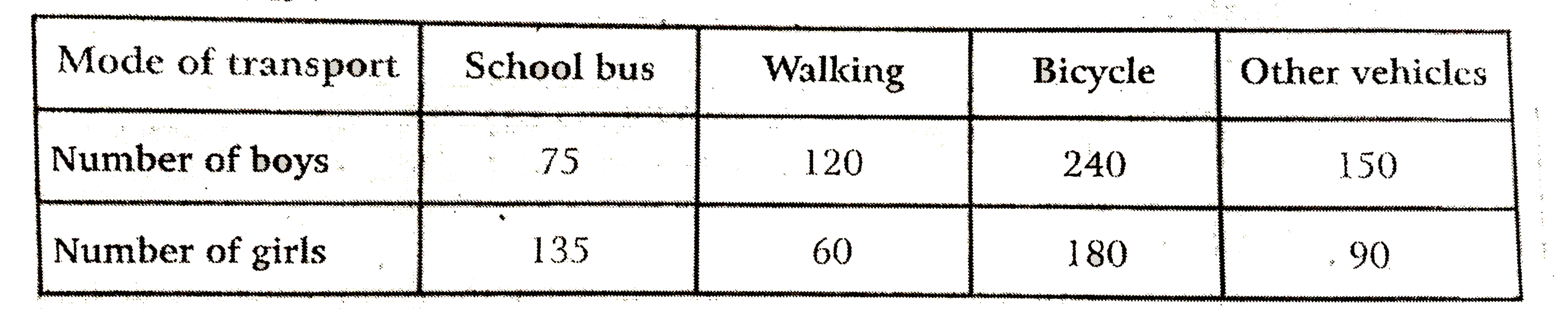
Draw the bar graph to represent the above data.
View SolutionIn a class of 40 students, the marks obtained (out of 50) are as given below:
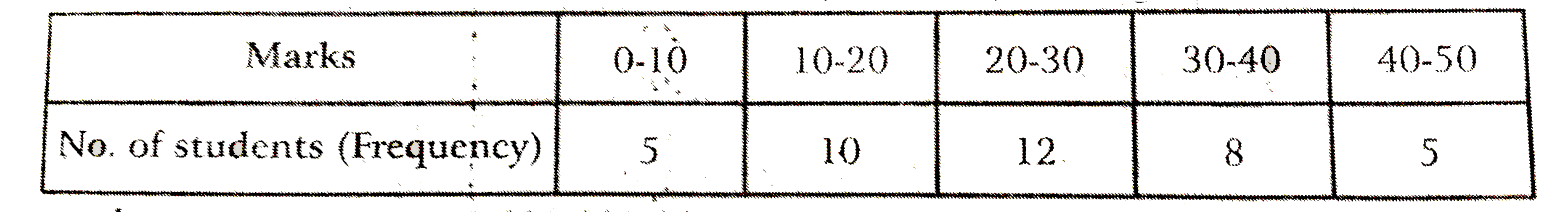
Draw a histogram to represent the given data.
View SolutionDraw a histogram to represent the following:
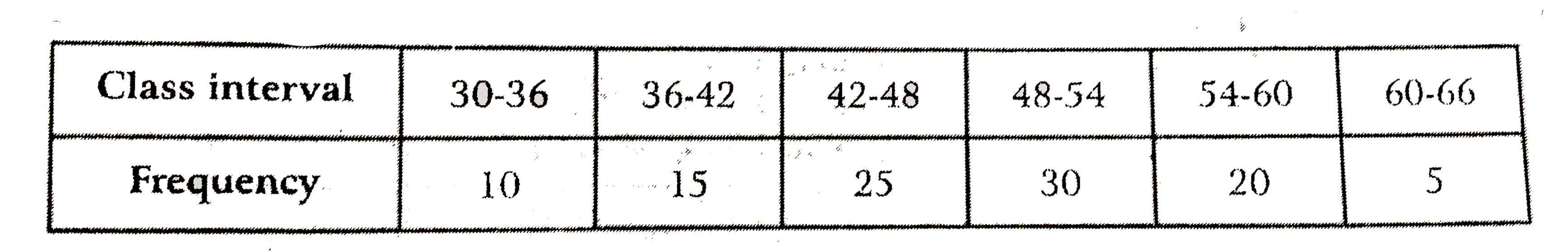
View SolutionDraw a histogram from the following data:
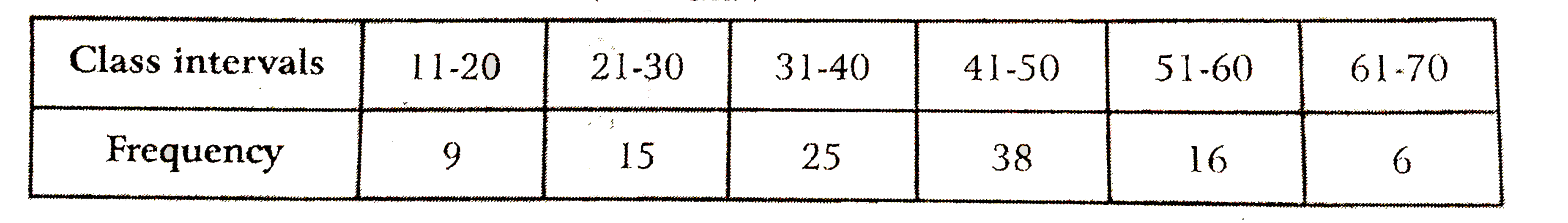
View SolutionDraw a frequency polygon from the following data, giving the age of doctors working in C.G.H.S. in a city.
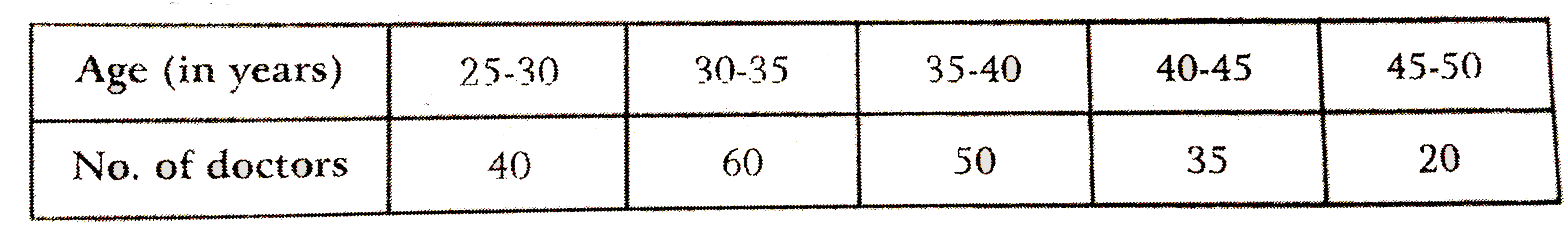
View SolutionThe daily pocket expenses of 206 students in a school are given below.
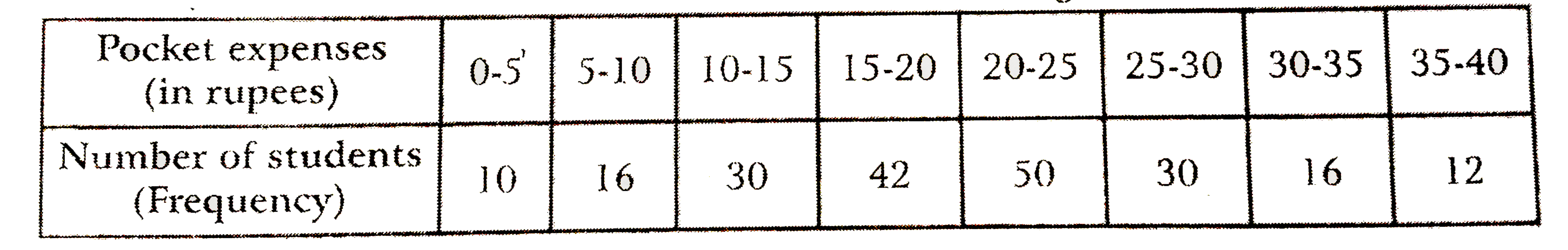
Construct a frequency polygon representing the above data.
View SolutionDraw a histogram for the marks of students given below:

View SolutionFind the mean of 32, 35, 36, 31 and 41.
View SolutionFind the mean of all prime numbers between 20 and 50.
View SolutionThe mean of 10 observations is 12. If mean of first 6 observations is 13. Find the mean of remaining 4 observations.
View SolutionFind the arithmetic mean of:
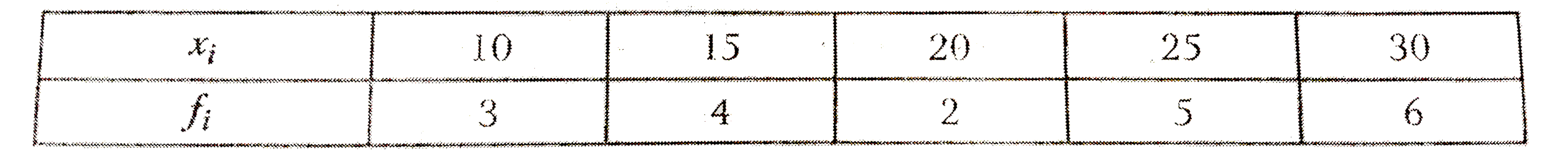
View SolutionThe table shows the marks obtained by 25 students in a class test. Find the mean of the marks obtained
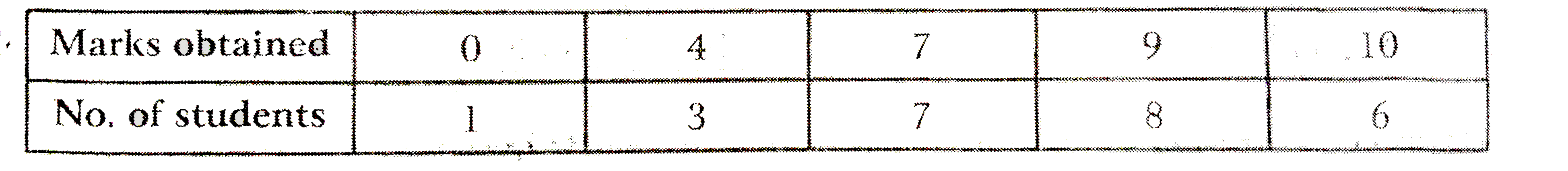
View SolutionFind the median of 7,6,5,3,9,4,3.
View SolutionFind the median of the following data 3,5,9,10,11,4,5,8,12,15
View SolutionFind the mode of 4,6,2,2,1,3,7,9,2,3,2.
View SolutionFind the mode of the following frequency table, which gives the marks scored by 40 students in a test:
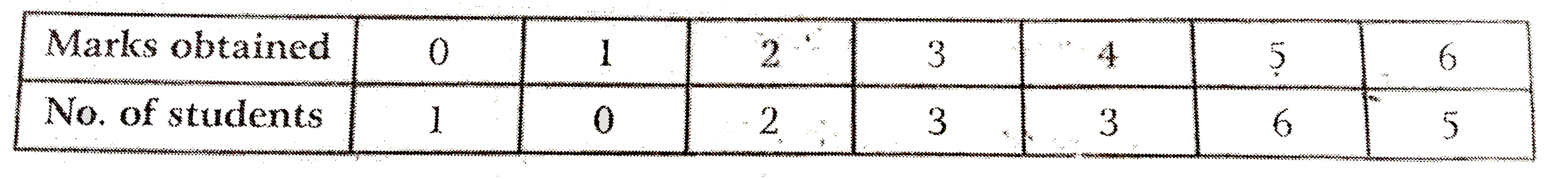
View SolutionIn an examination, the mean of marks scored by a class of 30 students was calculated as 58.5 Later on, it was detected that the marks of one student was wrongly copied as 57 instead of 75. Find the correct mean.
View SolutionFrom a set of `n(n gt 1)` numbers, all except one, which is `n-(1)/(4)` are `n's`. Find the mean of all the `n` numbers.
View SolutionThe average scored by the students of a class in English is `64.` The average of marks scored by boys and the girls are respectively `68` and `58.` Then find the ratio of the number of boys to the number of girls.
View SolutionCalculate the mean of the following distribution :
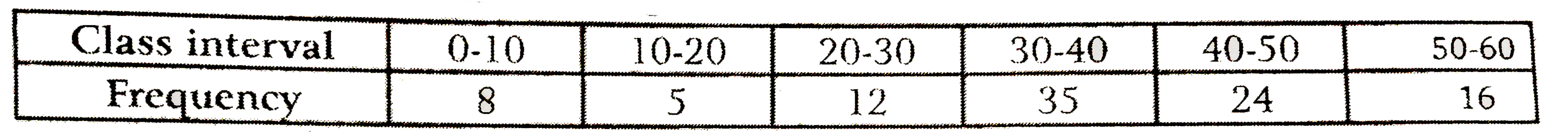
View SolutionFind the value of p, if mean of the following distribution is 7.5.
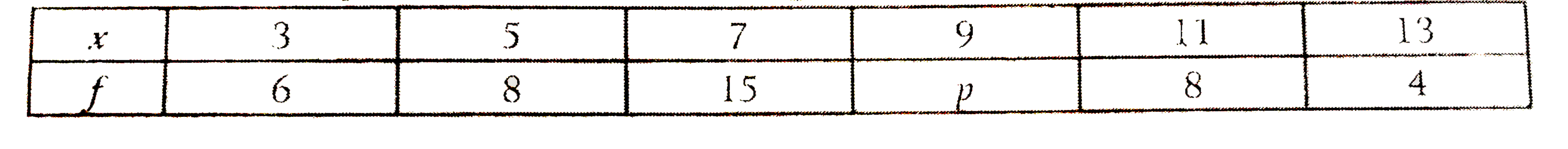
View SolutionThe mean of 1,7,5,3,4 and 4 is m. The numbers 3,2,4,2,3,3 and p have mean m-1. Find m and p.
View SolutionThe sum of deviations of a set of values `x_(1), x_(2), x_(3), …… x_(n)` measured from `50` is `-10` and the sum of deviations of the values from `46` is `70.` Find the value of `n` and the mean.
View SolutionThe following observations have been arranged in ascending order. If the median of the data is 63, find the valueof x.
29,32,48,50,x,x+2,72,78,84,95
View SolutionIf `x_(1), x_(2), ………,x_(n)` are `n` values of a variable `x` such that `sum(x_(i)-3) = 170` and `sum(x_(i)-6) = 50.`
Find the value of `n` and the mean of `n` values.
View Solution
Solved Examples questions and complete solutions for chapter STATISTICS of NAGEEN MATHS (HINGLISH) of Class 9