Complete Solutions to LONG ANSWER TYPE QUESTIONS of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| NCERT EXEMPLAR | LONG ANSWER TYPE QUESTIONS |
| Number Of Questions | 21 |
| Academic Year | 2023-24 |
Find all the angles of an equilateral triangle.
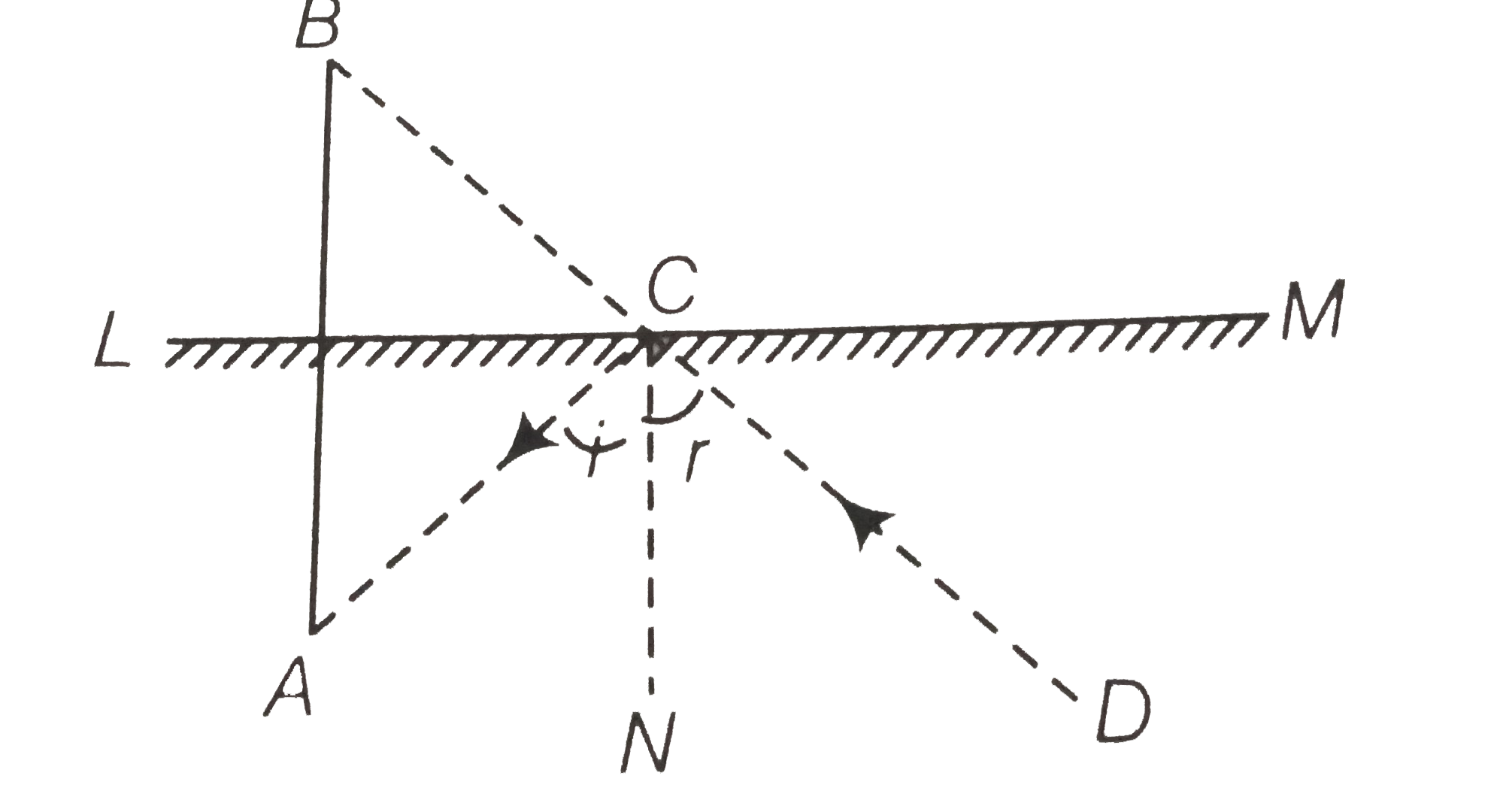
View SolutionThe image of the an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D as shown in figure.prove that the image is as far behind the mirror as the object is in front of the mirror.
View SolutionABC is an isosceles triangle with AB=AC and D is a point on ABC BC such that `AD_|_BC` (see figure ). To prove that `angleBAD =angleCAD ` a student proceeded as follows
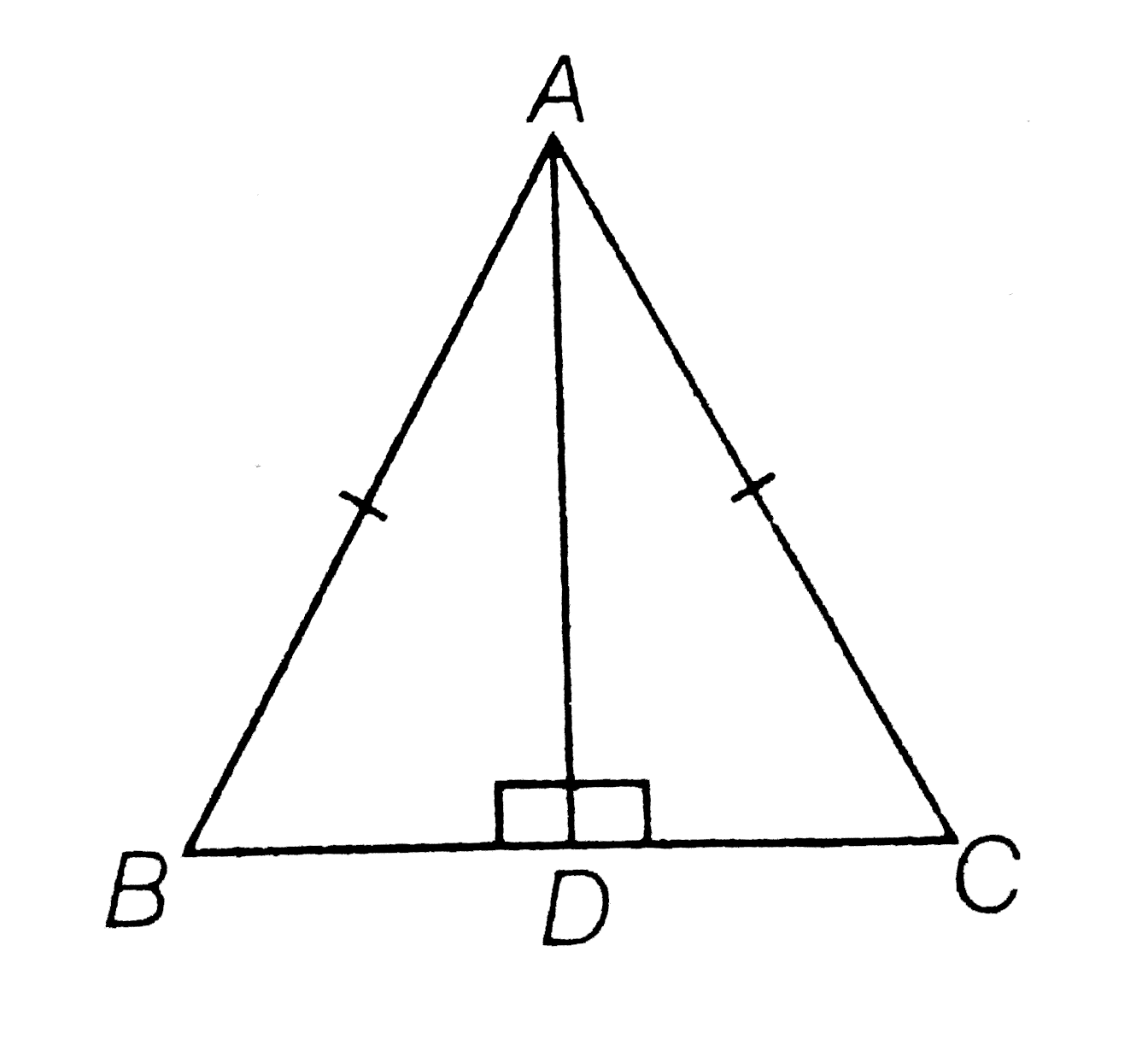
`In Delta ABD and Delta ACD`,we have
` AB=AC " " [" Given"]`
`angleB=angleC " "[because` AB=AC ]
`and " "angleADB= angleADC `
Therefore` " " DeltaABD cong Delta ACD " " ["by AAS congruence rule"]`
So , ` " "angleBAD =angleCAD " " [by CPCT]`
What is the defect in the above argument ?
View Solution`P` is a point on the bisector of `angle ABC ` .If the line through `P`, parallel to `BA` meet at `Q` ,prove that ` Delta BPQ ` is an isosceles triangle.
View Solution`ABCD` is a quadrilateral in which `AB=BC` and `AD =CD` ,Show that `BD` bisects both the `angle ABC` and `angle ADC`.
View Solution`ABC` is a right triangle with `AB` = `AC`.If bisector of `angle A ` meet `BC` at `D` then prove that `BC` =`2` `AD` .
View Solution`O` is a point in the interior of a square `ABCD` such that `Delta OAB ` is an equilateral triangle . Show that `Delta OCD ` is an isosceles triangle .
View SolutionABC and DBC are two triangle on the same base BC such that A and D lie on the opposite sides of BC,AB=AC and DB =DC ,Show that AD is the perpedicular bisector of BC.
View SolutionIn Figure, ` A D\ a n d\ B E` are respectively altitudes of an isosceles triangle `A B C` with `A C=B Cdot` Prove that `A E=B D`
View SolutionProve that sum of any two sides of a triangle is greater than twice the median with respect to the third side.
View SolutionShow that in a quadrilateral ABCD `AB+BC+CD+DA lt 2 (BD + AC)`
View SolutionShow that in a quadrilateral ABCD `AB+BC+CD+DA gt AC + BD`
View SolutionIn a `Delta ABC ,` `D` is the mid point of side `AC` such that `BD` `=1/2` `AC`. Show that `angleABC` is a right angle.
View SolutionIn a right triangle,Prove that the line-segment joining the mid-point of the hypotenuse to the opposite vertex is half the hypotenuse
View SolutionTwo lines l and m interset at the O and P is Point on a line n Passing through the point O such that P is equidistant from l and m. Prove that n is the bisectof the angle formed by l and m
View SolutionThe line segments joining the midpoints `M` and `N` of parallel sides `AB` and `DC` respectively of a trapezium `ABCD` is perpendicular to both the sides `AB` and `DC`. Prove that `AD`=`BC`.
View SolutionIn Figure, diagonal `A C` of a quadrilateral `A B C D` bisects the angles `A` and `C` . Prove that `A B=A D` and `C B=CD`.
View Solution`DeltaABC` is a right triangle right angled at A such that `AB = AC` and bisector of `/_C` intersects the side `AB` at `D`. Prove that `AC + AD = BC`.
View SolutionIn Figure, `A B\ a n d\ C D` are respectively the smallest and longest sides of a quadrilateral `A B C Ddot` Show that `/_A >/_C\ a n d\ /_B >/_D`
View SolutionProve that in a triangle, other than an equilateral triangle, angle opposite the longest side is greater than `2/3` of a right angle.
View SolutionIf `ABCD` is a quadrilateral such that `AB` `=` `AD` and `CB` `=` `CD` , then prove that `AC` is the perpendicular bisector of `BD`.
View Solution
LONG ANSWER TYPE QUESTIONS questions and complete solutions for chapter TRIANGLES of NCERT MATHS (ENGLISH) of Class 9