In Figure, AD and BE are respectively altitudes of an isosceles triangle ABC with AC=BC. Prove that AE=BD
Given ΔABC is an isosceles triangle in which AC=BC,AD and BE are respectively two altitude to sides BC and AC respectively
To Prove AE=BD
Proof in ΔABC AC=BC [given ]
∠ABC=∠CAB
[angles opposite to equal sides are equal ]
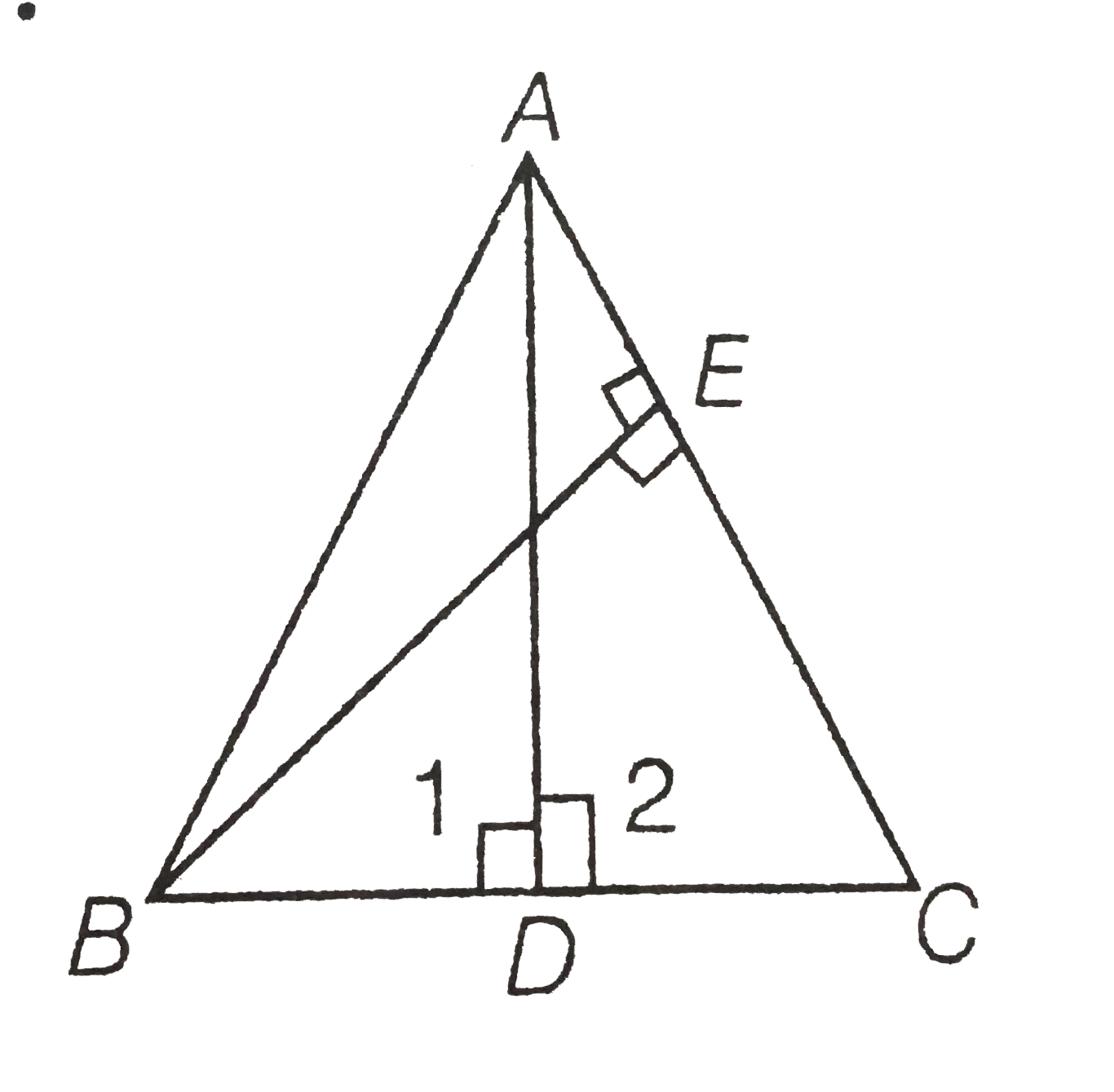
∠ABD=∠EAB
in ΔAEBandΔBDA,
∠AEB=∠ADB=90∘[ given ,AD⊥BC and BE⊥AC]
∠EAB=∠ABD [ from E q,(i) ]
and AB=AB [common side ]
∴ΔAEB≅ΔBDA [by AAS congruence rule ]
⇒ AE=BD [by CPCT ]
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - SHORT ANSWER TYPE QUESTIONS11videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS12videos
STATISTICS AND PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - VOLUME AND SURFACE AREAEXERCISE - LONG ANSWER TYPE QUESTIONS8videos
VOLUME AND SURFACE AREA
Similar Questions
AD and BE are respectively altitudes of an isosceles triangle ABC with AC=BC . Prove that AE=BD.
View SolutionAD and BE are respectively altitudes of ABC such that AE=BD. Prove that AD=BE.
View SolutionIn an isosceles triangle ABC with AB=AC and BD⊥AC. Prove that BD2−CD2=2CD.AD.
View SolutionBD and CE are bisectors of ∠B and ∠C of an isosceles ABC with AB=AC. Prove that BD=CE.
View SolutionBD and CE are bisectors of ∠B and ∠C of an isosceles ABC with AB=AC . Prove that BD=CE
View SolutionIn Figure, D,E and F are, respectively the mid-points of sides BC,CA and AB of an equilateral triangle ABC . Prove that DEF is also an equilateral triangle.
View SolutionIn Figure, D,E and F are, respectively the mid-points of sides BC,CA and AB of an equilateral triangle ABC . Prove that DEF is also an equilateral triangle.
View SolutionD and E are, respectively, the points on equal sides AB and AC of an isosceles triangle ABC such that B, C, E, and D are concyclic as shown in Figure. If O is the point of intersection of CD and BE, prove that AO is the bisector of line segment DE
View SolutionIn Figure, AB=AC.BE and CF are respectively the bisectors of ∠B and ∠C . Prove that ECB ≅ FCB
View SolutionIn figureE is a point on side CB produced of an isosceles △ABC with AB=AC. If AD⊥BCandEF⊥AC, prove thatΔABD~ΔECF.
 View Solution
View Solution

