Complete Solutions to Exercise-9.4 Long Answer Type Questions of chapter Areas of Parallelograms and Triangles of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | Areas of Parallelograms and Triangles |
| NCERT EXEMPLAR | Exercise-9.4 Long Answer Type Questions |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
A point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that `ar(DeltaADF) = ar (ABFC)`.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line a drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
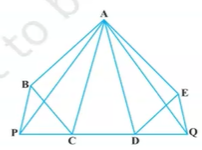
View SolutionThe median BE and CF of a triangle ABC intersect at G. Prove that the area of `DeltaGBC =` area of the quadrilateral AFGE.
View SolutionIn figure, `CD || AE` and `CY || BA`. Prove that `ar (DeltaCBX) = ar (DeltaAXY)`.

View SolutionABCD is trapezium in which `AB||DC`, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that
`ar (DCYX) = (7)/(9) ar (XYBA)`.
View SolutionIn `DeltaABC` , if L and M are the points on AB and AC, respectively such that `LM || BC`. Prove that `ar (DeltaLOB) = ar (DeltaMOC)`.
View SolutionIn figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that `ar (ABCDE) = ar (DeltaAPQ)`.
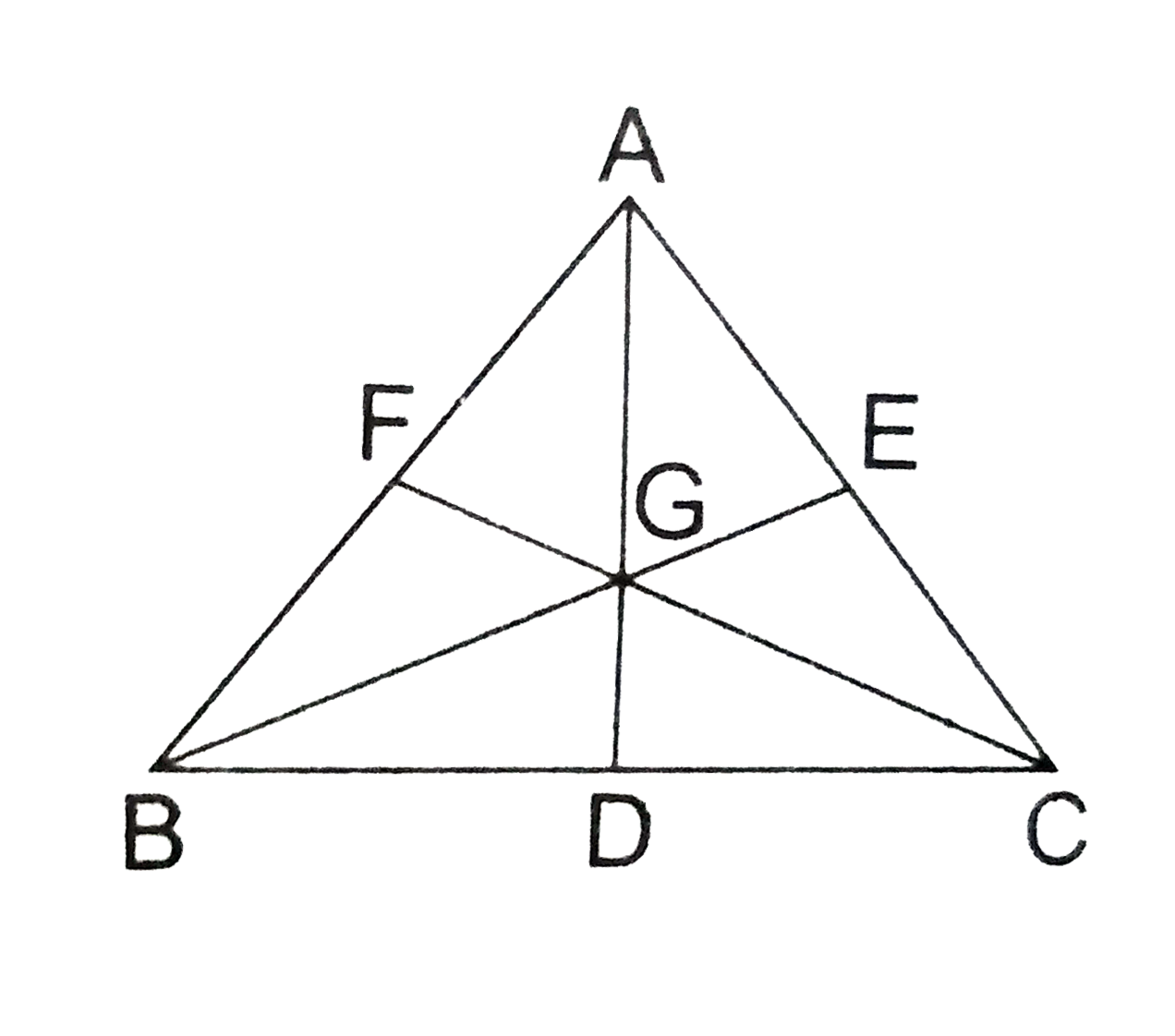
View SolutionIf the medians of a `triangle`ABC intersect at G, show that
`ar(triangleAGB)=ar(triangleAGC)=ar(triangleBGC)`
`=(1)/(3)ar(triangleABC)`.
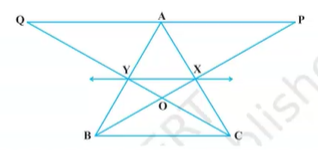
View SolutionIn figure X and Y are the mid-points of AC and AB respectively, `QP || BC` and CYQ and BXP are straight lines. Prove that `ar (DeltaABP) = ar (DeltaACQ)`.
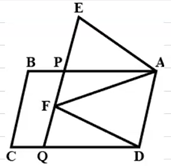
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that `ar (DeltaPEA) = ar (DeltaQFD)`.
View Solution
Exercise-9.4 Long Answer Type Questions questions and complete solutions for chapter Areas of Parallelograms and Triangles of NCERT MATHS (ENGLISH) of Class 9