Complete Solutions to साधित उदाहरण of chapter वृत्त of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | वृत्त |
| MADHUR GUPTA | साधित उदाहरण |
| Number Of Questions | 52 |
| Academic Year | 2023-24 |
संलग्न चित्र में `O` वृत्त का केन्द्र है | यदि व्यास `AC = 26` सेमी और जीवा `AB = 10 ` सेमी है, तो वृत्त के केन्द्र से `AB` पर लम्ब की लम्बाई ज्ञात कीजिए |
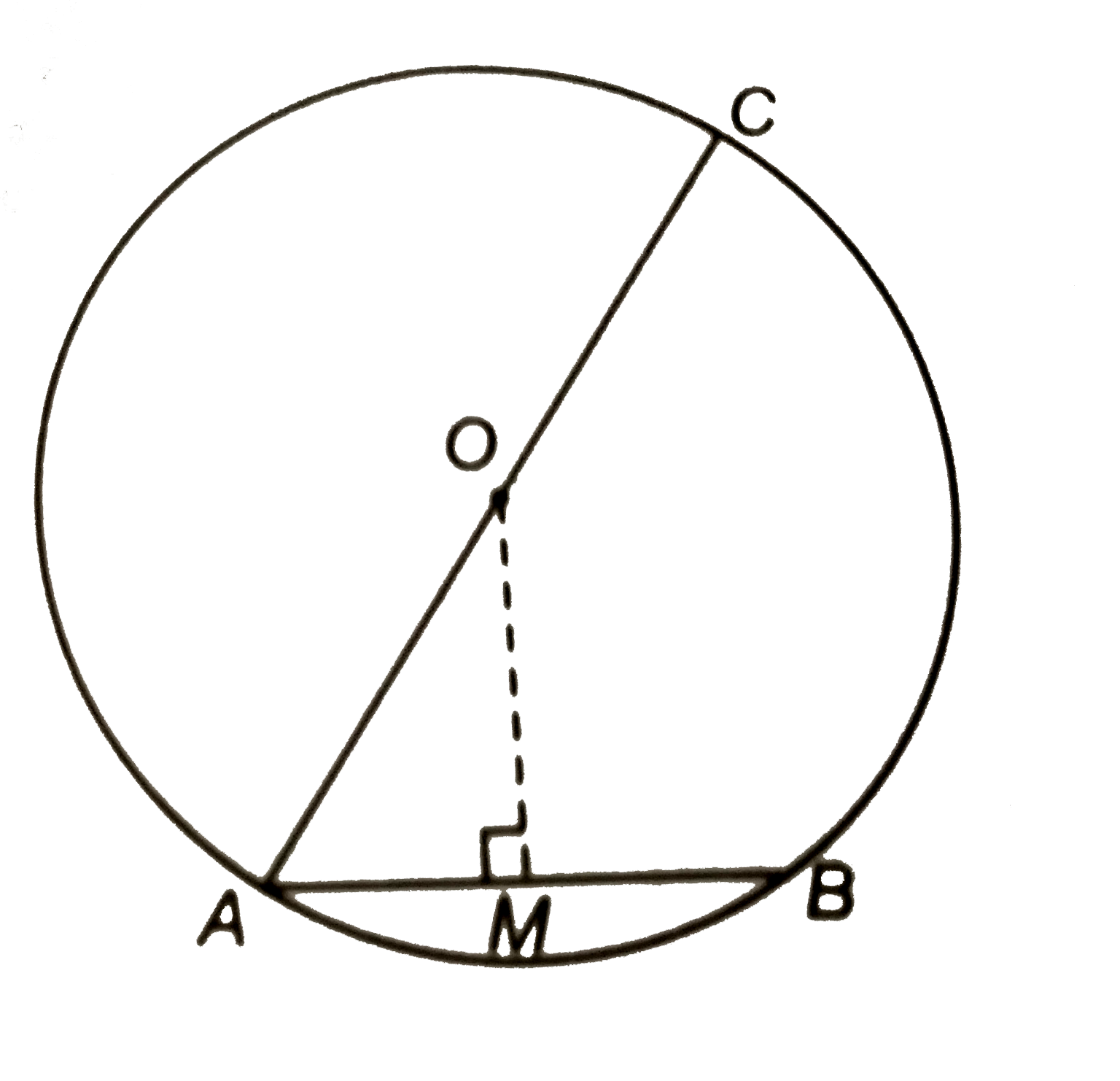
View Solutionएक वृत्त की 16 सेमी लम्बी जीवा वृत्त के केन्द्र से 6 सेमी की दुरी पर है | वृत्त का व्यास ज्ञात कीजिए |
View Solutionसंलग्न चित्र में BD वृत्त का व्यास है जो जीवा AC को E बिन्दु पर समद्विभाजित करता है | यदि AC = 8 सेमी, BE = 2 सेमी, तो वृत्त की त्रिज्या ज्ञात कीजिए |

View Solutionसंलग्न चित्र में A और B दो व्रतों के केन्द्र हैं | यदि CB = 17 सेमी, EB = 15 सेमी, तो दोनों वृत्तों की उभयनिष्ठ जीवा की लम्बाई ज्ञात कीजिए |
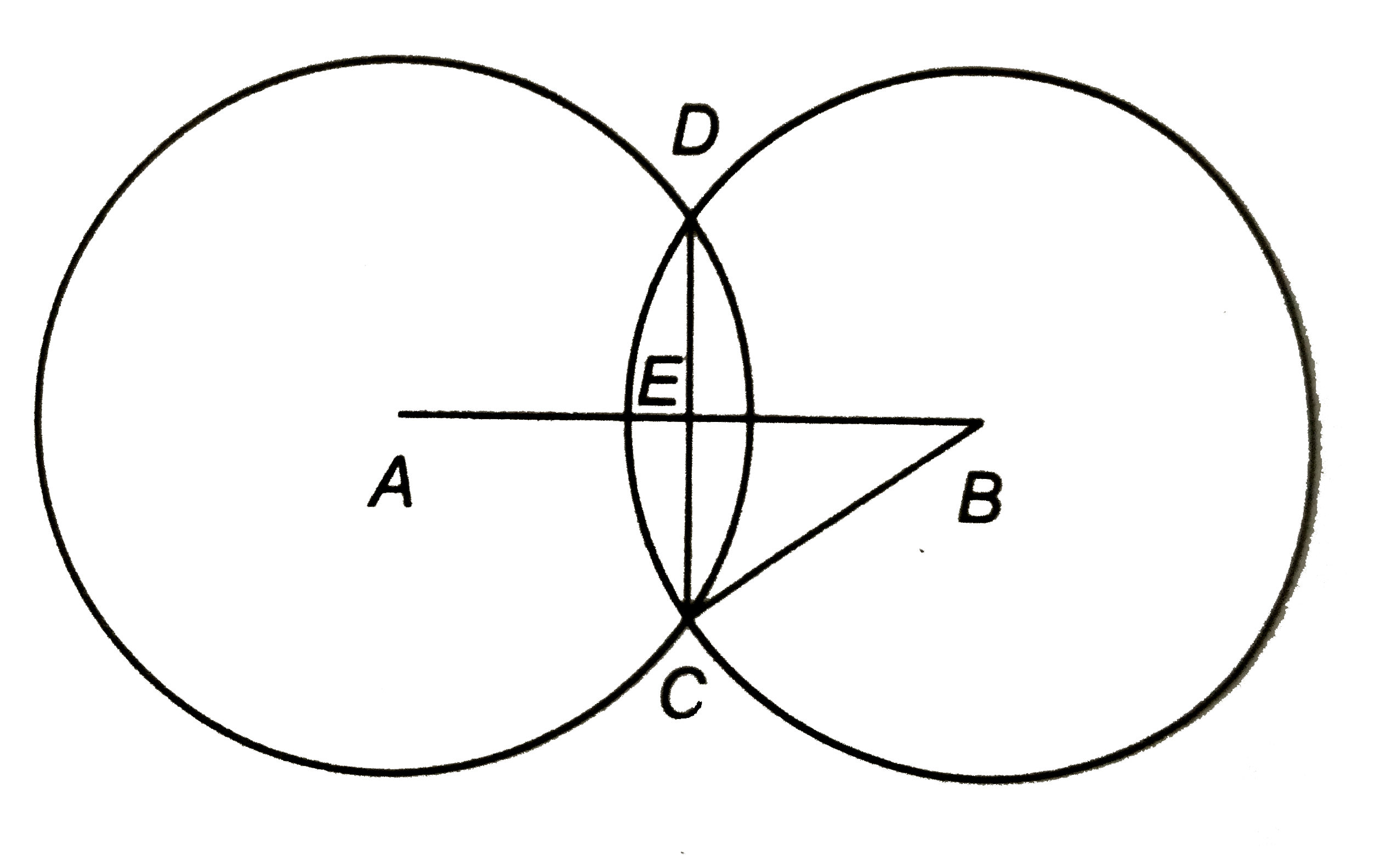
View Solutionयदि वृत्त की दो जीवाओं के मध्य बिन्दुओं को मिलाने वाली रेखा वृत्त के केन्द्र से होकर जाती है, तो दिखाइए की दोनों जीवाएँ समान्तर होंगी |
View Solutionसिद्ध कीजिए की एक वृत्त की दो समान्तर जीवाओं के मध्य बिन्दुओं को मिलाने वाला रेखाखण्ड वृत्त के केन्द्र से होकर जाता है |
View Solutionएक समबाहु त्रिभुज में, सिद्ध कीजिए कि केन्द्रक और परिवृत्त का केन्द्र (परिकेन्द्र) सम्पाती होते हैं |
View Solutionचित्र में, `overset(frown)("AB")~=overset(frown)(AC)` और O वृत्त का केन्द्र है | सिद्ध कीजिए की OA, BC का लम्ब समद्विभाजक है |
View Solutionएक वृत्त के केन्द्र के दोनों ओर दो समान्तर जीवाएँ AB और CD हैं | यदि AB = 10 सेमी, CD = 24 सेमी और इनके बीच की दूरी 17 सेमी है, तो वृत्त की त्रिज्या ज्ञात कीजिए |
View SolutionO' केन्द्र के वृत्त के बाहर एक बिन्दु P स्थित है | P से वृत्त पर दो रेखाएँ PAOB और PDC खींची गयी हैं | यदि PD = DO, तो सिद्ध कीजिए कि चाप `BC=3xx" चाप "AD`.
View Solutionसिद्ध कीजिए कि वृत्त के किसी व्यास या त्रिज्या के साथ समान कोण बनाने वाली जीवाएँ बराबर होती हैं |
View Solutionचित्र में, वृत्त कि एक जीवा AB पर लम्ब OD है जहाँ O वृत्त का केन्द्र है | यदि BC एक व्यास है, तो सिद्ध कीजिए कि `CA=2OD`.
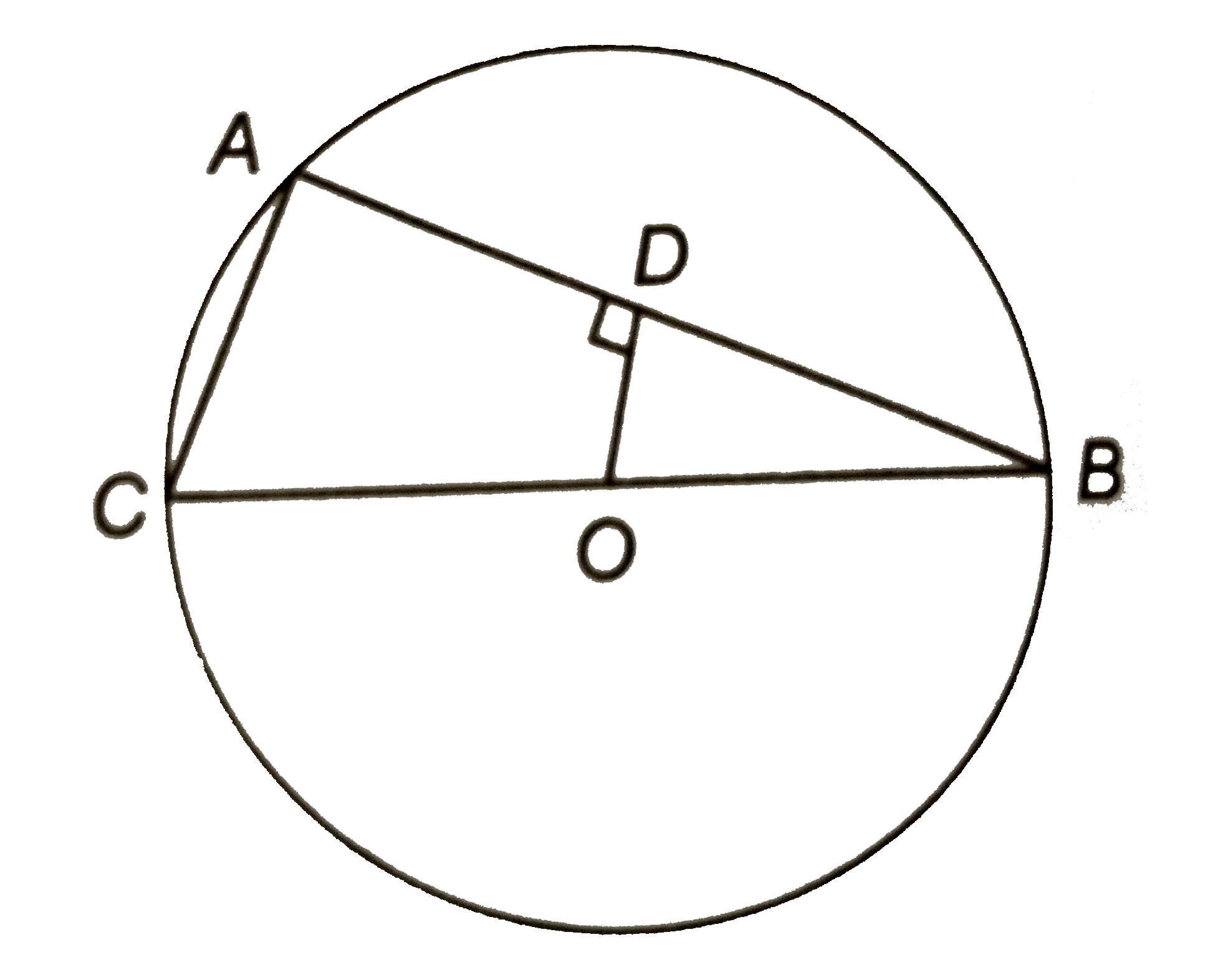
View SolutionAB और CD एक वृत्त की दो समान्तर जीवायें हैं जिसका व्यास AC है | सिद्ध कीजिए कि AB = CD.
View Solutionदो वृत्त जिनके केन्द्र O और O' हैं, बिन्दु P पर प्रतिच्छेद करते हैं | P से होकर एक रेखा l, OO' के समान्तर खींचते हैं जो दोनों वृत्तों को क्रमश: C और D पर काटती है | सिद्ध कीजिए कि `"CD"=2" OO'"`.
View Solutionसिद्ध कीजिए कि एक वृत्त की दो बराबर जीवाओं के मध्य बिन्दुओं को मिलाने वाली रेखा जीवा के साथ बराबर कोण बनाती है |
View Solutionसंलग्न चित्र में, यदि एक वृत्त की दो बराबर जीवायें AB और CD एक दूसरे को E पर काटती हैं, तो सिद्ध कीजिए कि जीवायें AC और DB बराबर हैं |

View SolutionO केन्द्र के वृत्त की एक जीवा AB है | AB को C तक इस प्रकार बढ़ाया गया है कि BC = OB है | CO को मिलाकर बढ़ाया गया है जो वृत्त पर D पर मिलती हैं |
यदि `angleACD=y^(@)"और "angleAOD=x^(@)` तो सिद्ध कीजिए `x=3y`.
View Solutionसंलग्न चित्र में, A और B केन्द्र और 5 सेमी और 3 सेमी त्रिज्या के दो वृत्त एक-दूसरे को अन्त:स्पर्श करते हैं | यदि रेखाखण्ड AB का लम्ब समद्विभाजक बड़े वृत्त को P और Q पर मिले तो PQ की लम्बाई ज्ञात कीजिए |
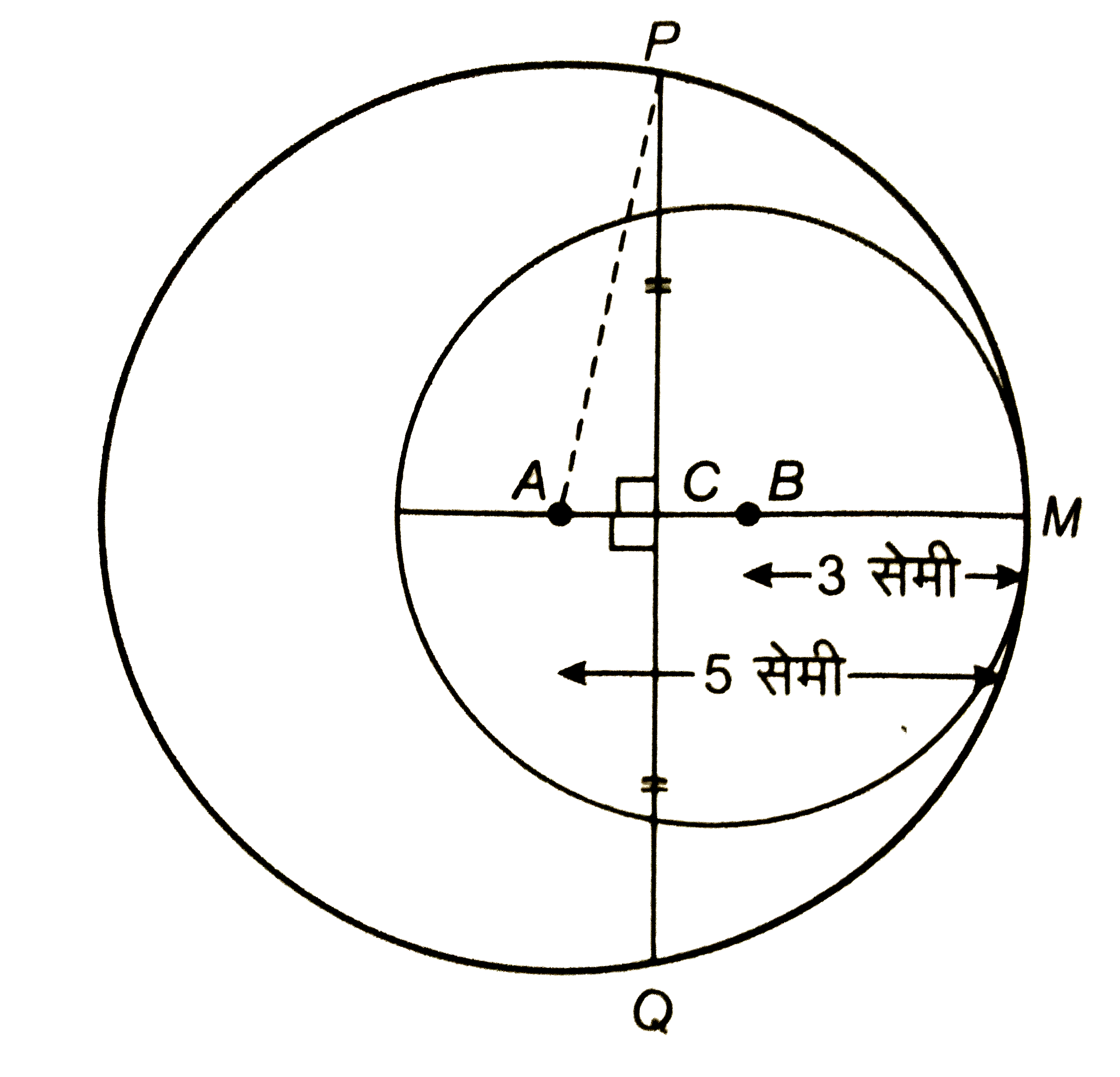
View SolutionO एक वृत्त की दो जीवाओं में दिखाइए कि एक जीवा जो बड़ी है, केन्द्र के पास होती हैं | (बड़ी जावी केन्द्र के ज्यादा समीप होती है) |
View Solutionसंलग्न चित्र में, `angleQPO=25^(@)` और `angleSPR=20^(@),angleQOR` का मान ज्ञात कीजिए |

View Solutionसंलग्न चित्र में, 'O' वृत्त का केन्द्र है | यदि जीवा AB = 2 सेमी और वृत्त की त्रिज्या OA = 2 सेमी है तो `angleACB` का मान ज्ञात कीजिए |
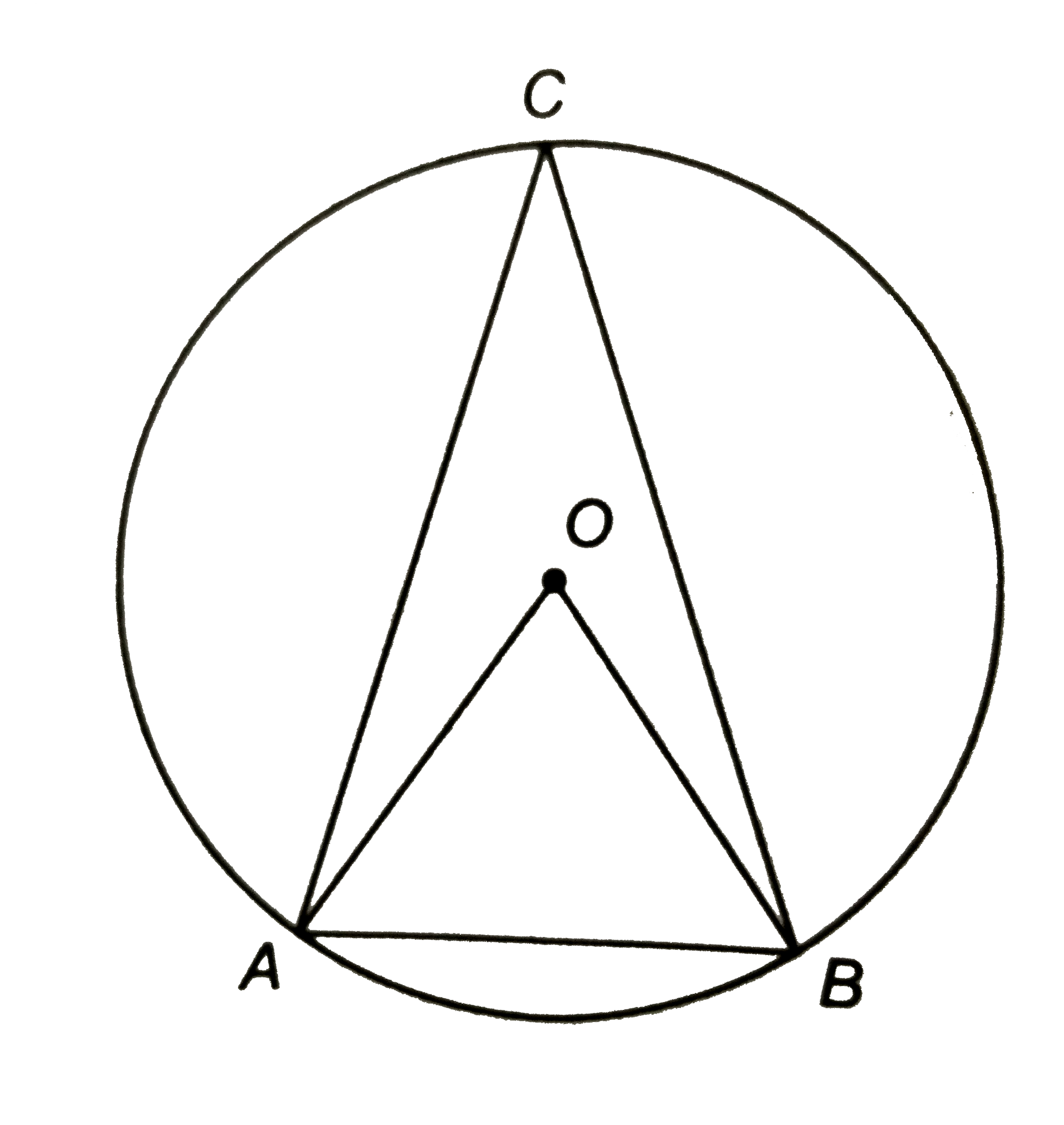
View Solutionसंलग्न चित्र में, 'O' वृत्त का केन्द्र है और `angleOAB=60^(@)` है | `angleAPC` ज्ञात कीजिए |

View Solutionसंलग्न चित्र में 'O' वृत्त का केन्द्र है तथा ACB एक वृत्तखण्ड है | यदि `angleOAB=30^(@)`, तो `angleACB` ज्ञात कीजिए |

View Solutionसंलग्न चित्र में, 'O' वृत्त का केन्द्र है यदि `angleACB=60^(@)` और `DA=DB`, तो सिद्ध कीजिए कि `DeltaADB` एक समबाहु त्रिभुज है |
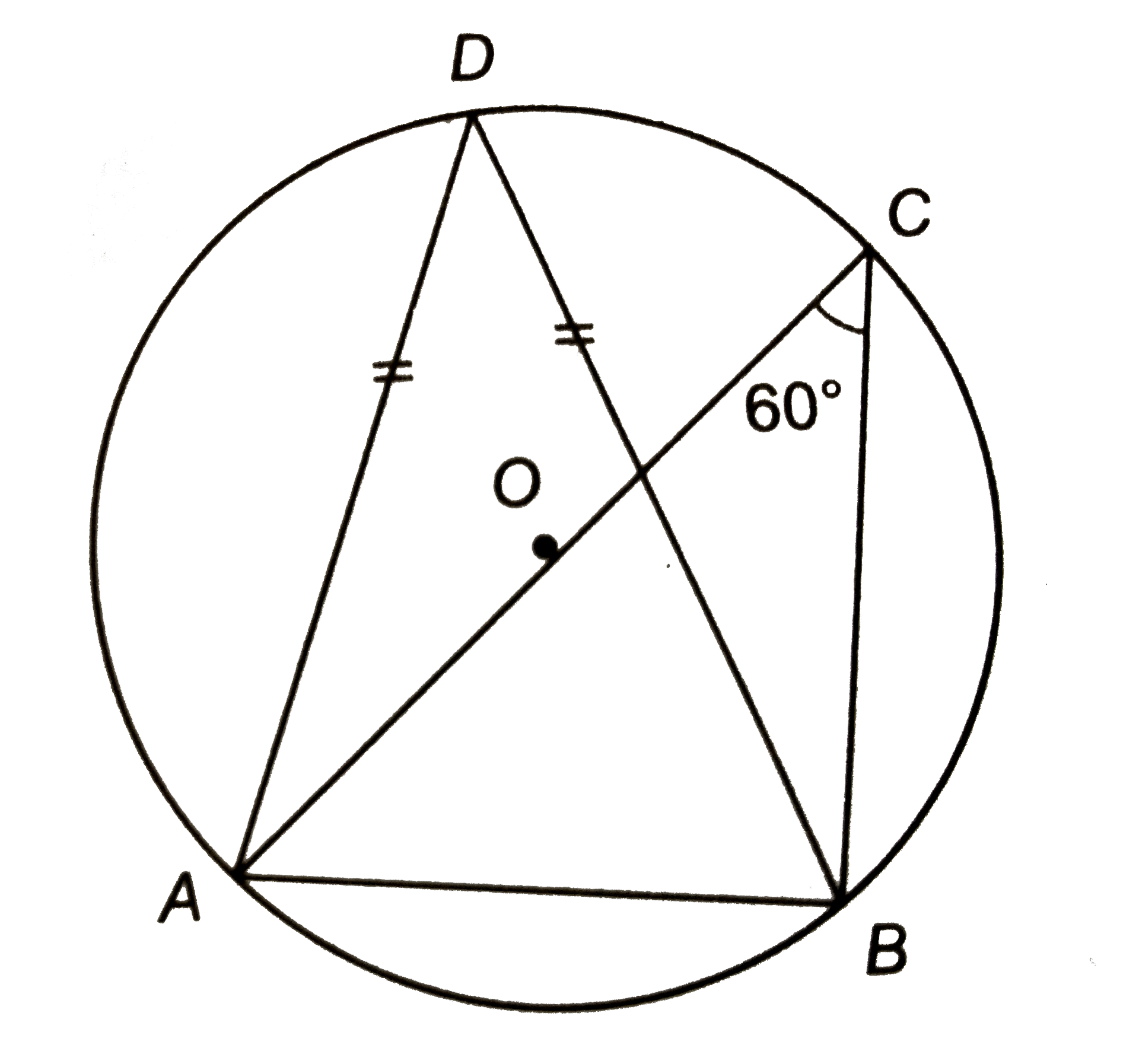
View Solutionसंलग्न चित्र में BP वृत्त का व्यास है | यदि `angleABP=60^(@)`, तो `angleAQB` ज्ञात कीजिए |
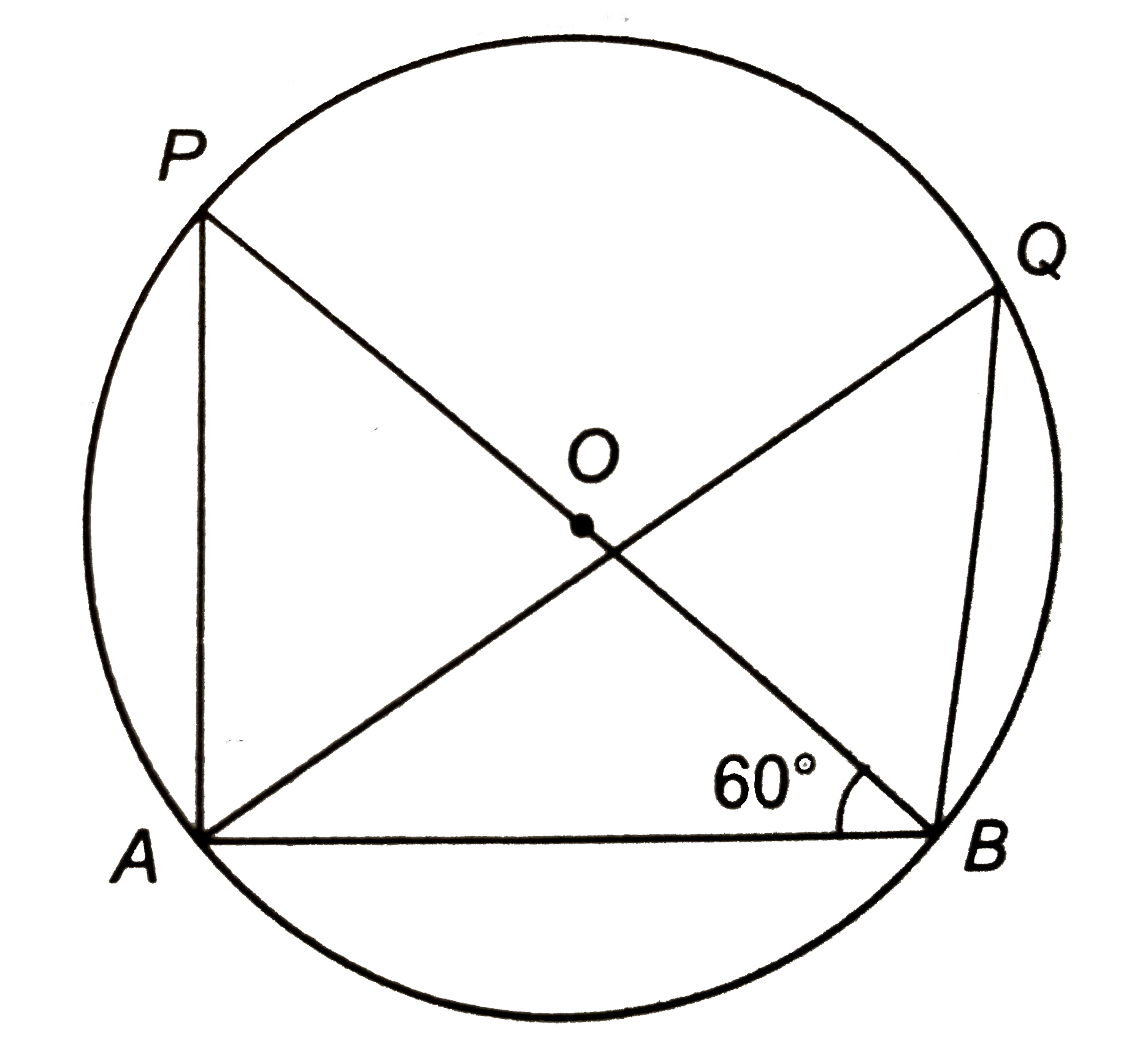
View Solutionसंलग्न चित्र में दो वृत्त एक-दूसरे को A और B पर काट रहे हैं | वृत्तों के व्यास AP और AQ हैं | सिद्ध कीजिए कि PBQ एक सरल रेखा है |

View Solutionदी आकृति में, ABC एक त्रिभुज है तथा भुजा BC पर एक बिन्दु P इस प्रकार है की AB = AP है | यदि बढ़ाई गई AP, `DeltaABC` के परिवृत्त को Q पर मिलती है तो सिद्ध कीजिए कि CP = CQ.
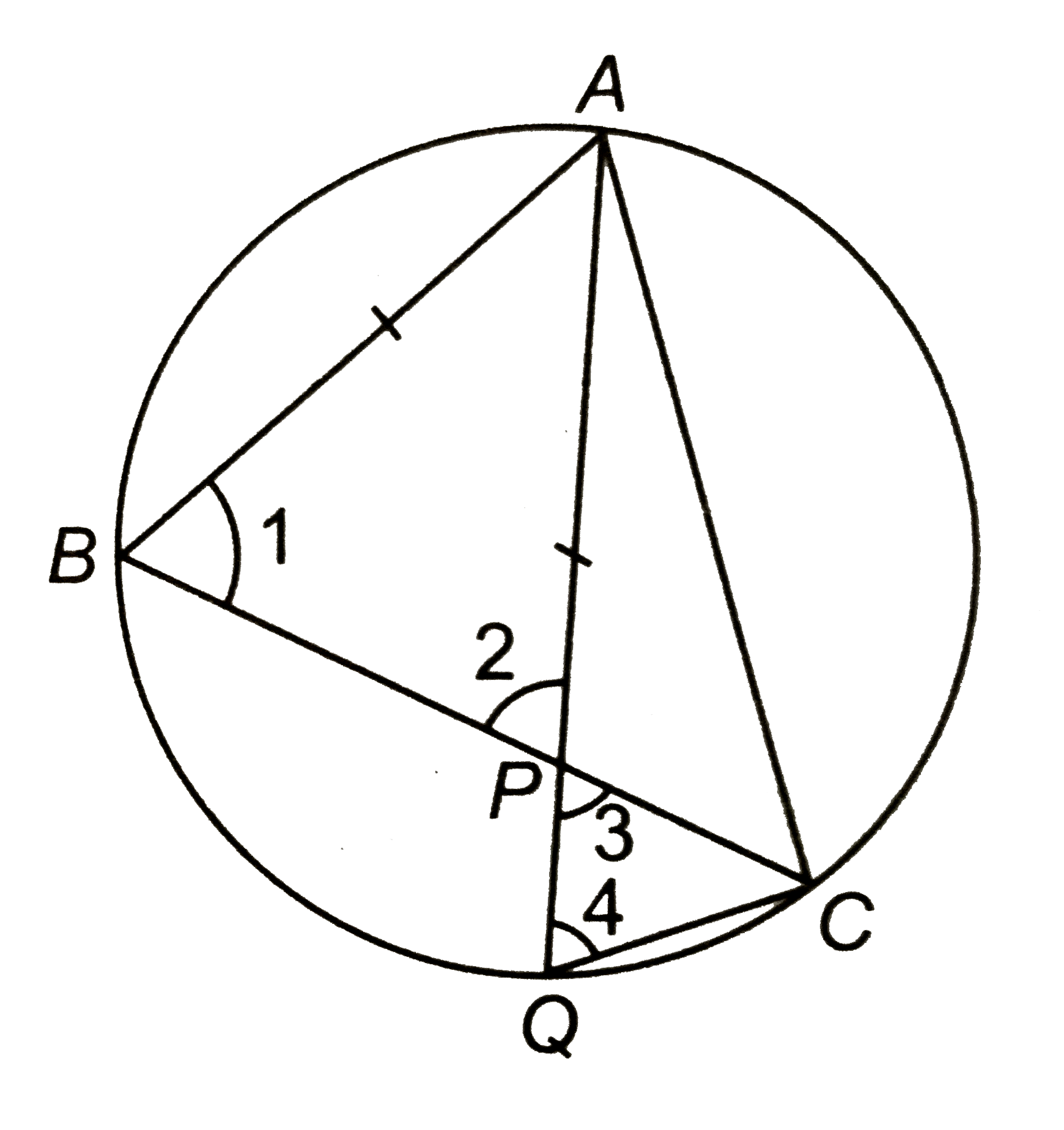
View Solution`DeltaABC` जिसमें `AB=AC` है, के परिवृत्त पर एक बिन्दु D इस प्रकार है कि B और D रेखा AC के विपरीत और स्थित हैं | यदि CD को E तक इस प्रकार बढ़ाया गया है कि CE = BD तो सिद्ध कीजिए कि AD = AE है |
View Solutionसंलग्न चित्र में, P वृत्त का केन्द्र है | सिद्ध कीजिए कि `angleXPZ=2(angleXZY+angleYXZ)`

View Solutionसिद्ध कीजिए कि किसी समद्विबाहु त्रिभुज कि बराबर भुजाओं में से किसी एक भुजा को व्यास लेकर खिंचा गया वृत्त, आधार को समद्विभाजित करता है |
View SolutionO केन्द्र के वृत्त में, जीवायें AB और CD परिधि के अन्दर बिन्दु E पर कटती हैं | सिद्ध कीजिए कि `angleAOC+angleBOD=2angleAEC`.
View Solutionसंलग्न चित्र में, O वृत्त का केन्द्र है | सिद्ध कीजिए कि `angle z=angle x+angle y`. ltbr.

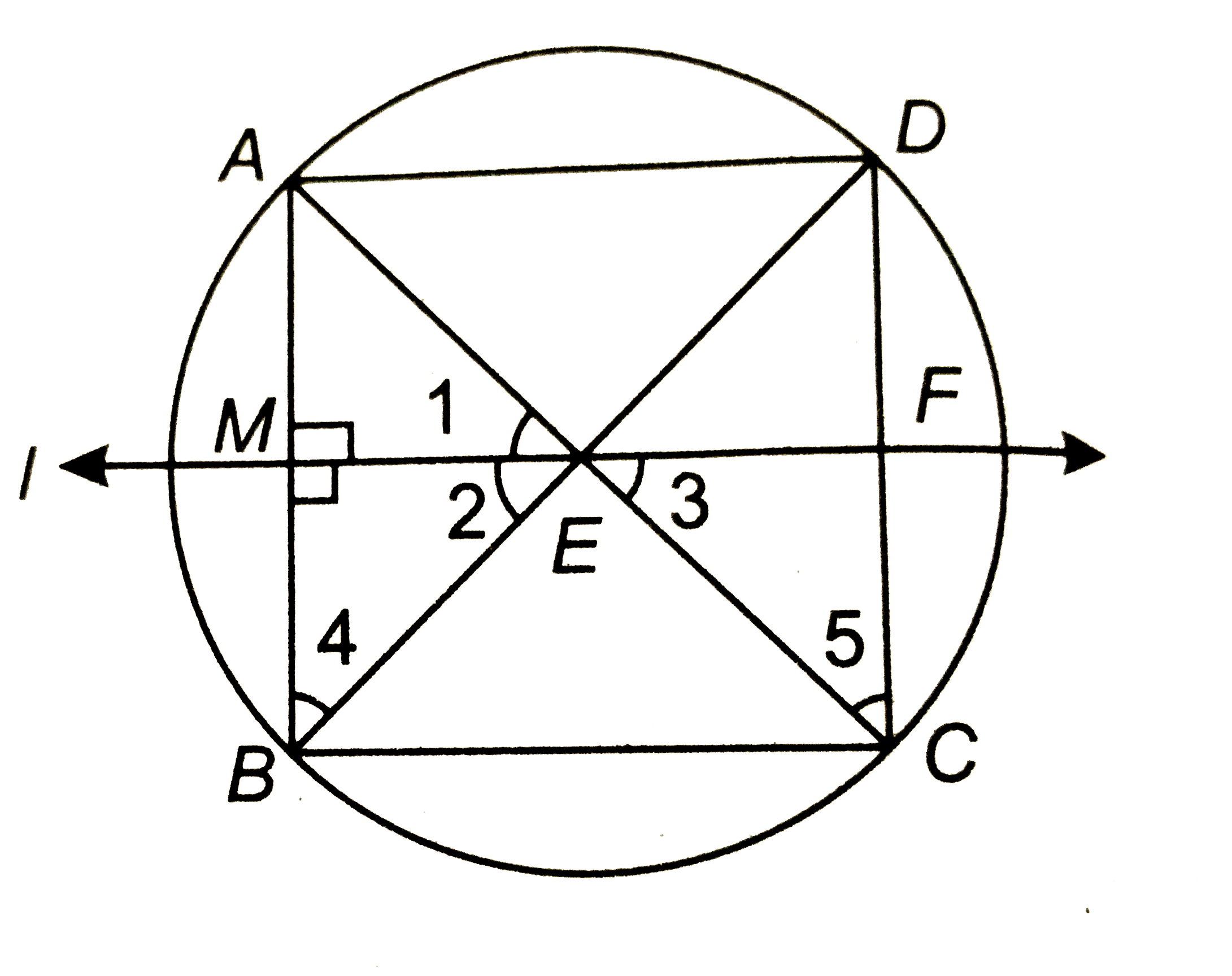
View Solutionचक्रीय चतुर्भुज ABCD के विकर्ण AC और BD एक दूसरे को E पर समकोण पर प्रतिच्छेद करते हैं (चित्र देखें) | E से होकर जाने वाली तथा AB के लम्बवत रेखा l, CD को F पर मिलती है | सिद्ध कीजिए कि F, CD का मध्य बिन्दु है |
View SolutionO केन्द्र के वृत्त का व्यास AB है और जीवा CD त्रिज्या OC के बराबर है (चित्र देखें) | बढ़ाई गई AC और BD एक-दूसरे को P पर मिलती है | सिद्ध कीजिए कि `angleCPD=60^(@)` है |

View Solutionदिये चित्र में, यदि `(x)/(3)=(y)/(4)=(z)/(5)`, तो x,y और z के मान ज्ञात कीजिए |
View Solutionसिद्ध कीजिए कि एक समपंचभुज के कोई चार शीर्ष चक्रीय होते हैं |
View Solutionसंलग्न चित्र में 'O' वृत्त का केन्द्र है | A वृत्त के बाहर एक बिन्दु है | चित्र में कोण x, y ओर z दर्शायें गये हैं | दिखाइए कि :
`x+y=z.`
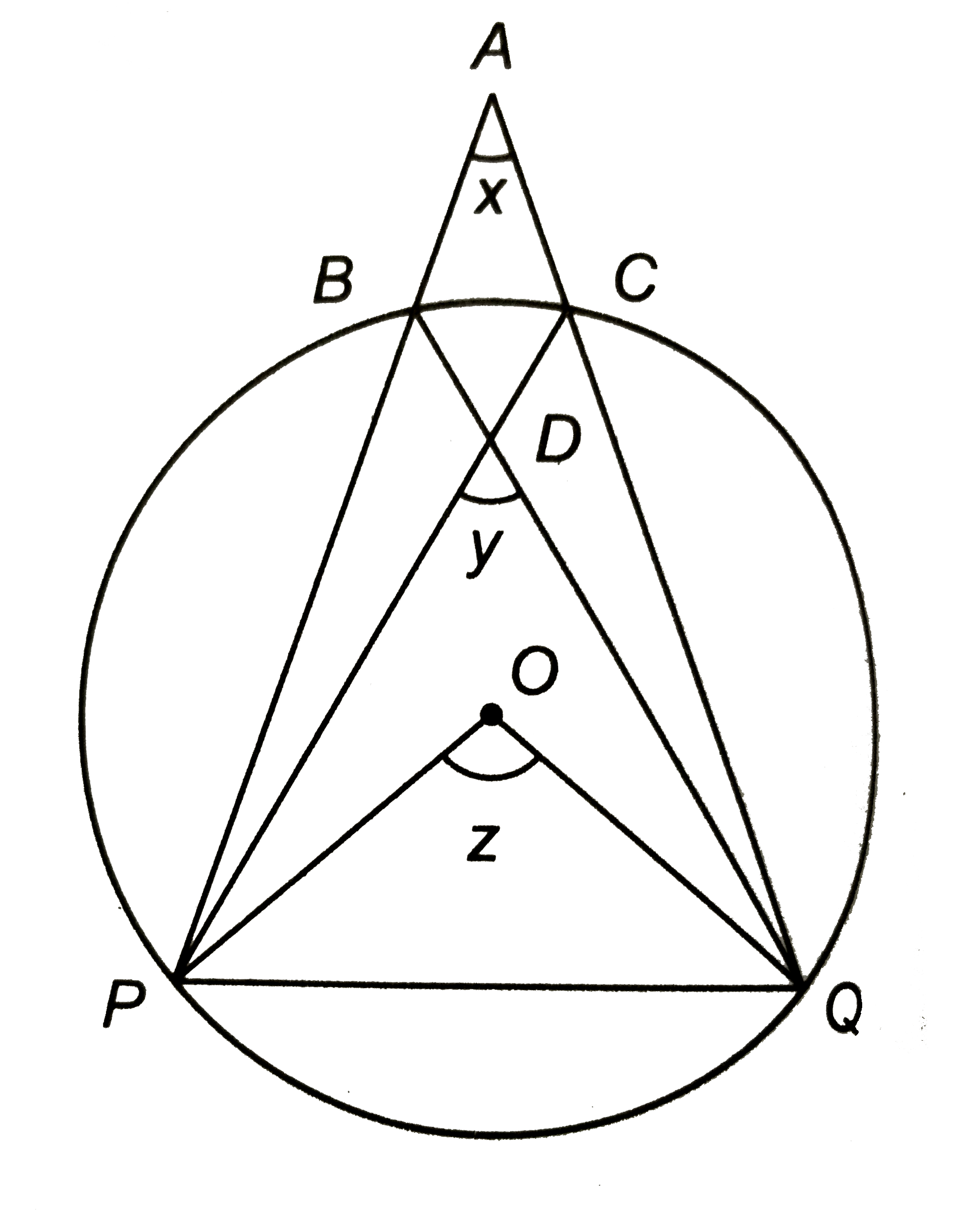
View Solutionएक वृत्त की दो जीवायें PQ ओर QR केन्द्र 'O' से समदूरस्थ हैं | यदि QS व्यास है, तो सिद्ध कीजिए कि QS, `anglePQR` और `anglePSR` दोनों को समद्विभाजित करती है |
View Solutionसंलग्न चित्र में, 'O' वृत्त को केन्द्र तथा `angleAOB=100^(@)` है | `angleBCD` का मान ज्ञात कीजिए |
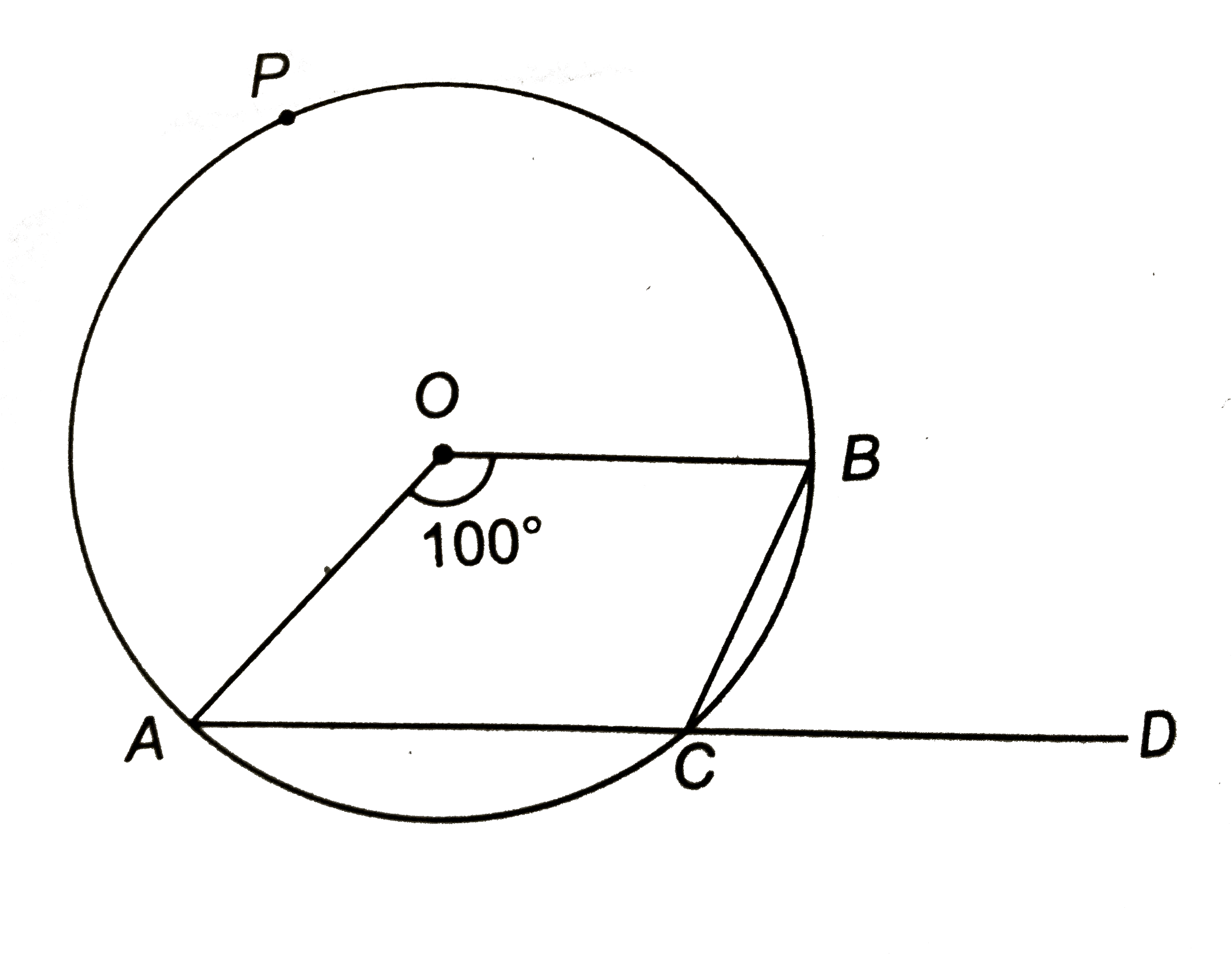
View Solutionसंलग्न चित्र में, AC वृत्त का व्यास है | यदि `angleBDC=115^(@)` , तो `angleACB` का मान ज्ञात कीजिए |
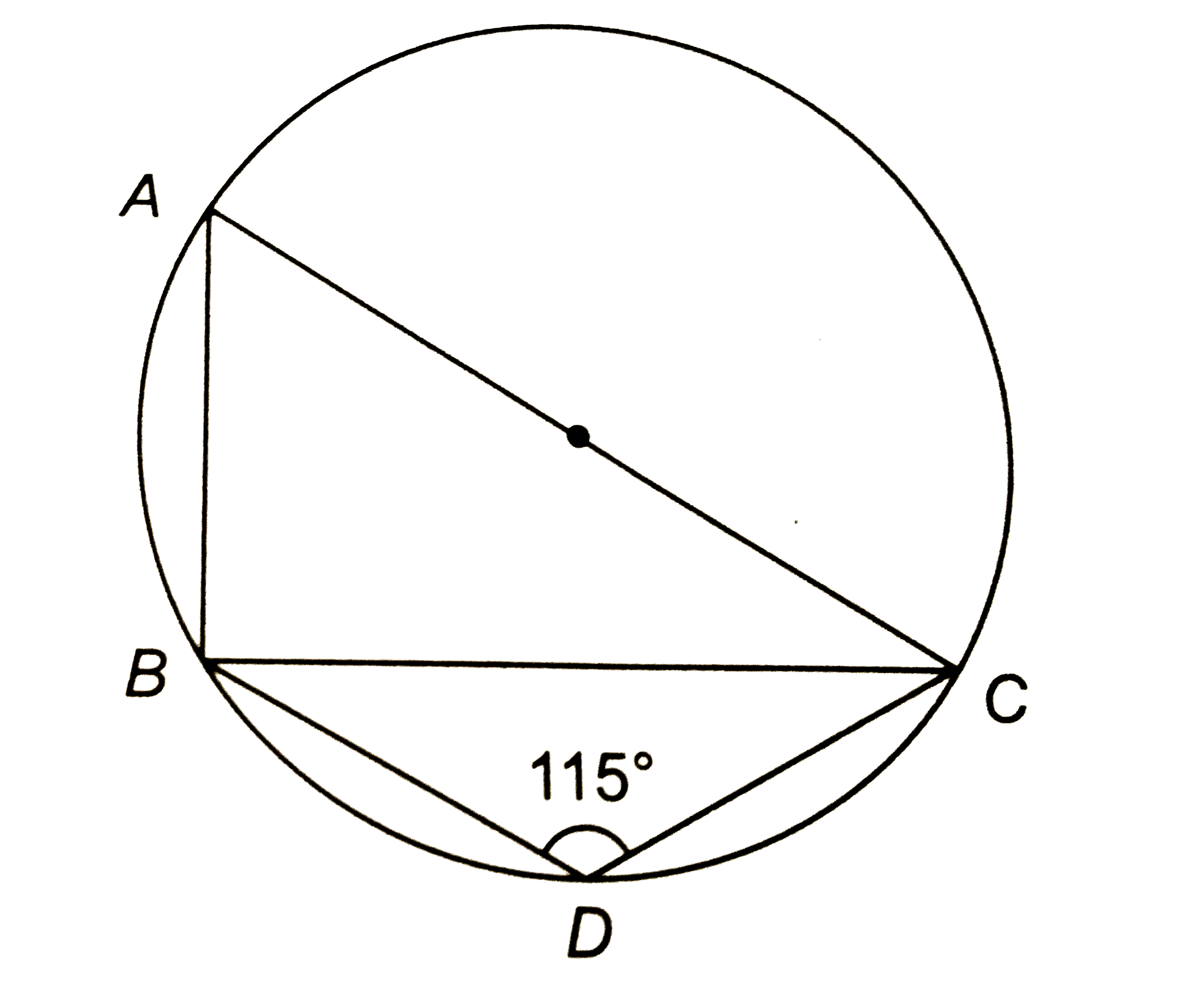
View Solutionसंलग्न चित्र में, ABCD एक चक्रीय चतुर्भुज है | यदि `angleDBC=60^(@)` और `angleBAC=40^(@)`, तो `angleBCD` का मान ज्ञात कीजिए |
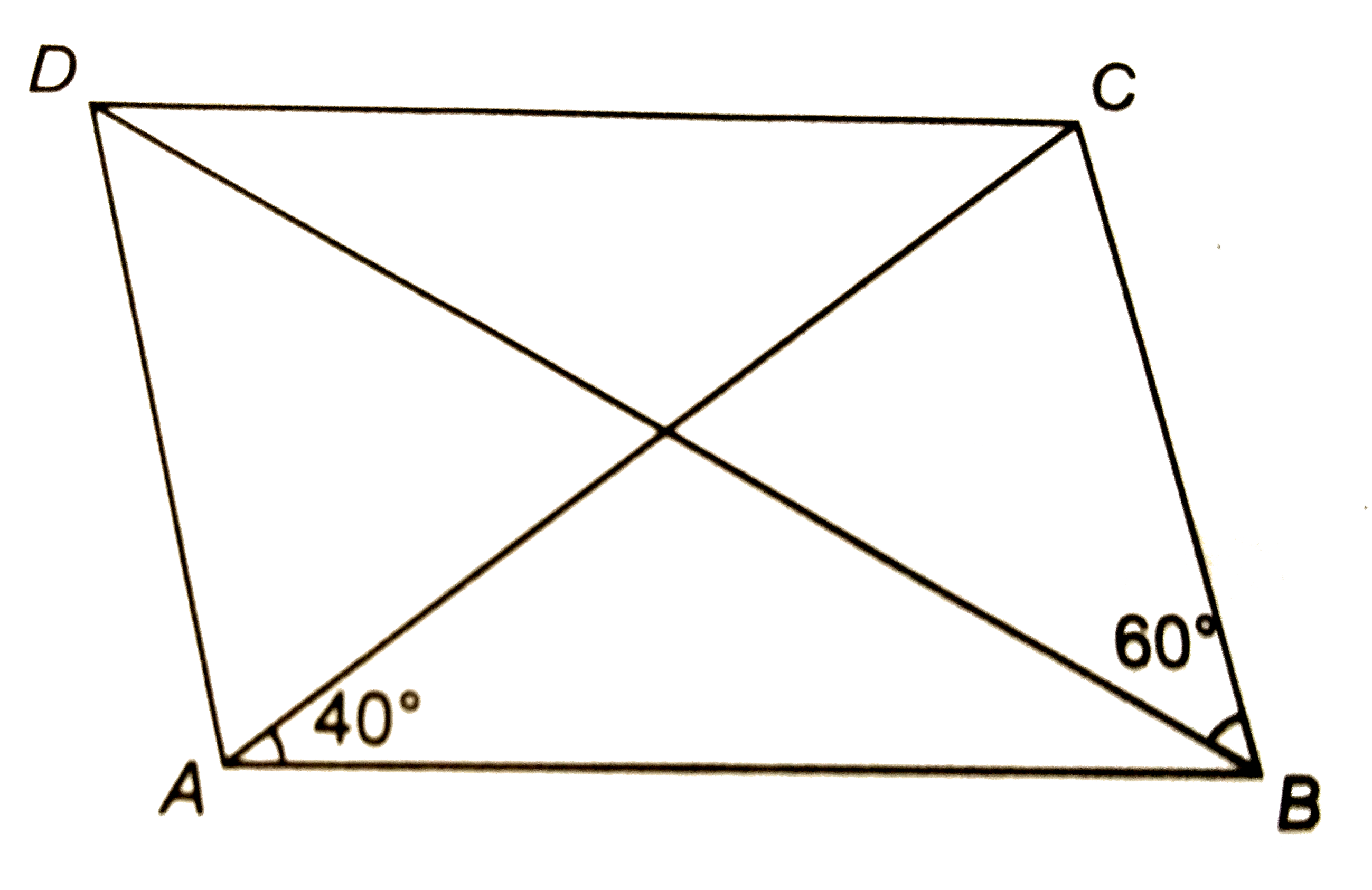
View Solutionसंलग्न चित्र में, ABCD एक चक्रीय चतुर्भुज है जिसकी भुजा AB वृत्त का एक व्यास है | यदि `angleADC=140^(@)`, तो `angleBAC` का मान ज्ञात कीजिए |
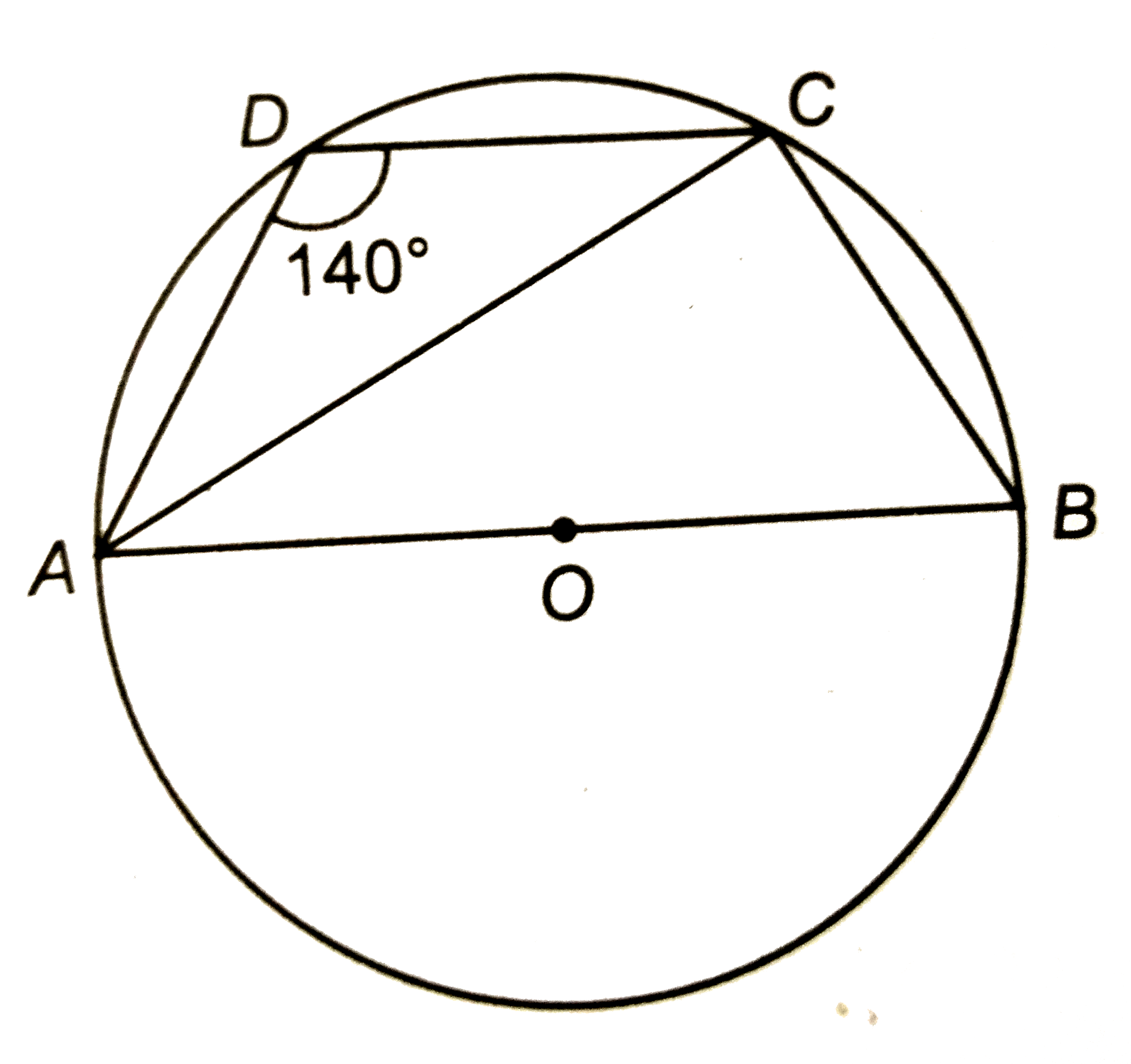
View Solutionसंलग्न चित्र में, 'O' वृत्त का केन्द्र है | यदि `angleBAD=30^(@)`, तो x, y और z के मान ज्ञात कीजिए |

View Solutionएक चक्रीय समलम्ब चतुर्भुज ABCD में भुजा AB, भुजा DC के समान्तर है | सिद्ध कीजिए कि,
भुजा AD = भुजा BC
View Solutionयदि एक चक्रीय चतुर्भुज में सम्मुख भुजाओं का एक युग्म समान है तो सिद्ध कीजिए कि इसके विकर्ण समान होंगे |
View Solutionसंलग्न चित्र में D, E और F, `DeltaPQR` की भुजाओं के मध्य बिन्दु हैं | बिन्दु P से QR पर डाले गये लम्ब का पाद 'S' है |
सिद्ध कीजिए कि,
(i) FQ = FS और `angleFQS=angleFSQ`
(ii) `angleFQS=angleFED`
(iii) `square "FSDE"` चक्रीय चतुर्भुज है |
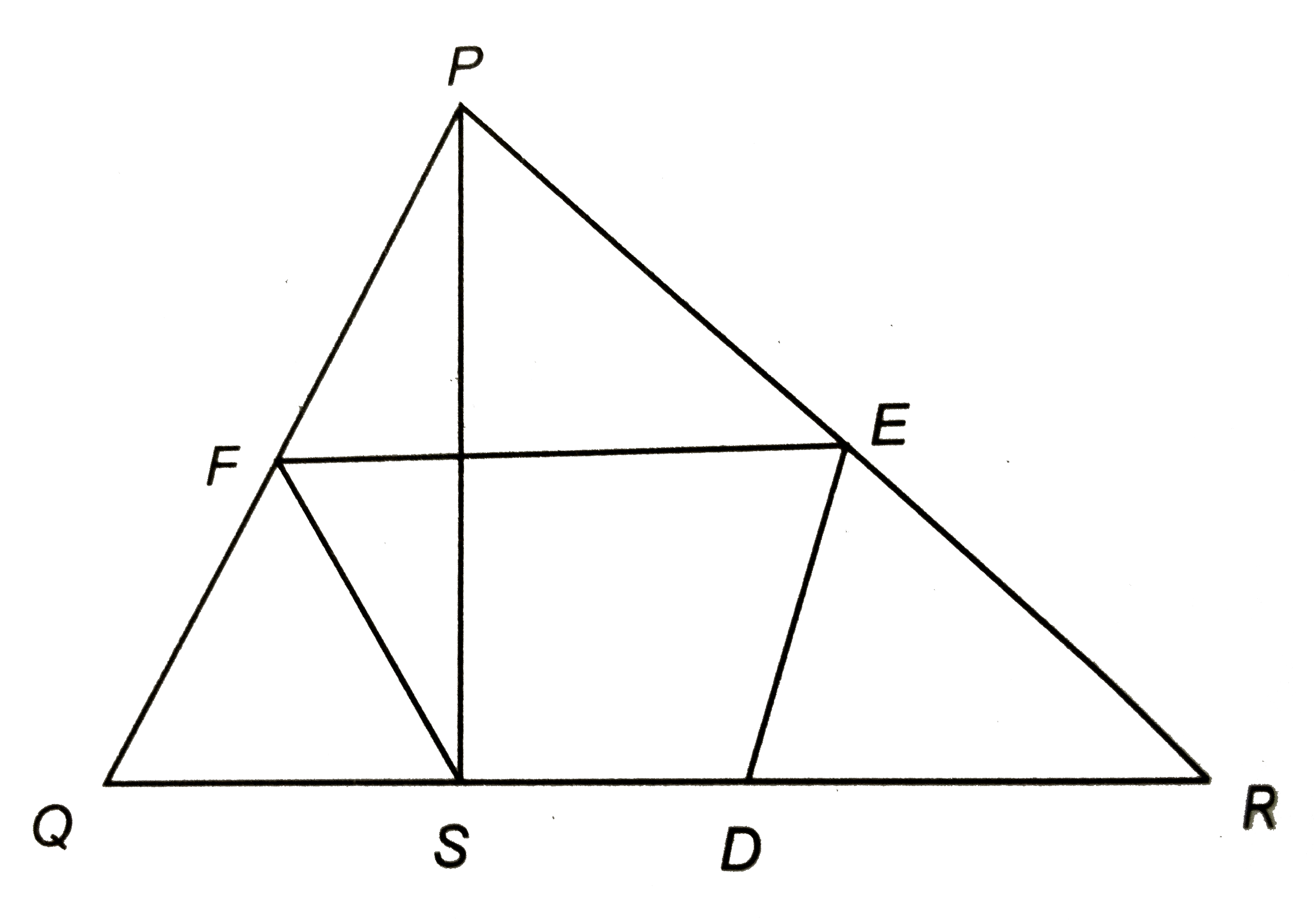
View Solutionसंलग्न चित्र में, ABCD एक चक्रीय चतुर्भुज है | यदि `angleCBX=104^(@)` और `angleCAB=56^(@)`, तो `angleADB` का मान ज्ञात कीजिए |
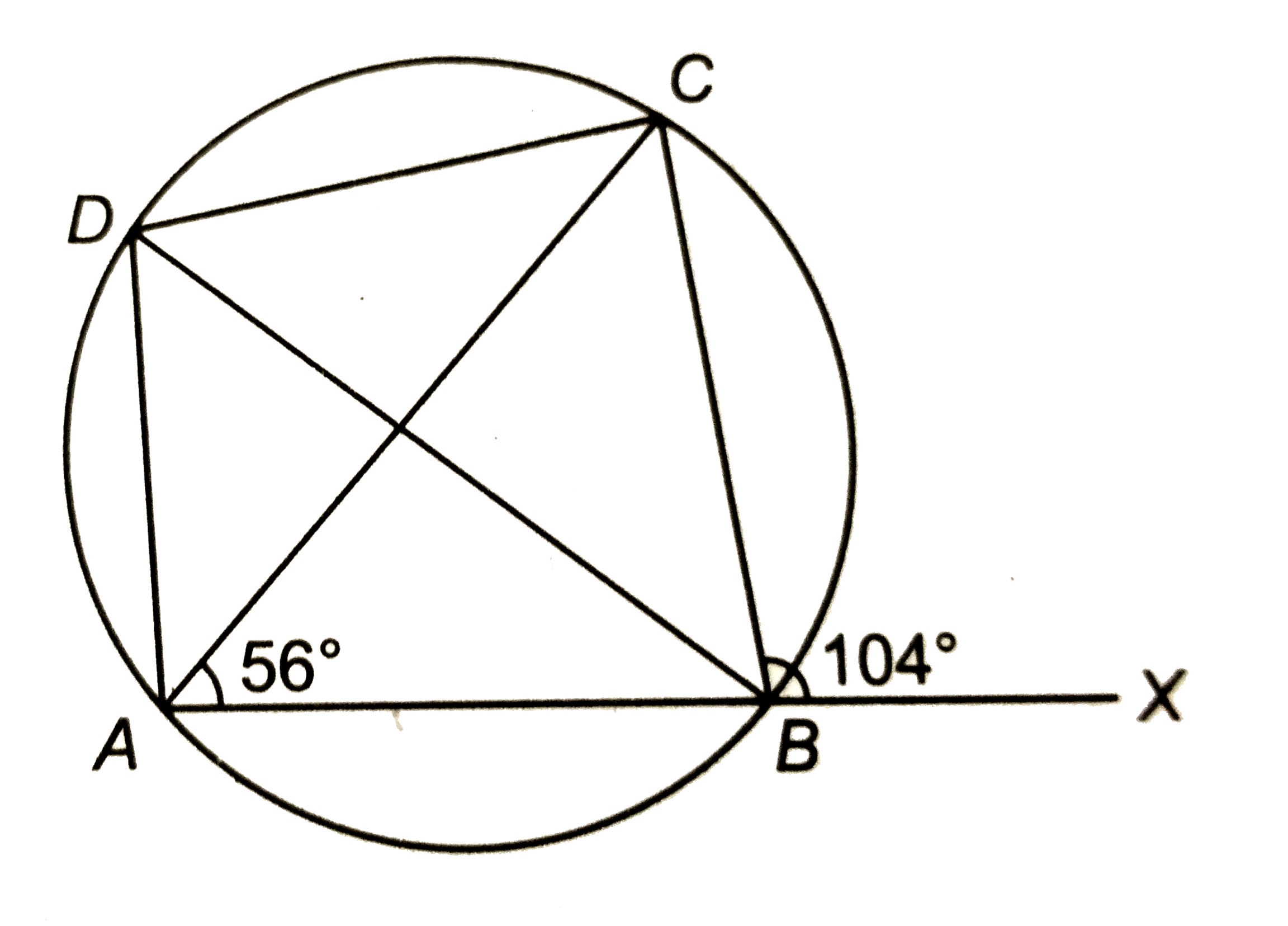
View Solution`square"ABCD"` एक चक्रीय समलम्ब चतुर्भुज है जिसमें `"AB"||"DC"` है | यदि `angleB=75^(@)`, तो अन्य कोण ज्ञात कीजिए |
View Solutionचक्रीय चतुर्भुज ABCD की भुजाओं AB और DC को बढ़ाने पर वे बिन्दु E पर मिलती हैं | इसी प्रकार भुजाओं CB और DA को बढ़ाने पर वे बिन्दु F पर मिलती हैं | यदि `angleBEC=38^(@)` और `angleBAD=102^(@)`, तो `angleAFB` और `angleADC` के मान ज्ञात कीजिए |
View SolutionABCD एक समान्तर चतुर्भुज है | A, B और C से होकर जाने वाला वृत्त CD (या बढ़ाई गई CD) को E पर काटता है | सिद्ध कीजिए कि AE = AD.
View Solutionसिद्ध कीजिए कि त्रिभुज की शीर्षों से सम्मुख भुजाओं पर डाले गये लम्ब संगामी होते हैं |
View Solutionएक वृत्त समान्तर चतुर्भुज ABCD की भुजा AD को P पर और बढ़ाई गई BC को Q पर काटता है | सिद्ध कीजिए कि `squarePDQC` चक्रीय है |
View Solution
साधित उदाहरण questions and complete solutions for chapter वृत्त of NAGEEN MATHS (HINDI) of Class 9
All Exercises from MADHUR GUPTA Class 9 MATHS वृत्त
- एन०सी०ई०आर०टी० प्रश्न (प्रश्नावली 10.1)
- एन०सी०ई०आर०टी० प्रश्न (प्रश्नावली 10.2)
- एन०सी०ई०आर०टी० प्रश्न (प्रश्नावली 10.3)
- एन०सी०ई०आर०टी० प्रश्न (प्रश्नावली 10.4)
- एन०सी०ई०आर०टी० प्रश्न (प्रश्नावली 10.5)
- एन०सी०ई०आर०टी० प्रश्न (प्रश्नावली 10.6 ऐच्छिक)
- प्रश्नावली 10A
- प्रश्नावली 10B
- प्रश्नावली 10C
- विविध प्रश्नावली (अतिलघु उत्तरीय प्रश्न)
- विविध प्रश्नावली (दीर्ध उत्तरीय प्रश्न)
- विविध प्रश्नावली (लघु उत्तरीय प्रश्न)
- साधित उदाहरण