Complete Solutions to Solved Examples of chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREAS OF PARALLELOGRAMS AND TRIANGLES |
| RS AGGARWAL | Solved Examples |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
Show that the segment joining the mid-points of a pair of opposite sides of a parallelogram, divides it into two equal parallelograms.
View SolutionThe diagonals of a parallelogram `A B C D` intersect at `Odot` A line through `O` meets `A B\ ` in `x\ a n d\ C D` in `Ydot` Show that `a r\ (A X Y X)=1/2(a r|""|^(gm)\ \ A B C D)`
View SolutionShow that a median of a triangle divides it into two triangles of equal area.
View SolutionTwo triangles on the same base (or equal bases) and between the same parallels are equal in area Now, suppose ABCD is a parallelogram whose one of the diagonals is AC

(see Fig. 9.20). Let AN ⊥ DC. Note that
` /_\ ADC ~= /_\ CBA` (Why?)
So,` ar (ADC) = ar (CBA)` (Why?)
Therefore, `ar (ADC) = 1//2 ar (ABCD) = 1//2 (DCxx AN)` (Why?)
So, area of `/_\ ADC` = 1/2 `xx base DC xx` corresponding altitude `AN`.
Dusre shabdo mei, area of a triangle is half the product of its base (or any side) and the corresponding altitude (or height). Aapko yaad hoga area of triangle ka formula Class VII ? From this formula, two triangles with same base (or equal bases) and equal areas hai toh unke corresponding altitudes equal honge. Iss result se ek theorem aati hai.
View Solution`ABC` is a triangle in which `D` is the midpoint of `BC` and `E` is the midpoint of `AD`.
Prove that `ar(triangleBED)=(1)/(4)ar(triangleABC)`.

View SolutionIn a quadrilateral ABCD, it is being given that M is the midpoint of AC. Prove that
`ar(squareABMD)=ar(squareDMBC)`.

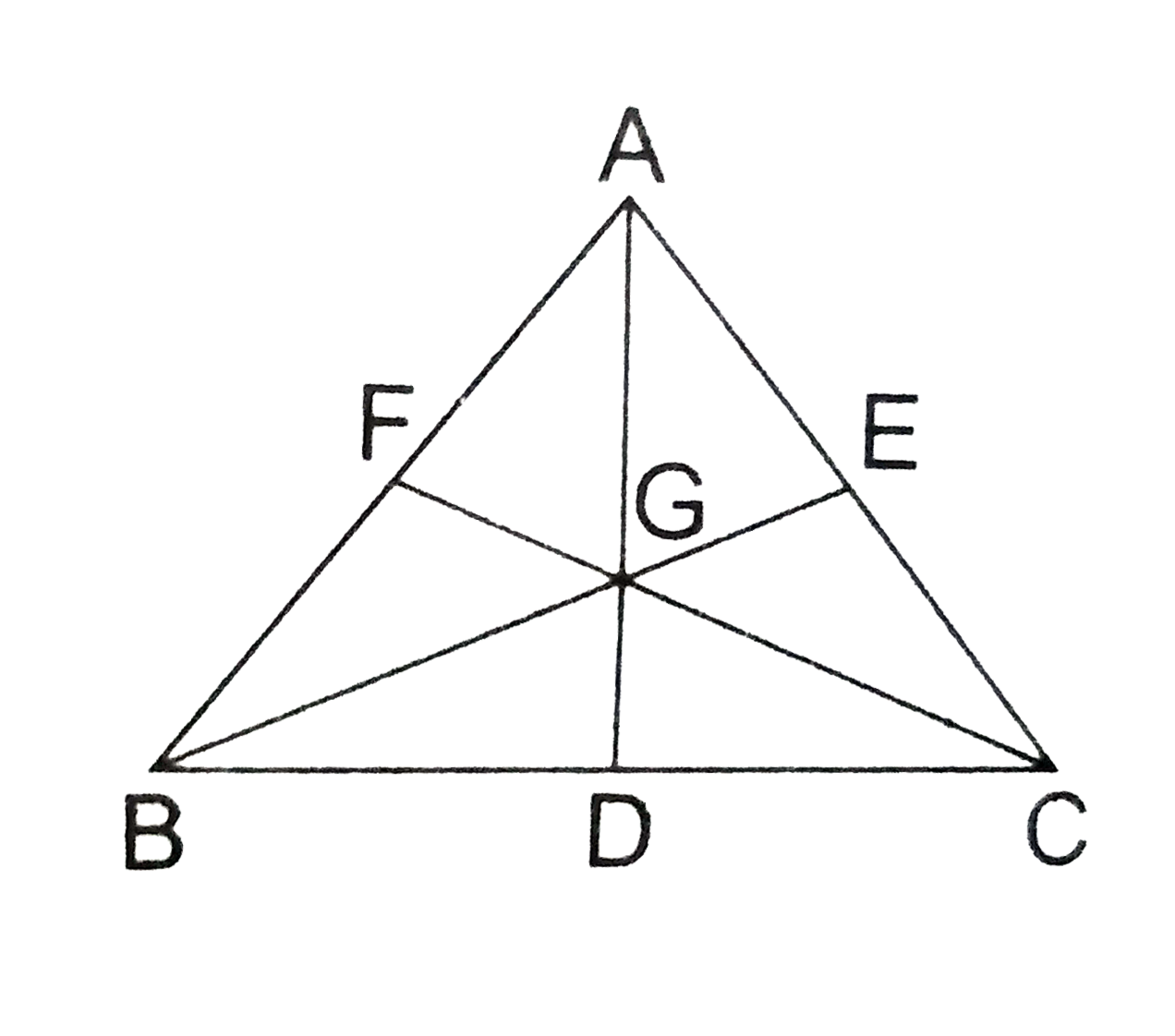
View SolutionIf the medians of a `triangle ABC` intersect at `G`, show that
`ar(triangleAGB)=ar(triangleAGC)=ar(triangleBGC)`
`=(1)/(3)ar(triangleABC)`.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionIn Figure, `A B C D` is a quadrilateral and `B E||A C` and also `B E` meets `D C` produced at `Edot` Show that area of ` A D E` is equal to the area of the quadrilateral `A B C D`
View SolutionIn `Delta ABC`, `D` is the mid-point of `AB` and `P` is any point on `BC`. If `CQ || PD` meets `AB` and `Q` (shown in figure), then prove that
`ar (DeltaBPQ) = (1)/(2) ar (DeltaABC)`.

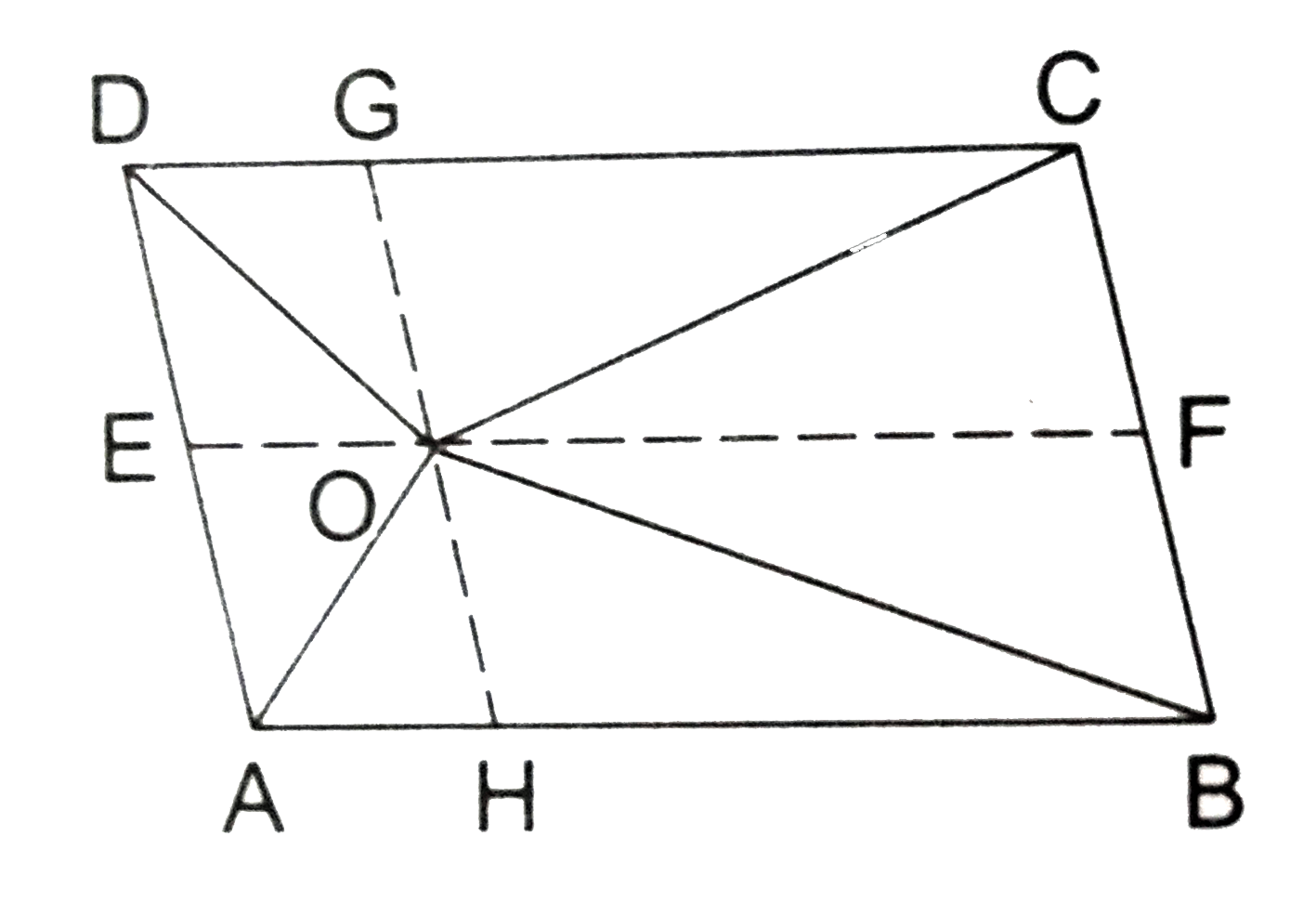
View SolutionA point `O` inside a rectangle `A B C D` is joined to the vertices. Prove that the sum of the areas of a pair of opposite triangles so formed is equal to the sum of the other pair of triangles. Given: A rectangle `A B C D\ a n d\ O` is a point inside it. `O A ,\ O B ,\ O C\ a n d\ O D` have been joined. To Prove: `a r\ (A O D)+\ a r\ ( B O C)=\ a r\ ( A O B)+\ a r( C O D)`
View SolutionABCD is a parallelogram and O is a point in its interior. Prove that
(i) `ar(triangleAOB)+ar(triangleCOD)`
`=(1)/(2)ar("||gm ABCD").`
(ii) `ar(triangleAOB)+ar(triangleCOD)=ar(triangleAOD)+ar(triangleBOC)`.
View SolutionIf each diagonals of a quadrilateral separates it into two triangles of equal area then show that the quadrilateral is a parallelogram.
View SolutionIf the diagonals `A C ,\ B D` of a quadrilateral `A B C D ,` intersect at `O ,` and separate the quadrilateral into four triangles of equal area, show that quadrilateral `A B C D` is a parallelogram.
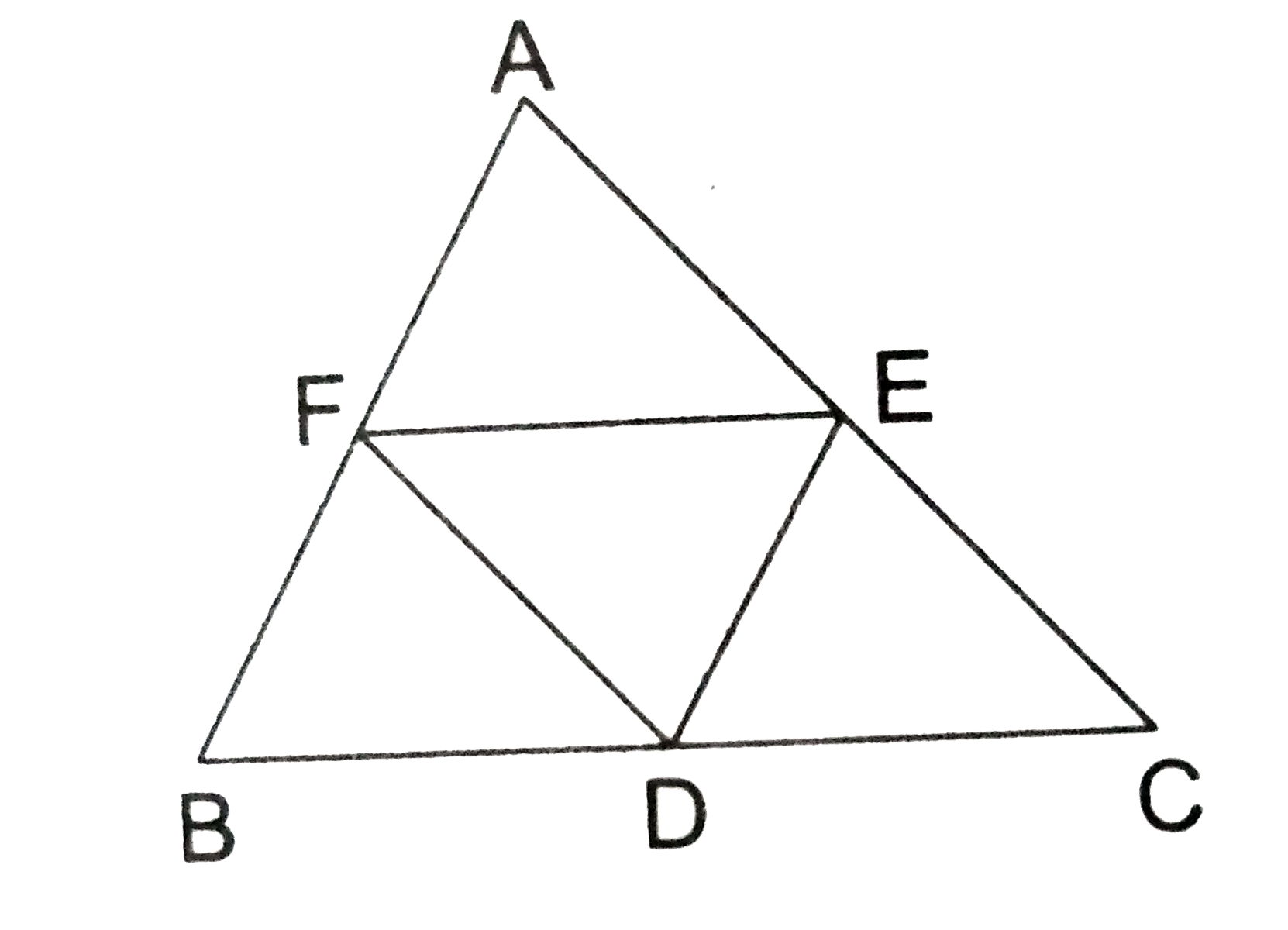
View SolutionD, E, F are the midpoints of the sides BC, CA and AB respectively of `triangle`ABC. Prove that
(i) BDEF is a ||gm,
(ii) `ar(triangleDEF)=(1)/(4) ar(triangleABC) and`
(iii) `ar("||gm BDEF") = (1)/(2)ar(triangleABC)`
View SolutionIn Figure, `A B C D E\ ` is a pentagon. A line through `B` parallel to `A C` meets `D C` produced at `Fdot` Show that: `a r\ ( A C B)=a r\ ( A C F)` `a r\ (A E D F)=a r\ (A B C D E)`
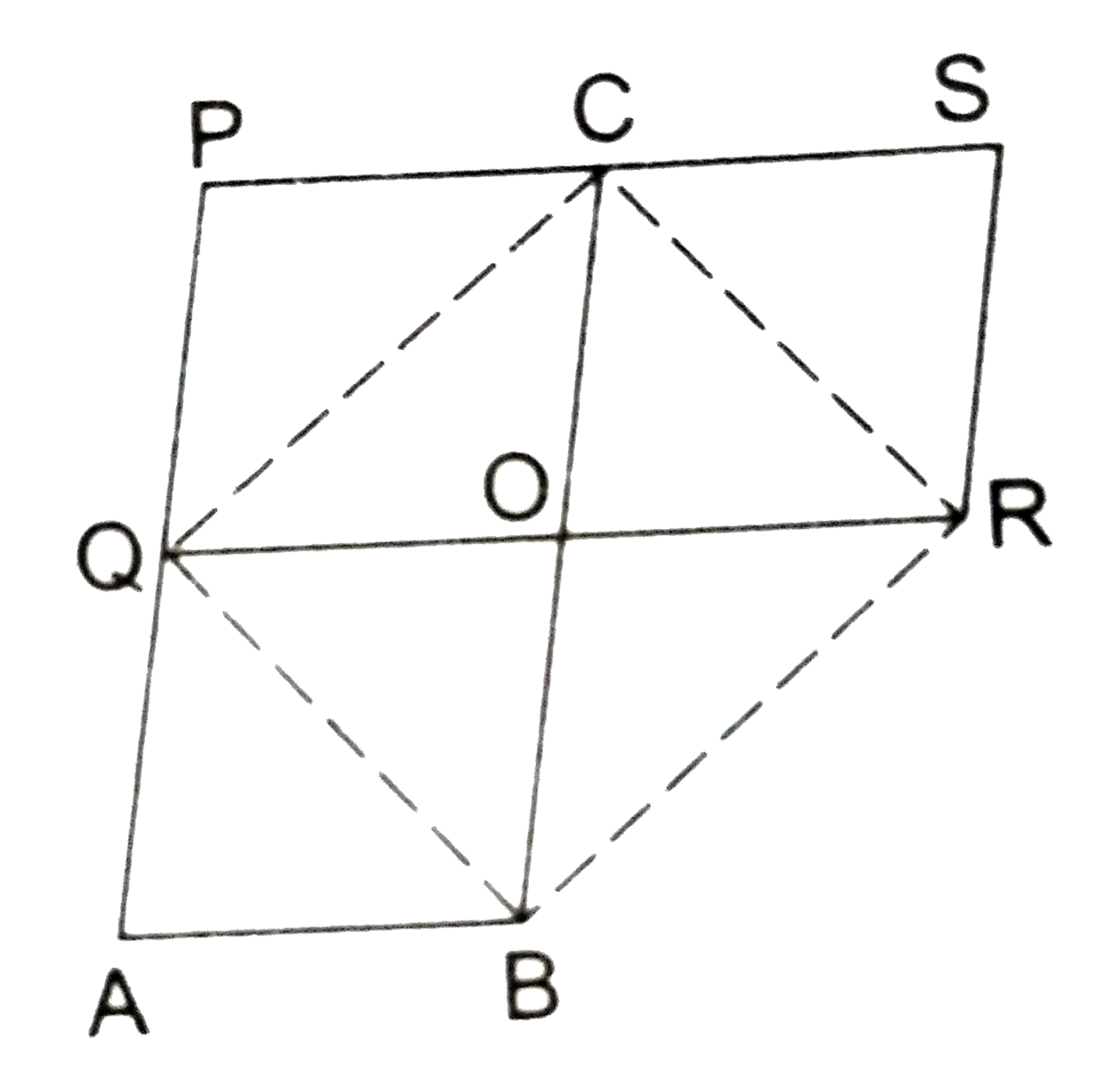
View SolutionIn the adjoining figure, PQRS and PABC are two parallelogram of equal area. Prove that QC||BR.
View SolutionIn figure, `CD || AE` and `CY || BA`. Prove that `ar (DeltaCBX) = ar (DeltaAXY)`.

View SolutionIn the adjoining figure, ABCD is a parallelogram and P is any points on BC. Prove that
`ar(triangleABP)+ar(triangleDPC)=ar(trianglePDA)`.
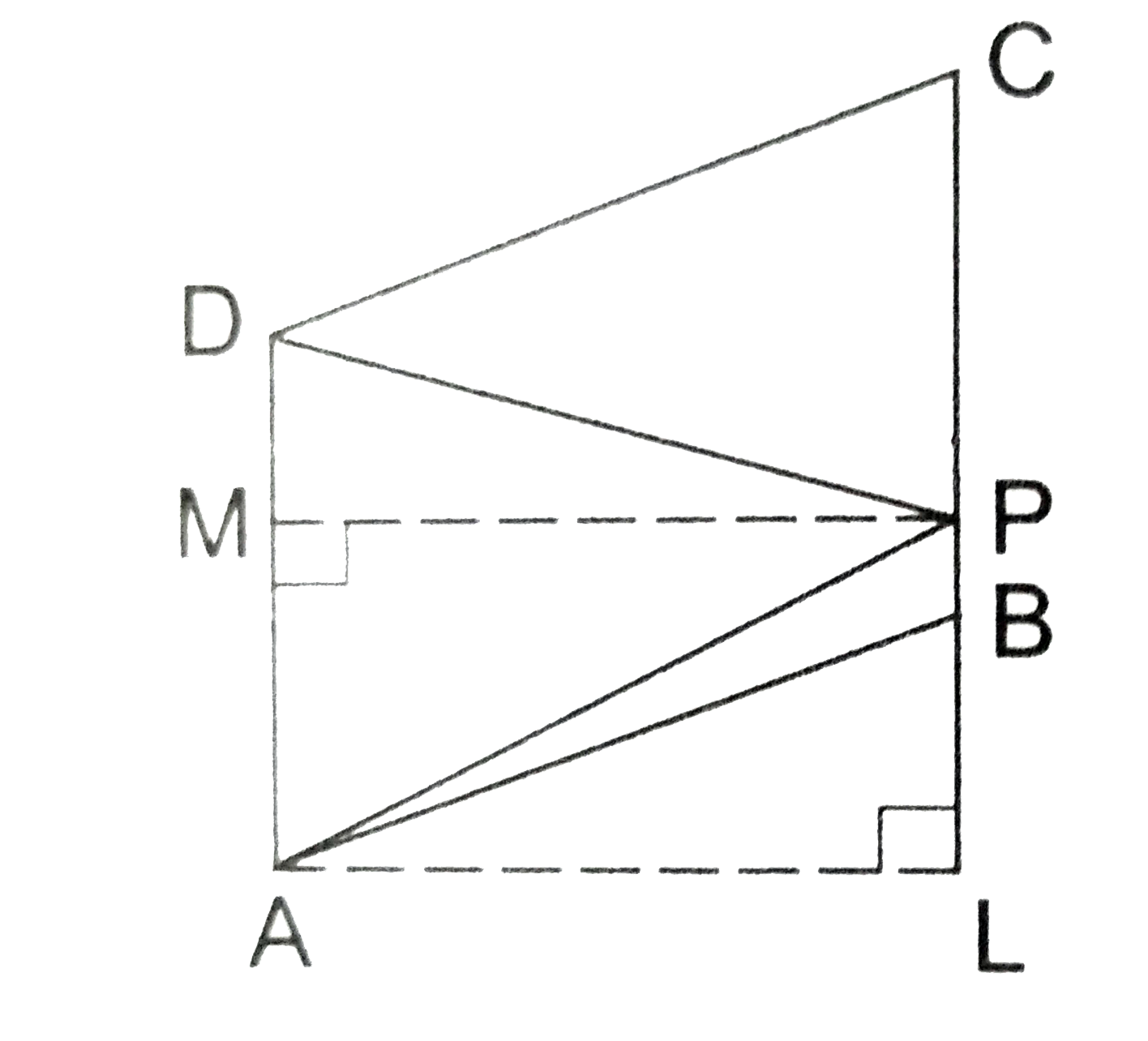
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that `ar (DeltaPEA) = ar (DeltaQFD)`.
View SolutionThe side `A B` of a parallelogram `A B C D` is produced to any point `Pdot` A line through `A` and parallel to `C P` meets `C B` produced at `Q` and then parallelogram `P B Q R` is completed as shown in Figure. Show that `a r(|"|"hatgm\ A B C D)=a r\ (|""|^(gm)P B Q R)`
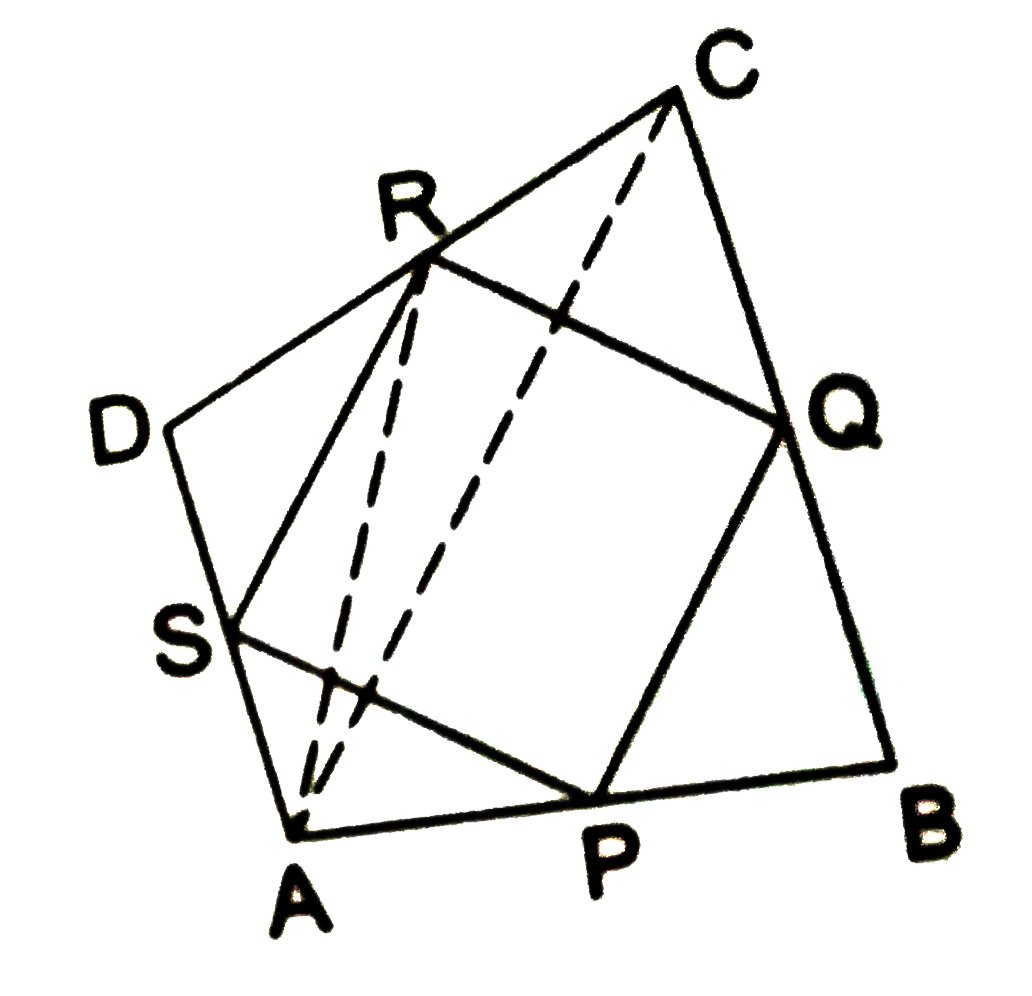
View SolutionLet P, Q, R, S be respectively the midpoints of the sides AB, BC, CD and DA of quad. ABCD Show that PQRS is a parallelogram such that
`ar("||gm PQRS")=(1)/(2)ar("quad. ABCD")`.
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that `ar (DeltaPEA) = ar (DeltaQFD)`.

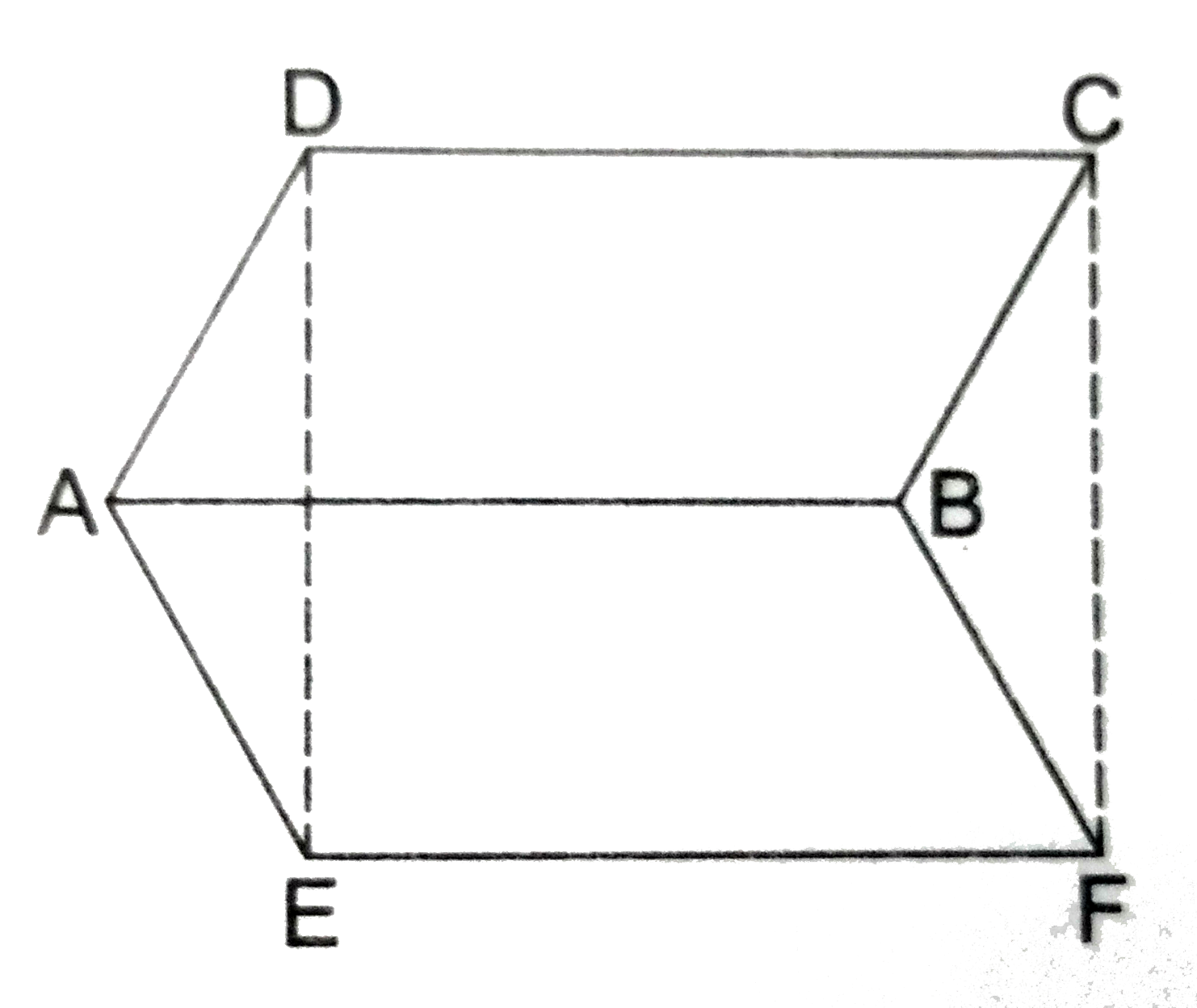
View SolutionIn the adjoing figure, two parallelograms ABCD and AEFB are drawn on opposite sides of AB. Prove that
`ar("||gm ABCD") +ar("||gm AEFB")`
`=ar("||gm EFCD")`.
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that `ar (DeltaPEA) = ar (DeltaQFD)`.

View SolutionProve that of all parallelograms of which the sides are given, the parallelogram which is rectangle has the greatest area.
View SolutionParallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View SolutionX and Y are points on the side LN of the triangle LMN such that LX = XY = YN. Through X, a line is drawn parallel to LM to meet MN at Z (see figure). Prove that `ar (DeltaLZY) = ar (MZYX)`.
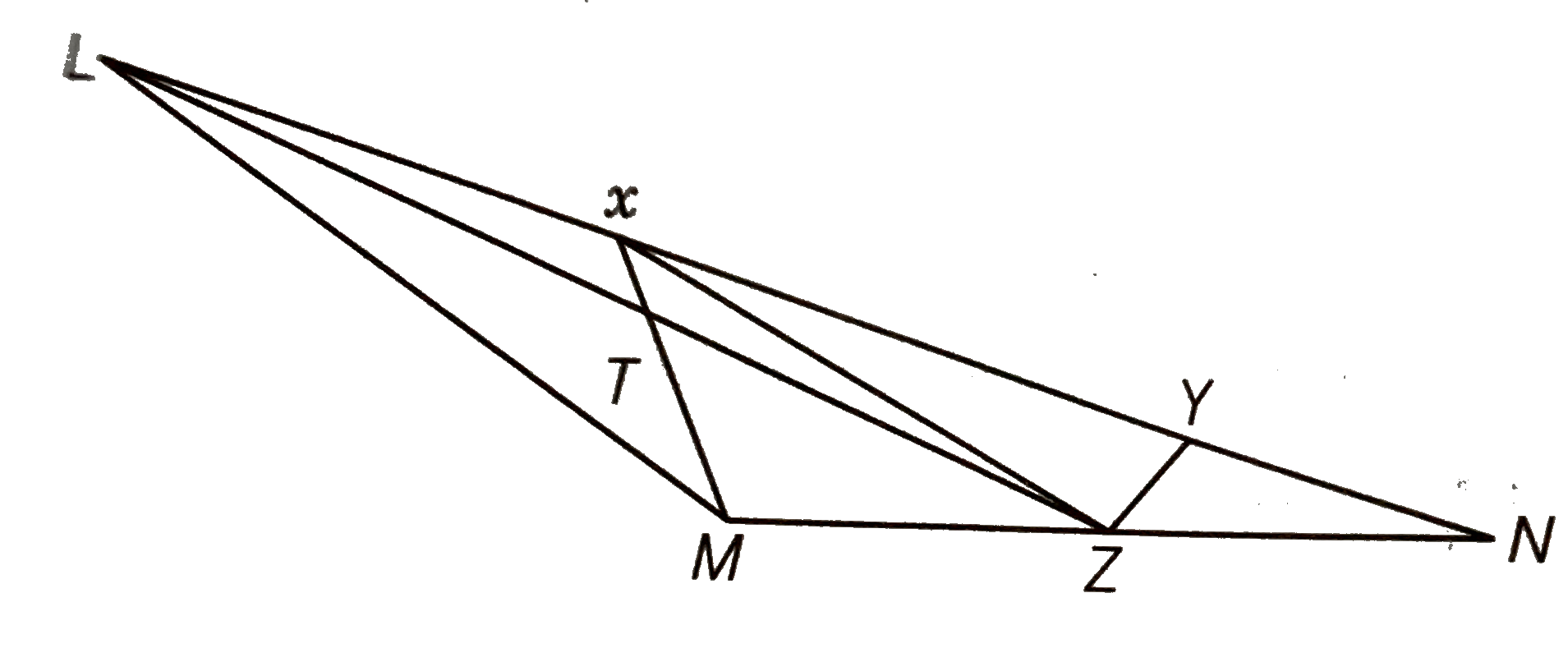
View SolutionIn the adjoining figure, ABCD is a parallelogram. Points P and Q on BC trisect BC. Prove that
`ar(triangleAPQ)=ar(triangleDPQ)=(1)/(6)ar(triangleABCD)`.

View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
`(i) ar(triangleBDE)= (1)/(4)ar(triangleABC)`
`(ii) ar(triangleBDE)=(1)/(2)ar(triangleBAE)`
`(iii) ar(triangleABC)=2ar(triangleBEC)`
`(iv) ar(triangleBFE)=ar(triangleAFD)`
`(v)ar(triangleBFE)=2ar(triangleFED)`
`(vi) ar(triangleFED)=(1)/(8)ar(triangleAFC)`.

View Solution
Solved Examples questions and complete solutions for chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of RS AGGARWAL MATHS (HINGLISH) of Class 9