Complete Solutions to Exercise 11 of chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREAS OF PARALLELOGRAMS AND TRIANGLES |
| RS AGGARWAL | Exercise 11 |
| Number Of Questions | 38 |
| Academic Year | 2023-24 |
Which of the following figure lie in the same base and between the same parallels. In such a case, write the common base and the two parallels.
View SolutionIn the adjoining figure, show that ABCD is a parallelogram.
Calculate the area of ||gm ABCD.
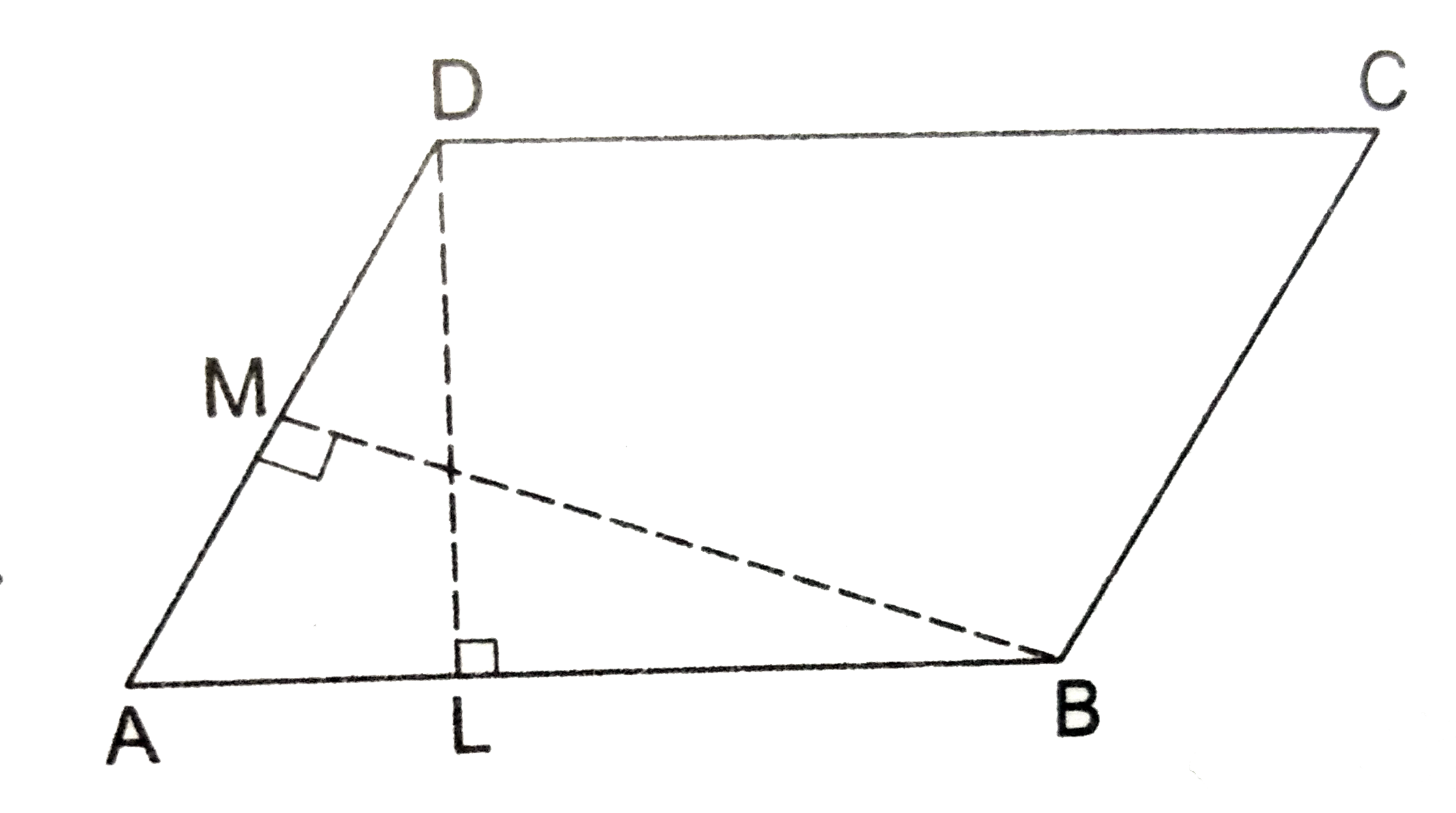
View SolutionIn a parallelogram ABCD, it is being given that AB = 10 cm and the altitudes corresponding to the sides AB and AD are DL = 6 cm and BM = 8 cm, respectively. Find AD.
View SolutionThe lengths of the diagonals of a rhombus are 12 cm and 16 cm. Find the area of rhombus
View SolutionFind the area of a trapezium whose parallel sides are 9 cm and 6cm respectively and the distance between these sides is 8 cm.
View SolutionCalculate the area of quad. ABCD, given in til (ii) Calculate the area of trap. PQRS,
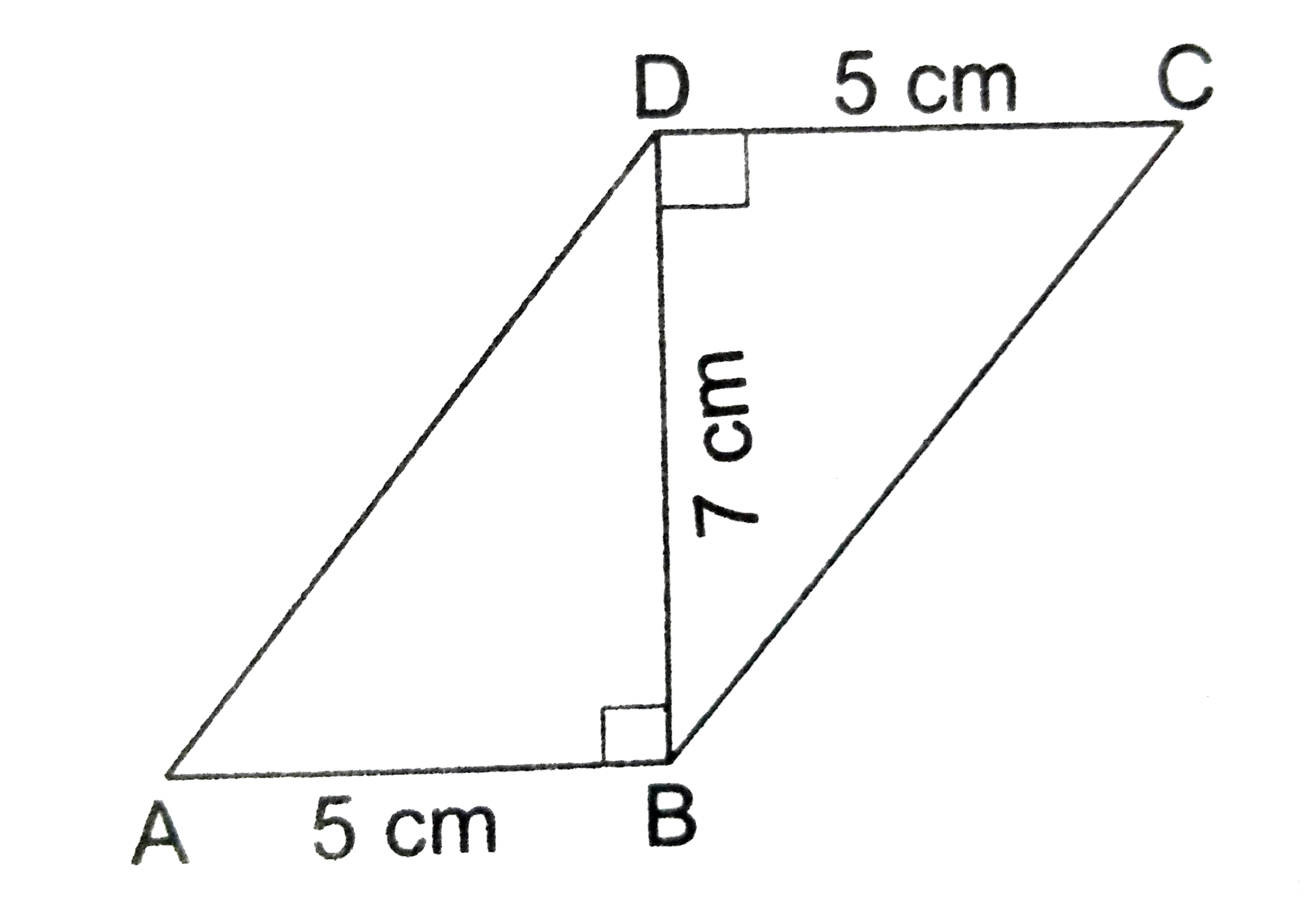
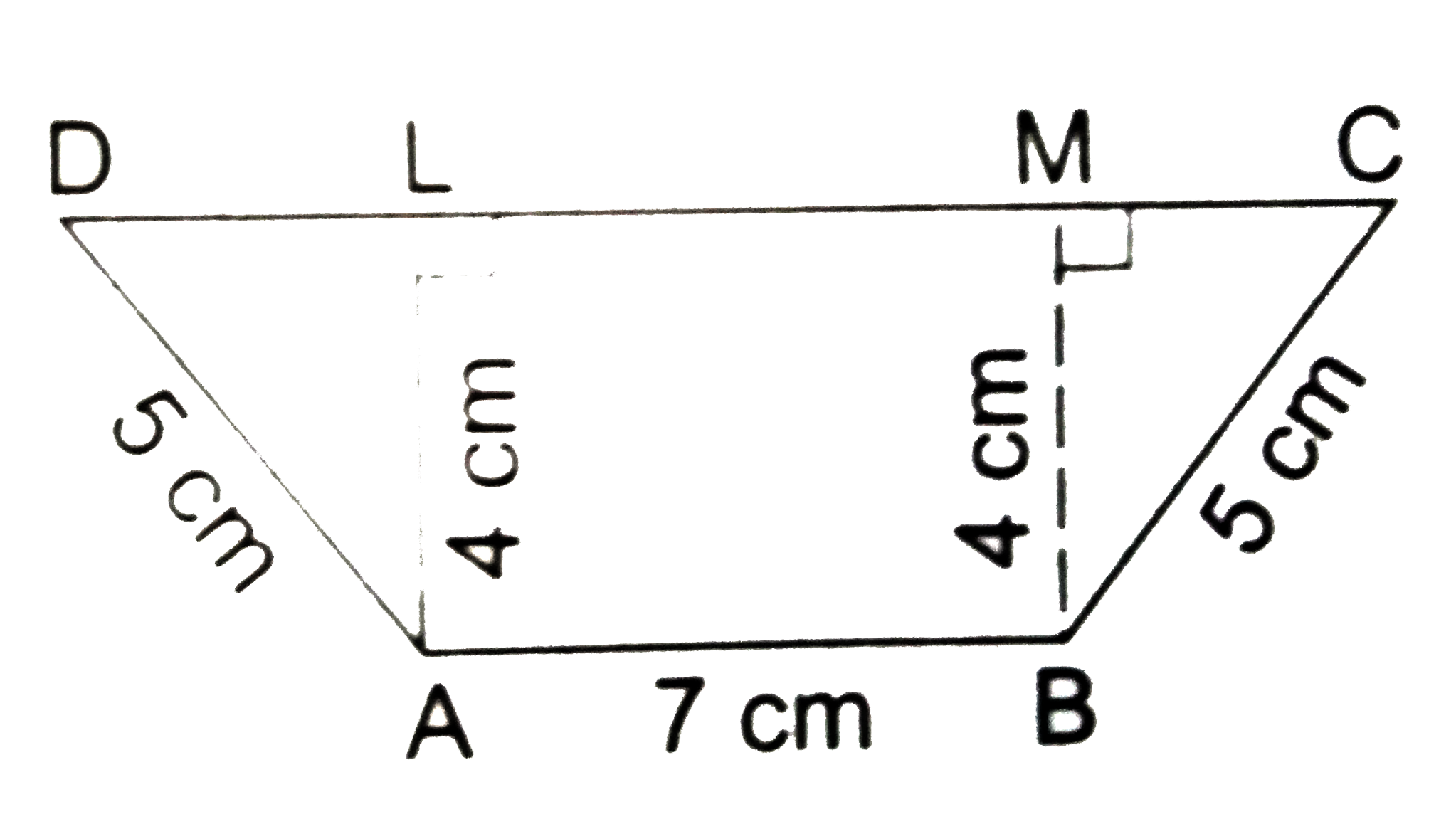
View SolutionIn the given figure, ABCD is a trapezium such that `AL bot DC and BM bot DC`. If AB = 7 cm, BC = AD = 5 cm and AL = BM = 4 cm then ar(trap. ABCD) = ?
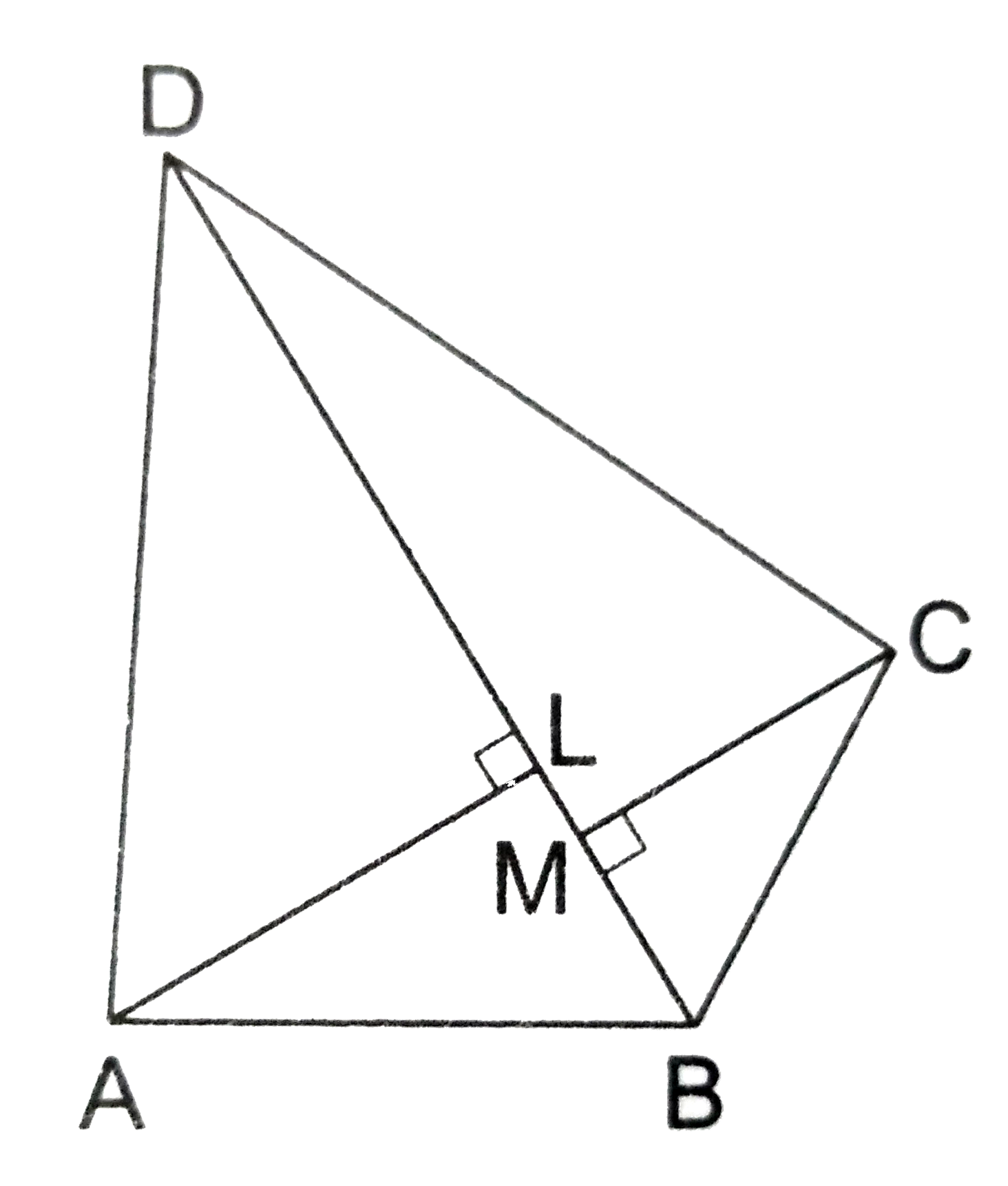
View SolutionBD is one of the diagonals of a quad. ABCD. If `ALbotBD and CMbotBD`, show that
`ar("quad. ABCD")=(1)/(2)xxBDxx(AL + CM)`.
View SolutionABCD is a parallelogram and X is the mid-point of AB. `(AXCD)= 24 cm^(2)`, then `ar (ABC) = 24 cm^(2)`.
View SolutionIn the adjoining figure, ABCD is a quadrilateral in which diag. BD = 14 cm. If `ALbotBD and CMbotBD` such that AL = 8 cm and CM = 6 cm, find the area of quad. ABCD.

View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogramABCD. Show that `a r\ (A P B)\ =\ a r\ (B Q C)`.
View SolutionIn the adjoining figure, MNPQ and ABPQ are parallelogram and T is any point on the side BP. Prove that
(i) `ar(MNPQ)=ar(ABPQ)`
(ii)` ar(triangleATQ)=(1)/(2)ar(MNPQ)`.

View SolutionAssertion (A) : In a trapezium ABCD, we have AB ||DC and the diagonals AC and BD intersect at O.
Then, `ar(triangleAOD)= ar(triangleBOC)`.

Reason (R ) : Triangle on the same base between the same parallels are equal in area.
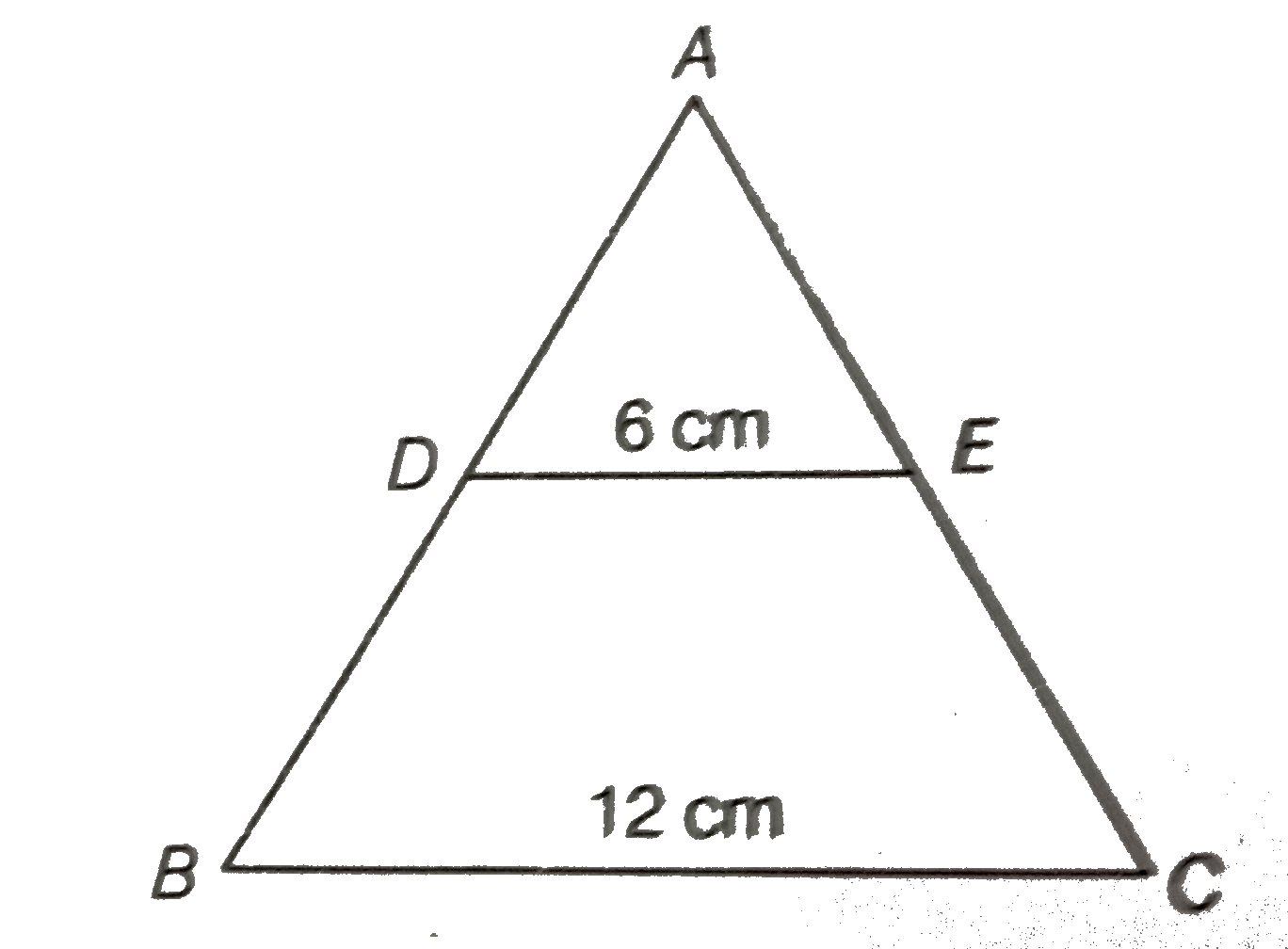
View SolutionIn figure, if DE`abs()`BC, then find the ratio of ar (`DeltaADE`) and ar(DECB).
View SolutionShow that a median of a triangle divides it into two triangles of equal area.
View SolutionA diagonal of a parallelogram divides it into two triangles of equal area.
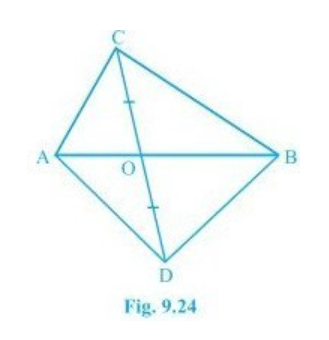
View SolutionIn Fig. 9.24, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that `ar(triangleABC)=ar(triangleABD)`
View SolutionThe points `D` and `E` are respectively located on `AB` and `AC` on the sides of `Delta ABC` such that `ar (DBC) = ar (EBC)`. Demonstrate that` DE || BC.`
View SolutionO is the any point on diagonal PR of parallelogram PQRS. Prove that Ar(PSO) = Ar(PQO)
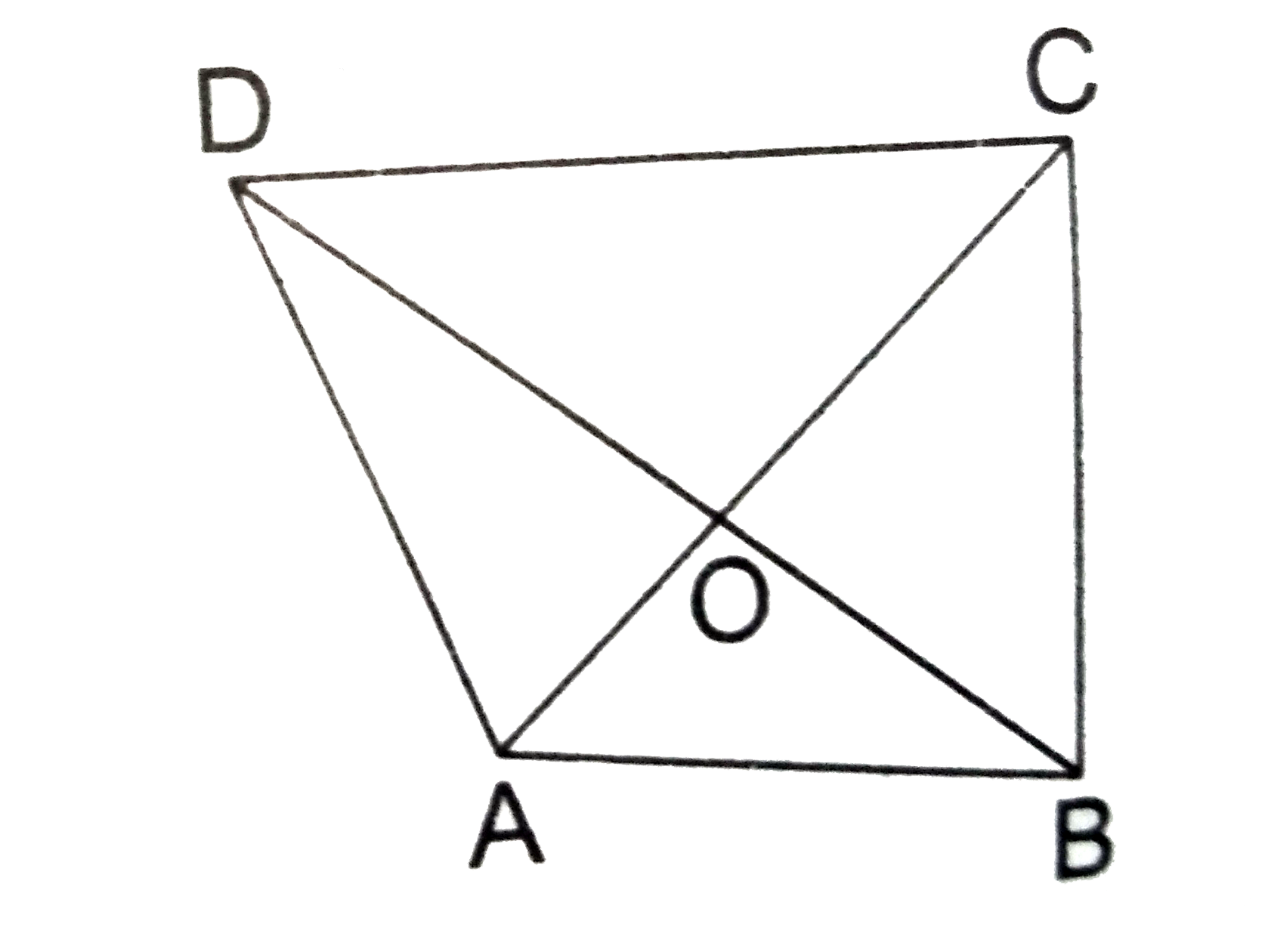
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If ` BO = OD`, prove that
`ar(triangleABC)=ar(triangleADC)`.
View SolutionThe vertex A of `triangle ABC` is joined to a point D on the side BC. The midpoint of AD is E.
Prove that `ar(triangleBEC)=(1)/(2)ar(triangleABC)`.
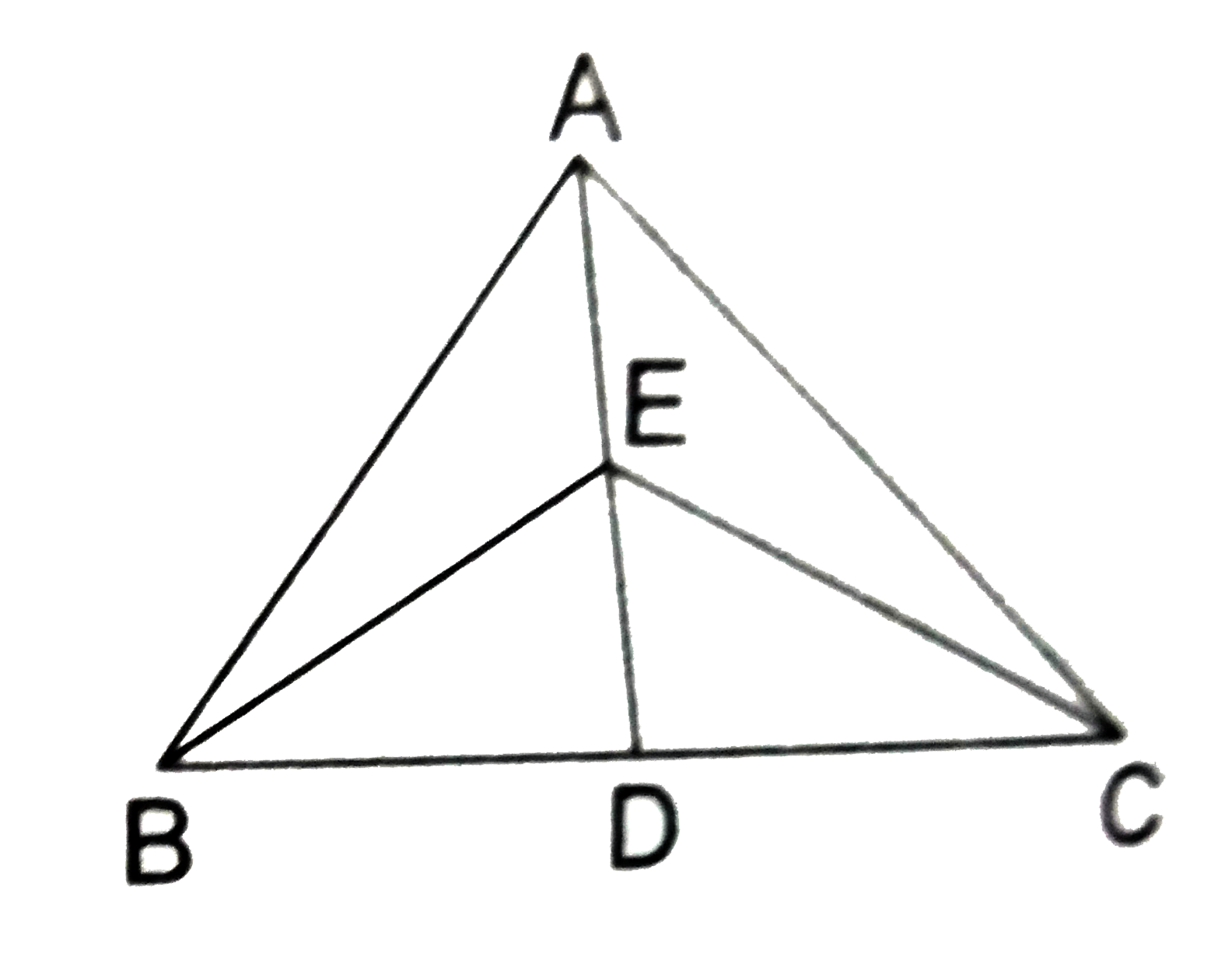
View SolutionD is the midpoint of side BC of `triangleABC` and E is the midpoint of BD. If O is the midpoint of AE,
prove that `ar(triangleBOE)=(1)/(8)ar(triangleABC)`.
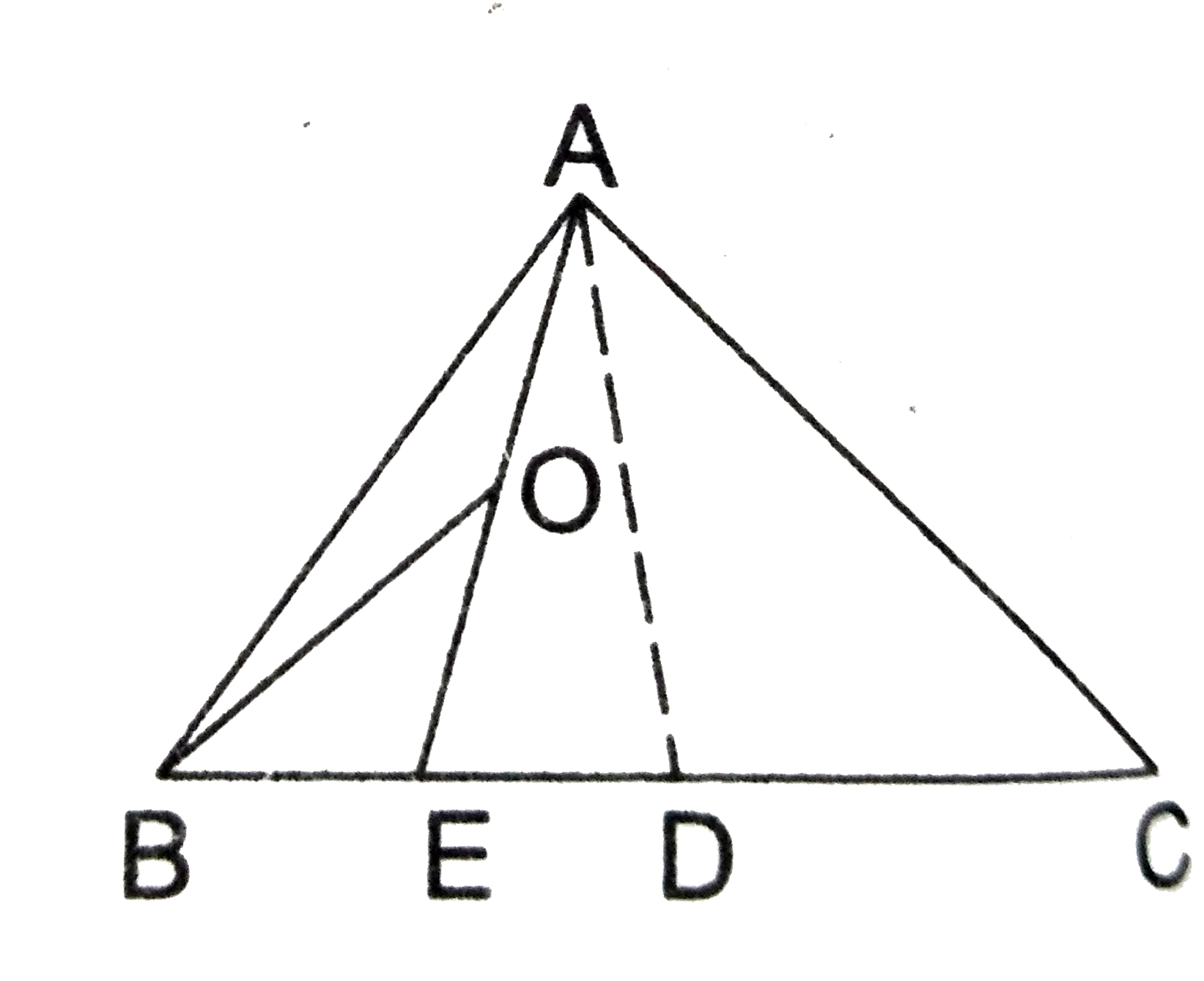
View SolutionIn trapezium ABCD, `AB || DC` and L is the mid-point of BC. Through L, a line `PQ || AD` has been drawn which meets AB in P and DC produced in Q. Prove that ar (ABCD) = ar (APQD).

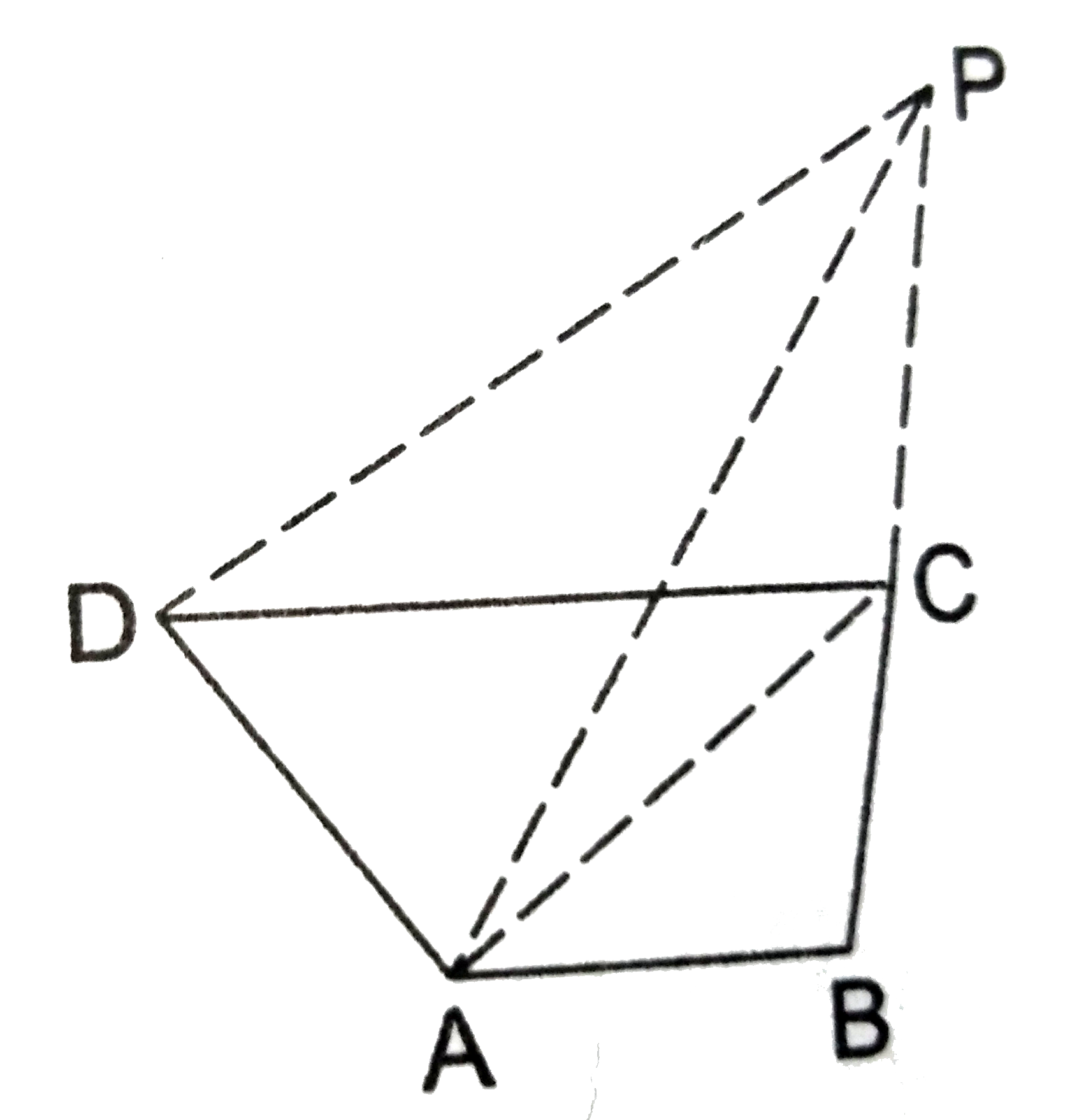
View SolutionIn the adjoining figure, ABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P .
Prove that `ar(triangleABP)=ar("qaud. ABCD")`.
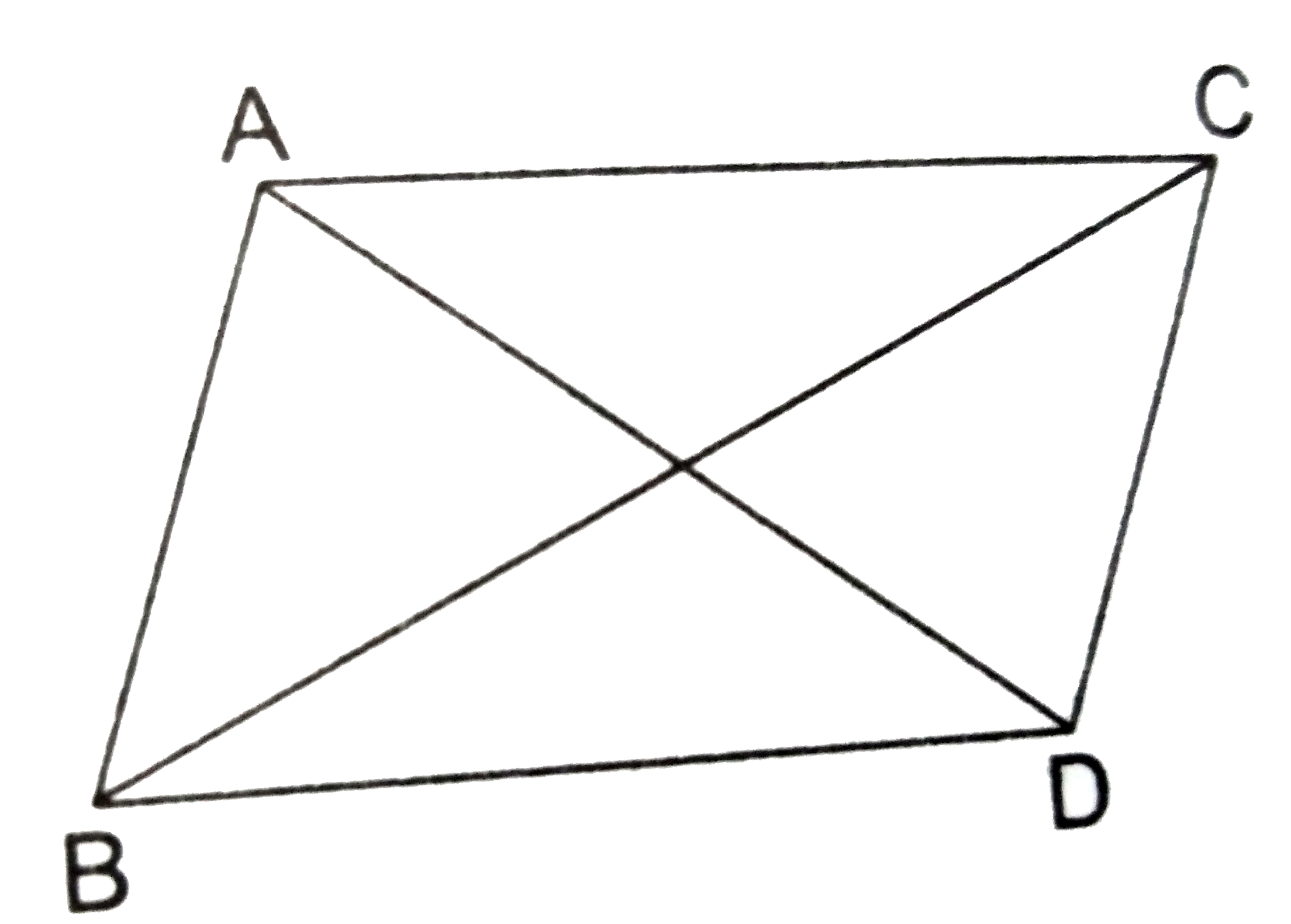
View SolutionIn the adjoining figure, `triangle ABC and triangleDBC` are on the same base BC with A and D on opposite sides of BC such that `ar(triangleABC)=ar(triangleDBC)`. Show that BC bisect AD.
View SolutionABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F.
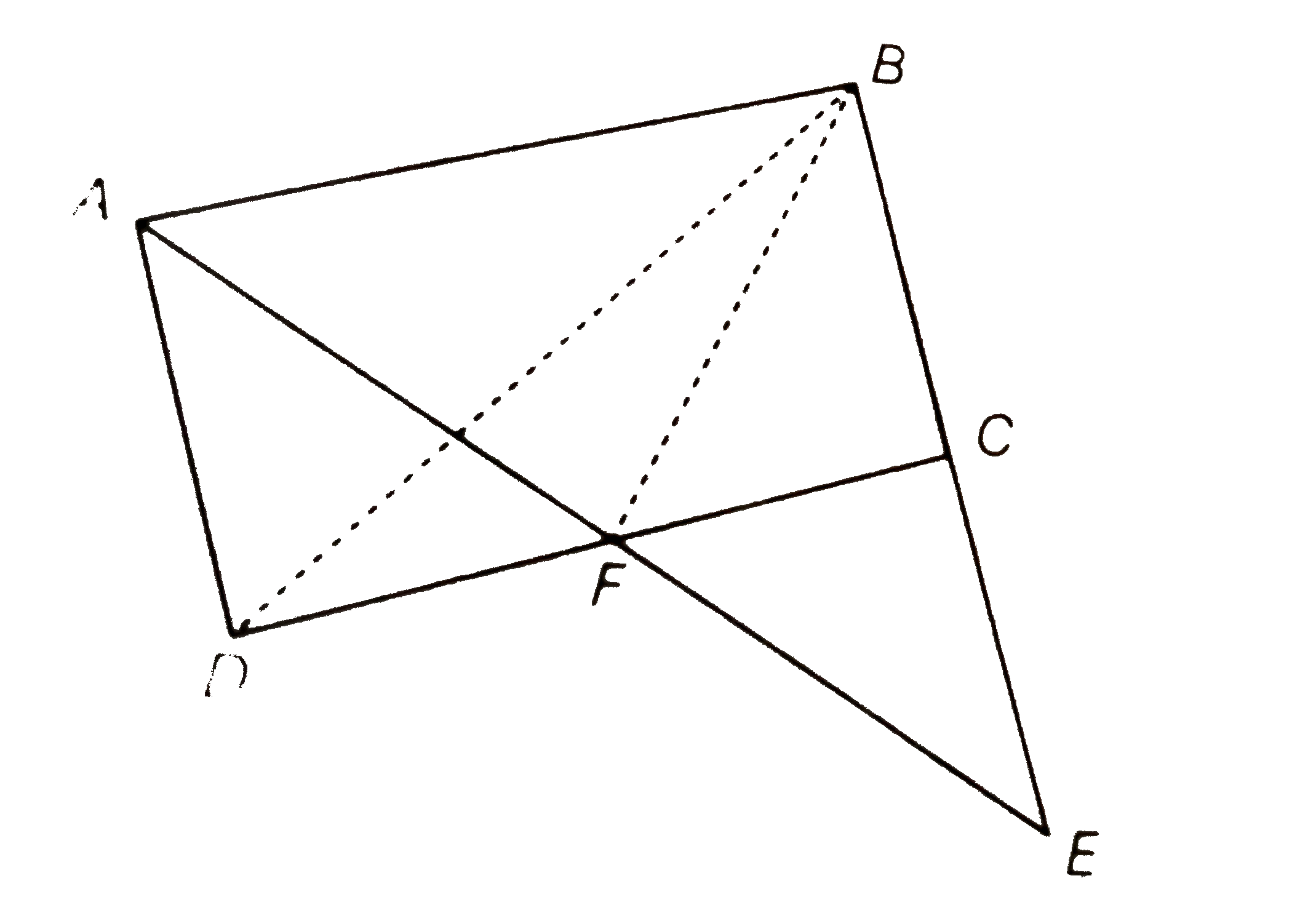
If `ar (DeltaDFB) = 3 cm^(2)`, then find the area of the parallelogram ABCD.
View SolutionA point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that `ar(DeltaADF) = ar (ABFC)`.
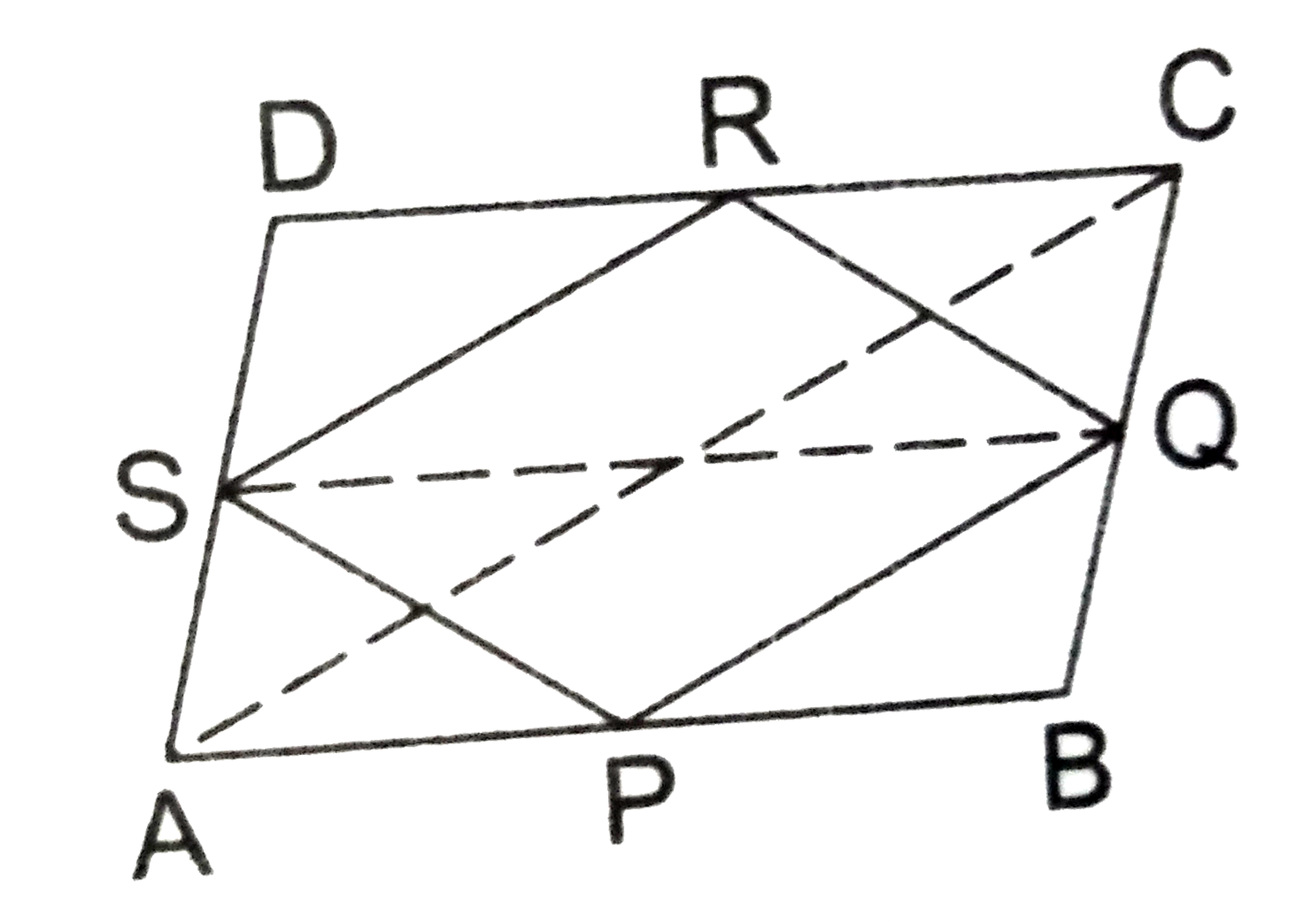
View SolutionP, Q, R, S are respectively the midpoints of the sides AB, BC, CD and DA of ||gm ABCD. Show that PQRS is a parallelogram and also show that
`ar("|| gm PQRS")=(1)/(2)xxar("||gm ABCD)`.
View Solutionकिसी त्रिभुज ABC की मधिकाएँ CD और BE एक दूसरे को O पर कटती है , तो अनुपात Ar `triangle`ODE:Ar `triangle`ABC किसके बराबर होगा ?
View SolutionThe base BC of `Delta ABC` is divided at D, so that `BD=1/2DC`. Prove that `ar(Delta ABD)`=`1/3ar(Delta ABC)`
View SolutionIn the adjoining figure, BD||CA, E is the midpoint of CA and `BD =(1)/(2) CA`. Prove that
`ar(triangleABC)=2ar(triangleDBC)`.
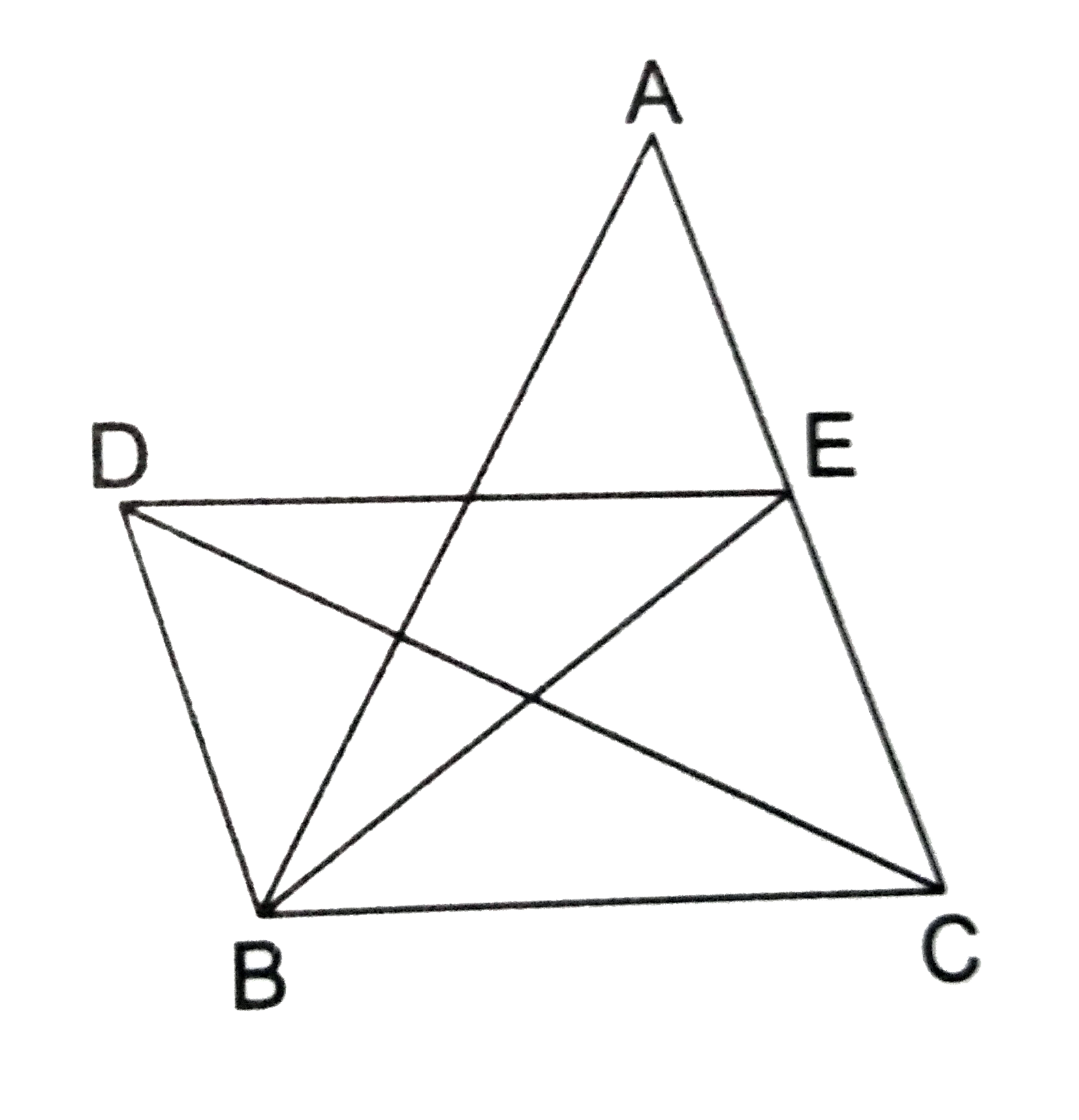
View SolutionThe given figure shows a pentagon ABCDE.EG drawn parallel to DA meets BA produced at G and CF drawn parallel to DB meets AB produced at F. Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.

View SolutionIn figure, `CD || AE` and `CY || BA`. Prove that `ar (DeltaCBX) = ar (DeltaAXY)`.

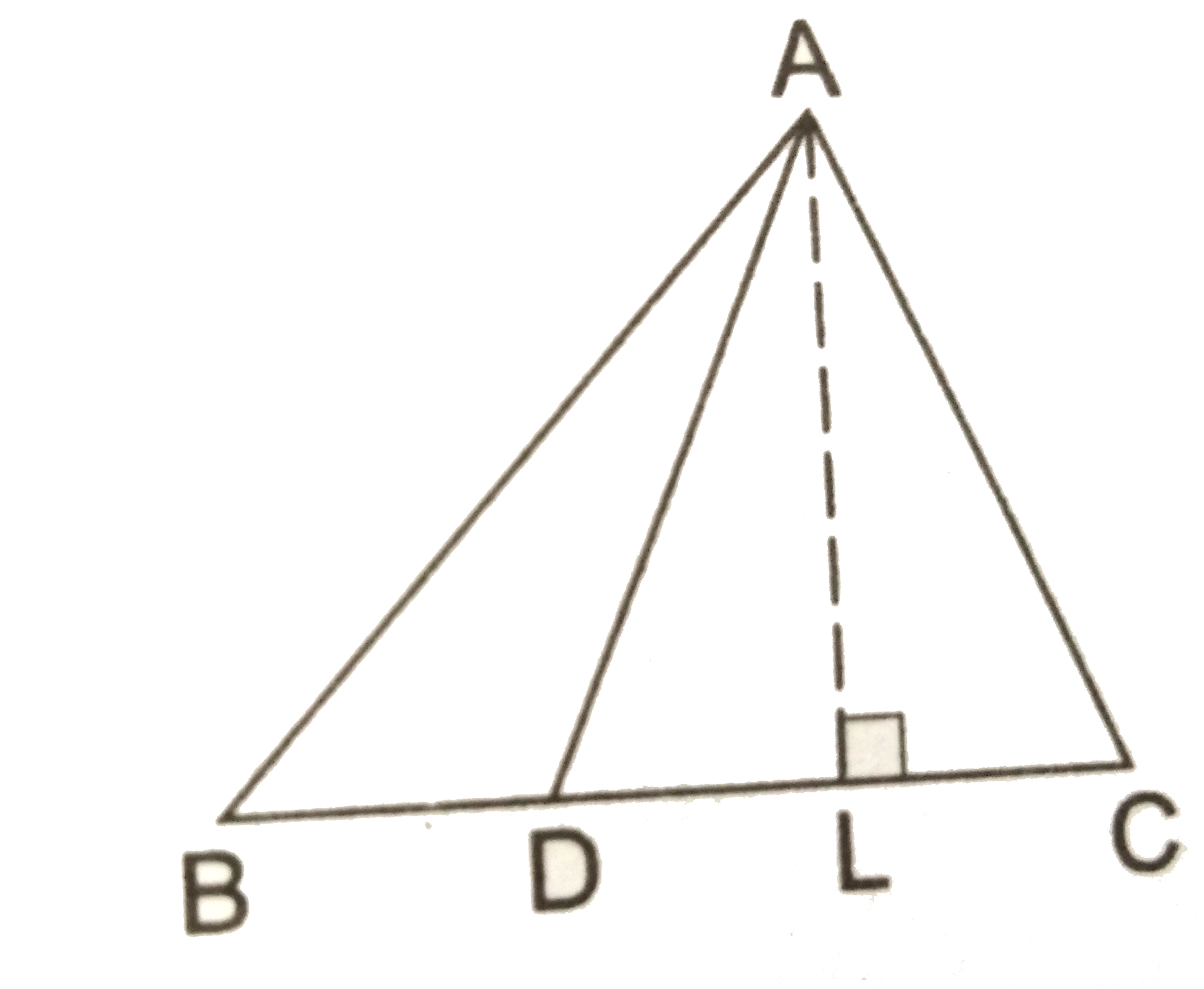
View SolutionIn the adjoining figure, the point D divides the sides of `triangleABC` in the ratio m : n. Prove that
`ar(triangleABD):ar(triangleADC) = m :n`.
View SolutionIn a trapezium ABCD, AB || DC, AB = a cm, and DC = b cm. If M and N are the midpoints of the nonparallel sides, AD and BC respectively then find the ratio of ar(DCNM) and ar(MNBA).
View SolutionABCD is a trapezium in which AB || DC, AB = 16 cm and DC = 24 cm. If E and Fare respectively the midpoints of AD and BC, prove that ar(ABFE) = `9/11` ar(EFCD).
View SolutionIn figure X and Y are the mid-points of AC and AB respectively, `QP || BC` and CYQ and BXP are straight lines. Prove that `ar (DeltaABP) = ar (DeltaACQ)`.

View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that `ar (DeltaPEA) = ar (DeltaQFD)`.
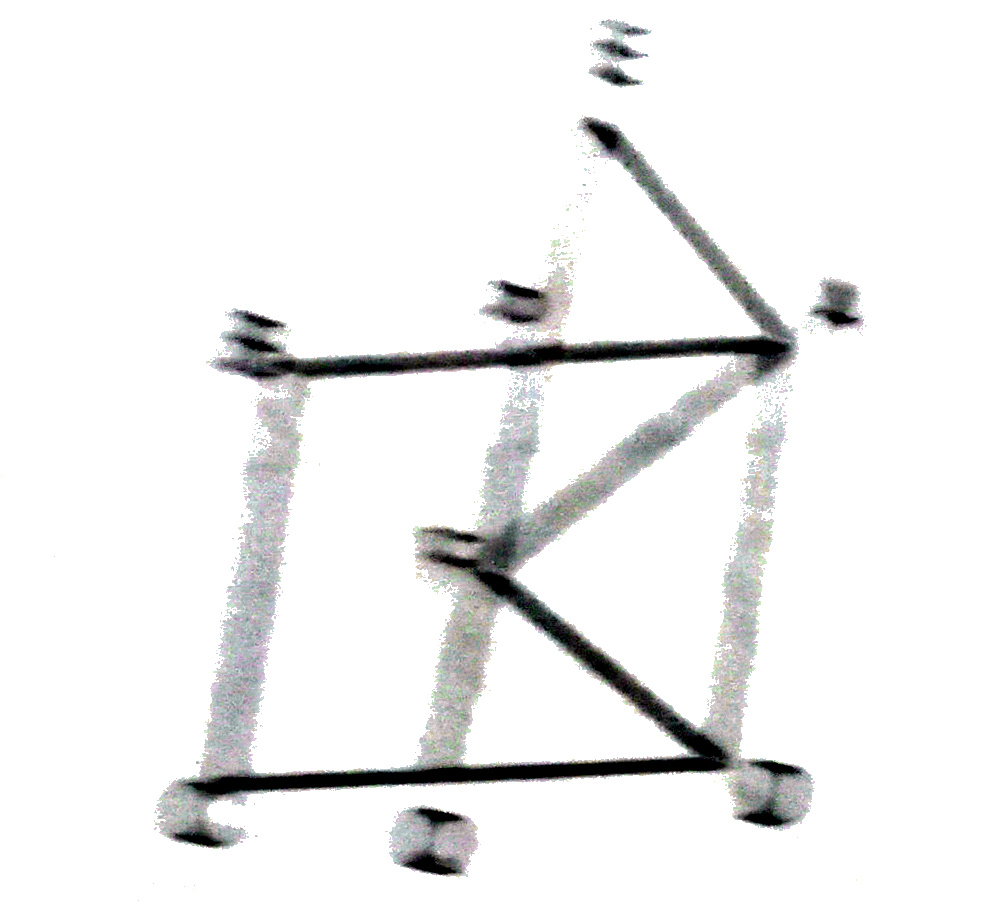
View Solution
Exercise 11 questions and complete solutions for chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of RS AGGARWAL MATHS (HINGLISH) of Class 9