Complete Solutions to EXERCISE 12C of chapter CIRCLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | CIRCLES |
| RS AGGARWAL | EXERCISE 12C |
| Number Of Questions | 26 |
| Academic Year | 2023-24 |
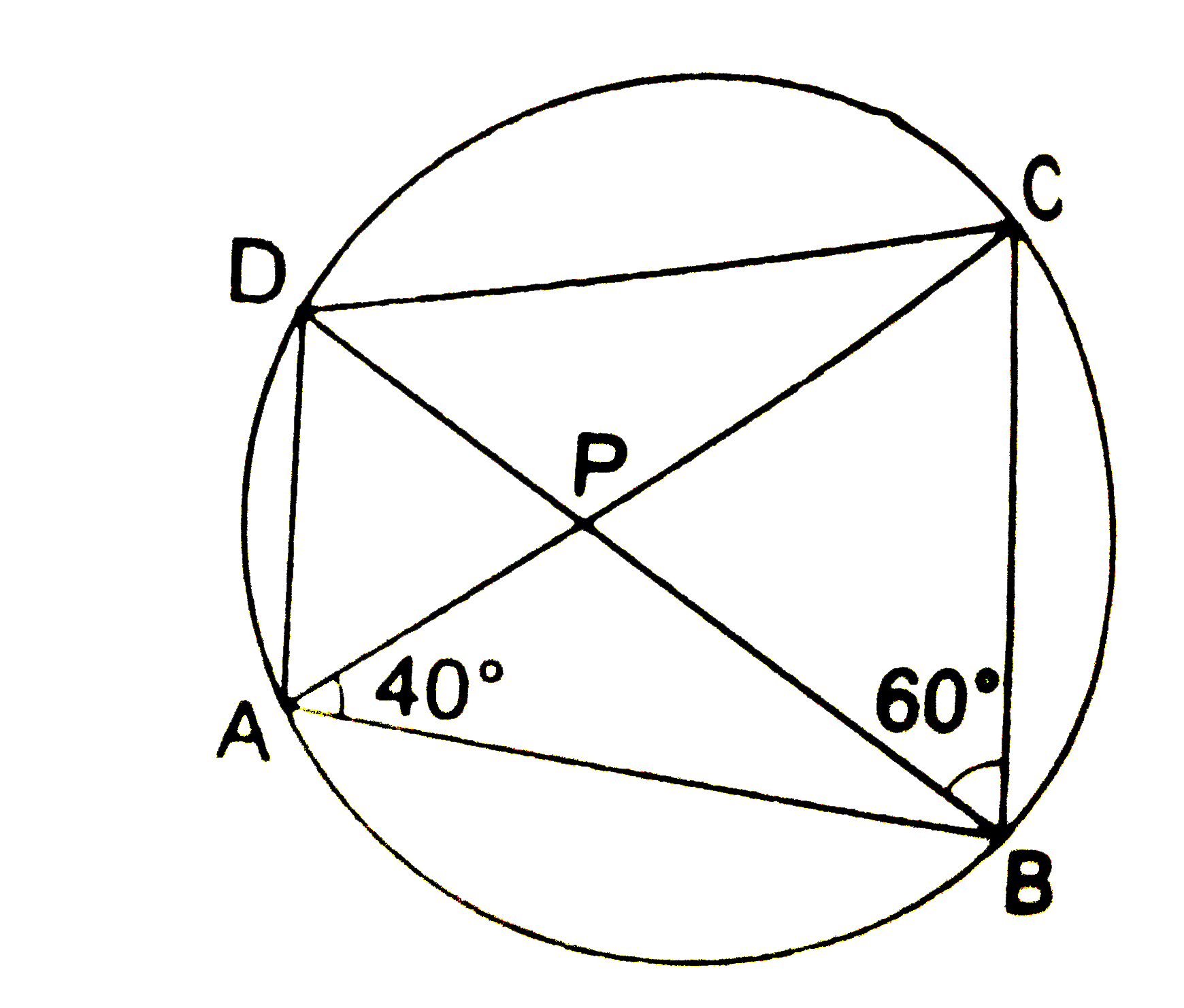
In the given figure, ABCD is a cyclic quadrilateral whose diagonals intersect at P such that `/_ DBC = 60^(@)` and `/_ BAC = 40^(@)`
Find `(i) /_ BCD , (ii) /_ CAD`
View SolutionIn the given figure , POQ is a diameter and PQRS is a cyclic quadrilateral. If `/_ PSR = 150^(@)`, find `/_ RPQ`

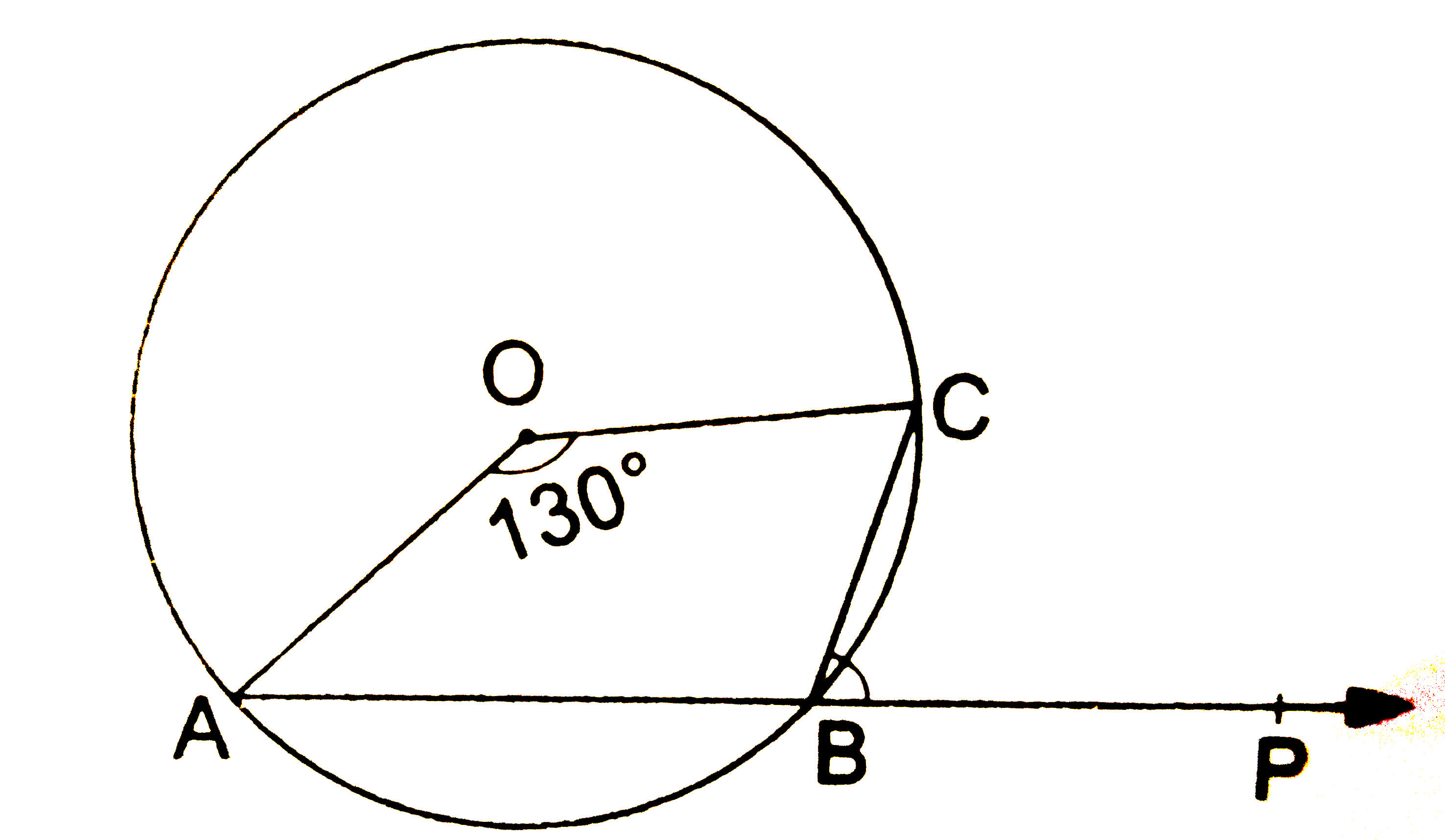
View SolutionIn the given figure, O is the centre of the circle and arc subtends an angle of `130^(@)` at the centre. If AB is extends to P, find `/_ PBC`.
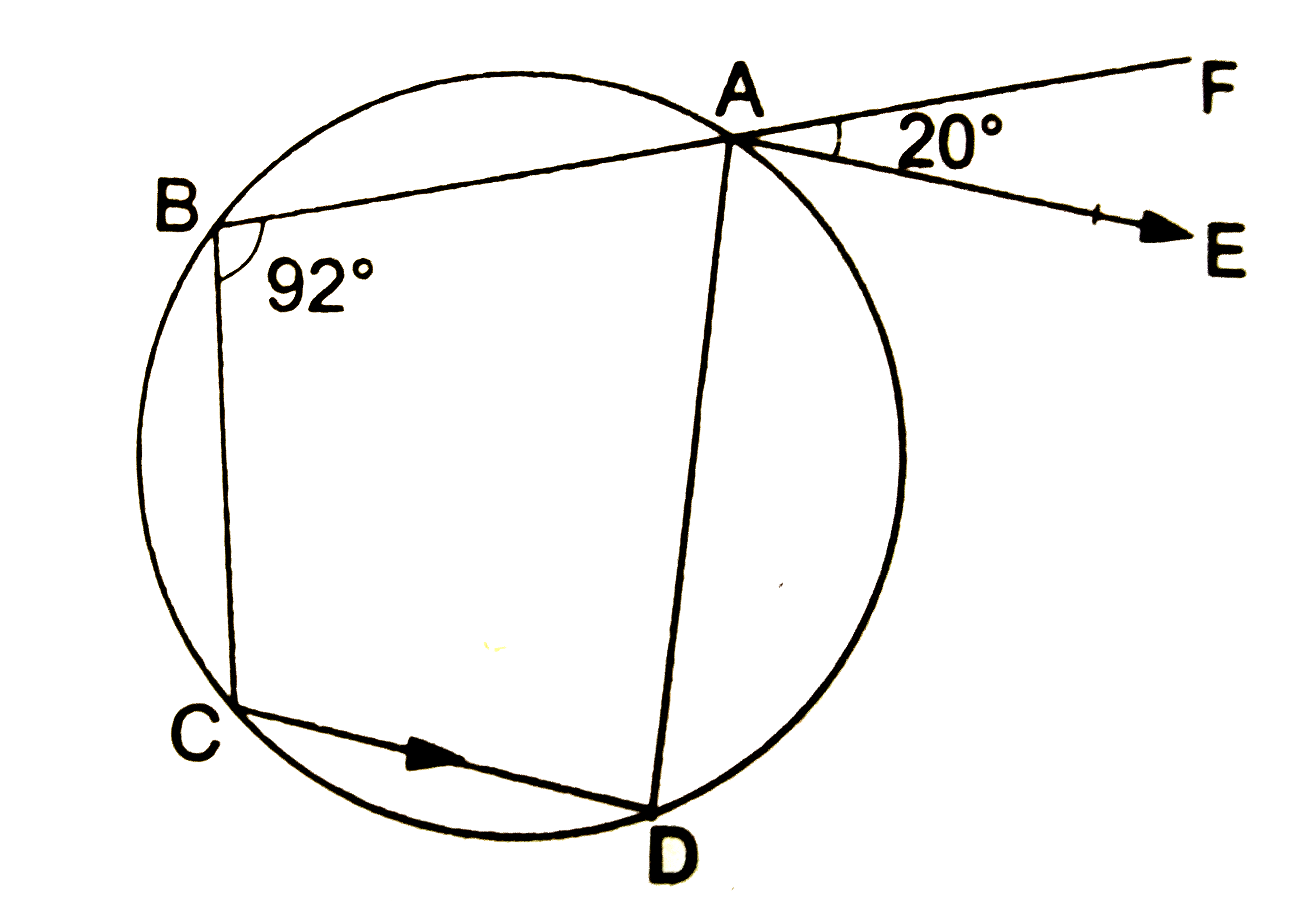
View SolutionIn the given figure , ABCD is a cyclic quadrilateral in which AE is drawn parallel to CD, and BA is produed to F.If `/_ ABC = 92^(@)` and `/_ FAE = 20^(@)` , find `/_ BCD`.
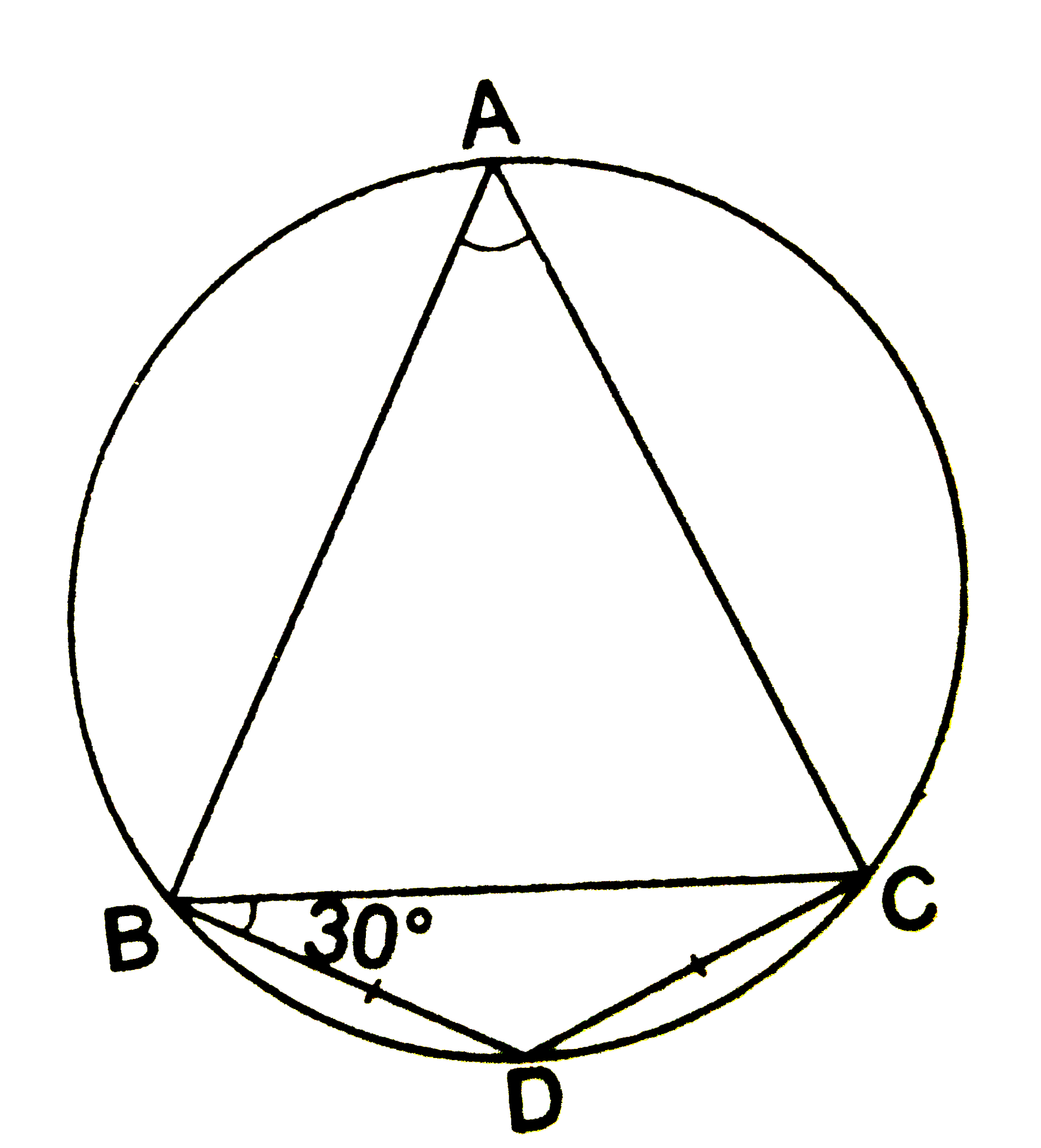
View SolutionIn the given figure, `BD = DC` and `/_ CBD = 30^(@)`, find `/_ BAC`.
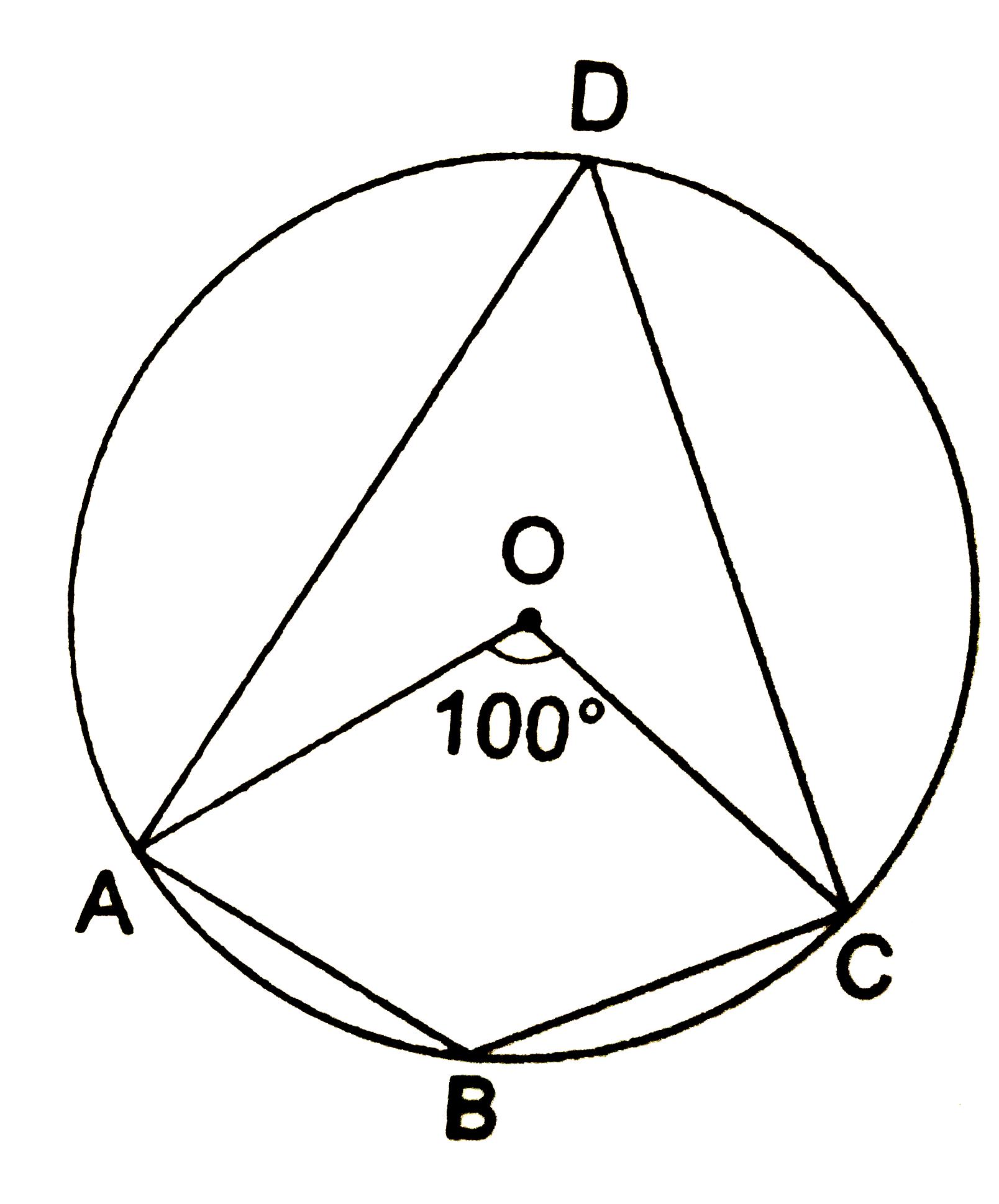
View SolutionIn the given figure, O is the centre of the given circle and measure of arc ABC is `100^(@)`. Determine `/_ ADC` and `/_ ABC`.
View SolutionIn the given figure, , `Delta ABC` is equilateral . Find `(i) /_ BDC , (ii) /_ BEC.`

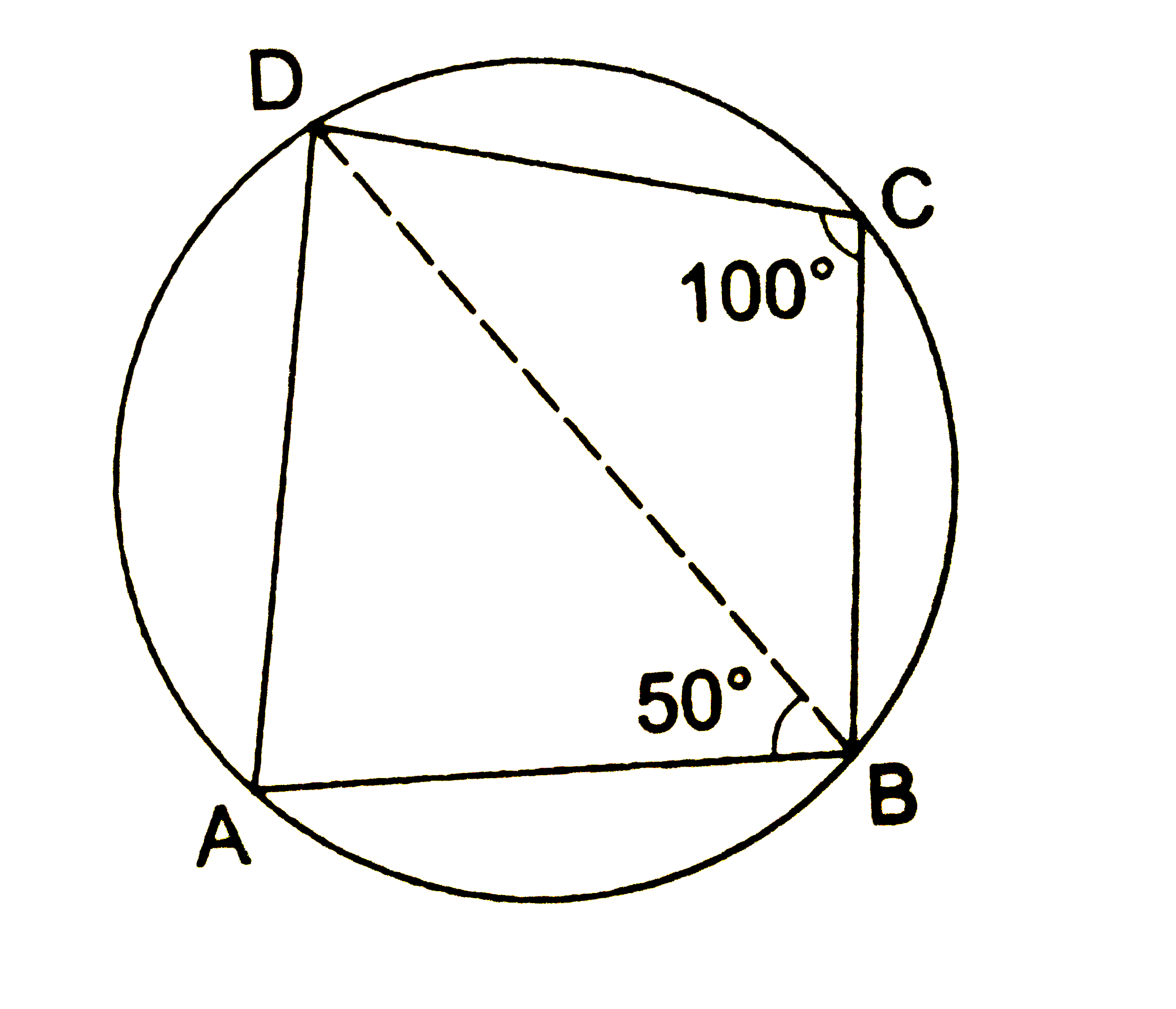
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral in which `/_ BCD= 100^(@) ` and `/_ ABD = 50^(@)` . Find `/_ ADB`
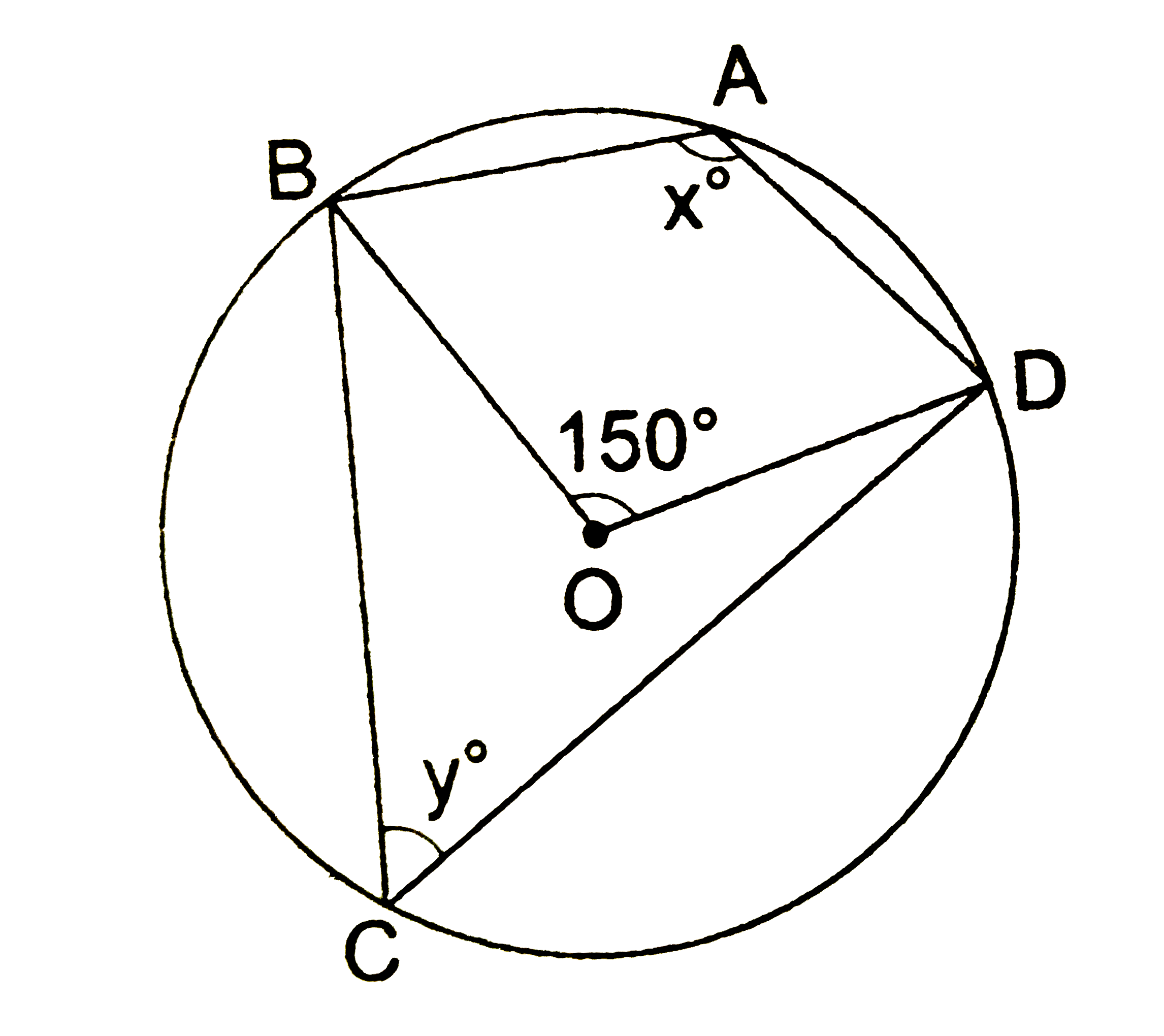
View SolutionIn the given figure, O is the centre of a circle and `/_ BOD = 150^(@)` . Find the values of x and y.
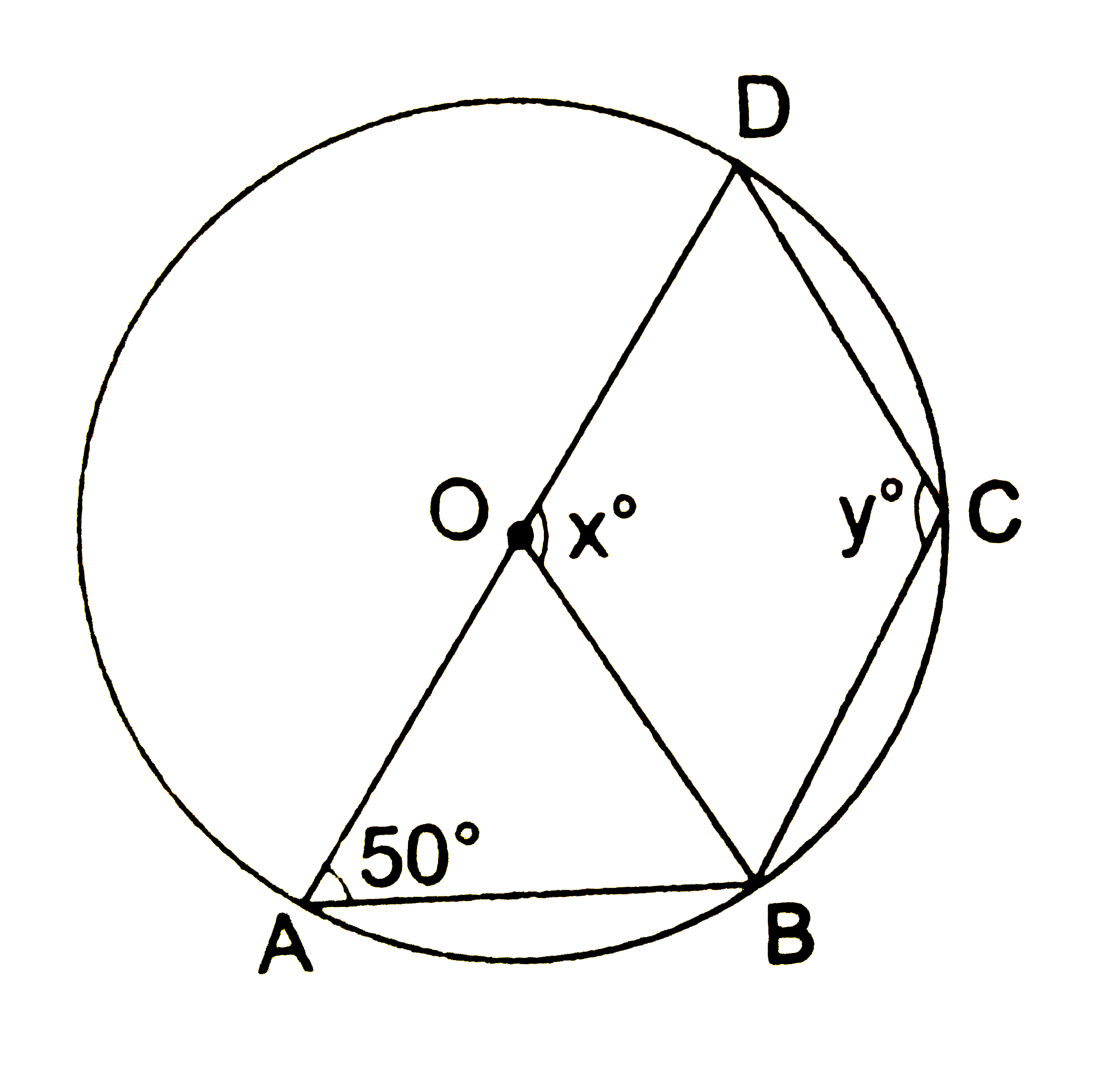
View SolutionIn the given figure , O is the centre of the circle and `/_ DAB = 50^(@)` . Calculate the values of x and y .
View SolutionIn the given figure, sides AD and AB of cyclic quadrilateral ABCD are produced to E and F respectively.
If `/_ CBF = 130^(@)` and `/_ CDE = x^(@)`, find the value of x .

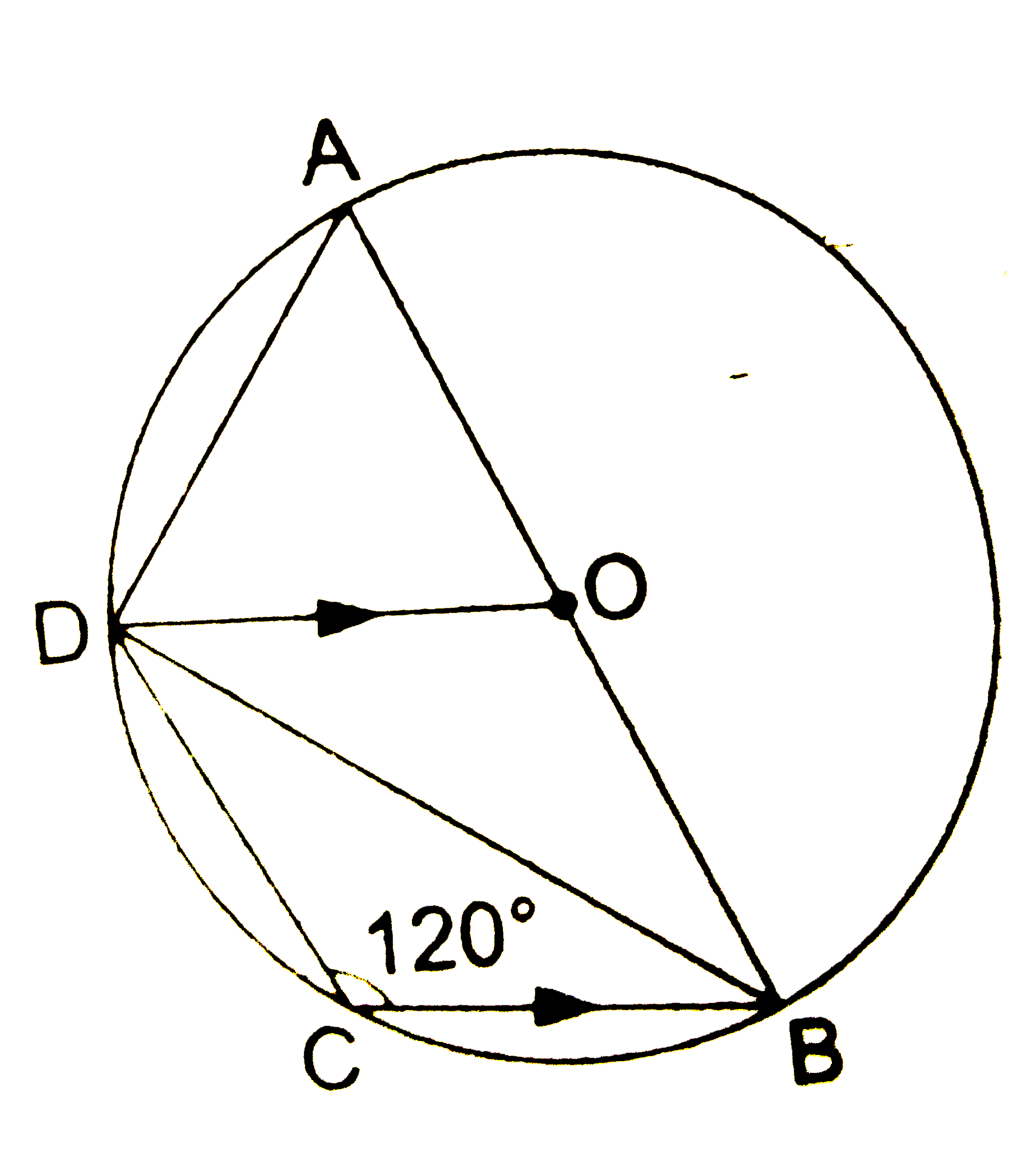
View SolutionIn the given figure, AB is a diameter of a circle with centre O and `DO || CB`.
In `/_ BCD = 120^(@)`, calculate
`(i) /_ BAD` , (ii) `/_ ABD`
(iii) `/_ CBD`, (iv) `/_ ADC`
Also, show that `Delta AOD` is an equilateral triangle.
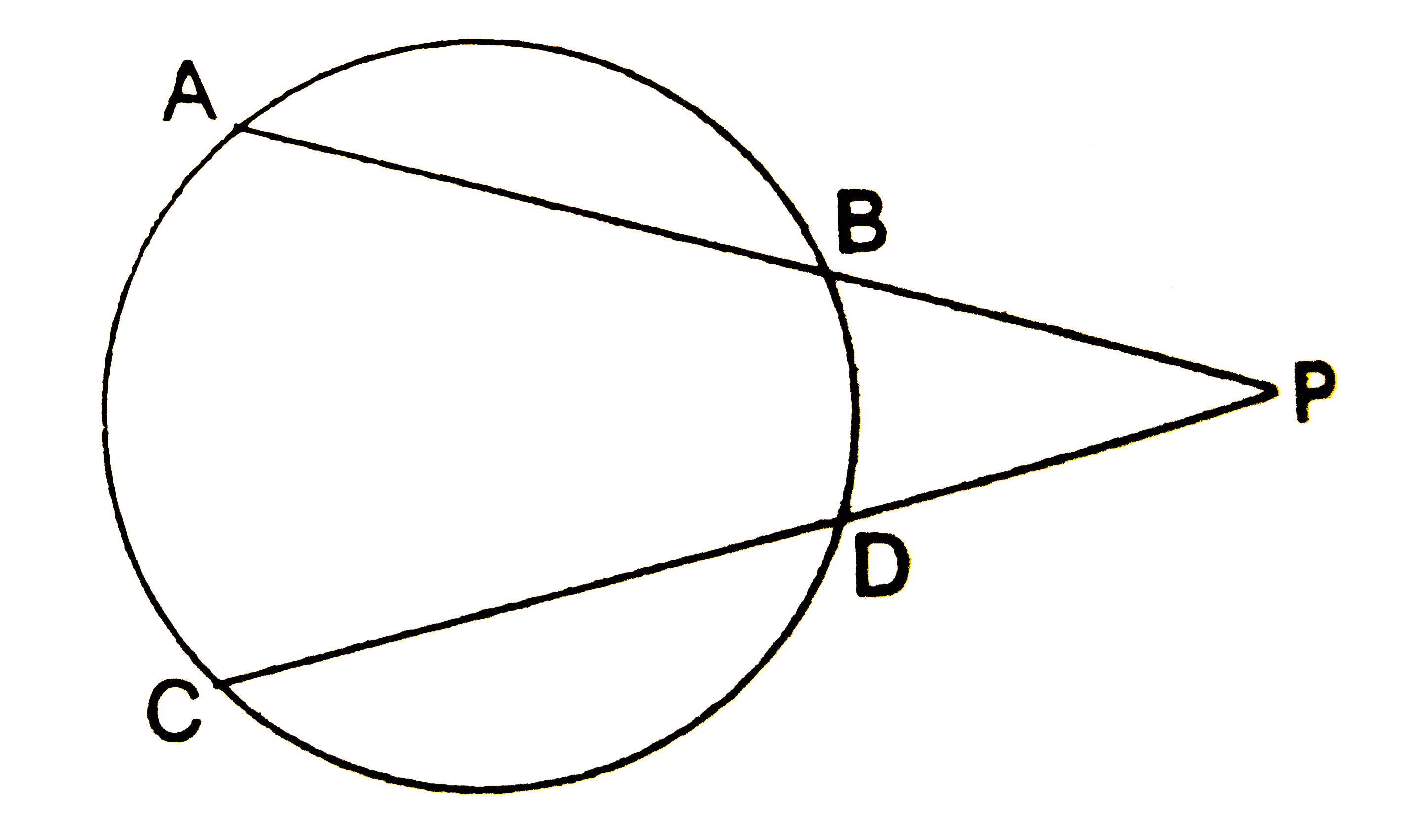
View SolutionTwo chords AB and CD of a circle intersect each other at P outside the circle. If `AB =6cm, BP = 2 cm` and `PD = 2.5cm` , find CD.
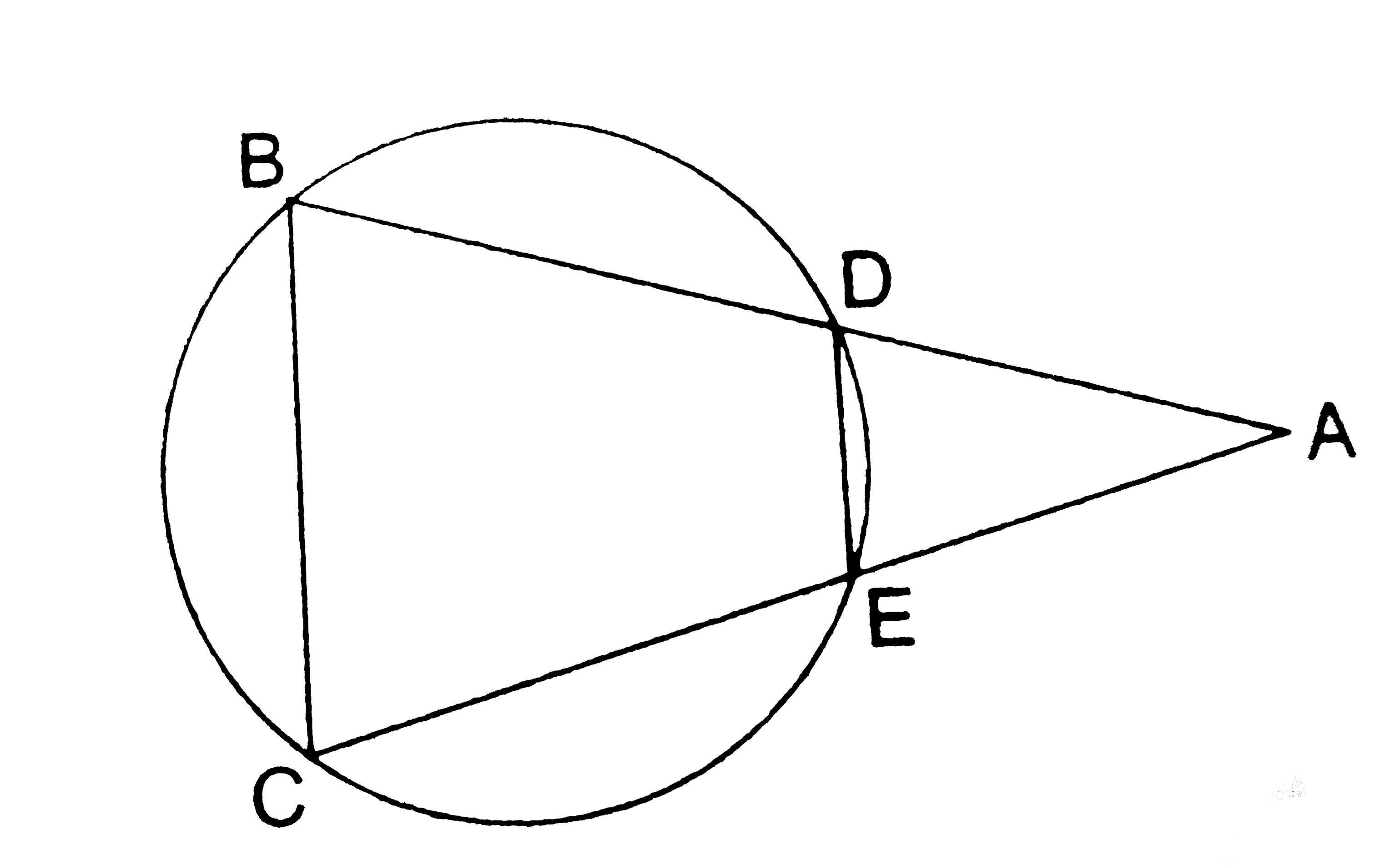
View SolutionIn the given figure, O is the centre of a circle. IF `/_ AOD = 140^(@)` and `/_ CAB = 50^(@)`, calculate.
`(I) /_ EDB , (ii) /_ FBD`.

View SolutionIn the given figure, `Delta ABC` is an isosceles triangle in which `AB = AC` and a circle passing through B and C intersects AB and AC at D and E respectively. Prove that `DE||BC`
View SolutionIn the given figure, AB and CD are two parallel chrods of a circle. If BDE and ACE are straight lines, intersecting at E, prove that `Delta AEB` is isosceles.

View SolutionIn the given figure, `/_ BAD = 75^(@), /_ DCF = x^(@)` and `/_ DEF = y^(@)` .
Find the values of x and y .
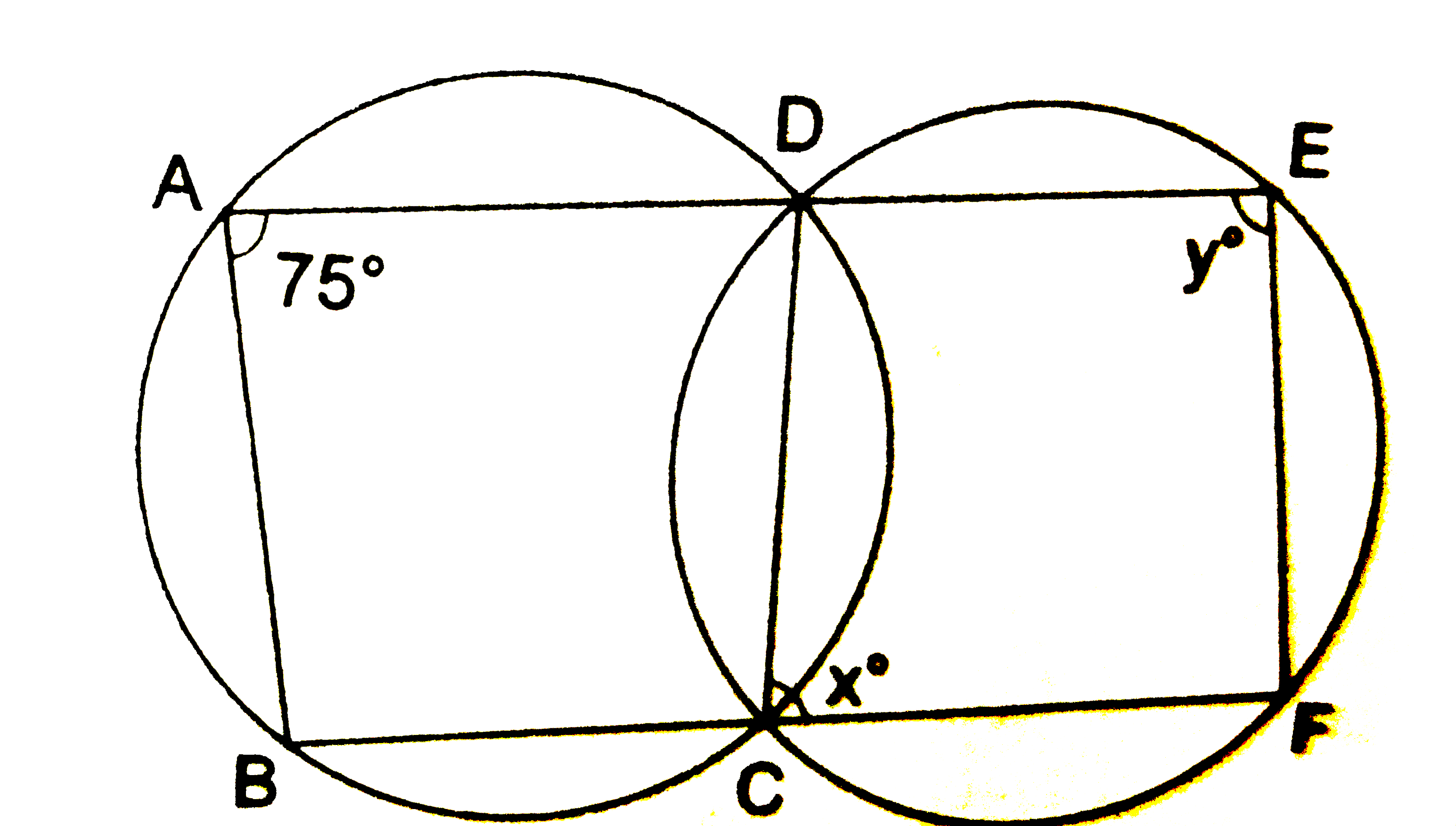
View SolutionIn the given figure, ABCD is a quadrilateral in which AD`=` BC and `/_ ADC = /_ BCD`. Show that the points A,B,C,D lie on a circle.

View SolutionProve that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
View SolutionProve that the circle drawn with any side of a rhombus as a diameter, posses through the point of intersection of its diagonals.
View SolutionProve that the centre of the circle circumscribing the cyclic rectangle `A B C D` is the point of intersection of its diagonals.
View SolutionGive a geometrical construction for finding the fourth point lyingon a circle passing through three given points, without finding the centre of the circle. Justify the construction.
View SolutionIn a cyclic quadrilateral `A B C D ,` if `/_A-\ /_C=60^0,` prove that the smaller of two is `60^0`
View SolutionThe diagonals of a cyclic quadrilateral are at right angles. Prove tha the perpendicular from the point of their intersection on any side when produced backwards , bisects the opposite side.
View SolutionOn a common hypotenuse AB, two right angled triangles, ACB and ADB are situated on opposite sides. Prove that `angleBAC=angleBDC`.
View Solution`ABCD` is such a quadrilateral that A is the centre of the circle passing through `B, C and D`. Prove that `/_CBD+ /_CDB =1/2 /_BAD`.
View Solution
EXERCISE 12C questions and complete solutions for chapter CIRCLES of RS AGGARWAL MATHS (HINGLISH) of Class 9