Level 3 from ARIHANT PHYSICS (HINGLISH) FIRST LAW OF THERMODYNAMICS for Class 11
| Class 11 | PHYSICS |
| Chapter | FIRST LAW OF THERMODYNAMICS |
| ARIHANT PHYSICS (HINGLISH) | Level 3 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 2
Which of the words-out of reversible, irreversible, adiabatic, isothermal, isochoric and isobaric-will you choose to describe the following processes–
(i) A bullet stops in a target [system is bullet plus target].
(ii) A gas, enclosed in a metallic cylinder provided with a piston, is slowly expanded [System is gas]. There is friction between piston and cylinder.
(iii) A piece of hot stone (which has coefficient of thermal expansion equal to zero) is dipped into cold water [System is stone]. View SolutionQuestion 3
Calculate the amount of heat required in calorie to change 1 g of ice at −10∘C to steam at 120∘C. The entire process is carried out at atmospheric pressure. Specific heat of ice and water are 0.5calg−1.∘C−1 and 1.0calg−1.∘C−1 respectively. Latent heat of fusion of ice and vaporization of water are 80calg−1 and 540calg−1 respectively. Assume steam to be an ideal gas with its molecules having 6 degrees of freedom. Gas constant R=2calmol−1K−1. View SolutionQuestion 8
(i) A horizontal cylinder is fitted with a smooth movable piston. The cylinder contains an ideal gas. The gas is heated slowly so that the piston gradually moves out. After moving out for some distance the piston encounters an ideal spring and compresses it while moving out. Draw P – V diagram for the entire process.
(ii) One mole of an ideal gas is expanded isothermally at temperature T0 to double its volume from V0 to 2V0. Draw a graph showing the variation of volume (V) of the gas versus the amount of heat (Q) added to it. View SolutionQuestion 9
A spherical balloon contains air at pressure P1 and is placed in vacuum. It has an initial diameter of D1. The balloon is heated until its diameter becomes D2=2D1. It is known that pressure in the balloon is proportional to its diameter. Calculate the work done by the gas in expansion.View SolutionQuestion 10
(i) An adiabatic cylinder contains an ideal gas. It is fitted with a freely movable insulating piston. In one experiment the piston is pulled out very fast to double the volume of the gas. In another experiment starting from same initial state, the piston is pulled out very slowly to double the volume of the gas. At the end of which experiment the final pressure of the gas will be higher?
(ii) An ideal gas is contained in a cylinder fitted with a movable piston. In an experiment ‘A’ the gas is allowed to perform a work W(>0) on the surrounding during an isobaric process and thereafter the pressure of the gas is reduced isochorically to half the initial value. At the end of the experiment the temperature of the gas is TA. In a different experiment ‘B’ the pressure of the gas is reduced to half in an isochoric process and then the gas performs a work W on the surrounding during an isobaric process. At the end of the experiment the gas temperature is TB. Which is higher, TA or TB?View SolutionQuestion 12
Two thermally insulated vessels are filled with an ideal gas. The pressure, volume and temperature in the two vessels are P1,V1,T1 and P2,V2,T2 respectively. Now, the two vessels are connected using a short insulating tube.
(a) Find final temperature of the gas.
(b) Express the final pressure of the gas in terms of P1,V1,P2 and V2 only.View SolutionQuestion 13
Two tanks are connected by a valve. One tank contains 2 kg of an ideal gas at 77∘C and 0.7 atm pressure. The other tank has 8kg of same gas at 27∘C and 1.2 atm pressure. The valve is opened and the gases are allowed to mix. The final equilibrium temperature was found to be 42∘C.
(a) Find the equilibrium pressure in both tanks.
(b) How much heat was transferred from surrounding to the tanks during the mixing process. Given: Cv for the gas is 0.745KJkg−1K−1. View SolutionQuestion 15
A sample of an ideal gas has diatomic molecules at a temperature at which effective degree of freedom is 5. Under the action of a suitable radiation the molecules split into two atoms. The ratio of the number of dissociated molecules to the total number of molecules is a. Plot the ratio of molar specific heats γ(=CpCv) as a function of α.View SolutionQuestion 16
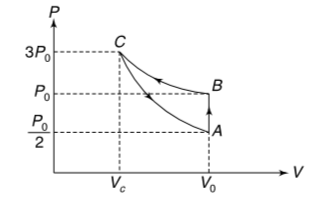
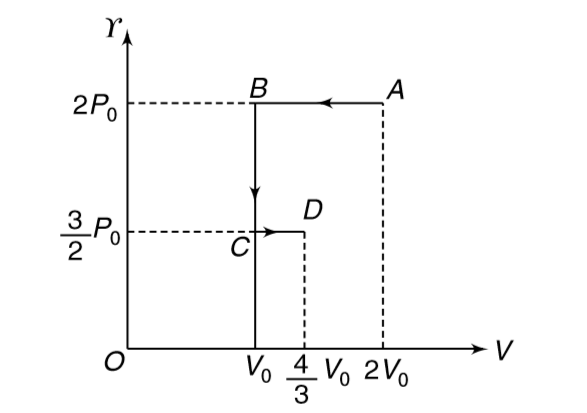
An ideal gas undergoes a series of processes represented bya→B→C→D on the P-V diagram. Answer the following questions.
(a) Is the internal energy of the gas at B and D equal?
(b) Find work done by the gas in the process A rarr B rarr C rarr D.
(c) Is it right to say that point B and D lie on an isotherm?
(d) Find the ratio of internal energy of the gas in state A to that in state D.
 View Solution
View SolutionQuestion 17
30 people gather in a 10m×5m×3m room for a confidential meeting. The room is completely sealed off and insulated. Calculate the rise in temperature of the room in half an hour. Assume that average energy thrown off by the body of a person is 2500 kcal/day, density of air is 1.2kgm3 and specific heat specify capacity of air at constant volume is 0.24kcalkg−1.∘C−1. Neglect volume occupied by human bodies. View SolutionQuestion 19
An ideal mono atomic gas A is supplied heat so as to expand without changing its temperature. In another process, starting with the same state, it is supplied heat at constant pressure. In both the cases a graph of work done by the gas (W) is plotted versus heat added (Q) to the gas. The ratio of slope of the graphs obtained in first and second process is η1. The same ratio obtained for an ideal diatomic gas in η2. Find the ratio η1η2.View SolutionQuestion 22
A gas undergoes a cyclic process a-b-c-a which is as shown in the PV diagram. The process a-b is isothermal, b-c is adiabatic and c-a is a straight line on P-V diagram. Work done in process ab and bc is 5 J and 4 J respectively. Calculate the efficiency of the cycle, if the area enclosed by the diagram abca in the figure is 3 J.
 View Solution
View SolutionQuestion 24
A mass less piston divides a thermally insulated cylinder into two parts having volumes V = 2.5 litre and 3 V = 7.5 litre. 0.1 mole of an ideal gas is confined into the part with volume V at a pressure of P=105N/m2. The other part of the cylinder is empty. The piston is now released and the gas expands to occupy the entire volume of the cylinder. Now the piston is pressed back to its initial position. Find final temperature of the gas.
[Take R=253Jmol−1K−1 and γ=1.5 for the gas]View SolutionQuestion 27
Air is contained in a vertical piston – cylinder assembly fitted with an electric heater. The piston has a mass of 50 kg and cross sectional area of 0.1m2. Mass of the air inside the cylinder is 0.3 kg. The heater is switched on and the volume of the air slowly increases by 0.045m3. It was found that the internal energy of the air increased by 32.2kJ/kg and that of the piston increased by 0.06 kJ/kg. Assume that the container walls and outer surface of the piston are well insulated and there is no friction. The atmospheric pressure is 100 kPa. Determine the heat transferred by the heater to the system consisting of air and the piston.
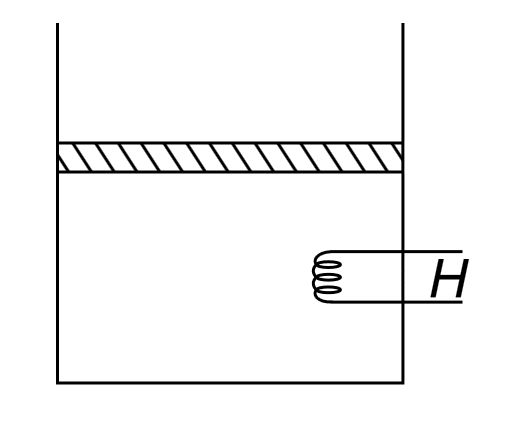 View Solution
View SolutionQuestion 28
One mole of an ideal mono atomic gas is at a temperature T0=1000K and its pressure is P0. The gas is adiabatically cooled so that its pressure becomes 23P0. Thereafter, the gas is cooled at constant volume to reduce its pressure to P03 . Calculate the total heat absorbed by the gas during the process.
Take R=253Jmol−1K−1 and (23)2/5=0.85 View SolutionQuestion 31
A container has a tight fitting movable piston which can slide without friction. The compartment containing spring has vacuum and to the left of the piston there is diatomic gas. If vacuum is created in the right compartment also the piston touches the right wall and the spring is relaxed. Find the heat capacity of the system neglecting the heat capacities of the material of spring, container and the piston. Express your answer in terms of P0,V0 and T0.
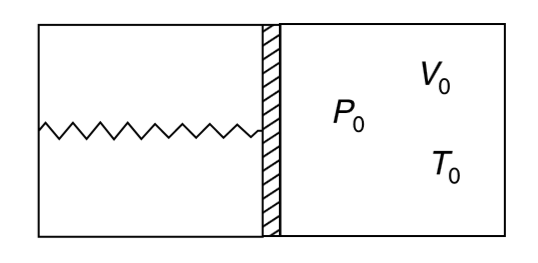 View Solution
View SolutionQuestion 32
One mole of a gas is in state A[P,V,TA]. A small adiabatic process causes the state of the gas to change to B[P+dP,V+dV,TB]. The changes dV & dP are infinitesimally small and dV is negative. An alternative process takes the gas from state A to B via A→C→B. A→C is isochoric and C→B is isobaric path. State at C is [P+dP,V,TC].
(a) Rank the temperatures TA,TB and TC from highest to lowest.
(b) Find g of the gas in terms of TA, TB and TC.
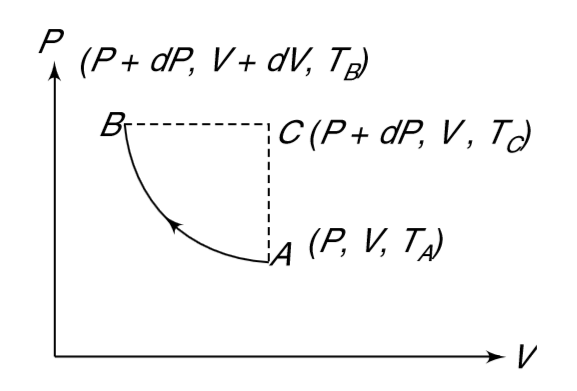 View Solution
View SolutionQuestion 33
A metal cylinder of density d, cross sectional area A and height h is standing on a horizontal surface. Coefficient of linear expansion of the metal is apha.∘C−1 and its specific heat capacity is S. Calculate the rise in temperature of the cylinder if a heat ΔQ is supplied to it. Assume no atmosphere. View SolutionQuestion 34
n moles of an ideal mono atomic gas is initially at pressure 32P0 and volume V0. Its volume is doubled by an isobaric process. After this the gas is adiabatically expanded so as to make its volume 16V0. Now the gas is isobarically expanded. Finally, the gas is made to return to its initial state by an isothermal process.
(a) Represent the process on a P–V diagram.
(b) Calculate work done by the gas in one cycle. View SolutionQuestion 35
One end of an insulating U tube is sealed using insulating material. A mono atomic gas at temperature 300 K occupies 20 cm length of the tube as shown. The level of mercury on two sides of the tube differ by 5 cm. The other end of the tube is open to atmosphere. Area of cross section of the tube is uniform and is equal to 0.01m2. The gas in the tube is heated by an electric heater so as to raise its temperature to 562.5 K. Assume that no heat is conducted to mercury by the gas.
(a) Find the final length of the gas column.
(b) Find the amount of heat supplied by the heater to the gas.
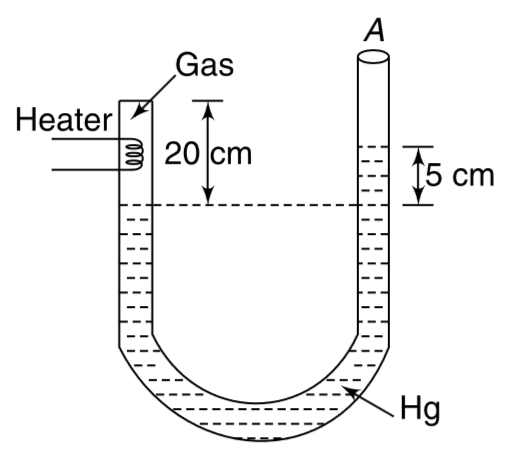 View Solution
View SolutionQuestion 36
Air is filled inside a jar which has a pressure gauge connected to it. The temperature of the air inside the jar is same as outside temperature (=T0) but pressure (P1) is slightly larger than the atmospheric pressure (P0). The stopcock is quickly opened and quickly closed, so that the pressure inside the jar becomes equal to the atmospheric pressure P0. The jar is now allowed to slowly warm up to its original temperature T0. At this time the pressure of the air inside is P2(P0<P2<P1). Assume air to be an ideal gas. Calculate the ratio of specific heats (=γ) for the air, in terms of P0,P1 and P2.
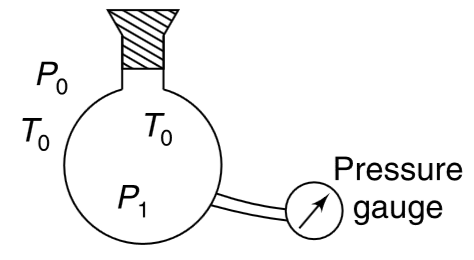 View Solution
View SolutionQuestion 39
A gas-gun has a cylindrical bore made in an insulating material. Length of the bore is L. A small bullet having mass m just fits inside the bore and can move frictionlessly inside it. Initially n moles of helium gas is filled in the bore to a length L0. The bullet does not allow the gas to leak and the bullet itself is kept at rest by a stopper S. The gas is at temperature T0. The gun fires if the stopper S is removed suddenly. Neglect atmospheric pressure in your calculations [Think that the gun is in space].
(a) Calculate the speed with which the bullet is ejected from the gun.
(b) Find the maximum possible speed that can be imparted to the bullet by using n moles of helium at temperature T0.
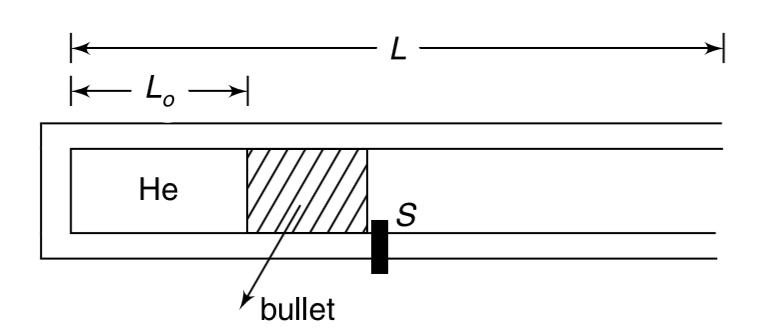 View Solution
View SolutionQuestion 40
During a process carried on an ideal gas it was found that η(<1) times the heat supplied to the gas is equal to increase in internal energy of the gas. Write the process equation in terms of pressure (P) and volume (V) of the gas. It is given that ratio of specific heats for the gas is CPCV=γ.View SolutionQuestion 41
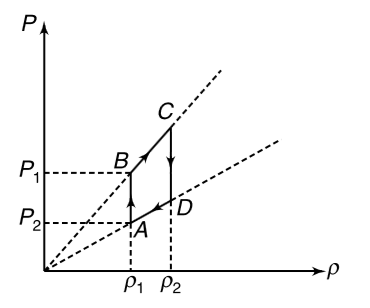
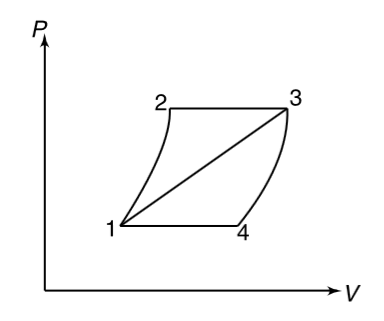
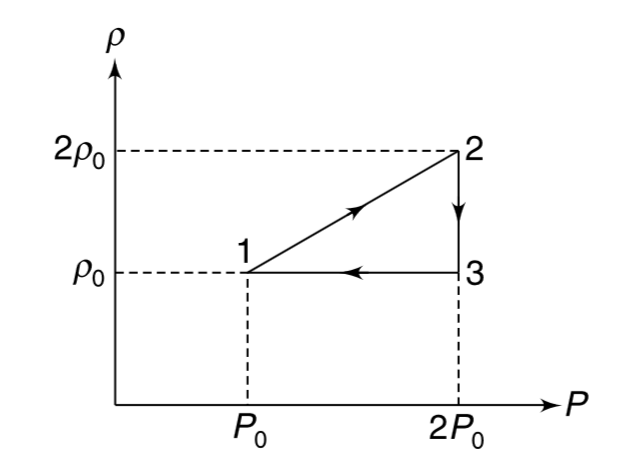
An ideal gas is taken through a thermodynamic cycle ABCDA. In state A pressure and volume are P0 and V0 respectively. During the process A→B, work done by the gas is zero and its temperature increases two fold. During the process B→C, internal energy of the gas remains constant but work done by it is WBC=–P0V0ln2. In the process C→D, the temperature decreases by 50% while the volume does not change. In the process D→A the temperature of the gas does not change.
(a) Draw pressure – volume (P–V) and pressure – density (P–ρ) graph for the cyclic process.
(b) Calculate work done on the gas during the cycle. View SolutionQuestion 42
(i) A conducting piston divides a closed thermally insulated cylinder into two equal parts. The piston can slide inside the cylinder without friction. The two parts of the cylinder contain equal number of moles of an ideal gas at temperature T0. An external agent slowly moves the piston so as to increase the volume of one part and decrease that of the other. Write the gas temperature as a function of ratio (β) of the volumes of the larger and the smaller parts. The adiabatic exponent of the gas is γ.
(ii) In a closed container of volume V there is a mixture of oxygen and helium gases. The total mass of gas in the container is m gram. When Q amount of heat is added to the gas mixture its temperature rises by ΔT. Calculate change in pressure of the gas. View SolutionQuestion 43
A spherical container made of non conducting wall has a small orifice in it. Initially air is filled in it at atmospheric pressure (P0) and atmospheric temperature (T0). Using a small heater, heat is slowly supplied to the air inside the container at a constant rate of H J/s. Assuming air to be an ideal diatomic gas find its temperature as a function of time inside the container.
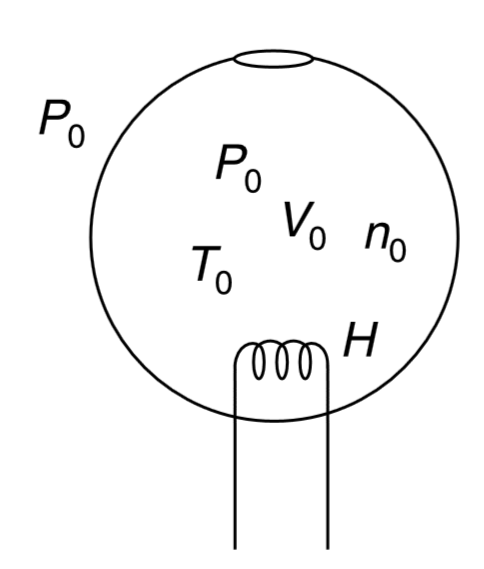 View Solution
View SolutionQuestion 44
A glass tube is inverted and dipped in mercury as shown. One mole of an ideal monoatomic gas is trapped in the tube and the tube is held so that length of the tube above the mercury level is always h0 meter. The atmospheric pressure is equal to h0 meter of mercury. The mercury vapour pressure, heat capacity of mercury, tube and the container are negligible. How much heat must be supplied to the gas inside the tube so as to increase its temperature by ΔT?
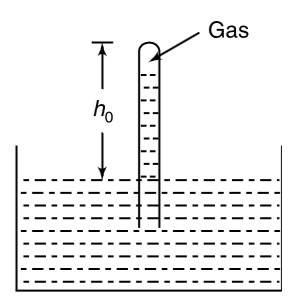 View Solution
View SolutionQuestion 45
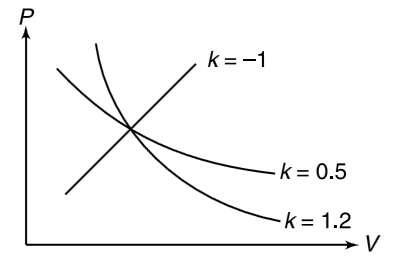
Figure shows P versus V graph for various processes performed by an ideal gas. All the processes are polytropic following the process equation PVk= constant.
(i) Find the value of k for which the molar specific heat of the gas for the process is CP+CV2. Does any of the graph given in figure represent this process?
(ii) Find the value of k for which the molar specific heat of the gas is CV+CP. Assume that gas is mono atomic. Draw approximately the P versus V graph for this process in the graph given above.
 View Solution
View SolutionQuestion 47
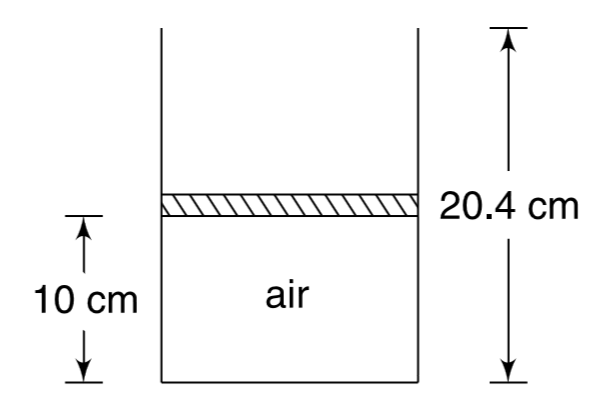
In the arrangement shown in figure, the piston can smoothly move inside the cylinder. The mass of the piston is m = 100 g and its cross sectional area is A=10cm2. The length of air column at temperature of T=27∘C is 10 cm. Overall length of the cylinder is 20.4 cm. The container is turned upside down and the length of the air column in equilibrium was found to be l at 27∘C. Take R=253Jmol−1K−1 and assume air to be diatomic gas. g=10m/s2, atmospheric pressure is 1.01×105Nm2
(a) Find l
(b) If the air in the container is supplied heat in upside down position, the piston slowly begins to move down, and ultimately it gets ejected out of the cylinder. Calculate the amount of heat that the air must absorb for the piston to come out.
 View Solution
View SolutionQuestion 48
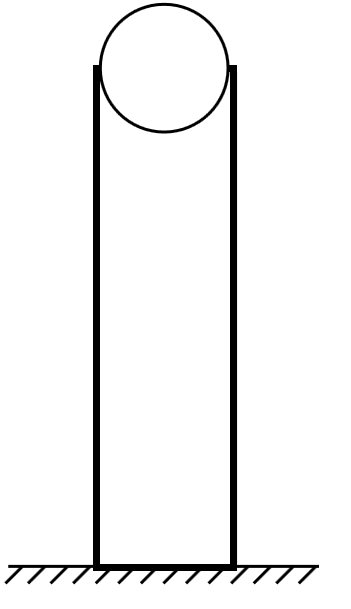
There is a long vertical tube of radius r containing air at atmospheric pressure. A steel ball is held at the mouth of the tube and dropped. The ball has radius r and it just fits inside the tube. The tube wall is perfectly smooth and no air can leak from the tube as the ball falls inside it. The ball falls through half the length of the tube before coming to rest. Assume that wall of the tube is perfectly conducting and temperature of the air inside the tube remains constant. Density of steel is d and atmospheric pressure is P0 and take L>>r. Take air to be an ideal gas.
(a) Find the radius (r) of the tube.
(b) At what depth from the top of the tube the ball will be in equilibrium?
 View Solution
View SolutionQuestion 49
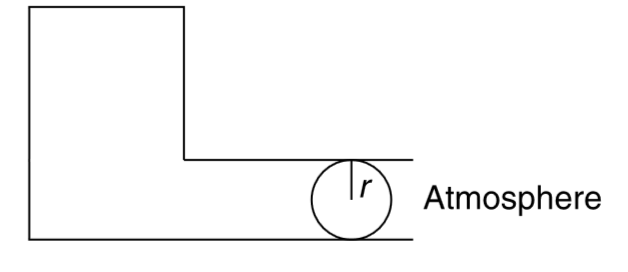
A ball of radius r fits tightly inside a tube attached to a container. There is no friction between the tube wall and the ball. Volume of air inside the container is V0 when the ball is in equilibrium. Density of the material of the ball is d and atmospheric pressure is P0. If the ball is displaced a little from its equilibrium position and released, find time period of its oscillation. Assume that temperature in the container remains constant and that air is an ideal gas.
 View Solution
View SolutionQuestion 50
An ideal mono atomic gas is at temperature T0. The pressure and volume are quasi-statically doubled such that the process traces a straight line on the PV diagram.
(a) Calculate the heat absorbed by the gas in the process if number of moles of the gas in the sample is n.
(b) Calculate the average molar specific heat capacity of the gas for the process. View SolutionQuestion 51
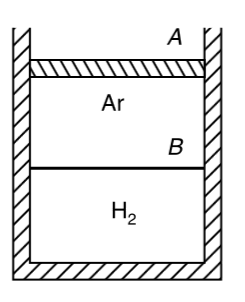
A cylinder contains equal volumes of Ar and H2, separated by a freely movable piston B. Piston A can also move without friction. Volume of each gas in equilibrium isV0. All walls of the container including piston A are non conducting.
(i) Piston A is pushed down slowly till the volume occupied by argon becomes V04 . Find the volume of H2. Assume that piston B is also non conducting.
(ii) Now assume that piston B is conducting and assume that each gas has n moles. The external agent performs work W0 in slowly pushing down the piston A. Find rise in temperature of each gas.
 View Solution
View SolutionQuestion 53
A heat engine is based on a gaseous cycle comprising of four processes viz. isothermal expansion at temperature (T1), isochoric cooling to temperature T2, isothermal compression (at T2) and isochoric heating back to temperature T1. The engine has been designed so as to completely use the heat rejected during isochoric cooling, in the isochoric heating process. Calculate the efficiency of this reversible cycle. Show the process on a PV graph. View SolutionQuestion 54
An ideal gas with a known γ, completes a cycle consisting of two isotherms and two isobars. The isothermal processes are executed at temperatures T and T'(<T) and isobaric processes are completed at pressures P0 and eP0 [e = base of natural logarithm]. Find the efficiency of the cycle. View SolutionQuestion 56
Helum gas is used as working substance in an engine working on a thermodynamic cycle A – B – C – D – A. Process AB is isobaric, BC is adiabatic compression. During process CD, pressure is increased keeping the volume constant and DA is an isothermal process. The gas has maximum volume at A and the ratio of maximum to minimum volume during the entire cycle is 8√2 . Also, the ratio of maximum to minimum absolute temperature is 4.
(a) Represent the cycle on a P – V diagram.
(b) Calculate efficiency of the cycle in percentage if it is used as an engine. [Take ln 2 = 0.693] View SolutionQuestion 57
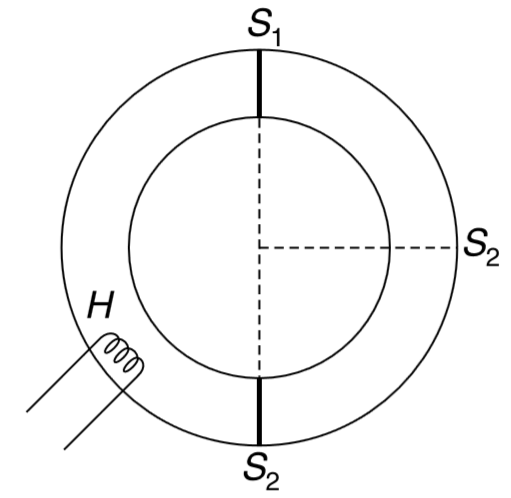
A ring shaped tube has uniform cross sectional area and its entire volume is 2V0. The tube is well insulated from the surrounding. Inside the tube there is an adiabatic fixed wall S1 and another movable adiabatic partition S2. Initially, the movable partition is diametrically opposite to S1 and the two halves of the tube have equal amount of an ideal gas (g = 1.5) at same pressure P0. Now, a heater H is switched on which supplies heat slowly to one of the chambers. Heater is kept on till the partition S2 moves through the quarter of the circle. At this position the heater is switched off and the partition S2 remains in equilibrium. Neglect any friction as well as heat loss to the surrounding through the walls of the tube. Find the heat supplied by the heater to the gas.
 View Solution
View SolutionQuestion 58
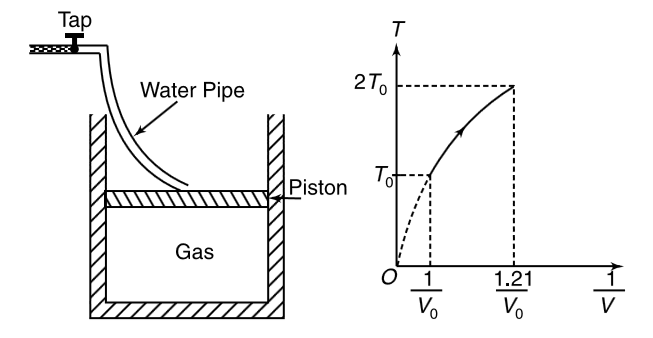
A cylindrical container has insulating wall and an insulating piston which can freely move up and down without any friction. It contains a mixture of ideal gases. Originally the gas is at atmospheric pressure P0 and temperature (T0). A tap positioned above the container is opened and it supplies water at a constant rate of dmdt=0.25kg/s. The water collects above the piston in the container and the gas compresses. The tap is kept open till the temperature of the gas is doubled. During the process the T vs 1V graph for the gas was recorded and found to be a parabola with its vertex at origin as shown in the graph. Area of piston A=1.515×10−3m2 and atmospheric pressure =105N/m2
(a) Find the ratio of Vrms and speed of sound in the gaseous mixture.
(b) For how much time the tap was kept open?
 View Solution
View SolutionQuestion 60
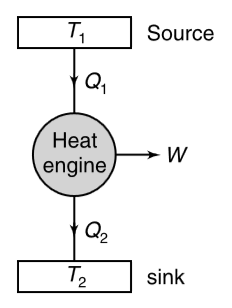
A room air conditioner is a Carnot cycle based heat engine run is reverse. An amount of heat Q2 is absorbed from the room at a temperature T2 into coils having a working gas (these gases are not good for environment!). The gas is compressed adiabatically to the outside temperature T1. Then the gas is compressed isothermally in the unit outside the room, giving off an amount of heat Q1. The gas expands adiabatically back to the temperatureT2 and the cycle is repeated. The electric motor electric consumes power P.
(i) Find the maximum rate at which heat can be removed from the room.
(i) Heat flows into the room at a constant rate of kΔT where k is a constant and ΔT is temperature difference between the outside and inside of the room. Find the smallest possible room temperature in terms of T1,k and P. View SolutionQuestion 61
A Carnot cycle based ideal heat engine operates between two tanks each having same mass m of water. The source tank has an initial temperature of T1=361K and the sink tank has an initial temperature of T2=289K. Assume that the two tanks are isolated from the surrounding and exchange heat with the engine only. Specific heat of water is s.
(a) Find the final common temperature of the two tanks.
(b) Find the total work that the engine will be able to deliver by the time the two tanks reach common temperature.
 View Solution
View SolutionQuestion 62
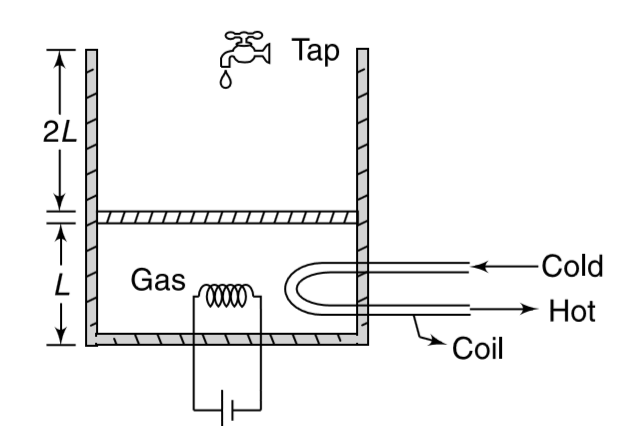
A cylindrical container of height 3L and cross sectional area A is fitted with a smooth movable piston of negligible weight. It contains an ideal diatomic gas. Under normal atmospheric pressure P0 the piston stays in equilibrium at a height L above the base of the container. The gas chamber is provided with a heater and a copper coil through which a cold liquid can be circulated to extract heat from the gas. Volume occupied by the heater and the liquid coil is negligible. Following set of operations are performed to take the gas through a cyclic process.
(1) Heater is switched on. At the same time a tap above the cylinder is opened. Water fills slowly in the container above the piston and it is observed that the piston does not move. Water is allowed to fill the container so that the height of water column becomes L. Now the tap is closed.
(2) The heater is kept on and the piston slowly moves up. Heater is switched off at the time water is at brink of overflowing.
(3) Now the cold liquid is allowed to pass through the coil. The liquid extracts heat from the gas. Water is removed from the container so as to keep the position of piston fixed. Entire water is removed and the gas is brought back to atmospheric pressure.
(4) The circulation of cold liquid is continued and the piston slowly falls down to the original height L above the base of the container. Circulation of liquid is stopped. Assume that the container is made of adiabatic wall and density of water is ρ. Force on piston due to impact of falling water may be neglected.
(a) Draw the entire cycle on a P–V graph.
(b) Find the amount of heat supplied by the heater and the amount of heat extracted by the cold liquid from the gas during the complete cycle.
 View Solution
View SolutionQuestion 63
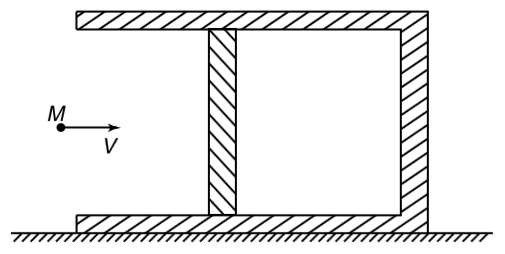
An adiabatic cylindrical chamber with a frictionless movable piston has been placed on a smooth horizontal surface as shown. One mole an ideal monotonic gas is enclosed inside the chamber. Mass of the piston is M and mass of the remaining chamber including the gas is 4 M. The gas is at atmospheric pressure and temperature. A particle of mass M moving horizontally with speed v, strikes the piston elastically. Find the change in temperature of the gas when the compression is maximum.
 View Solution
View SolutionQuestion 64
(a) A polytropic process for an ideal gas is represented by PVx= constant, where x≠1. Show that molar specific heat capacity for such a process is given by C=Cv+R1−x.
(b) An amount Q of heat is added to a mono atomic ideal gas in a process in which the gas performs a work Q2 on its surrounding. Show that the process is polytropic and find the molar heat capacity of the gas in the process.View SolutionQuestion 65
An adiabatic cylinder of cross section A is fitted with a mass less conducting piston of thickness d and thermal conductivity K. Initially, a monatomic gas at temperature T0 and pressure P0 occupies a volume V0 in the cylinder. The atmospheric pressure is P0 and the atmospheric temperature is T1(>T0). Find
(a) the temperature of the gas as a function of time
(b) the height raised by the piston as a function of time.
Neglect friction and heat capacities of the container and the piston. View SolutionQuestion 66
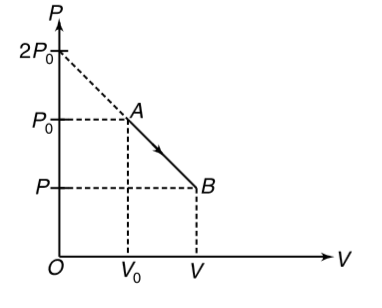
One mole of an ideal gas is expanded from the state A(P0,V0) to final state B having volume V. The process follows a path represented by a straight line on the P–V diagram (see figure). Up to what volume (V) the gas shall be expanded so that final temperature is half the maximum temperature during the process.
 View Solution
View SolutionQuestion 67
An ideal gas, in initial state 1(P1,V1,T1) is cooled to a state 3(P3,V3,T3) by a process which can be represented by a straight one on the P–V graph. The same gas in a different initial state 2 (P2,V2,T1) is cooled to same final state 3 (P3,V3,T3) by a process which can also be represented by a straight line on the same P–V graph. Q1 and Q2 are heat rejected by the gas in the two processes. Which is larger Q1 or Q2. It is given that P_(1) gt P_(2).View SolutionQuestion 68
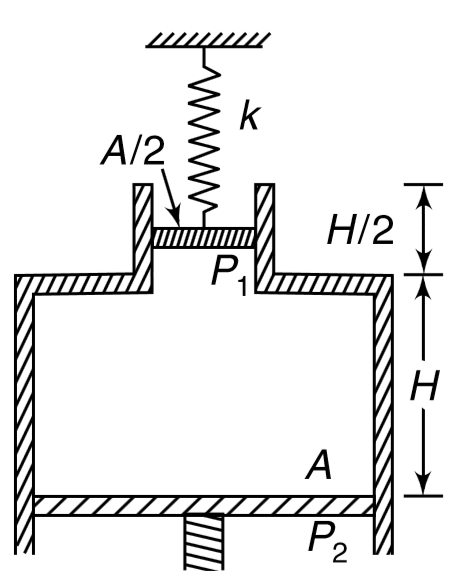
In ideal gas is enclosed in an adiabatic container having cross section A=27cm2 for a part of it and A2 for remaining part. Pistons P1 and P2 can move freely without friction along the inner wall. In the position shown in the figure the spring attached to the piston P1 is relaxed. Sprig constant the spring is K=3700N/m. Piston P2 is pushed up gradually through a distance H2 and its was observed that the piston P1 goes up by 3H32 . Take γ=1.5, mass of piston P1=13.5kg and atmospheric pressure P0=1×105N/m2
(a) Find H.
(b) Find final temperature of the gas if its initial temperature is 300 K.
 View Solution
View SolutionQuestion 69
An insulated cylinder is divided into three parts A, B and C. Pistons 1 and 2 are connected by a rigid rod and can slide without friction inside the cylinder. Piston 1 is perfectly conducting while piston 2 is perfectly insulating. Equal quantity of an ideal gas is filled in three compartments and the state of gas in every part is same (P0V0T0). Adiabatic exponent of the gas is g = 1.5. The compartment B is slowly given heat through a heater H such that the final volume of gas in part C becomes 4V09
(a) Calculate the heat supplied by the heater.
(b) Calculate the amount of heat flow through piston 1.
(c) If heater were in compartment A, instead of B how would your answers to (a) and (b) change?
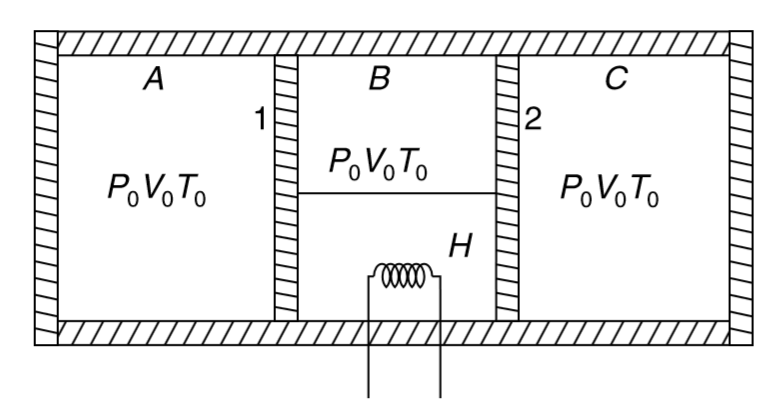 View Solution
View SolutionQuestion 70
An adiabatic cylinder has length 2 L and cross sectional area A. A freely moving non conducting piston of negligible thickness divides the cylinder into two equal parts. The piston is connected to the right face of the cylinder with an ideal spring of force constant k. The right chamber contains 28 g nitrogen in which one third of the molecules are dissociated into atoms. The left chamber container 4 g helium. With piston in equilibrium and spring relaxed the pressure in both chamber is P0. The helium chamber is slowly given heat using an electric heater (H), till the piston moves to right by a distance 3L4. Neglect the volume occupied by the spring and the heating coil. Also neglect heat capacity of the spring.
(a) Find the ratio of CP and CV for nitrogen gas in right chamber.
(b) Calculate change in temperature of helium.
(c) Calculate heat supplied by the heater.
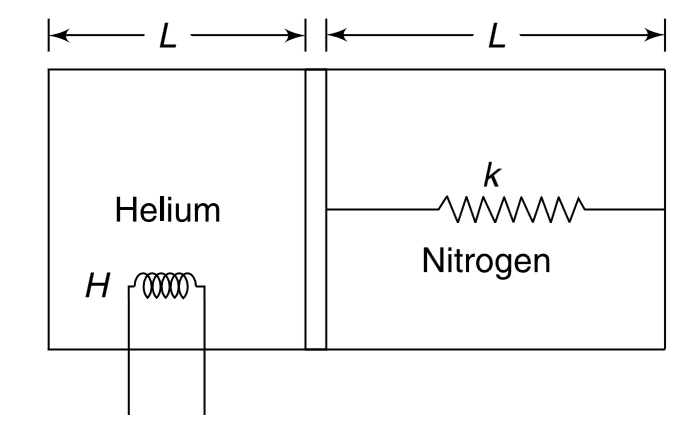 View Solution
View Solution