All Questions from ARIHANT PHYSICS (HINGLISH) FLUIDS for Class 11
| Class 11 | PHYSICS |
| Chapter | FLUIDS |
| ARIHANT PHYSICS (HINGLISH) | All Questions |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
We know that the atmospheric pressure on the surface of the earth is because of weight, of the air. The radius of the earth is 6400 km and atmospheric pressure on the sruface of earth is 1×105N/m2. Estimate the mass of the earth's atmosphere assuming that acceleration due to gravity remains constant at 10m/s2 over the entrie height of the atmospehre. View SolutionQuestion 4

A tightly fitted piston can slide along the inner wall of a long cylindrical pipe. With the piston at the lower end of the pipe, the lower end of the pipe is dipped into a large tank, filled with water. Now the piston is pulled up with the help of the rod attached to it. water rises in the pipe along with the piston. Why? To what maximum height water can be raised in the pipe using this method? What will be the answer to your question if water is replaced with mercuty? Atmosphere pressure is Patm=1.01×105Pa. View SolutionQuestion 5
A hypothetical planet has an ocean of water which is 50km deep. The top 5km is frozen as ice (i.e., 45km is water). Radius and average density of the planet are both half the respective values for the earth. There is no atmospehre. Obtain an estimate of the pressure at the bottom of the ocean. View SolutionQuestion 7
(i) A toy boat made of steel is floating in a beaker having water. The beaker is placed on a spring balance. The boat tilts and sinks into water.
(a) Will the level of water in the beaker go up or fall down?
(b) Will the reding of spring balance decrease or increase?
(iii) You are in a boat on a calm lake. There is a floating log near you . You pick the log and put it into the boat. What happesn to the level of water in the lake? Does it rise or fall? View SolutionQuestion 8
A closed cubical box of negligible mass has large number of spherical balls arranged neatly inside it as shown in the figure. When placed in water, the box floats with 80% of its volume remaining. Submerged. What is specifc gravity of material of the balls? Neglect thickness of the wall of the box.
 View Solution
View SolutionQuestion 9
Two identical containers have the same volume of water in it. Each of them is placed on a balnce and redings of the two balances are same. There is a hollow ball and a solid ball that have same volume. The hollow ball floats in water and the solid ball sinks. A string from the ceiling suspends the solid ball so that it remains completely submerged in the water in the first container. The hollow ball is held submerged in the water in the second container and is held by a stringfastened to the bottom of the container. which balance will show higher reading? How will your answer change if the string in the second container is car?
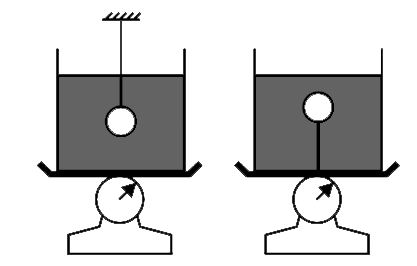 View Solution
View SolutionQuestion 10
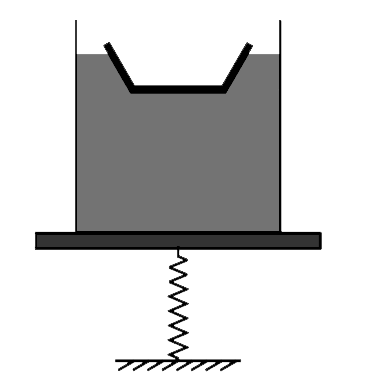
Three tanks T1,T2 and T3 are sitting on three weighing scales s1,s2 and s3 respectively. Tank T1 has a spout, as shown and water has been filled in it to a level just below the spout. The other two tanks are empty. Reading of the three scales are 20kg, 4kg and 3kg respectively A 4kg body is put into the tant T1 and it floats in the water. Now the reading of scale s3 was found to be 4.5kg. what is the reading of other tow scales?
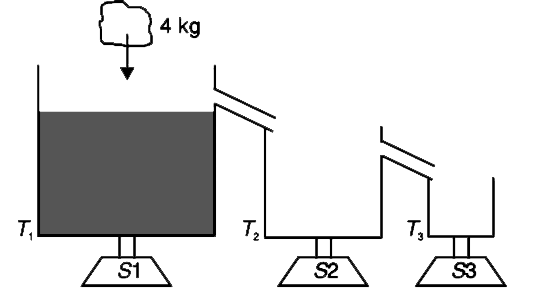 View Solution
View SolutionQuestion 11
A cylindrical block of length 2l is made of two different materials. The uppwer half has density d1 and and lower half, which is heavier, has density d2 the block is floating in a liquid of unknown density d with l2 of its length outside the liquid.
(a) Find d
(b) Show that d>4d13
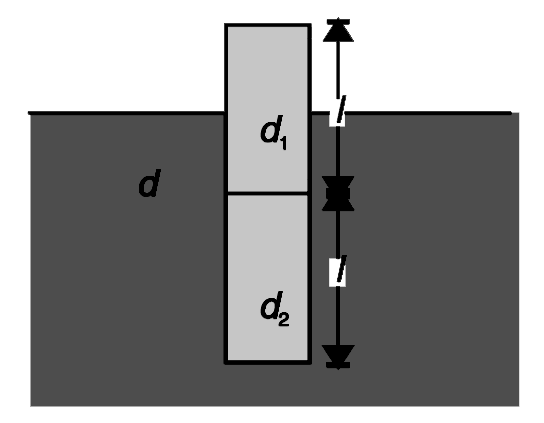 View Solution
View SolutionQuestion 12
A sealed balloon, filled with air, floats in water with 13 of its volume submerged. It was found that if it is pushed inside water at a depth h, it remains in equilibrium, neither sinking nor rising. Find h. Given that height of water barometer is 10m and temperature is constant at all depth.
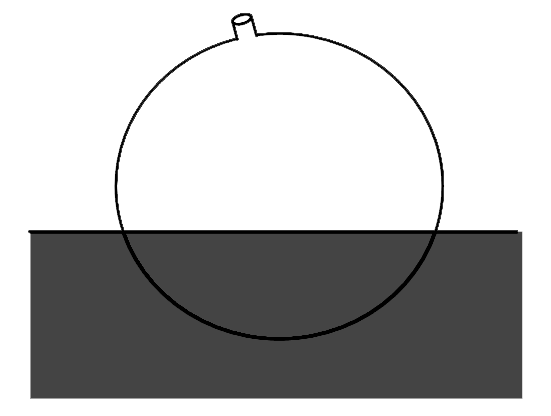 View Solution
View SolutionQuestion 13
Long back our Earth was made of molten material. Assume it to be a uniform sphere of radius R having density d. Take acceleartion due to gravity at the surface to be g and calculate the gauge pressure (P0) at the centre of this fluid Earth. Calculate P0 for following data: R=600 km, d=5500 kg m−3 and g=10ms−2View SolutionQuestion 14
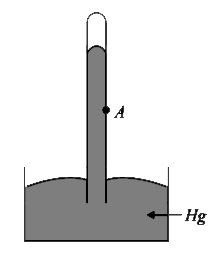
A device used to measure the specific gravity of a liquid is called a hydrogmeter. In a simple hydrometer there is a cylindrical galss tube with some lead-weight at its bottom. The device floats in liquid while remaining vertical. The top part of the tube extends above the liquid and the divisions marked on the tube allows one to directly read the specific gravity of the liquid.

The scale on the tube is calibrated such that in pure water it reads 1.0 at the water surface and a lenght z0 of the tube is submerged. calculate the specific gravity of the liquid if the liquid level is ΔZ above the 1.0 mark. Disregard the curvature of the tube bottom. View SolutionQuestion 16
Two identical communicating containers have water filled into them.A speherical ball of ice (relative density=0.9) having volume 100cm3 is put into the left vessel. Calculate the volume of water flowing into the right container. Immediately after placing the ball (i.e.,don't consider any melting of the ice ball). give your answer for following two caes
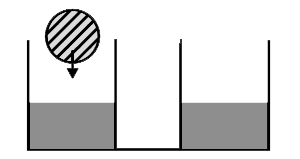
(i) The ice ball floats in the water in the left container.
(ii) The ice ball gets exactly half immersed in the water.
(iii) What will happen to the water level after the ice melts? Answer for bodth i and ii above. View SolutionQuestion 17
An open cyclindrical container has a cross sectiional area A0=150cm2 and water has been filled in it up to a height h. A cylinder made of wood (relative density=0.6) having cross sectional area A=125 cm2 and length 10cm is now placed inside the container with its axis vertical. Find the distance (x) of the base of the wooden cylinder from the base of the container in equilibrium for following three cases:
(a) h=8cm
(b) h=12cm
(c) h=0.8cm
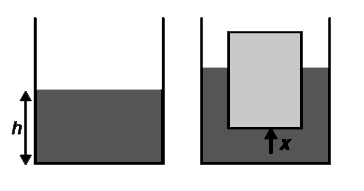 View Solution
View SolutionQuestion 18
A light cylinderical tube of length L=1.5m and radius v=1√πm is open at one end. The tube containing air is inverted and pushed inside water as shown in figure. A block made of material of relative density 2 haas been placed on the flat upper surface of the tube and the whole system is in equilibrium Neglect the weight of air inside the tube and find the volume of block placed on the tube.
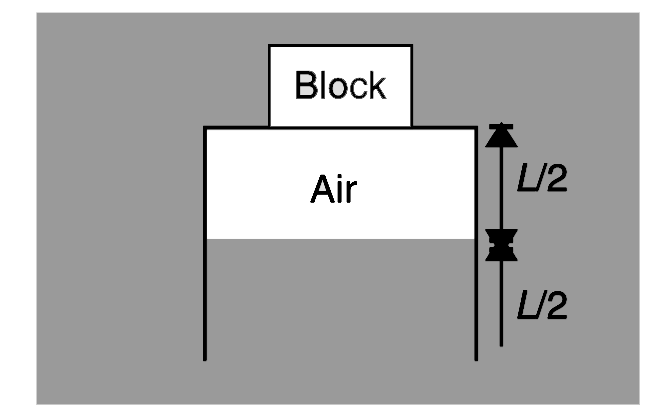 View Solution
View SolutionQuestion 19
A solid wooden cone has been supported by a string inside water as shown in the figure. The radius of the circular base of the cone is R and the volume of the cone is v. In equilibrium the base of the cone is at a depth H below the water surface. Density of wood is d(<ρ, density of water).

(a) Find tension in the string.
(b) Find the force applied by the water on the slant surface of the coone. take atmospheric pressure to be p0.View SolutionQuestion 20
A large container has a sliding vertical wall of height H so as to divide it into two parts. The partition wall is connected to the left container wall by an ideal spring of force constant k. when the spring is relaxed the dimentsions of the floor of the right part is Lxxb. Now water (density ρ) is slowly poured into the right chamber. what is the maximum volume of water that can be stored in the right chamber without spilling it into the other part. The partition wall slides without friction.
 View Solution
View SolutionQuestion 21
A cylindrical container has cross sectional area of 0.20m2 and is open at the top. At the bottom, it has a small hole (A) kept closed by a cork. There is an air balloon tied to the bottom surface of the container. Volume of balloon is 2.2 litre. Now water is filled in the container and the balloon gets fully submerged. Volume of the balloon reduces to 2.0 litre. The cork is taken out to open the hole and at the same moment the whole container is dropped from a large height so as to fall under gravity. Assume that the container remains vertical. find the change in level of water inside the falling container 2 second after it starts falling. View SolutionQuestion 22
A wooden stick of length L, radius R and density ρ has a small metal piece of mass m ( of negligible volume) attached to its one end. Find the minimum value for the mass m (in terms of given parameters) that would make the stick float vertically in equilibrium in a liquid of density σ(>ρ).View SolutionQuestion 23
A rod of length 6m has a mass of 12kg. It is hinged at one end of the rod at a distance of 3m below the water surface.
a.What must be the weight of a block that is attached to the other end of the rod so that 5m of the rod's length is under water?
b. Find the magnitude and direction of the force exerted by the hinge on the rod. The specific gravity of the material of rod is 0.5.
 View Solution
View SolutionQuestion 24
Assume that a car travelling on horizontal straight road with an accelration of a 5 ms−2 has all its windows rolled up and all air vents closed. Length of the car is L=3.0m. By considering a horizontal tube of air that extends from the windshield to th rear surface, and applying Newton's Law on it, calculate the difference in pressure of air at the rear and front of the car. How does this pressure compare with the atmospheric pressure? Density of air ρ=1.2kgm−3View SolutionQuestion 25
A container partially filled with water is moved horizontally with acceleration α=g3. A small wooden block of mass m is tied to the bottom of the container using a string. The block remains inside. Water with the string inclined at an angle θ to the horizontal. Assuming that the density of wood is half the density of water, fnd the angle θ and the tension inthe string.
 View Solution
View SolutionQuestion 26
A cylindrical tank having radius R is half filled with water having density ρ. There is a hole at the top of the tank. The tank is moved horizontally. Perpendiular to its length, with a constant acceleration equal to the acceleration due to gravity (g). Find the maximum pressure exerted by water at any point on the tank. Atmospheric pressure is P0. Assume that there is no spillage. View SolutionQuestion 28
(i) A projected in still air. With respect to the ball the streamlines appear as shwon in the figure. At which point is the pressure larger -1 or 2?

(ii) In the above figure if the ball is also spinning in clockwise sense, in which direction it will get deflected-up or down? View SolutionQuestion 29
(i) In the arrangement shown in the figure, the tank has a large cross section and the pipes have much smaller cross section. The opening at A is unplugged and the water jet hits the ground surface at a horizontal distance x.
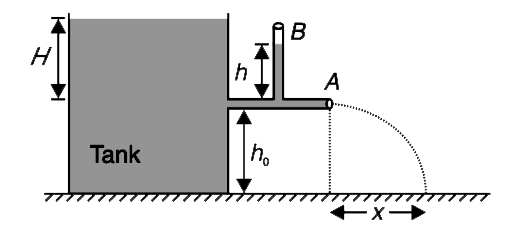
(a) Find the level of water (h) in the tube B as water flows out of A.
(b) Find x.
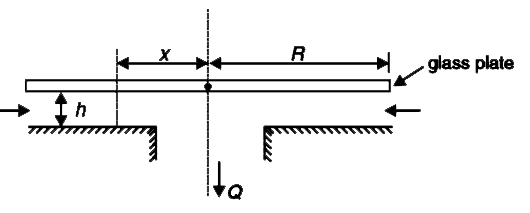
(i) A flat horizontal surface has a small hole at its centre . A circular glass plate of radius R is placed symmetrically above the hole with a small gap h remainng between the plate and the surface A liquid enters the gap symmetrically from all sides and after travelling radially through the gap finally exits from the hole. The volume flow rate of the liquid coming out from the hole is Q (in m3s−1).
(a) If the flow speed just inside the circumference of the circular plate is V0 and the speed (Vx) of flow inside the gap at distance x(see figure) from the centre of the hole.
(b) Write Vx in terms of Q, h and x.
 View Solution
View SolutionQuestion 30
A horizontal tube having cross sectional area A1=10cm2 has a venturi connected to it having cross sectional area A2=4cm2. A moanometer, having mercury as its liquid is connected to be has uniform cross section and it has a horizontal part of lenght L=10cm. When there is no flow in the tube the height of mercuty column in both vertical arms is H=12cm. calculate the minimum flow rate (in m3/s) of air through the tube if it is required that the entire amount of mercury move to one vertical arm of the manometer. Gives, density of Hg=13.6×103kgm3, density of air=1.2 kg m−3.
 View Solution
View SolutionQuestion 31
A liquid is flowing in a horizontal pipe of uniform cross section at a speed v. Two tubes A an B are inserted into the pipe as shown. Assume the flow to remain streamiline inside the pipe.
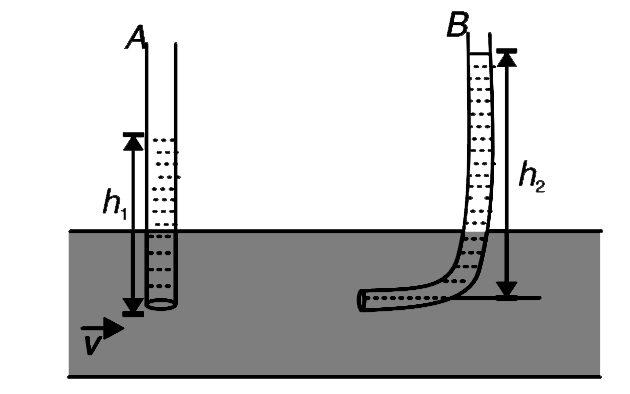
(a) The diagram depicts that height of liquid in tube B(=h2) is more than the height of liquid in tube A(=h1) is it correct?
(b) Calculate the difference in height of the liquid in two tubes. View SolutionQuestion 33
A horizontal glass tube is filled with mercury. The tube thas three different cross sections as shwn: with A1=18cm2,A2=8cm2 and A3=9cm2. The piston is pushed so as to throw out mercury at a constant speed of v=6m/s at the other end of the tube. Assume that mercuty is an ideal fluid with density ρHg=1.36×104kg/m3. Take g=10m/s2Patm=1.01×105Pa

(i) Find the force needed to push the piston assuming that friction force between the piston and the tube wal is f=40N
(ii) Find the height (h) of mercury column in the attached vertical tube. What happens to this height if the piston is pushed with smaller speed? View SolutionQuestion 34
A container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The initial speed of efflux without cylinder is View SolutionQuestion 35
A lake filled with water has depth H, A pipe of length slightly less than H lies at the bottom of the lake. It contains an ideal gas filled up to a length of H10 A smooth an ideal gas filled up to a length gas in place. Now the pipe is slowly raised to vertical position (see figure). Assume that temperature of the gas remains Constant and neglect the atmospheric pressure.
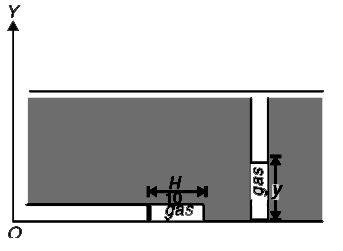
(a) Plot the variation of pressure inside the lake as a function of height y from the base. Let the height of piston frm the base, after the pipe is made vertical, by y. plot the variation of gas pressure as a function of y in the first graph itself.
(b) In equilibrium the gas pressure and the pressure due to water on the piston must be equal. Using this solve for equilibrium height y0 of the piston. You get two answers. Which one is correct and why? View SolutionQuestion 36
A centrifuge has a horizontal cylinder rotating about a vetical axis as shown in the figure. Water inside it has density ρ.
(a) Consider a point A. Inside the liquid, at a distance r from the rotation axis. Liquid pressurea t his point is P. Write the value of dPdr when the cylinder, with all its liquid. rotates uniformly at an angular speed ω.
(ii) Consider a small disc shaped foreign material inside the centrifuge at point A. The area of circular disc is ΔS and its thickness is Δr. It disc is in position so that its circular face is vertical. Find the radial acceleration of the disc with respect to the cylinder when angular speed of rotation is
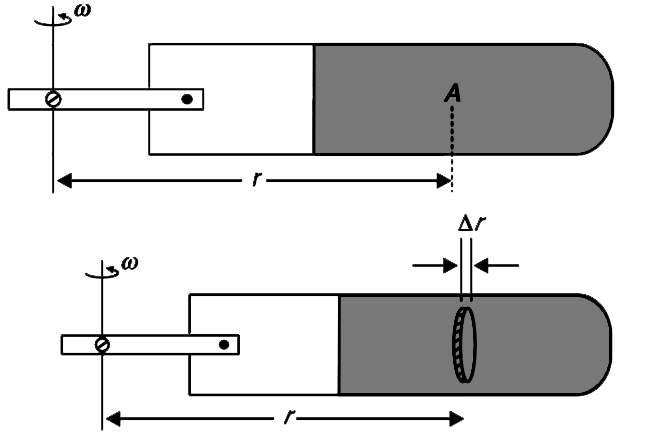 View Solution
View SolutionQuestion 37
(i) A cubical metal block of side 10cm is floating in a vessel contatining mercury. The vesel has a square cross section of side length 15cm. Water is poured into the vessel so that the metal block just gets submerged. Calculate the mass of water that was poured into the vessel. It is given that relative density of the metal and mercury are 7.3 and 13.6 respectively.
(ii) In the last question, in place of water if we poured another liquid of relative density 'r' it was found that when the metal block ws just completely submerged it was no longer touching mercury. what is value of r? View SolutionQuestion 38
A wooden block of cross sectional area A (in shape of a rectangle) has height h. It is held such that its lower surface touches the water surface in a wide and deep tank. The block is released in this positon. It oscillates for some time and then settles into its equilibrium positon. in equilibrium the block floats with its upper face just on the water surface. Calculate the amount of heat generated in the process assuming that the loss in gravitational potential energy of the system coprising of water and the block gets converted into heat. Density of water is ρ.
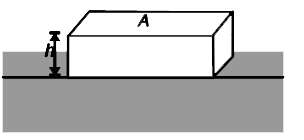 View Solution
View SolutionQuestion 41
A spherical pot with a small opening at top has a mass of M=452.1 gram. It floats in water while remaining exactly half submerged A small coin of amss m=5gram is dropped into the pot. Find how much more the pot will sink. Express your answer in terms of change in height of the pot that is under water. =1g/cc.
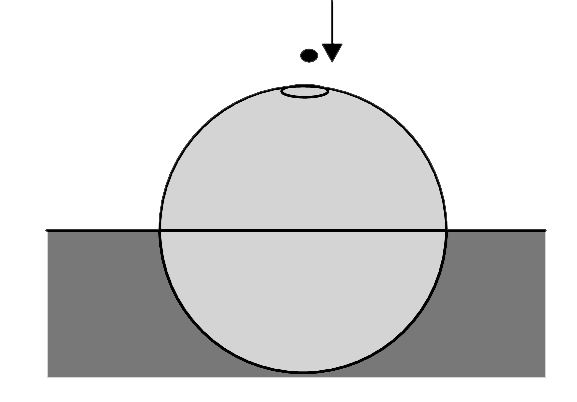 View Solution
View SolutionQuestion 42
A cylindrical wooden block of density half the density of water is floating in water in a cylindrical container. The cross section of the wooden block. And its height are A and h respectively. The cross sectional area of the container is 2A. The wooden block is pushed vertically so that it gradually gets immersed in water. Calculate the amount of work done in pushing the block. Density of water =ρ0.
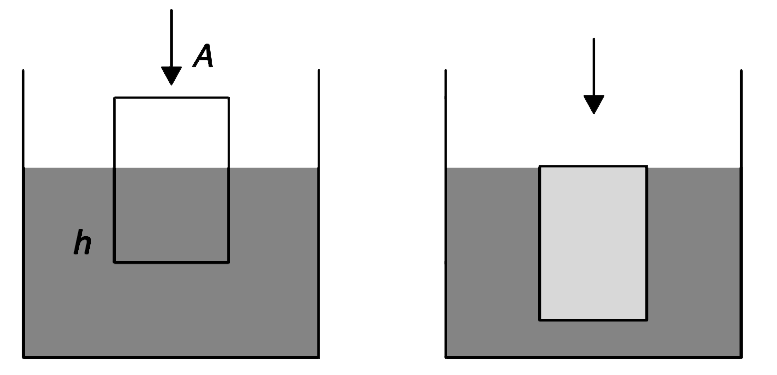 View Solution
View SolutionQuestion 43
A cylindrical container has mass M and height H. the centre of mass of the empty container is at height H2 from the base. A liquid, when completley filled in the container, has mass M2 this liquid is poured in the empty contaienr.
(a) How does the centre of mass of the system (container+liquid) move as the height (x) of liquid column changes from zero to H? Explain your answer qualitatively. Draw a graph showing the variation of height of centre of mass of the system (xcm) with x.
(b) Find the height of liquid column x for which the centre of mass is at its lowest position.
 View Solution
View SolutionQuestion 45
A cyclindrical ice block is floating in water 10% of its total volume is outside water. Kerosene oil (relative density=0.8) is poured slowly on top of water in the container. Assume that the oil does not mix with water. Height of the ice cylinder is H.
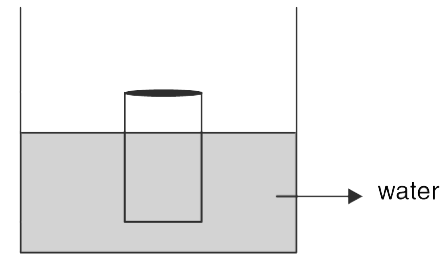
(a) As kerosene is poured, how does the volume of ice block above the water level change?
(b) What is the thickness of kerosene layer above the water when 20% of the volume of the ice block is above the water surface?
(c) Find the ratio of voume of ice block is kerosene to its volume in water after the kerosene layer rises above the top surface of ice and the block gets completely submerged. Neglect any melting of ice. View SolutionQuestion 46
A cylindrical container contains water. A cubical block is floating in water with its lower surface connected to a spring.
(a) Suppose that the spring is in relaxed state. Now, if the whole contaienr is accelerated vertically upwards. Will the spring get compressed?
(b) Suppose that the spring is initially compressed. Now, what will happen to the state of the spring when the container is accelerated upwards?
(c) Assume that mass of the block is 1 kg and initially the spring (force constant k=100 N/m) is compressed by 5cm. when the container is accelerated up by an acceleration of 5m/s2, the spring has a total compression of 6cm. Calculate the chnag ein volume of block submerged inside water when the container gets accelerated. Density of water is 103kg/m3.
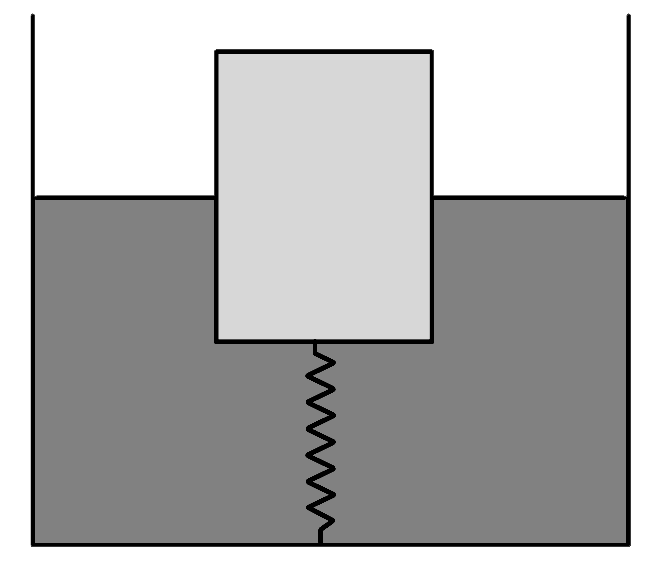 View Solution
View SolutionQuestion 47
A water tank has a circular hole at its base. A solid cone is used to plug the hole. Exactly half the height of the cone protrudes out of the hole. Water is filled in the tank to a height equal to height of the cone. Caluclate the buoyancy force on the conc. Density of water is ρ and volume of cone is V.
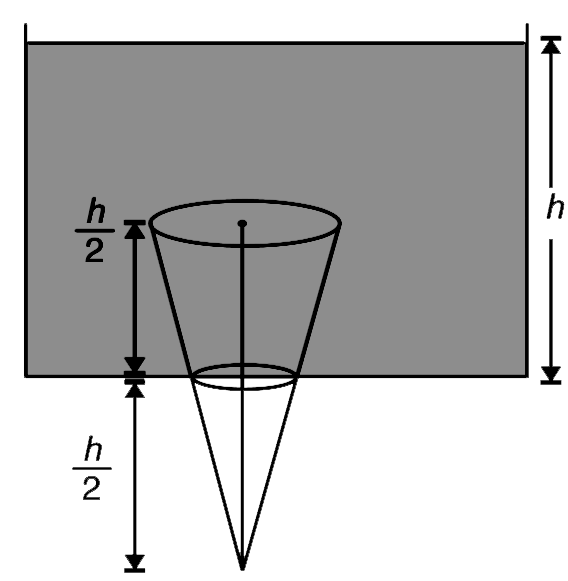 View Solution
View SolutionQuestion 48
A cylindrical tank has a mass of the 200kg and inner radus of r=2.0m. The tank has no bottom and is directly bolted to the floor (B1 and B2 are bolts in the figure.) the tank is connected to an elevated open tank and both the tanks are filled withh a liquid as shown in the figure. various heights are as shown. When a small wooden cube of specific gravity 0.6 is placed in the upper tank, it floats while remaining exactly half submerged Calculate the force applie dby the bolts in holding the tank.
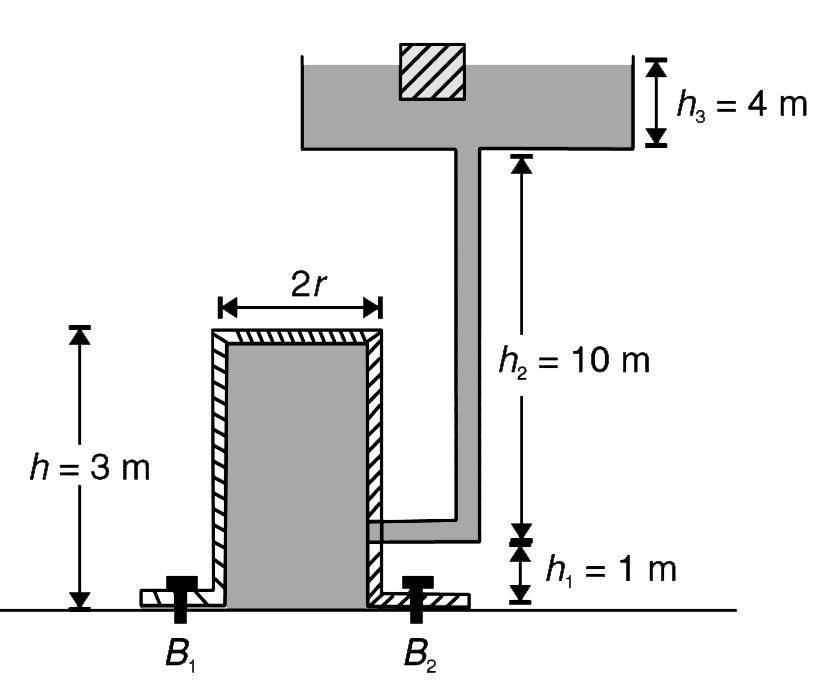 View Solution
View SolutionQuestion 49
(i) A non uniform cube of side length a is kept inside a container as shown in the figure. The average density of the material of the cube is 2 ρ where ρ is the density of water. Water is gradually fille din the container. It is observed that the cube begins to topple, about its edge into the plane of the figure passing through pointA, when the height of the water in the container becomes a2. Find the distance of the centre of mass of the cube from the face AB of the cube. Assume that water seeps under the cube.
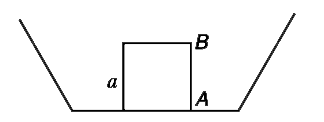
(ii) A rectangular concrete block (specific gravity =2.5) is used as a retatining wall in a reservoir of water. The height and width of the block are x and y respectively the height of water in the reservoir is z=34x. the concrete block cannot slide on the horizontal base but can rotate about an axis perpendicular to the plane of the figure and passing through point A
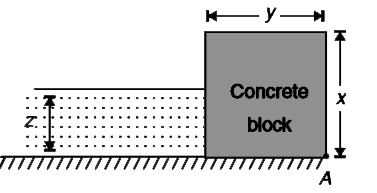
(a) Calculate the minimum value of the ratio yx for which the block will not begin to overturn about A.
(b) Redo the above problem for the case when there is a seepage and a thin film of water is present under the block. Assume that a seal at A prevents the water from flowing out underneath the block. View SolutionQuestion 50
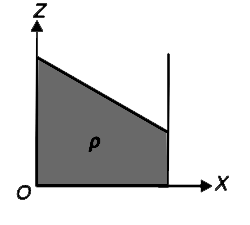
A contaienr havng an ideal liquid of density ρ is moving with a constant acceleration of ˆa=axˆi+azˆk where x direction is horizontal and z is vertically upwards. The container is open at the top. In a reference frame attached to the contaienr with origin at bottom corner (see figure), write the pressure at a point inside the liquid at co-ordinates (x,y,z). The pressure is P0 at origin.
 View Solution
View SolutionQuestion 51
A cubical contaienr of side length L is filled completely with water. The container is closed. It is acclerated horizontally with acceleration a. Density of water is ρ.
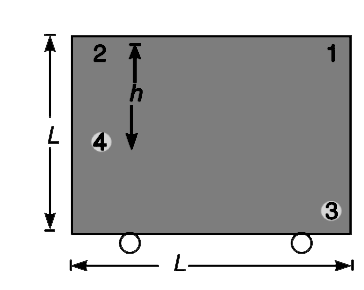
(a) Assuming pressure at point 1 (upper right corner) to be zero, find pressure at point 2 (upper left corner).
(b) Pressure at point 4, at a distance h vertically below point 2 , is same as pressure at lower right corner 3. find h. View SolutionQuestion 52
An open rectangular tank 5mxx4mxx3m in dimension is containing water up to a height of 2m the tank is accelerated horizontally along the longer side. Assuming water to be and ideal liquid find-
(a) the maximum acceleration with which the tank can be moved so that water does not fall from the rear side.
(b) the gauge pressure at the bottom of the front and back of the tank (points A and B) if the tank is closed at the top and is then acclerated horizontally at 9m/s2. Assume that the top cover has a small hole at the right side of the tank so taht pressure of air inside the tank is maintained at atmospheric pressure. Gauge pressure at a point is difference in absolute pressure at the point and atmospheric pressure.
 View Solution
View SolutionQuestion 53
A water clock consist of a vessel which has a small orifice O. The upper contaienr is filled with water which trickless down into the lower contaienr. The shape of the (upper or lower) contaienr is such that height of water in the upeer container changes at a uniform rate. What should be the shape of the container? Assume that atmospheric air can enter inside the lower container through a hole in it taht the upper container is open at the top. Vessel is axially symmetric.
 View Solution
View SolutionQuestion 56
A cylinder of length L floats with its entire length immersed in two liquids as shown in the fig.
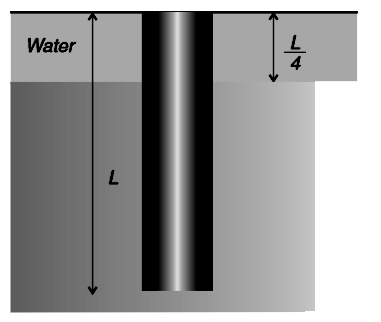
The upper liquid is water and the lower liquid has density twice that of water. The two liquid are immiscible. The cylinder is in equilibrium with its 34 lenght in the denser liquid and 14 of its length in water. The thickness of water layer is L4 only. Find.
(a) the specific gravity of the material of the cylinder.
(b) the time period of oscillations if the cylinder is depressed by some small distance (<L4) and released. Neglect viscosity and change in level of liquids when the cylinder moves. View SolutionQuestion 57
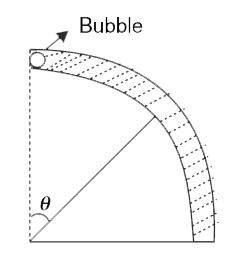
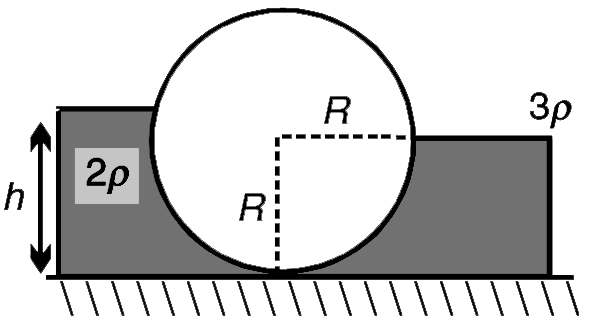
(i) In the figure shown, the heavy cylinder (radius R) resting on a smooth surface separates two liquids of densities 2ρ and 3ρ. Find the height 'h' for the equilibrium of cylinder.
(ii) The cross section of a dam wall is an arc of a circle of radius R=20m subtending on angle of θ=60∘ at the centre of the circle. the centre (O) of the circle lies in the water surface. The width of the dam (i.e., dimension perpendicular to the figure) is b=10m. Neglect atmospheric pressure is following calculations.
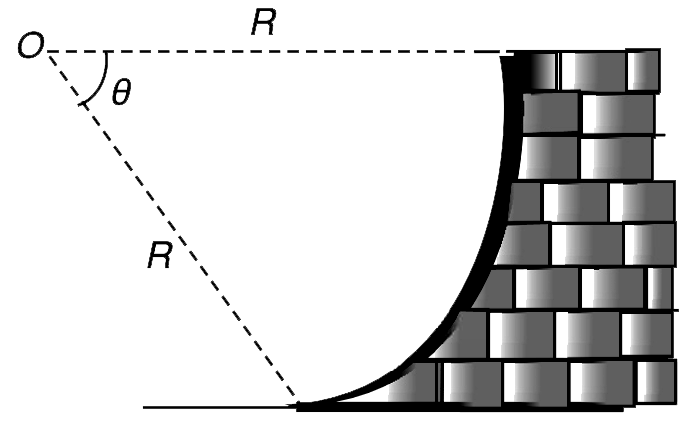
(a) Calculate the vertical component of force (Fx) applied by water on the curved dam wall.
(b) Calculate the horizontal component of force (FH) applied by water on the curved dam wall.
(c) Calculate the resultant force applied by the water on the curved dam wall. View SolutionQuestion 58
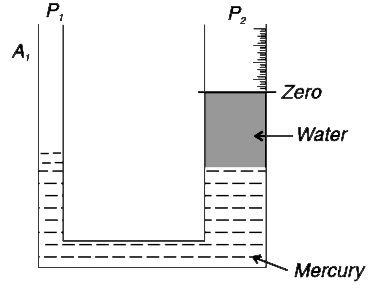
A monometer has mercuty and water filled in it as shown in the figure A scale is marked on the right tube which has a cross sectional area of A2. The other tube has a cross sectional area of A1. When pressures P1 and P2 at both ends of the manometer is same, the level of water in the right side is at the zero of the scale. When the applied pressure P1 is changed by ΔP0, the level of water surface changes by Δh. the quantity ΔhΔP0 can be defined as pressure sensitivity(s) of the manometer. Calculate the pressure sensitivity of the given manometer. Density of water and mercury is ρω and ρHg respectively.
 View Solution
View SolutionQuestion 59
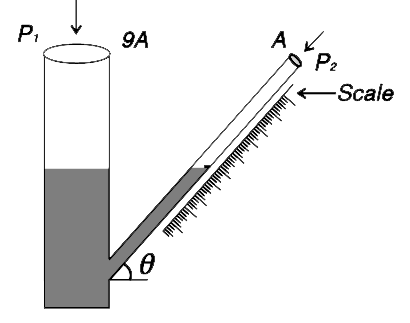
A manometer has a vertical arm of cross sectional area 9A and an inclined arm having area of cross section A. The density of the manometer liquid has a specific gravity of 0.74. the scale attached to the inclined arm can read up to ±0.5mm. It is desired that the manometer shall record pressure difference (P1−P2) up to an accuracy of ±0.09 mm of water. To acheive this, what should be the inclination angle θ of the inclined arm.
 View Solution
View SolutionQuestion 60
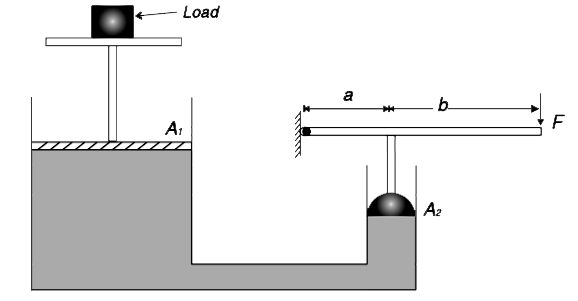
The figure shows a schematic layout of hydraulic jack. The load to be raised weighs 20,000N. The area of cross section of the two pistons are A1=50cm2 and A2=10cm2. The force (F) is applied at theend of a ligh lever bar as shown in the figure. Lenghts a and b are 4cm and 36cm respectively. Find the force (F) required to raise the load slowly.
 View Solution
View SolutionQuestion 62
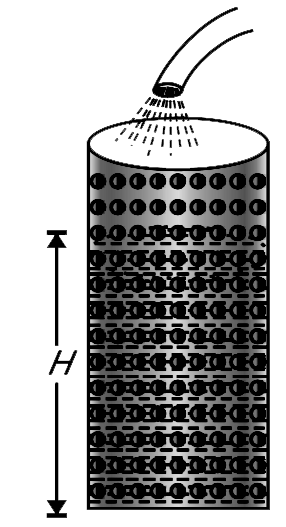
A cylinderical container having radius r has perforated wall. There are large number of uniformly spread small holes on the vertical wall occupying a fraction η=0.02 of the entire area of the wall. To maintain the water level at height H in the contaienr water is being fed to it at a cosntant rate Q(m3s−1). find q.
 View Solution
View SolutionQuestion 63
A syringe is filled with water. Its volume is V0=40cm2 and cross section of its interior is A=8cm2. The syrings is held vertically such that its nozzle is at the top, and its piston is pushed up with constant speed. Mass of the piston is M=50 g and the water is ejected at a speed of u0=2m/s. cross section of the stream of water at the nozzle is a=2mm2. Neglect friction and take the density of water to be ρ=103kg/m3
(a) Find the speed of the piston
(b) Find the total work done by the external agent in emptying the syringe. View SolutionQuestion 64
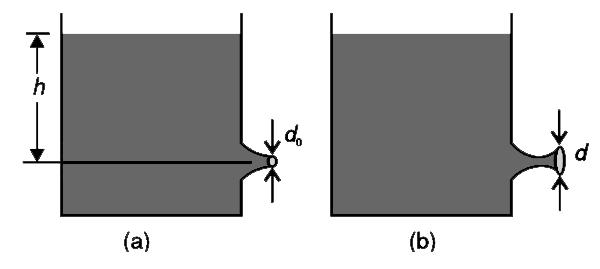
A water tank has a small hole in its wall and a tapering nozzle has been fitted into the hole (figure). The diameter of the nozzle at the exit is d0=1cm. The height of water in the tank above the central line of the nozzle is h=2.0m.
Calculate the dischargerate in m3s−1 through the nozzle. Another nozzle which is diverging outwards is fitted smoothly to the first nozzle. The pressure at the neck of the two nozzle (where diameter is d0) drops ot 2.5m of water. Calculate the exit diameter (d) of the nozzle.
Atmosphere pressure =10m of water and g=10ms−2
 View Solution
View SolutionQuestion 65
There are two large identical open tanks as shown in figure. In tanks 1 there is a small hole of cross sectional area A at its base. Tank II has a similar hole, to which a pipe of length h has been connected as shown. The internal cross sectional area of the pipe can be considered to be equal
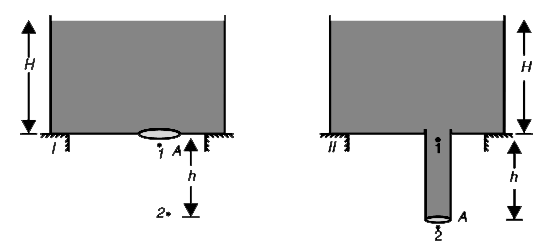
to A. Point 1 marked in both figures, is a point just below the opening in the tank and point 2 marked in both figures, is a point h below point 1 (In fig II, point 2 is just outside the opening in the pipe)
(a) Find the speed of flow at point 2 in both figures.
(b) Find the ratio of speed of flow at point 1 is first the ratio of speed of flow at point 1 is first figure to that in second figure.
(c) Find the difference in pressure at point 1 in both figures. View SolutionQuestion 66
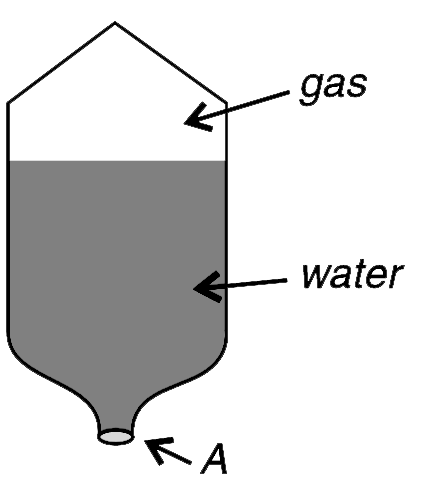
To illustrate th principle of a rocket, a student designed a water rocket as shwon in the figure. It is basically a container having pressurized gas in its upper part and water in its lower part. Pressure of the gas is 4.0Mpa. Mass of empty container is 1.0kg and mass of its content is also 1.0kg. The nozzle at the bottom is opened to impart a vertical acceleration to the contaienr. If it is desired that the initial upwards acceleration of the container be 0.5g. what should be the cross sectional area (A) of the exit of the nozzle?
Neglect the pressure due to height of water in the contaienr and take atmospheric pressure to be 1.0MPa. g=10ms−2.
 View Solution
View SolutionQuestion 67
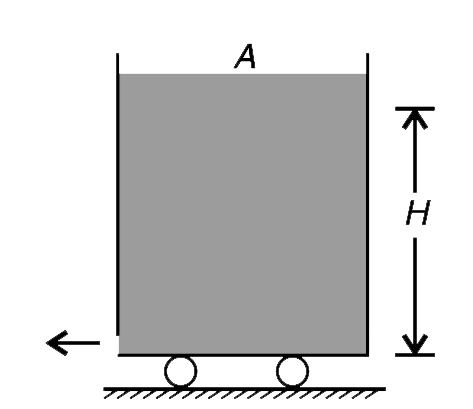
An open tank of cross sectional area A contains water up to height H. It is kept on a smooth horizontal surface. A small orifice of area A0 is punched at the bottom of the wall of the tank. Water begins to drainout. Mass of the empty tank may be neglected.
(i) Prove that the tank will move with a constant acceleration till it is emptied. Find this acceleration.
(iii) Find the find speed acquired by the tank when it is completely empty.
 View Solution
View SolutionQuestion 68
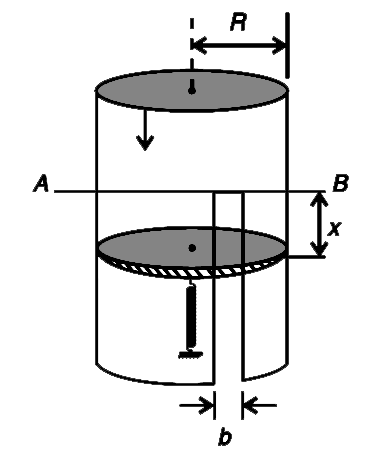
The device shown in fiugre can be used to measure the pressure and volume flow rate when a person exhales. There is a slit of width b running down th length of the cylinder. Inside the tube there is a light movable piston attached to an ideal spring of force constant K. In equiilibrium position the piston is at a position where the slit starts (shown by line AB in the figure. A person is made to exhale into the cylinder causing the piston to compress the spring. Assume that slit width b is very small and the outflow area is much smaller tan the cros section of the tube, even at the pistons full extension. A person exhales and the spring compresses by x. (Density of air=ρ)
(a) Calculate the gage pressure in the tube.
(b) Calculate the volume flow rate (Q) of the air.
 View Solution
View SolutionQuestion 69
(i) Air (density=ρ) flows through a horizontal venturi tube that discharges to the atmosphere. The area of cross section of the tube is A1 and at the constriction it is A2. The constriction is connected to a water (density=ρ0) tank through a vertical pipe of lenght H. Find the volume flow rate (Q) of the air through tube that is needed to just draw the water into the tube.
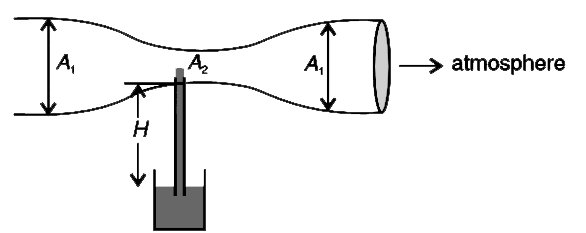
(ii) A non viscous liquid of constant density ρ flows in a stremline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in the figure. The area of cross section of the tube at two points P and Q at heights of h1 and h2 are respectively A1 and A2. The velocity of the liquid at point P is v. Find the work done on a small volume ΔV of fluid by the neighbouring fluid as the small volume moves from P to Q.
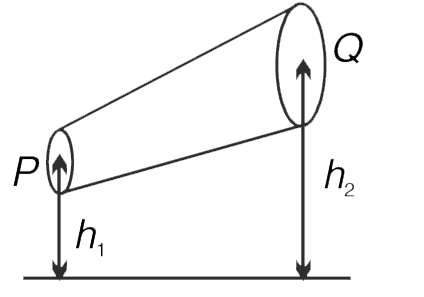 View Solution
View SolutionQuestion 70
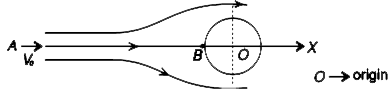
The figure shows a non-viscous, incompressible and steady flow in front of a sphere. A-B is a horizontal streamline. It is known that the fluid velocity along this streamline is given by V=V0(1+R3x3).V0 is velocity of flow on this streamline when x→(−∞). It is given that pressure at x→(−∞) is P0 and density of liquid is ρ.
(i) Write the variation of pressure along the streamline from pointA, far away from the sphere, to point B on the spehre.
(ii) Plot the variation of pressure along the streamline from x=−∞ to x=-R.
 View Solution
View SolutionQuestion 71
There are two tanks next to each other having cross sectional area A1 and A2. They are interconnected by a narrow pipe having area of cross section equal to A0. Initial height of water in the two tanks is h1 and h2 meaured from the level of the pipe. Assume that the flowis ideal and behaves in a way similar to the discharge in air. Calculate the time needed for the water level in two tanks to become same.
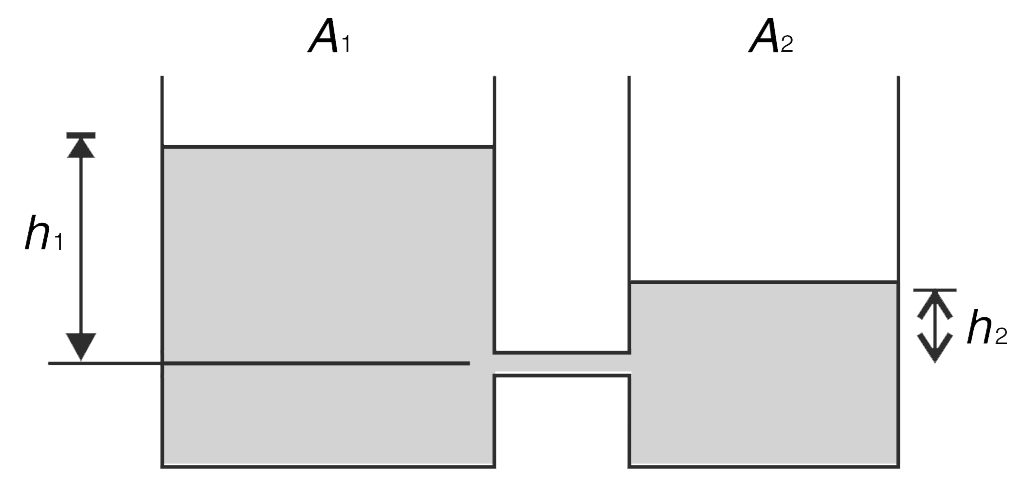 View Solution
View SolutionQuestion 72
A siphon is used to drain water (density=ρ) from a wide tank. The inlet and outlet mouth of the siphon are at the same horizontal level and the highest point of the siphon tube is at a height H from the mouth of the tube. Height of water in the tank above the tube mouth is h (see fig). Atmospheric pressure is P0.
(a) Will the water drain out in this siphon? if yes, at what speed (V)?
(b) Find pressure at the top of the siphon tube (call in P)
(c) Find pressure just inside the left mouth of the tube.
(d) If left part of the tube is slightly cut short, without disturbing anything else, what effect it will have on V and P?
(e) If the right end of the tube is lowered by adding more lenght of tube, it was observed that flow stops when lenght of right limb of the tube becomes H0. Find H0.
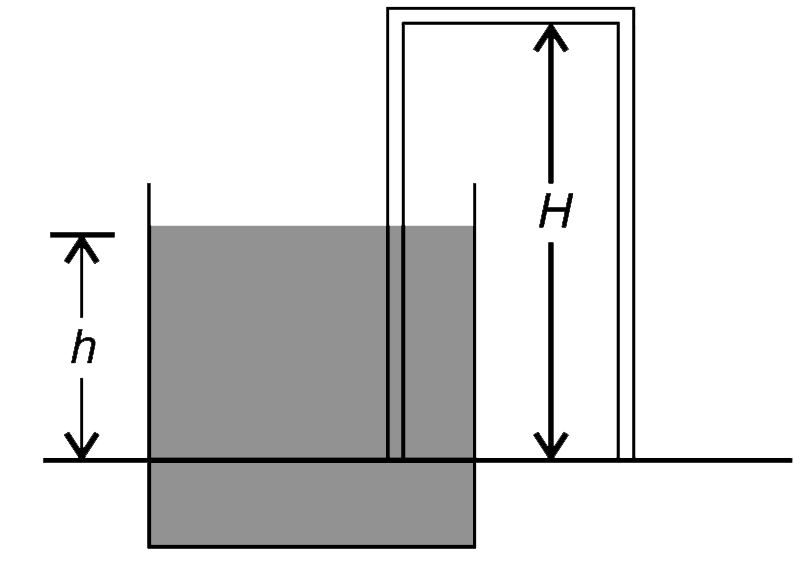 View Solution
View SolutionQuestion 73
A vessel of volume V0 is completely filled with a salt solution having specific gravity σ0. Pure water is slowly added drop by drop to the container and the solution is allowed to overflow.
(a) Find the specific gravity of the diluted solution in the contaienr when a volume V of pure water has been added to it.
(b) If σ0=1.2 then find the specific gravity of the solution in the container after a volume V0 of pure water has been added to it.
(c) Plot the variation of σ with V. View SolutionQuestion 74
A hemispherical bowl of radius R is placed upside down on a flat horizontal surface. There is a small hole at the top of the inverted bowl. Through the hole, a liquid of density ρ is poured in. Exactly when the container gets full, water starts leaking from between the table and the edge of the container. Find the mass (m) of the contaienr.
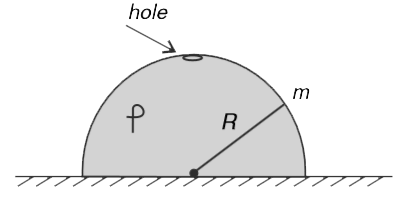 View Solution
View SolutionQuestion 75
A plate is in the shape of a quarter cylinder of radius R and length L. This plate is hinged at C to a vertical wall and can rotate freely about C. The end A of the plate is tied to the wall using two horizontal cables the other cables is parallel to OA and the two cables are placed symmetrically). the space between the wall and the plate is filled completely with water (density=ρ) Neglect the weight of the plate and calculate the tension in each cable .
TAke tan−1(π2)=57∘ and cos57∘=12
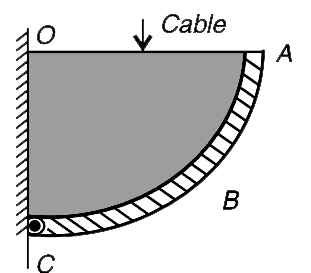 View Solution
View SolutionQuestion 76
A spherical ball of the radius R is made by joining two hemispherical parts. The two parts have density ρ and 2ρ. When placed in a water tank, the ball floats while remaining completely submered.
(a) If density of water is ρ0, find ρ
(b) Find the time period of small angular oscillations of the ball about its equilibrium position. Neglect viscous forces.
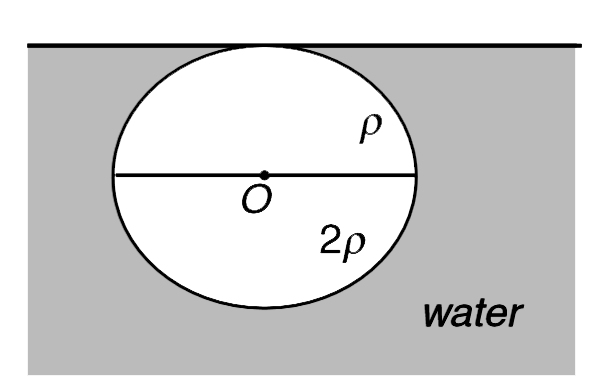 View Solution
View SolutionQuestion 77
In a machine, a fluid from a compressor, which is at high pressure, is allowed to pass through a nozzle. Cross section of the nozzle is shown in the fiuge. The nozzle consists of two sections of radii r1 and r2. The nozzle is fixed on a stand with the help of a clamp. the clamp is a circular ring of radius r1 and width b. The fluid from the compressor is at a presssure of n times the atmospheric pressure p0. assume that the entrie system is horizontal the fluid is ideal and the flow is steady.
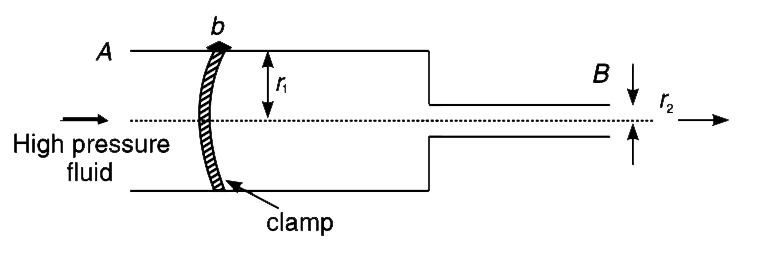
(a) what should be the volume flow rate so that pressure of the fluid at end B reduces to half of its value at end A?
(b) If the entire system is kept in gravity free space and the net force on the nozzle due to the fluid flow is F then determine the minimum radial pressure that should be applied on the clamp. so the nozzle remains in place. Coefficient of friction betwwen clamp and nozzle is μ.
(c) If a small hole is punched anywhere on the thinner part of the nozzle (close to end B) what should be the volume flow rate of the fluid so that it does not gush out? View Solution