Eexercies from BHARATI BHAWAN PHYSICS (HINGLISH) SIMPLE HARMONIC MOTION for Class 11
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| BHARATI BHAWAN PHYSICS (HINGLISH) | Eexercies |
| Medium | English |
| Academic Year | 2023-2024 |
Question 12
The balance wheel of a watch vibrates with an angualr amplitude π radians and a period of 0.5s. Find a) the maximum angular speed of the wheel, b) the angular speed of the wheel when its displacement is π2 radians and c) the angular acceleration of the wheel when its displacement is π4 radians.
[hint: use formulae of linear SHM for the angular SHM of the wheel]View SolutionQuestion 13
A block is on a piston, which executes simple harmonic motion in the vertical plane with a period of 1s. At what amplitude will the block and the piston separate? If the piston has an amplitude of 0.05m, what is the maximum frequency at which the black and piston will remain in contact continously?
[hint: the block and piston will separate when acceleration of piston = acceleration due to gravity.]View SolutionQuestion 15
Two springs of force constants k1 and k2 are joined together and the combination is attached to a mass m resting on a frictionless table at one end and clamped to a fixed support at the other. Show the frequency of oscillation of the mass is f=12π√k1k2(k1+k−(2))m
[Hint: Let the mass be displaced by x and the clamped end of the second spring by x′. Then mf = −k1(x−x′). Considering the first spring and the mass as a single system we have mf =−k2x′]View SolutionQuestion 16
Two springs of force constants k1 and k2 are attached to two opposite sides of a cube of mass m resting on a frictionless table and clamped to two supports at their other ends. Show that if the cube is displaced a little it will execute simple harmonic motion of frequency f=12π√k1+k2m View SolutionQuestion 17
A point of mass m is suspended at the end of a massless wire of length l and cross-section A. If Y is the Young's modulus for the wire, obtain the frequency of oscillation for the simple harmonic motion along the vertical line.
[Hint: If x is the displacement of mass m from the equilibrium position then Y=stressstra∈=FAxl or F = (YAx)/(l) and this force acts opposite to x. Now proceed as in example 3. View SolutionQuestion 19
An ideal gas enclosed in a vertical cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross - section area A. When the piston is in equilibrium, the volume of the gas is (V0) and the its pressure is (P0). The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, Show that the piston executes simple harmonic motion and find the frequency of oscillations. View SolutionQuestion 20
If the mass of a spring, m, is not negligible but small compared to the mass M suspended from it, show that the period of oscillations is given by T=2π√(M+m3)/k, where k is the force constant of the spring.
[Hint: If x and v be the instaneous displacement and velocity of the lower end, then the displacement of an element at a distance z from the fixed end is xz/l and velocity zv/l. The kinetic energy of the spring = (∫t0)12(mdzl)z2v2l2=16mv2
Total energy of the system = 16mv2+12Mv6(2)+12kx2 = a constant. Differentiate anmd find T.]View SolutionQuestion 21
A solid cylinder of mass m is attached to a horizontal spring with force constant k. The cylinder can roll without slipping along the horizontal plane. (See the accompanying figure.) Show that the center of mass of the cylinder executes simple harmonic motion with a period T=2π√3m2k, if displaced from mean position.
 View Solution
View SolutionQuestion 23
A plank rests symmetrically on two cylinders which are separated by a distance of 2l and rotate with uniform speed in opposite direction. If the plank is displaced a little and then released, show that the motion of the plank is simple harmonic. Calculate the period of oscillations of the peak. The co-efficient of friction between the plank and either cylinder is μ.View SolutionQuestion 25
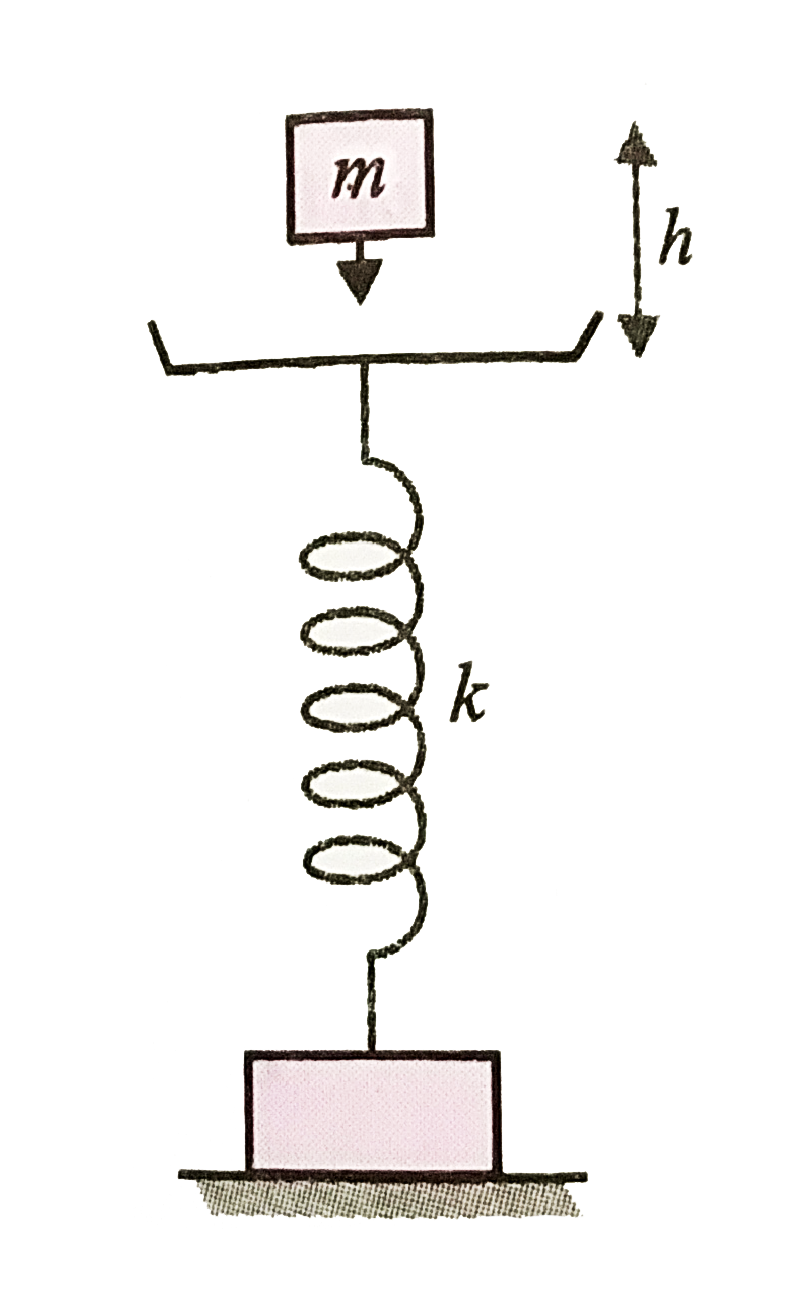
A body of mass m falls from a height h on to the pan of a spring balance, figure, The masses of the pan and spring are negligible. The spring constant of the spring is k. The body gets attached to the pan and starts executing S.H.M. in the vertical direction. Find the amplitude and energy of oscillation.
 View Solution
View SolutionQuestion 28
A small block of mass m resting at the bottom of a hemispherical cup of radius R is displaced a little and released. Determine the period of oscillations of the block, assuming the cup to be smooth and fixed rigidly to the table on which it rests. How will period change if the cup is free to move on the table, it is smooth and its mass is M? View SolutionQuestion 32
A plank with a body of mass m places on it starts moving straight up according to the law y=a(1−cosωtt), whee y is the displacement from the initial position, ω=11s−1. Find :
(a) the time dependence of the force that the body exerts on the plank if a=4.0cm, plot this dependence,
(b) the minimum amplitude of oscillation of the plank at which the body starts falling behind the plank,
(c) the amplitude of oscillation of the plank at which the body springs up to a height h=50cm relative to the initial position (at the moment t=0). View SolutionQuestion 33
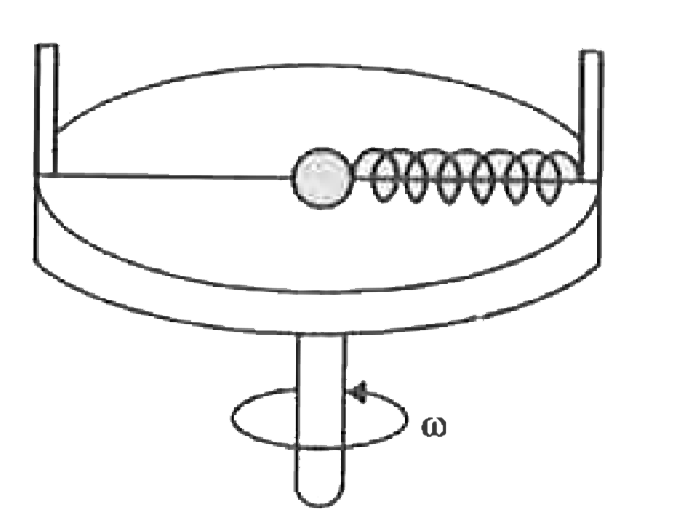
A small sleeve of mass m=1/10kg can move along the diameter of a horizontal disc, which slides without friction along a guide rode. The sleeve is tied to the end of the rod with the aid of a massless spring whose force constant k=10N/m. When the spring is not under tension, the sleeve is at the oscillations of the sleeve when the disc rotates about its axis at the angular speed ω equal to a) 6 rad/s, b) 15 rad/s.
 View Solution
View SolutionQuestion 34
A string of length l=1m and tensioned by a weight M = 4kg has two masses, each of mass = 10g, attached to it at distance l4 and 34 from one of the ends. Find the frequency of oscillations of the masses in the two cases.
a) When the masses are displaced equally in the same direction b) when the masses are displaced equally in opposite directions. View SolutionQuestion 35
A block of mass m1=1kg is attached to a spring of force constant k=24N/cm at one end and attached to a string tensioned by mass m2=5kg . Dedcue the frequency of oscillaitons of the system. If m2 is initially supported in hand and then suddenly released, find

(a) instantaneous tension just after m2 is released . ltbr> (b) the maximum displacement of m1.
(c) the maximum and minimum tensions in the string during oscillations. View SolutionQuestion 36
A rubber cord of force constant k = 100 N/m and l=1m is attached to a particle of mass m = 1kg at one end and fixed to a vertical wall at the other. The body is displaced by x0 = 25cm so as to stretch the cord and then released. Calculate the time particle takes to reach the wall. View SolutionQuestion 38
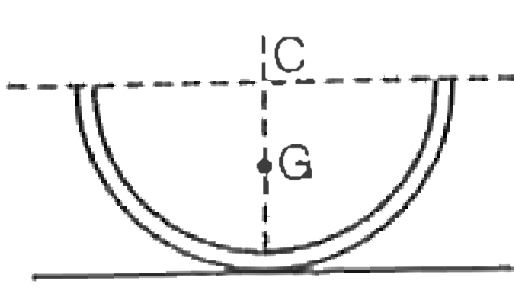
A pipe in the form of a half ring is placed on a horizontal surface. If it is rotated through a small angle, and then released, assuming that it rolls without sliding determine the period of oscillations. The center of gravity of such a body is at distance 2rπ) from the center where r is the radius of the ring.
Hint: (→–––(c)=αrˆi and
→ac=→ac+(→aG/c)tangent+(→aG/c)normal
 View Solution
View SolutionQuestion 39
An endless cord consists of lengths 2l and 2l′ and their masses per unit length are m and m′. It is placed in stable equilibrium over a smooth peg as shown in the figure. It is slightly displaced and left to itself. Show that motion is simple harmonic. Find the period of oscilattions.
 View Solution
View Solution