Linked Comprehension from CENGAGE PHYSICS (ENGLISH) Chapter 20 RIGID BODY DYNAMICS 2 for Class 11
| Class 11 | PHYSICS |
| Chapter | RIGID BODY DYNAMICS 2 |
| CENGAGE PHYSICS (ENGLISH) | Linked Comprehension |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
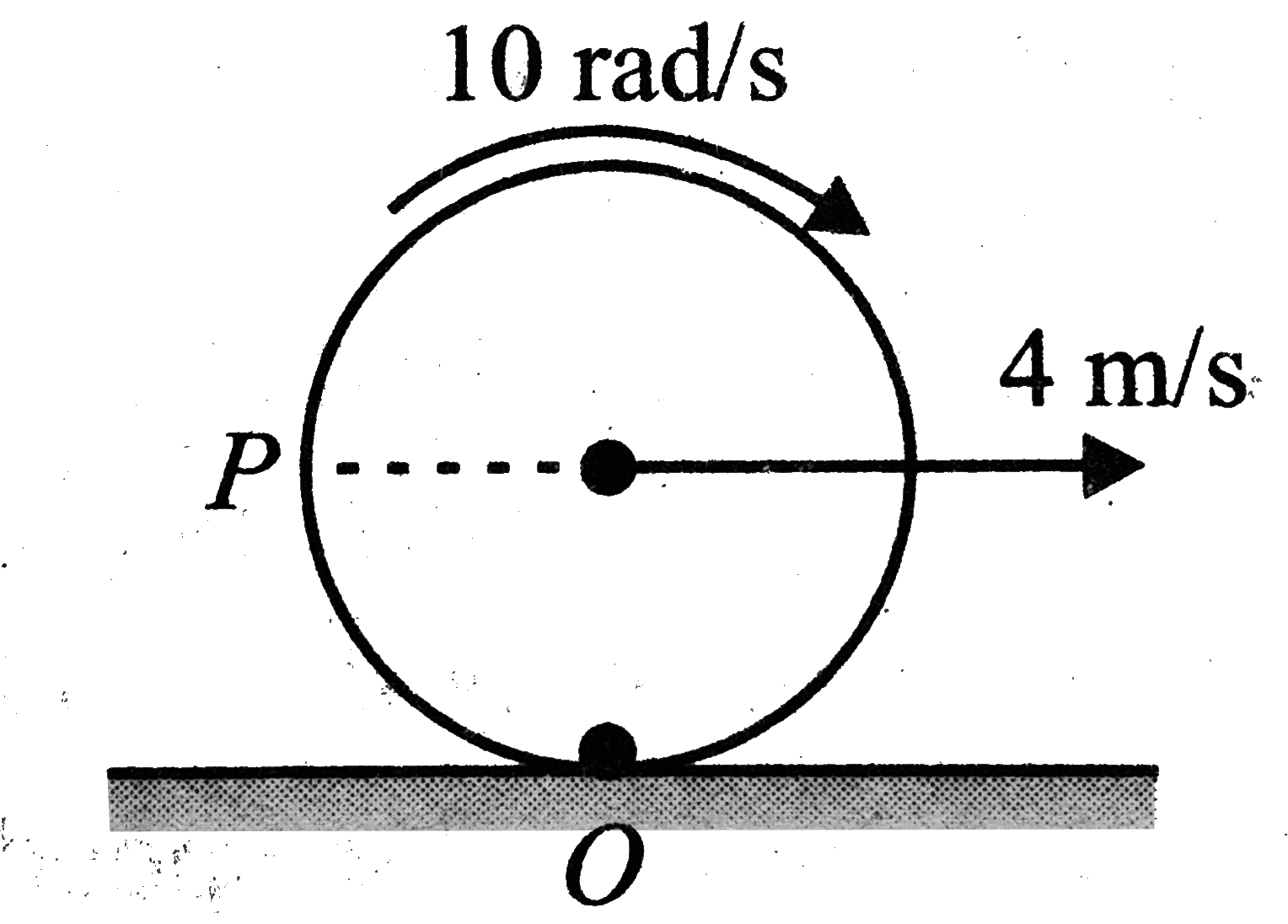
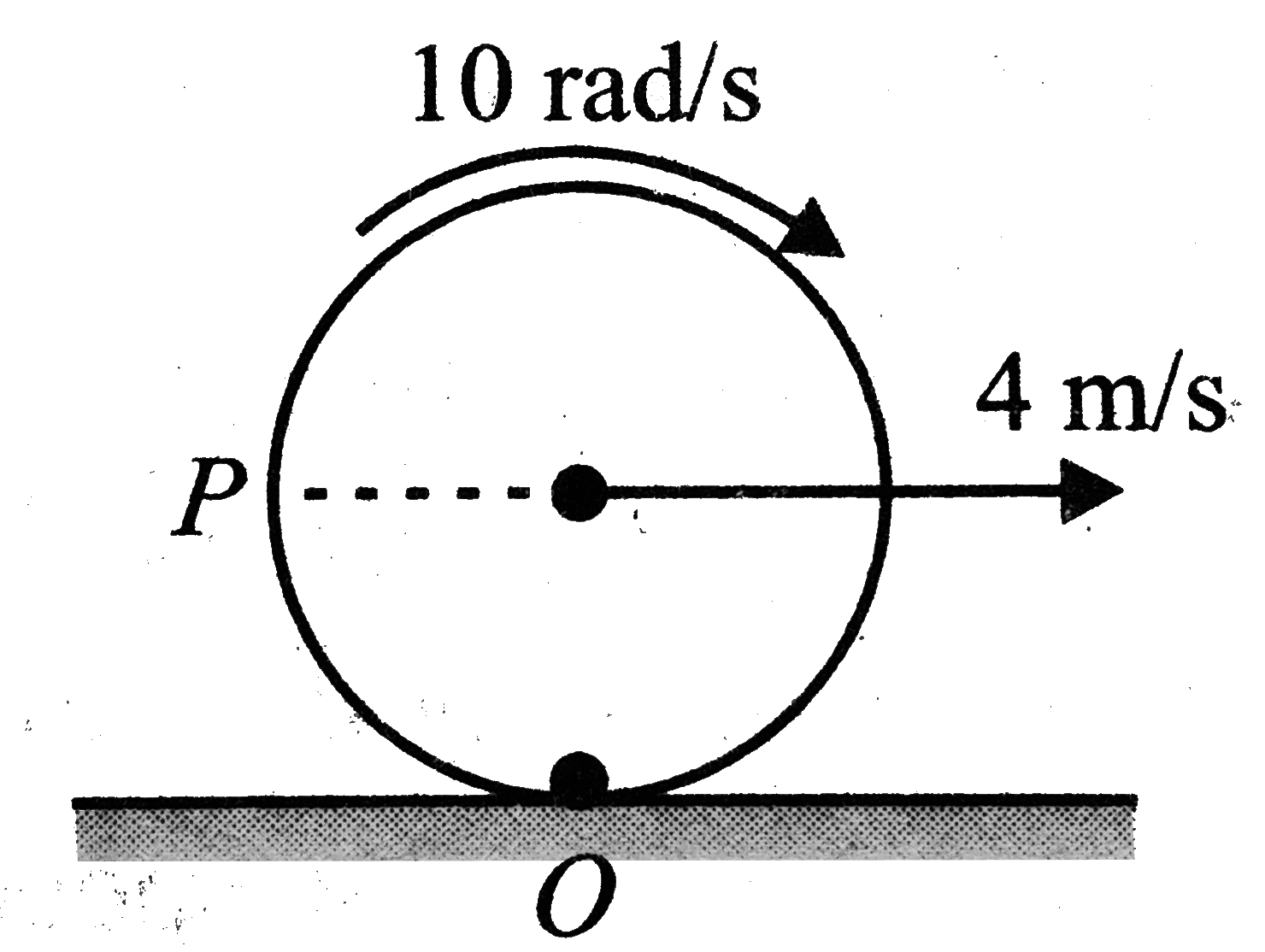
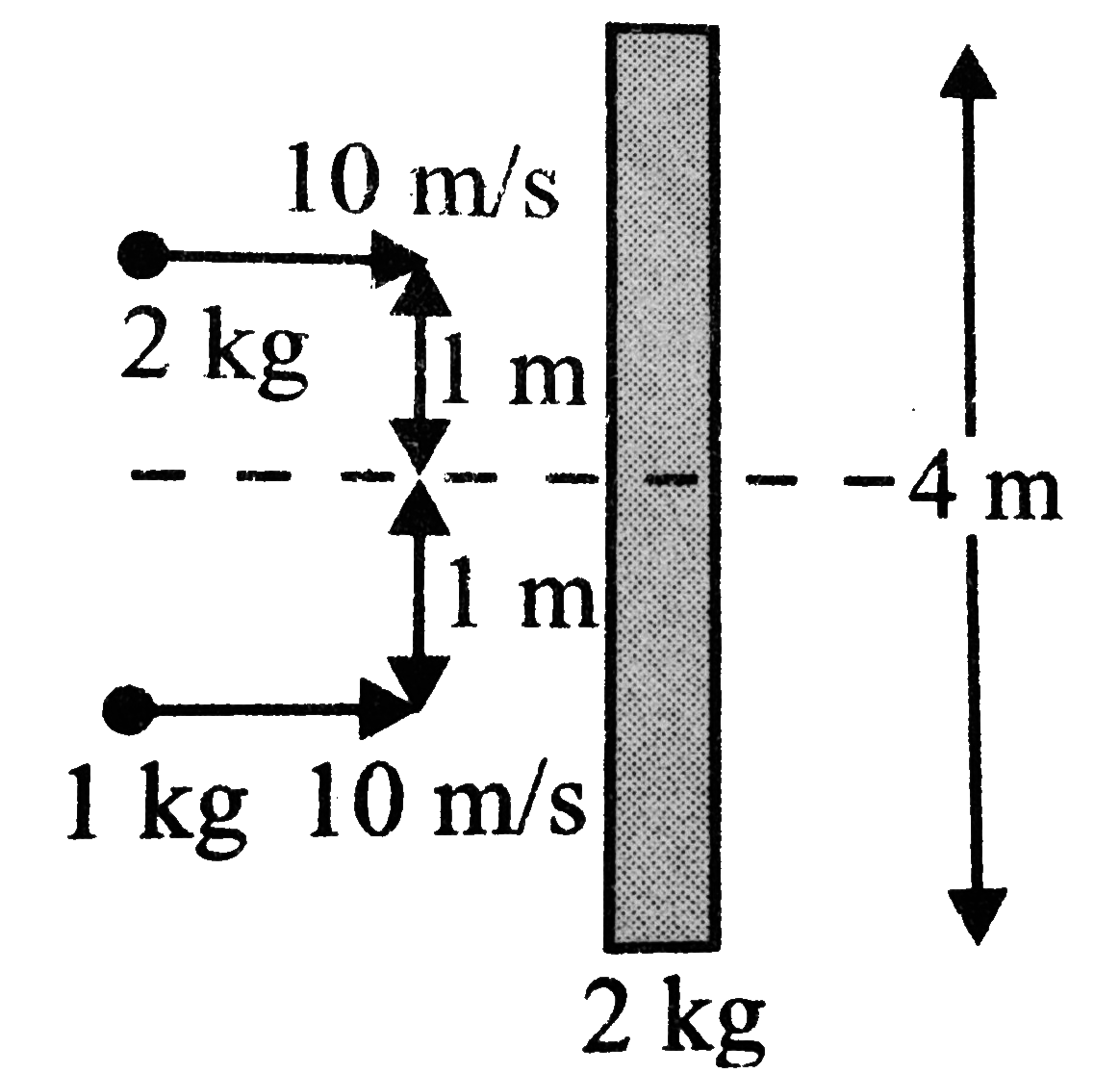
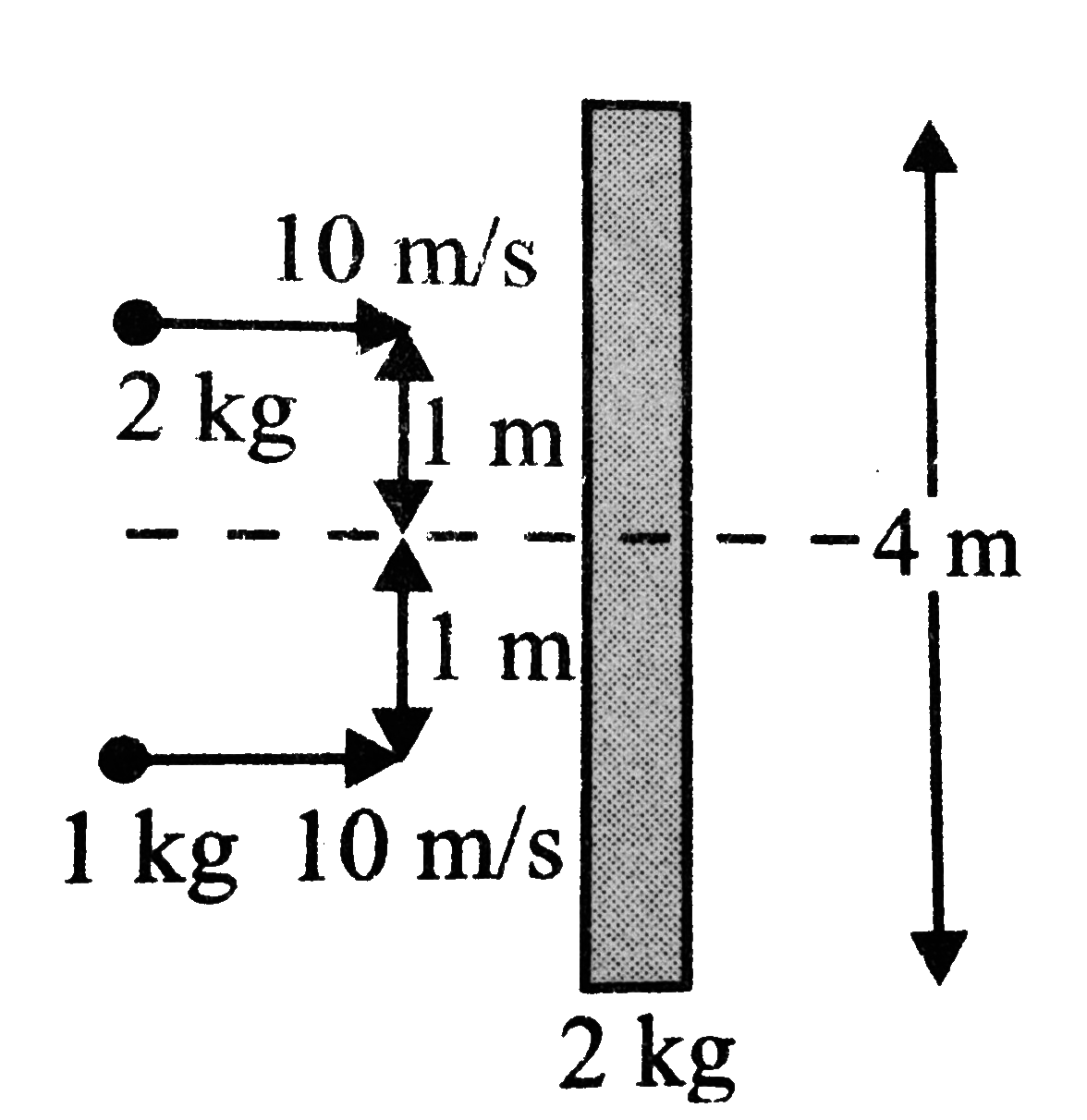
A man of mass 100kg stands at the rim of a turtable of radius 2m and moment of inertia 4000kgm2 mounted on a vertical frictionless shaft at its centre. The whole system is initially at rest. The man now walks along the outer edge of the turntable with a velocity of 1m/s relative to the earth
a. With what angular velocity and in what direction does the turntable rotate?
b. Through what angle will it have rotated when the man reaches his initial position on the turntable?
c. Through what angle will it have rotated when the man reaches his initial position relative to the earth?View SolutionQuestion 2
A small block of mass 4kg is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius 0.5m about the hole with a tangential velocity of 4m/s. The cord is then pulled slowly from below, shorteing the radius of the circle in which the block revolves. The breaking strength of the cord is 600N. What will be radius of the circle when the cord breaks?
 View Solution
View SolutionQuestion 3
A small block of mass 4kg is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius of 5m about the hole, with a tangential velocity of 4m/s. The cord is then pulled slowly from below, shortening the radius of the circle in which the block revolves. The breaking strength of the cord is 200N.
Velocity of the block at the time of breaking of the string View SolutionQuestion 5
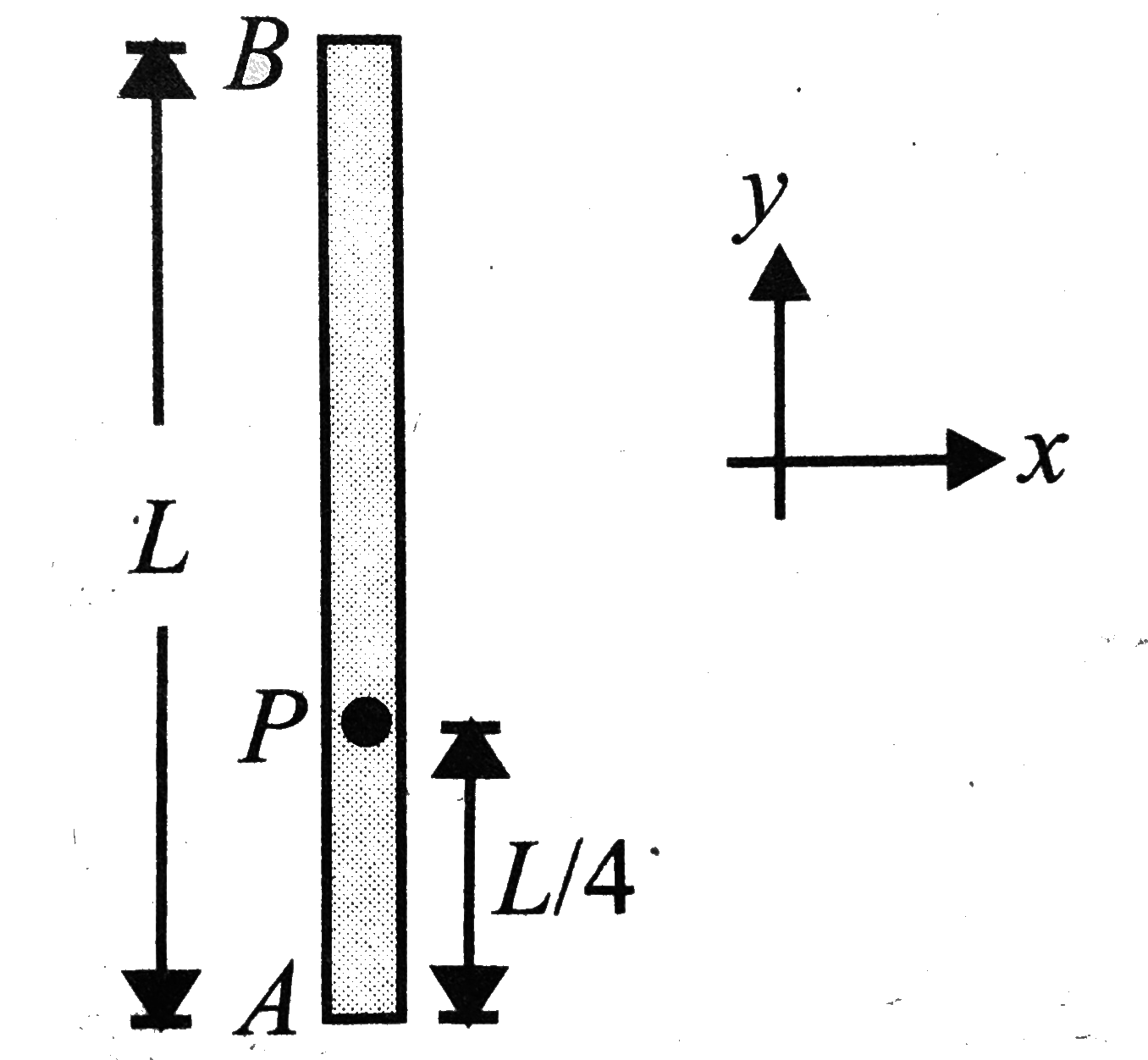
A uniform rod of length l and mass 2m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with initial velocity v collides with one end of the rod and sticks to it.
Determine the position of the point on the rod which remains stationary immediately after collision. View SolutionQuestion 7
A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
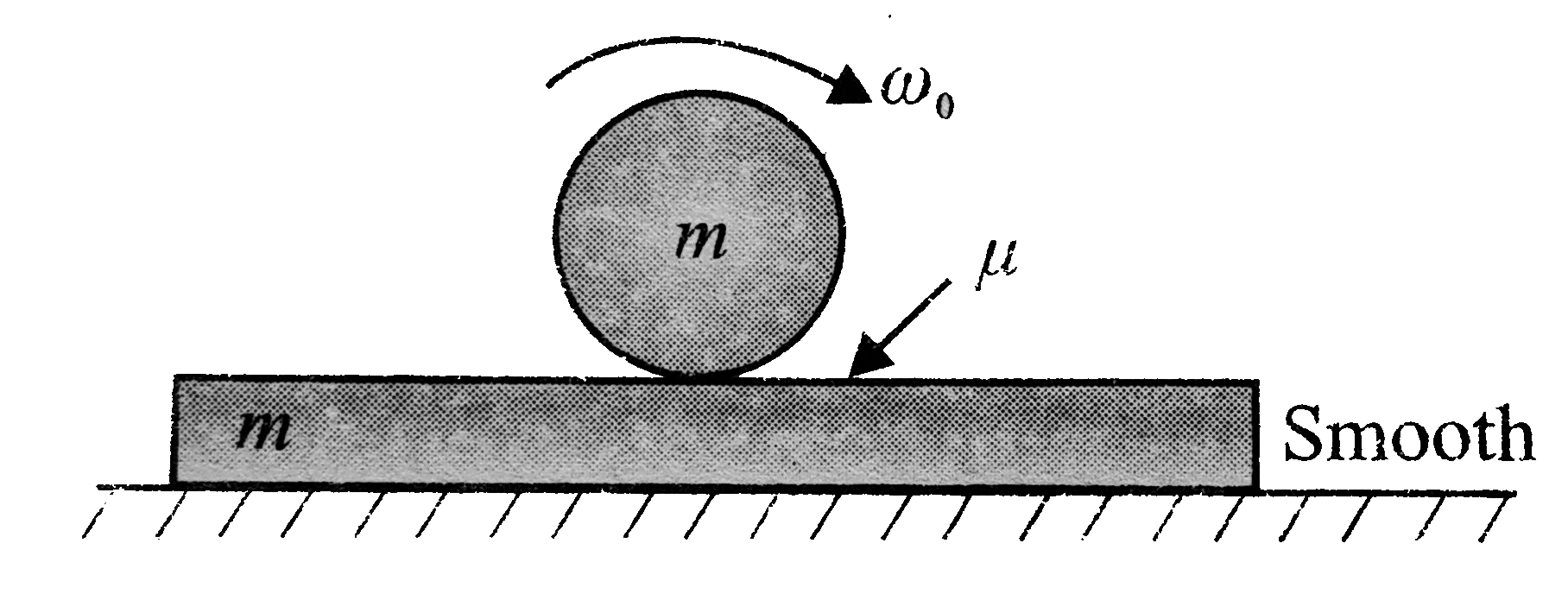
Find the time t at which the pure roiling startsView SolutionQuestion 8
A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity ω0 and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the time t at which the pure roiling startsView SolutionQuestion 9
A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.View SolutionQuestion 10
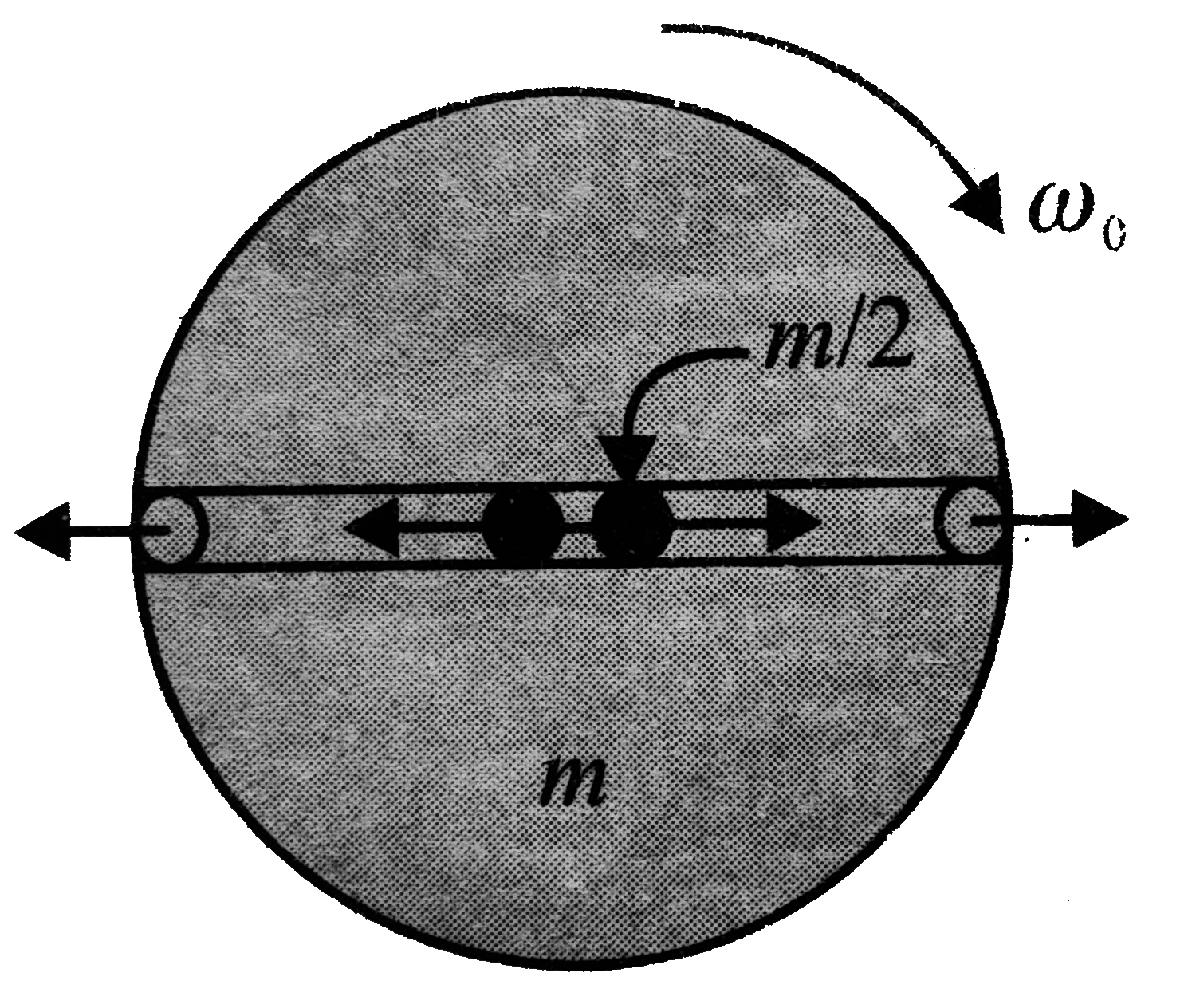
A disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The angular speed of the disc when the balls reach the end of the disc is View SolutionQuestion 11
A disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The speed of each ball relative to the ground just after they leave the disc is
 View Solution
View SolutionQuestion 12
A disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The angular speed of the disc when the balls reach the end of the disc is View SolutionQuestion 13
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision. View SolutionQuestion 14
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the particle with respect to C before the collisionView SolutionQuestion 15
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the particle with respect to C before the collisionView SolutionQuestion 16
A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find (a). the velocity of the centre of the rod and (b). the angular velocity of the rod abut its centre just after the collision. View SolutionQuestion 17
A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find (a). the velocity of the centre of the rod and (b). the angular velocity of the rod abut its centre just after the collision. View SolutionQuestion 18
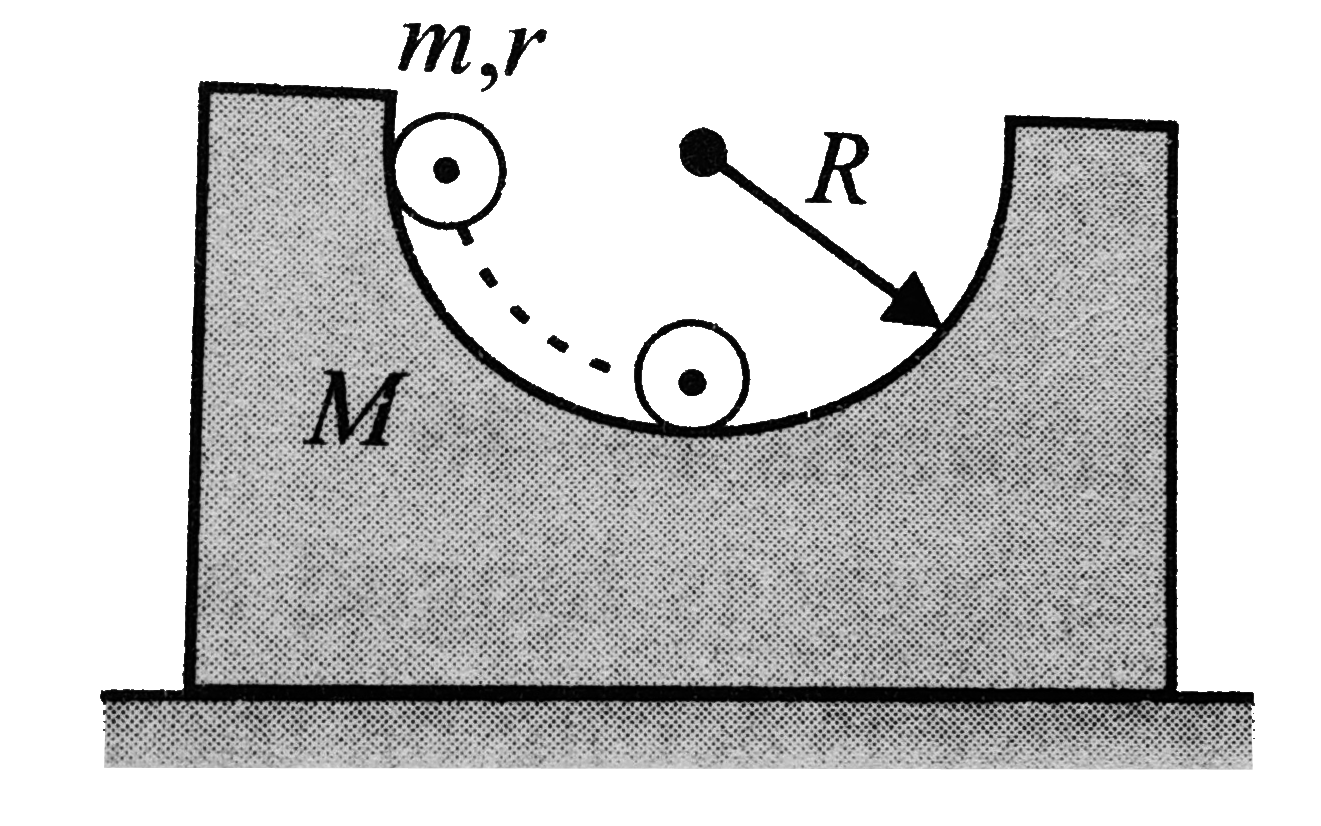
A uniform solid cylinder of mass 2kg and radius 0.2m is released from rest at the top of a semicircular track of radius 0.7m cut in a block of mass M=3kg as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions:

The distance moved by the block when the cylinder reaches the bottom of the track is View SolutionQuestion 19
A uniform solid cylinder of mass 2kg and radius 0.2m is released from rest at the top of a semicircular track of radius 0.7m cut in a block of mass M=3kg as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions:

The distance moved by the block when the cylinder reaches the bottom of the track is View SolutionQuestion 20
A uniform solid cylinder of mass 2kg and radius 0.2m is released from rest at the top of a semicircular track of radius 0.7m cut in a block of mass M=3kg as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions:
The speed of the point of contact of the cylinder with the block w.r.t. ground, when the cylinder reaches the bottom of the track is View SolutionQuestion 21
A disc of a mass M and radius R can rotate freely in vertical plane about a horizontal axis at O. Distant r from the center of disc as shown in the figure. The disc is released from rest in the shown position.

The angular acceleration of disc when OC rotates by an angles of 37∘ is View SolutionQuestion 24
In the given figure F=10N , R=1 m , mass of the body is 2 kg and moment of inertia of the body about an axis passing through O and perpendicular to plane of body is 4kg−m2 .O is the centre of mass of the body.

If the ground is smooth , what is total kinetic energy of the body after 2 s?View SolutionQuestion 25
In the given figure F=10N , R=1 m , mass of the body is 2 kg and moment of inertia of the body about an axis passing through O and perpendicular to plane of body is 4kg−m2 .O is the centre of mass of the body.

If ground is sufficiently rough , what is kinetic energy of the body now in the given time interval ?View SolutionQuestion 34
A uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having velocity of 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. ThenView SolutionQuestion 35
A uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having velocity of 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. ThenView SolutionQuestion 36
When a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
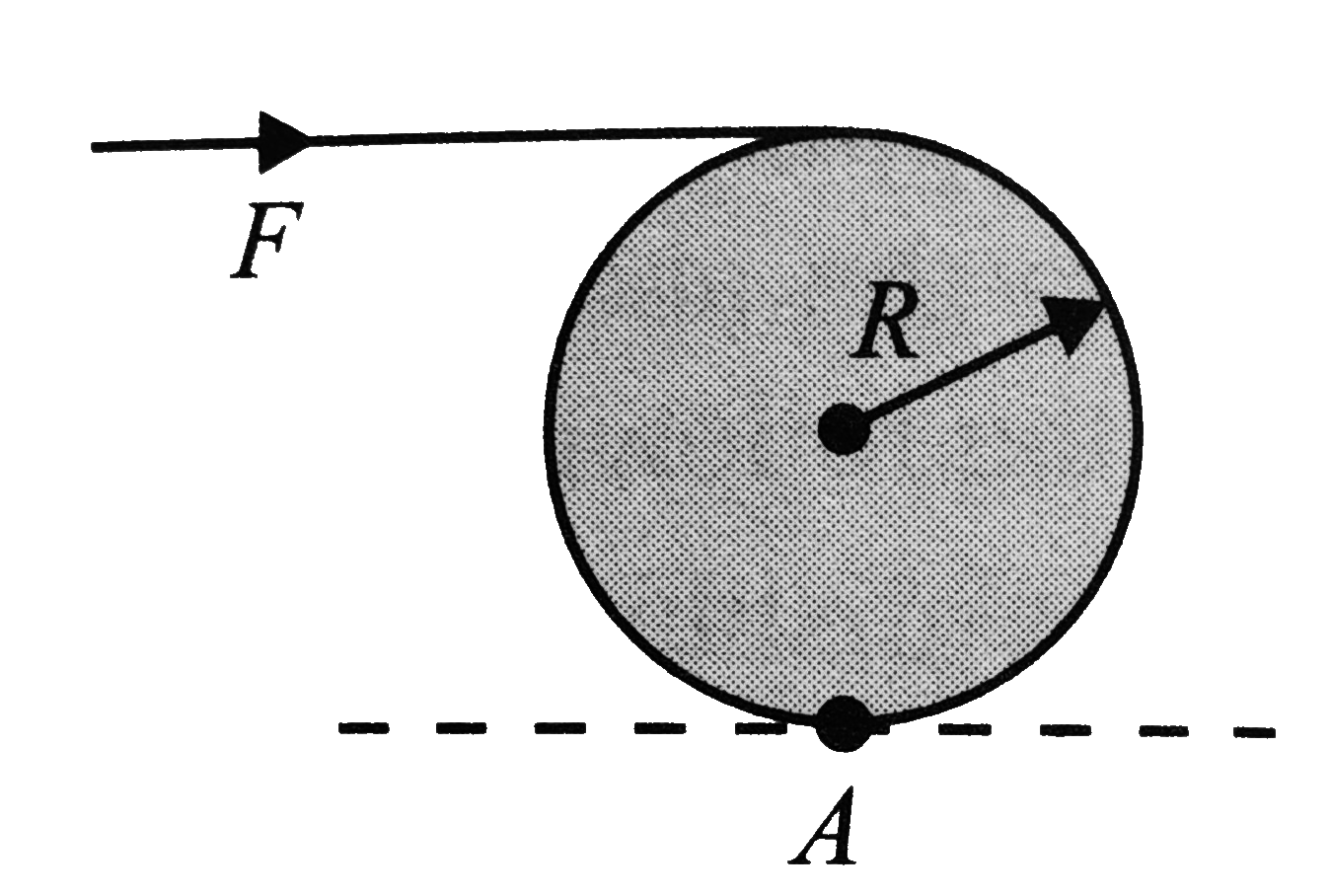
Tangential acceleration of the centre of mass is View SolutionQuestion 37
When a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
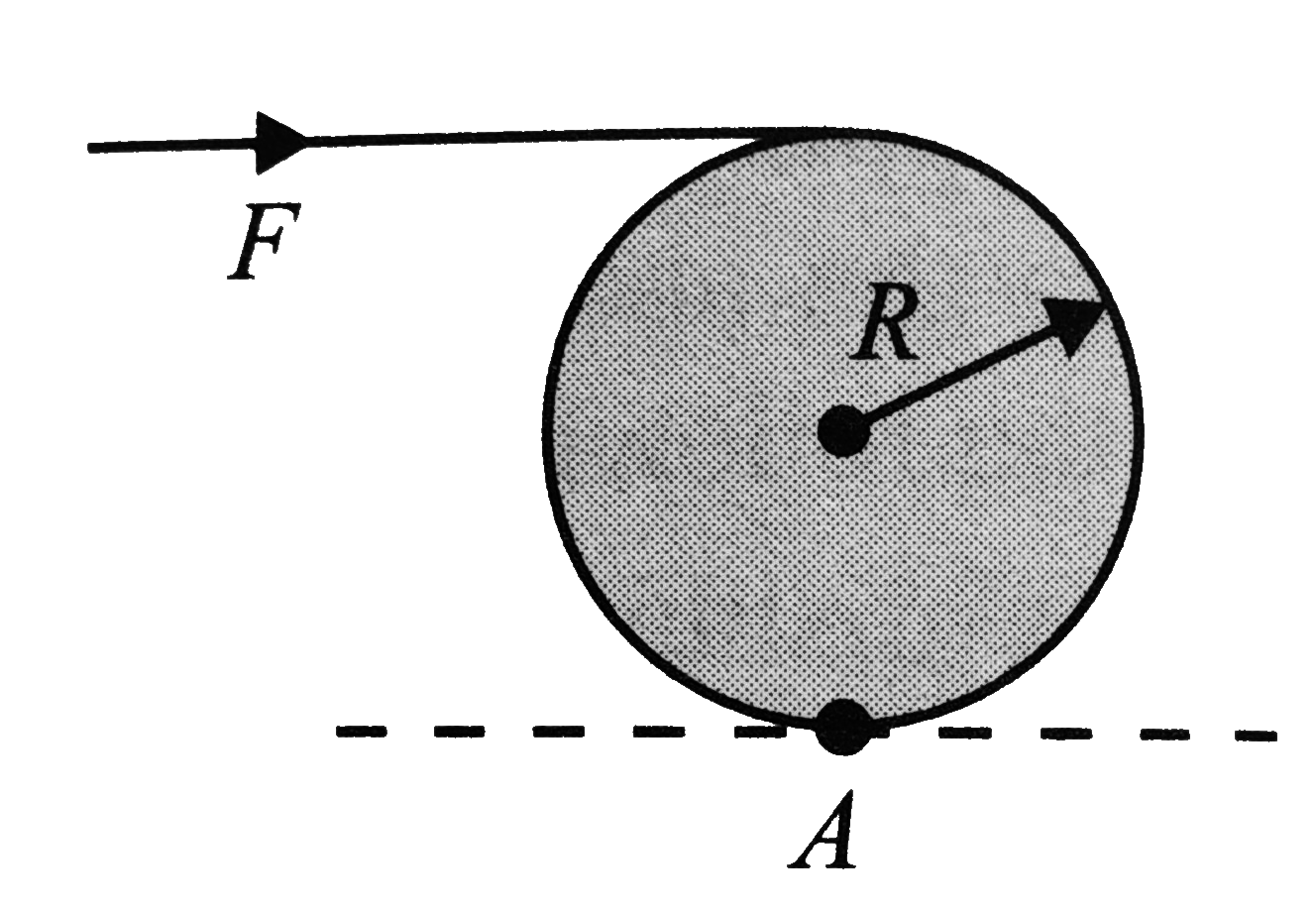
Component of reaction at the hinge in the vertical direction is View SolutionQuestion 38
When a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
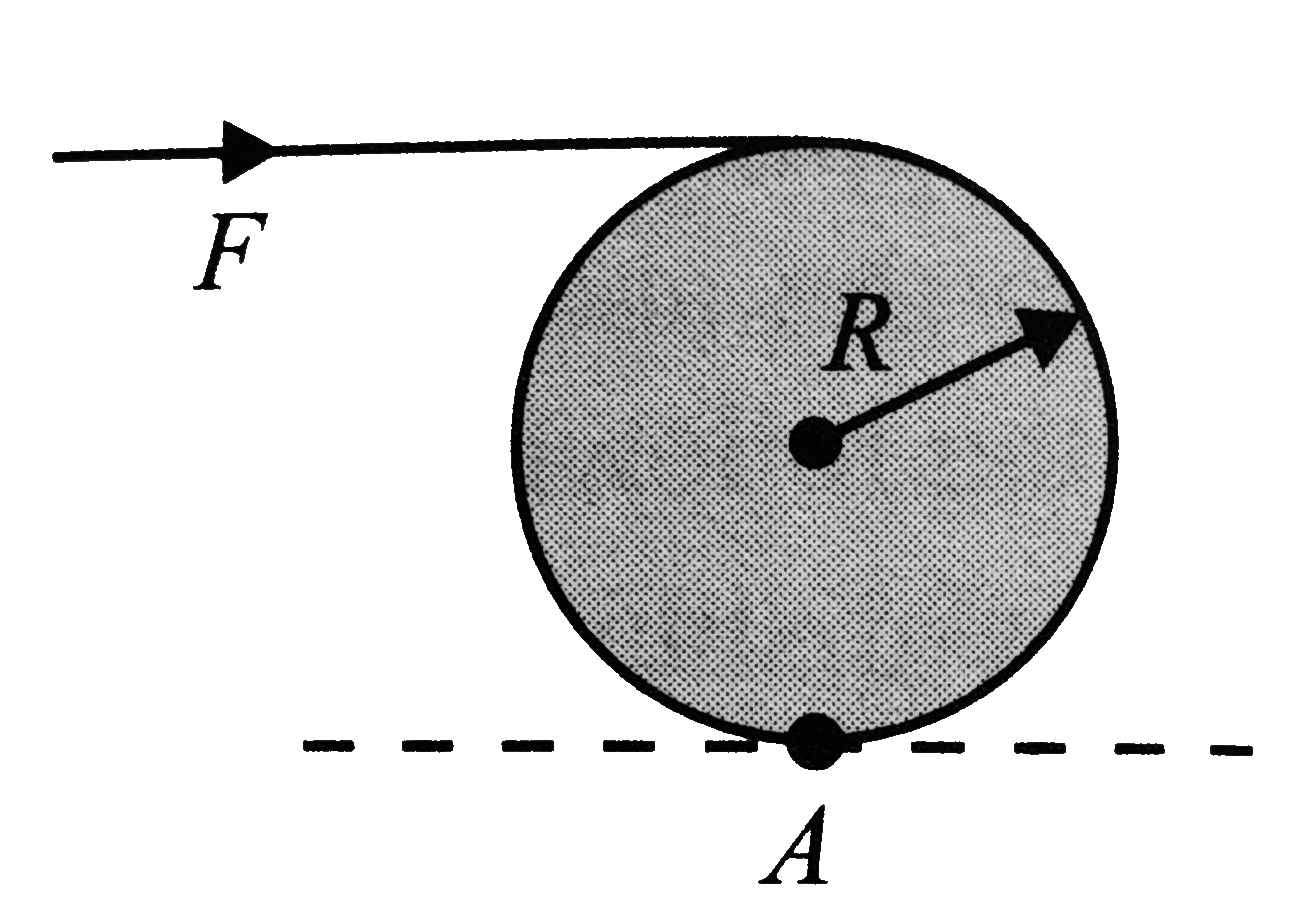
Component of reaction at the hinge in the horizontal direction is View SolutionQuestion 39
A rod AB of mass M and length 8l lies on a smooth horizontal surface. A particle, of mass m and velocity v0 strike's the rod perpendicular to its length, as shown in Fig. As a result of the collision, the centre of mass of the rod attains a speed of v0/8 and the particle rebounds back with a speed of v0/4. Find the following: a. The ratio M/m. b. The angular velocity of the rod about O. c. The coefficient of restitution 'e' for the collision. d. The velocities of the ends 'A' and 'B' of the rod, namely, vA and vB respectively.
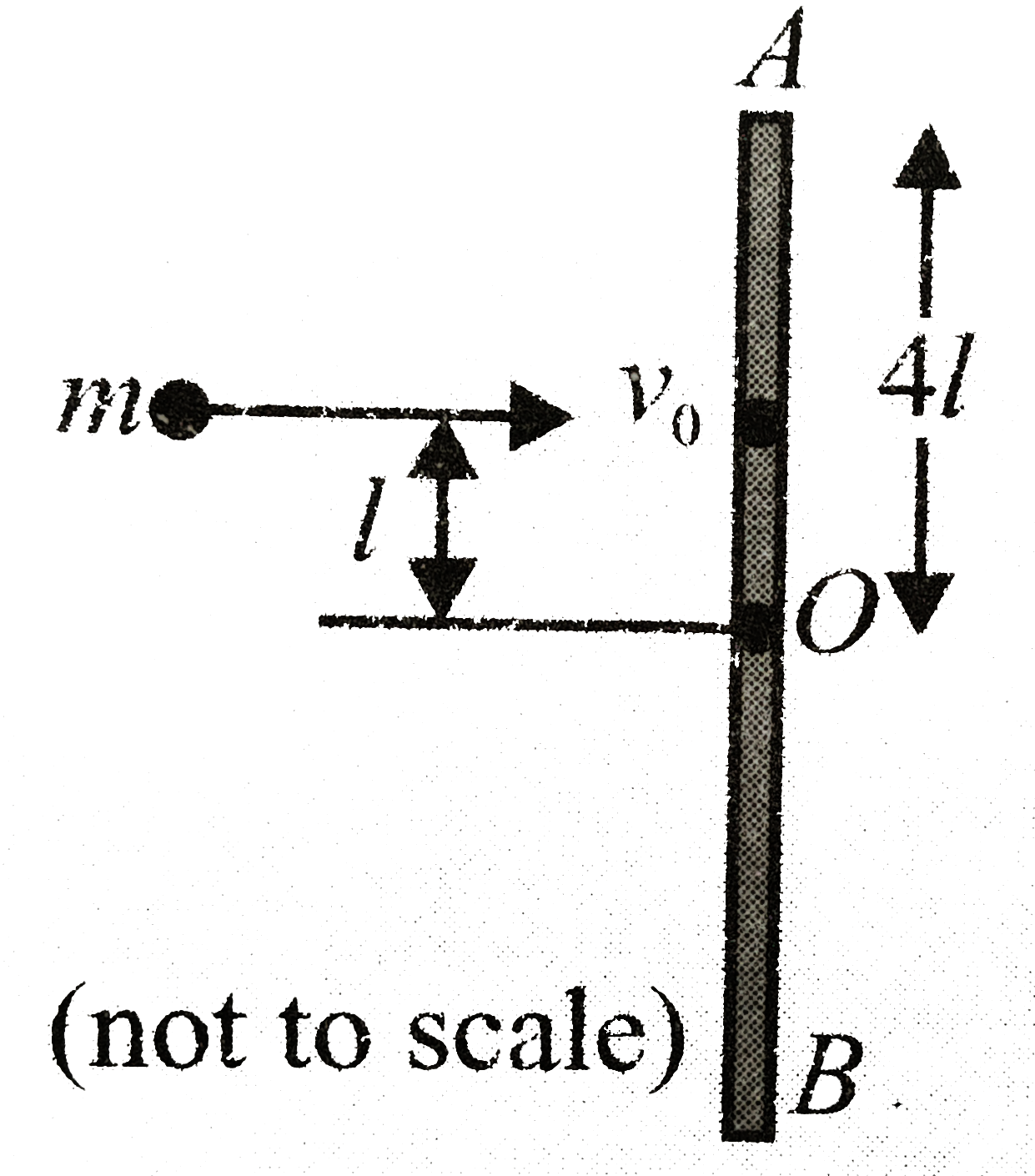 View Solution
View SolutionQuestion 40
A rod AB of mass M and length 8l lies on a smooth horizontal surface. A particle, of mass m and velocity v0 strike's the rod perpendicular to its length, as shown in Fig. As a result of the collision, the centre of mass of the rod attains a speed of v0/8 and the particle rebounds back with a speed of v0/4. Find the following: a. The ratio M/m. b. The angular velocity of the rod about O. c. The coefficient of restitution 'e' for the collision. d. The velocities of the ends 'A' and 'B' of the rod, namely, vA and vB respectively.
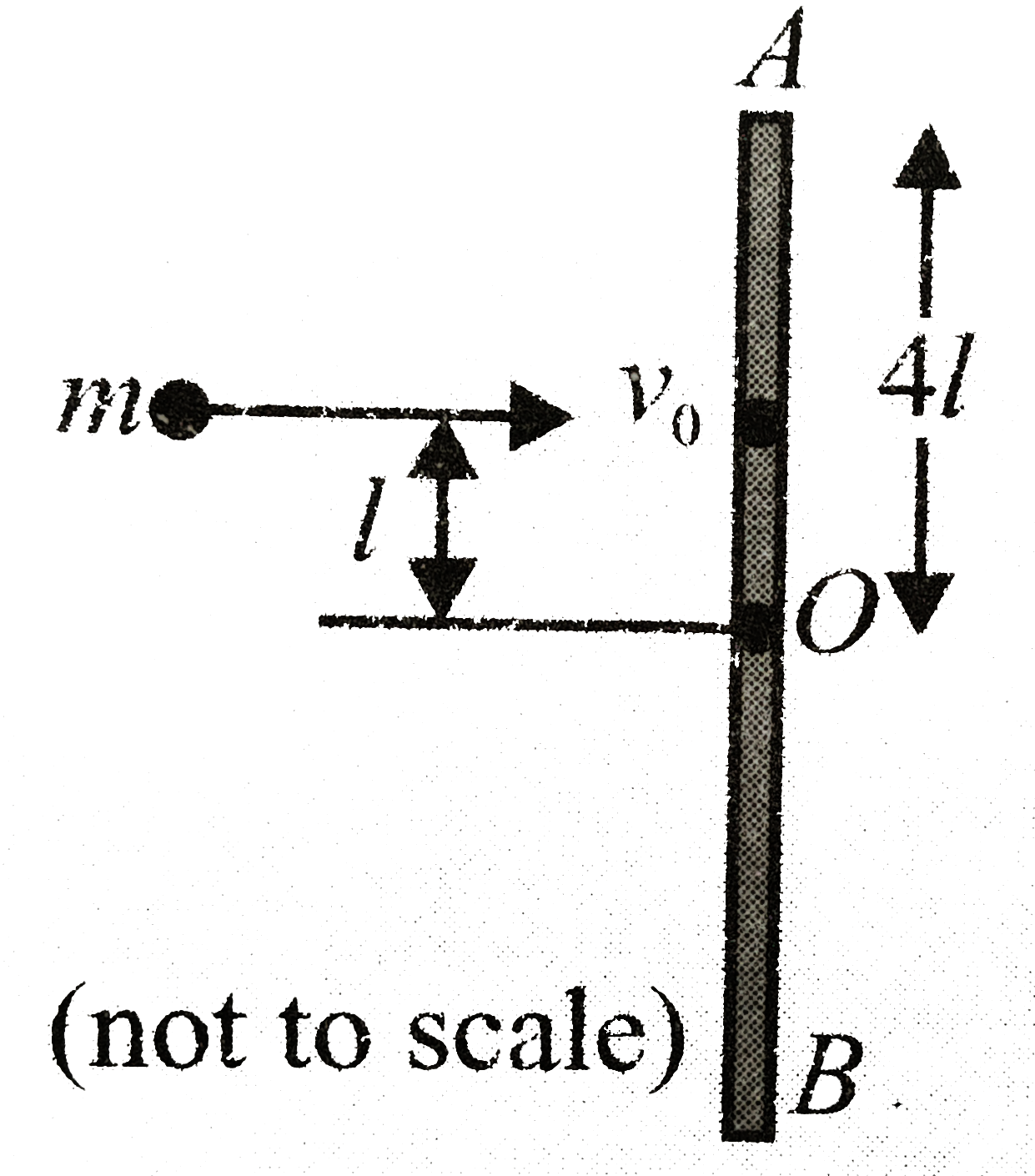 View Solution
View SolutionQuestion 41
A rod AB of mass M and length 8l lies on a smooth horizontal surface. A particle, of mass m and velocity v0 strike's the rod perpendicular to its length, as shown in Fig. As a result of the collision, the centre of mass of the rod attains a speed of v0/8 and the particle rebounds back with a speed of v0/4. Find the following: a. The ratio M/m. b. The angular velocity of the rod about O. c. The coefficient of restitution 'e' for the collision. d. The velocities of the ends 'A' and 'B' of the rod, namely, vA and vB respectively.
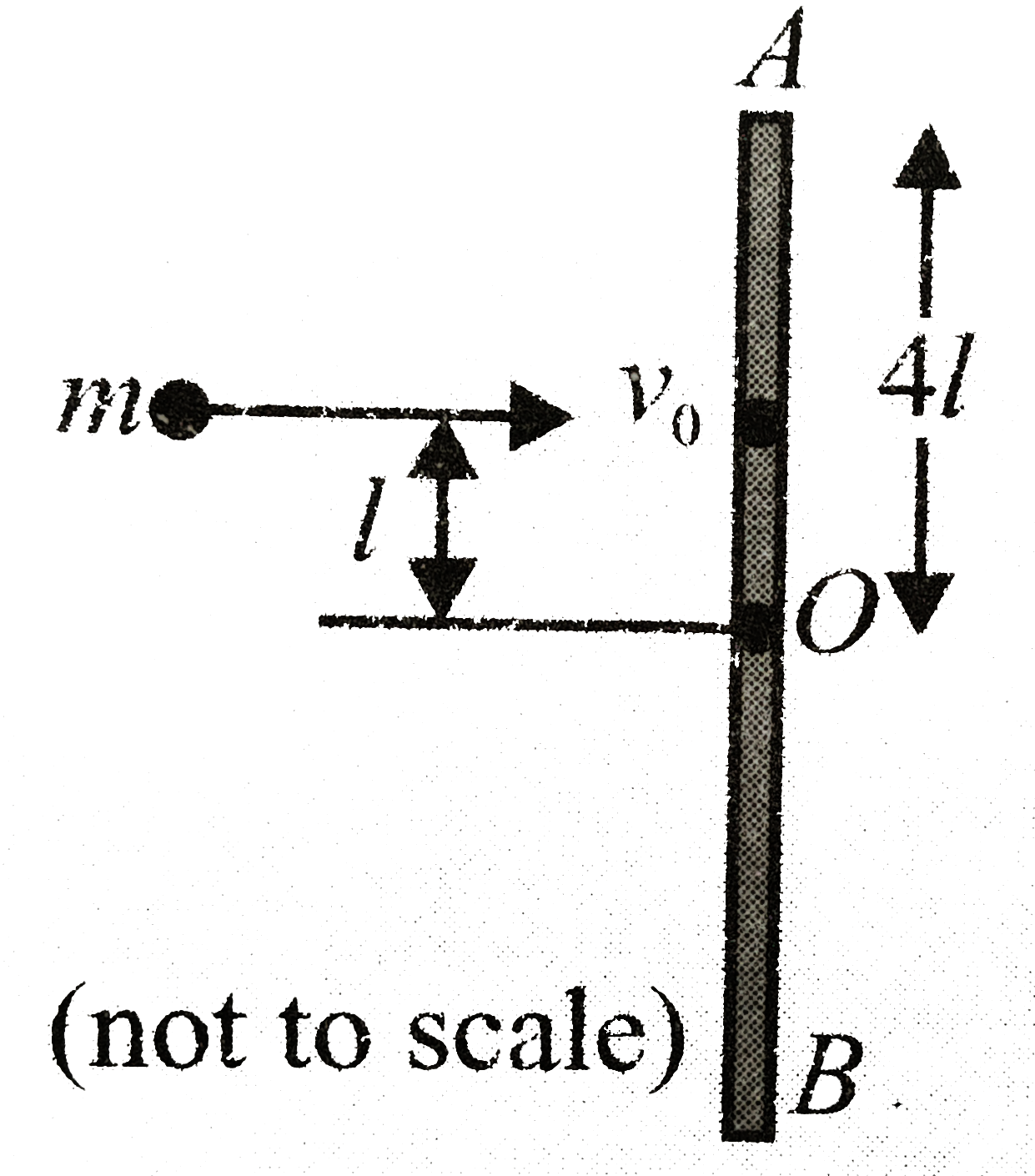 View Solution
View SolutionQuestion 42
A rod AB of mass M and length 8l lies on a smooth horizontal surface. A particle, of mass m and velocity v0 strike's the rod perpendicular to its length, as shown in Fig. As a result of the collision, the centre of mass of the rod attains a speed of v0/8 and the particle rebounds back with a speed of v0/4. Find the following: a. The ratio M/m. b. The angular velocity of the rod about O. c. The coefficient of restitution 'e' for the collision. d. The velocities of the ends 'A' and 'B' of the rod, namely, vA and vB respectively.
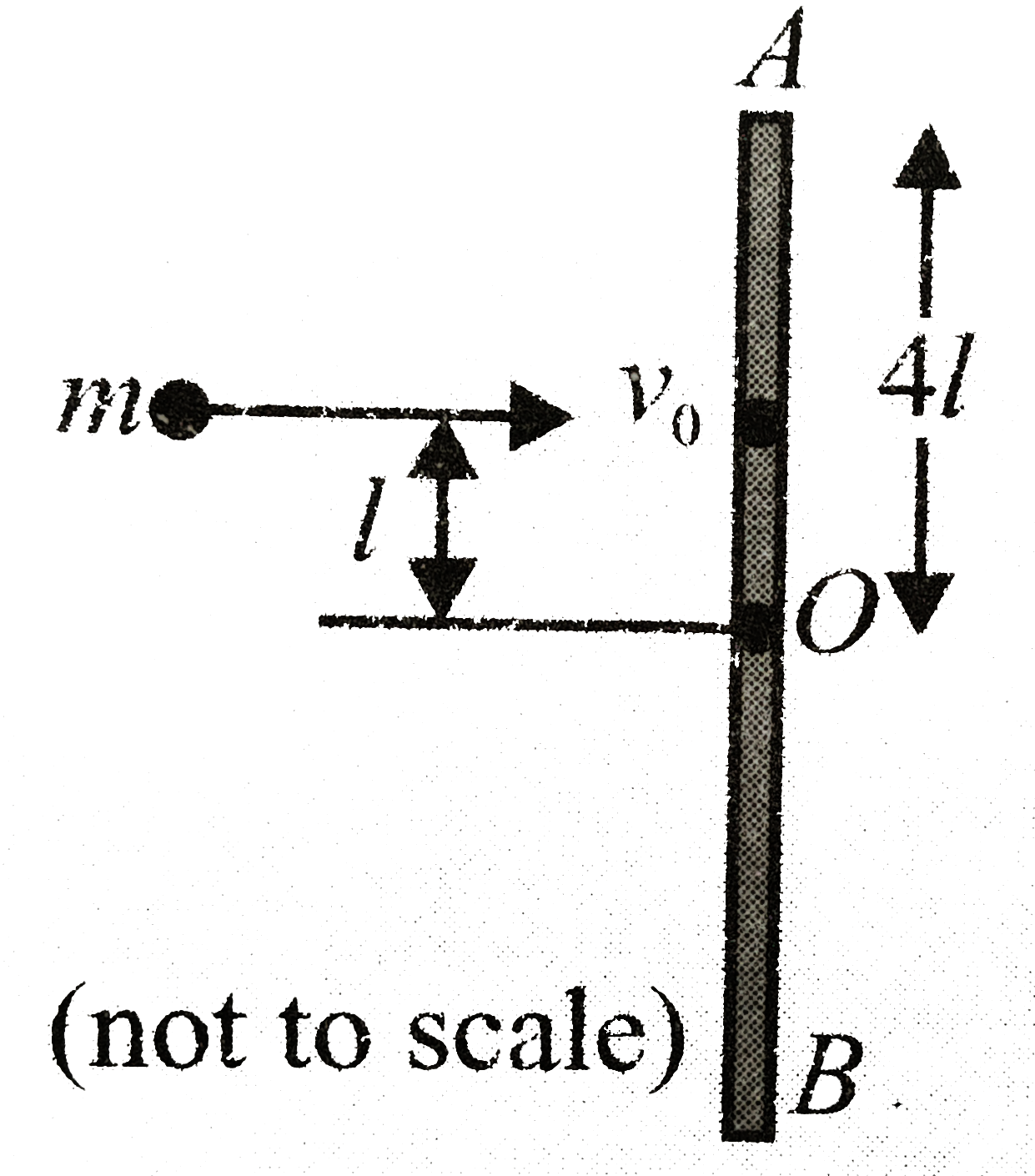 View Solution
View SolutionQuestion 46
A spherical ball of mass M moving with initial velocity V collides elastically with another ball of mass M, which is fixed at one end of L shaped rigid massless frame as shown in Fig. (a). The L shaped frame contains another mass M connected at the other end.
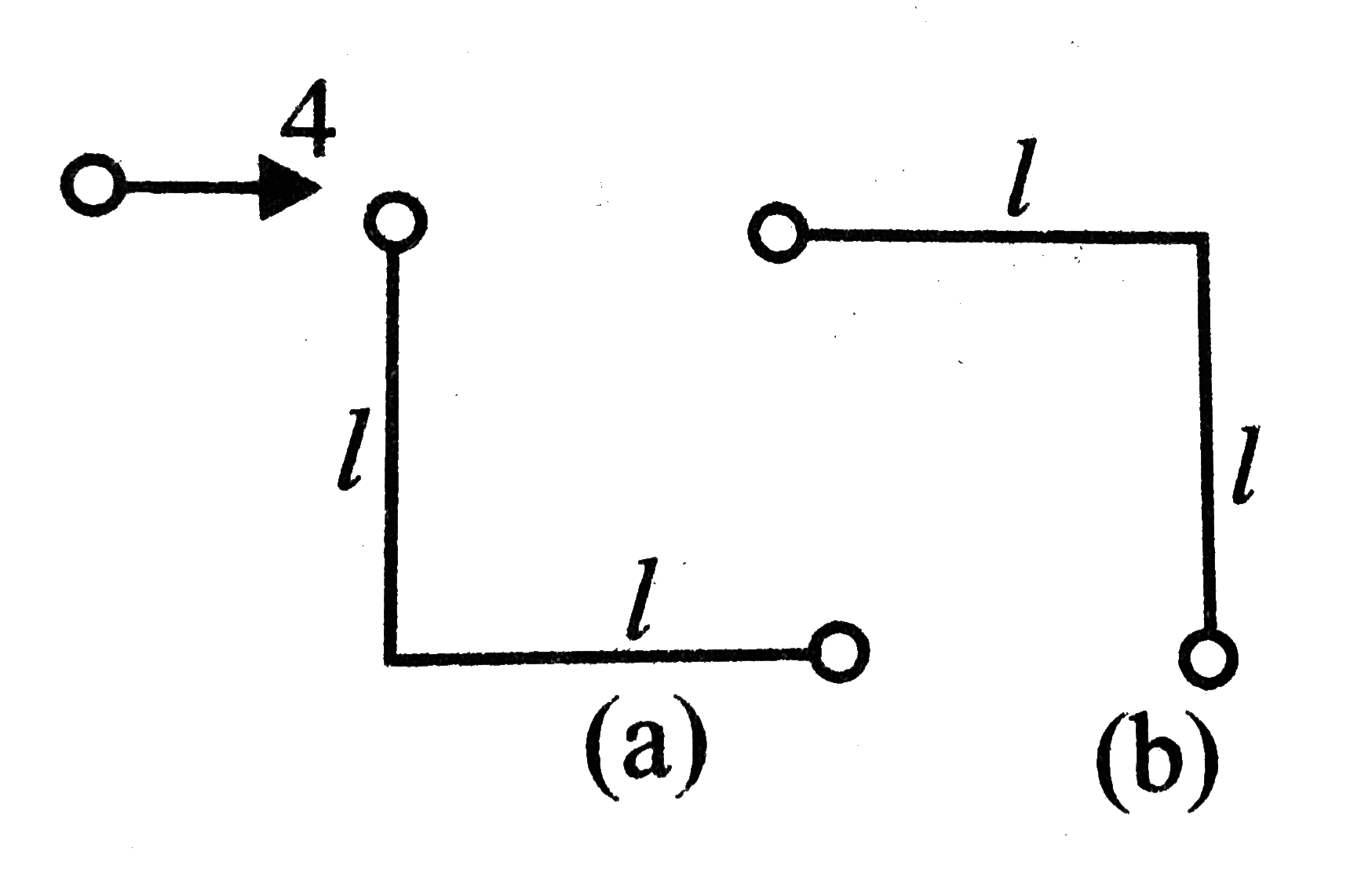
The speed of the striking mass after collision is View SolutionQuestion 47
A spherical ball of mass M moving with initial velocity u collides elastically with another ball of mass M, which is fixed at one end of L shaped rigid massless frame as shown in Fig. (a). The L shaped frame contains another mass M connected at the other end.

The speed of the striking mass after collision is View SolutionQuestion 48
A spherical ball of mass M moving with initial velocity u collides elastically with another ball of mass M, which is fixed at one end of L shaped rigid massless frame as shown in Fig. (a). The L shaped frame contains another mass M connected at the other end.

The speed of the striking mass after collision is View SolutionQuestion 50
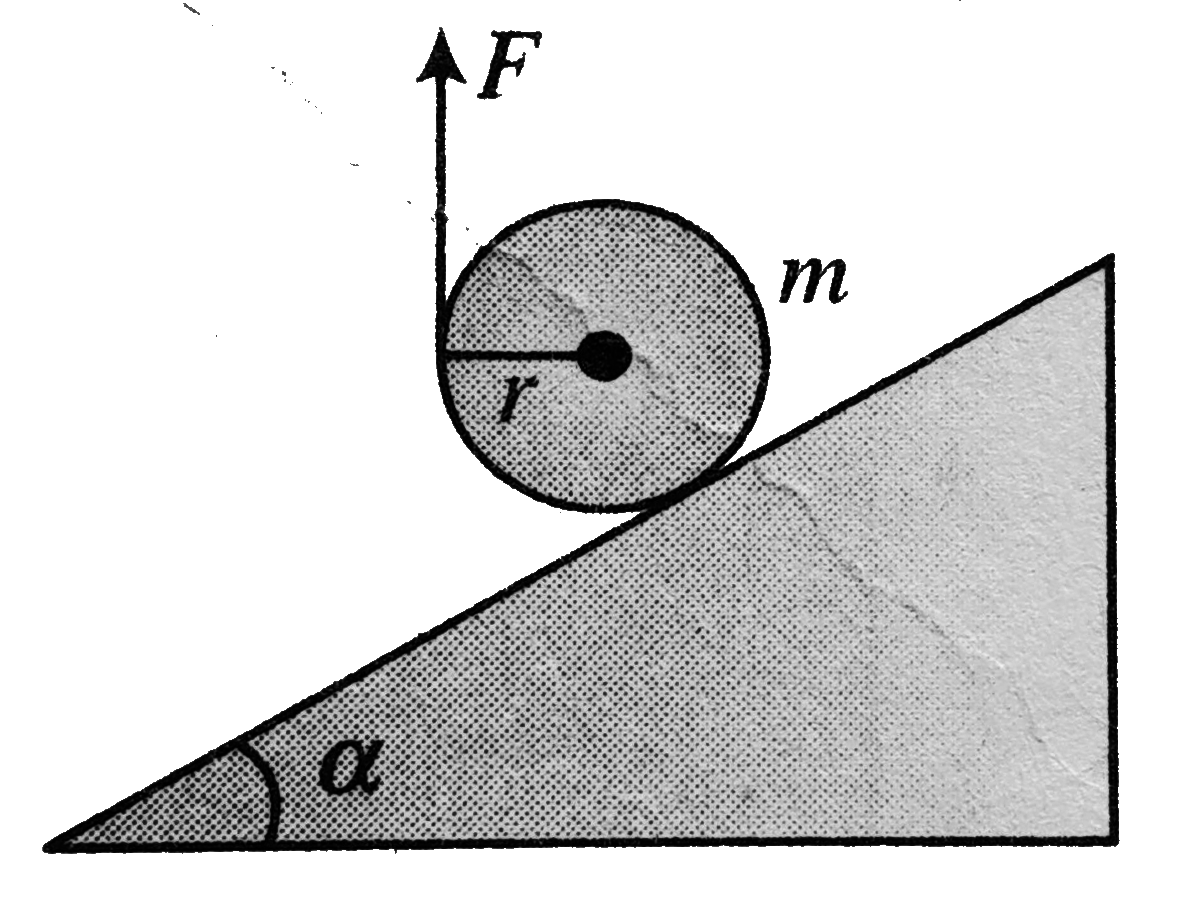
A solid cylinder of mass m is kept in balance on a fixed incline of angle α=37∘ with the help of a thread fastened to its jacket. The cylinder does not slip.

In what direction should the thread be pulled to minimise the force required to hold the cylinder? What is the magnitude of this force?View SolutionQuestion 53
A ball, rolling purely on a horizontal floor with centre's speed v, hits a smooth vertical wall surface elastically. Answer the following questions.
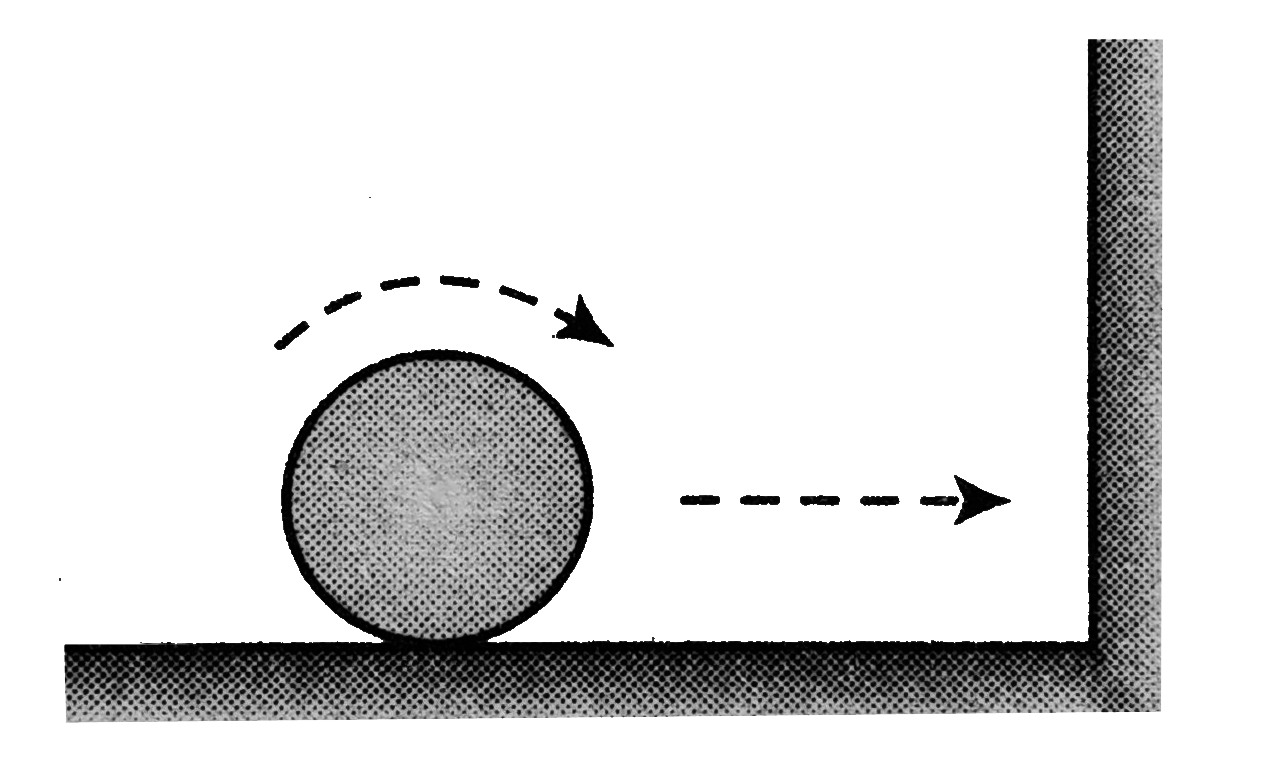
The change in angular momentum of the solid ball (mass m, radius R), about the corner point of floor and wall, due to the collision is View SolutionQuestion 54
A uniform disc of mass 1kg and radius 20cm is rolling purely on a flat horizontal surface. Its centre C is moving with acceleration a=20ms−2 and velocity v=4m/s at a certain instant. At this instant. points A and B are located on the disc as shown in the diagram, with AC=BC=10cm.

What is the kinetic energy of the disc? View SolutionQuestion 55
A uniform disc of mass 1kg and radius 20cm is rolling purely on a flat horizontal surface. Its centre C is moving with acceleration a=20ms−2 and velocity v=4m/s at a certain instant. At this instant. points A and B are located on the disc as shown in the diagram, with AC=BC=10cm.
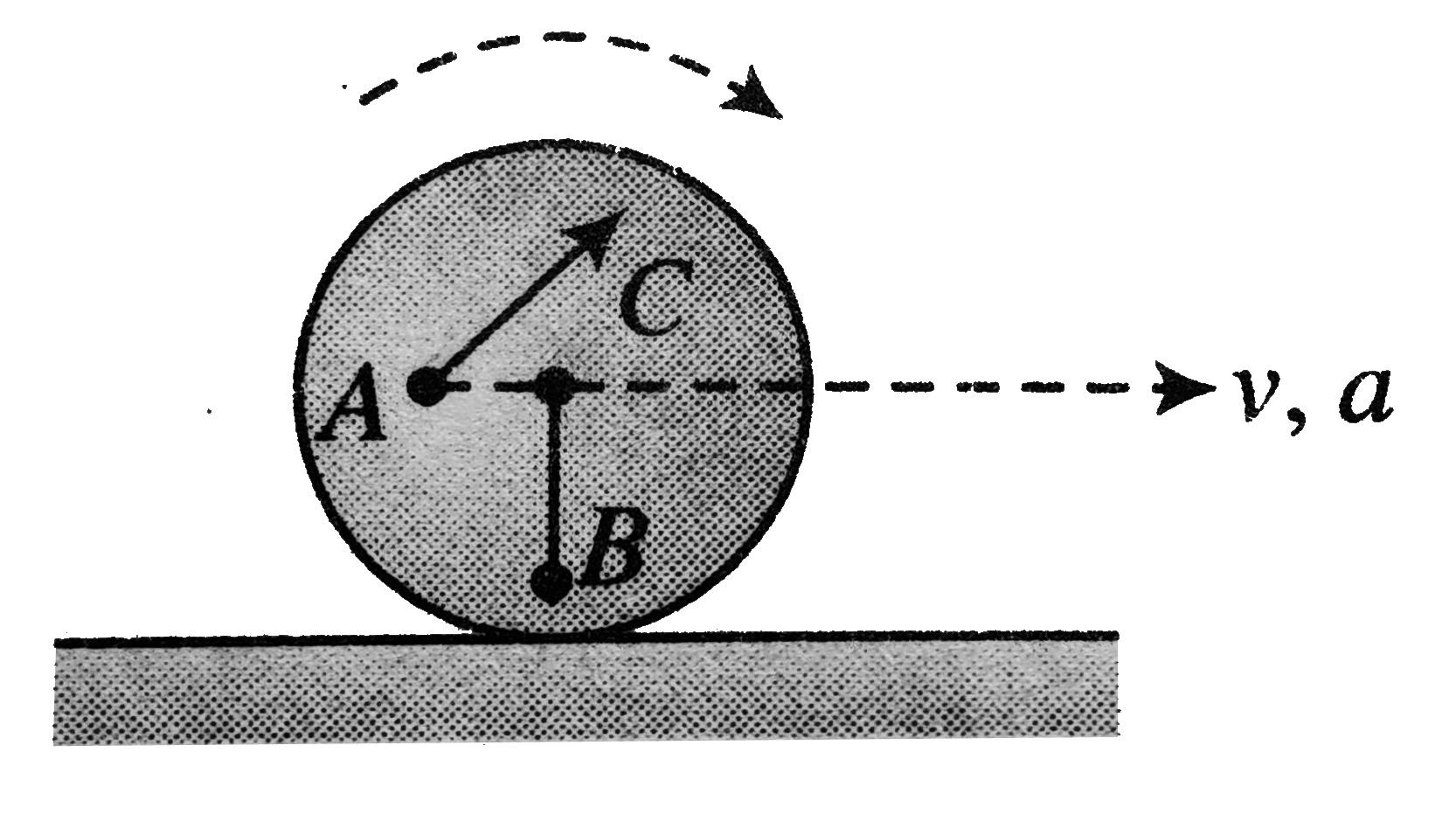
What is the acceleration magnitude of point A? View SolutionQuestion 56
A uniform disc of mass 1kg and radius 20cm is rolling purely on a flat horizontal surface. Its centre C is moving with acceleration a=20ms−2 and velocity v=4m/s at a certain instant. At this instant. points A and B are located on the disc as shown in the diagram, with AC=BC=10cm.

What is the acceleration magnitude of point B? View SolutionQuestion 57
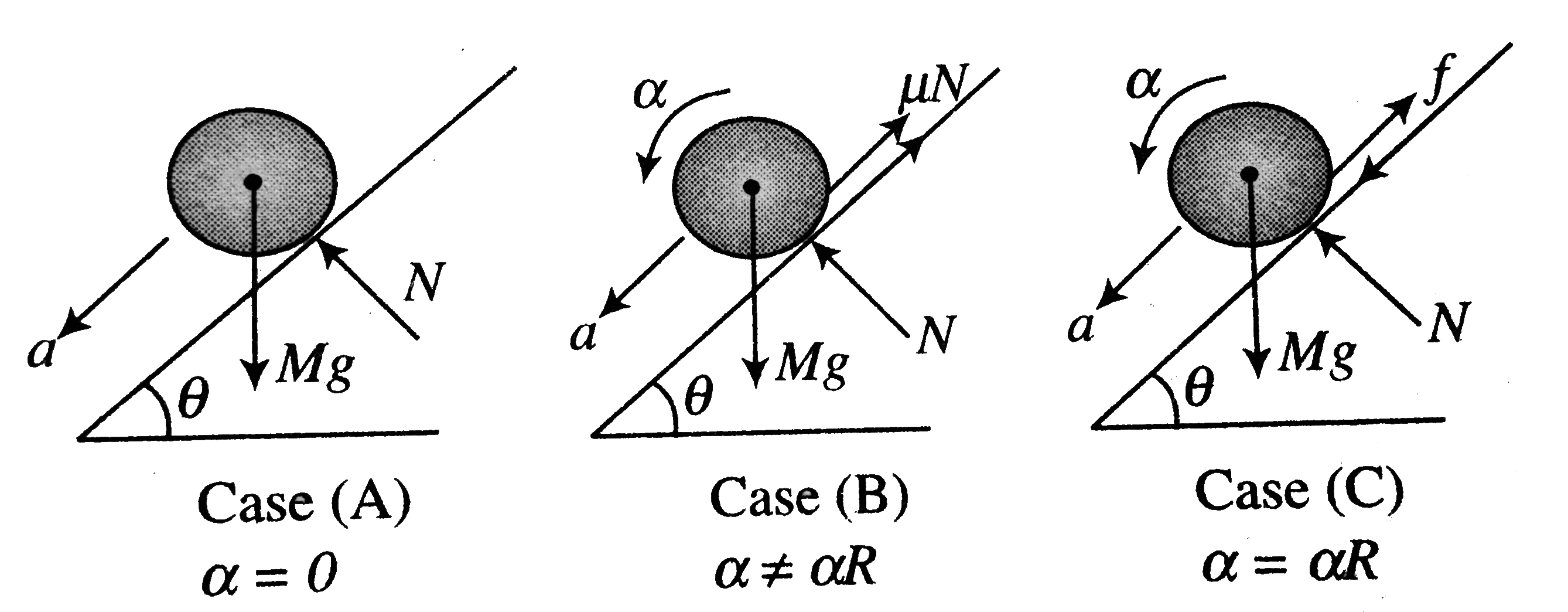
In this passage a brief idea is given of the motion of the rolling bodies on an inclined plane. We will consider three cases: objects are released on an incline plane
Case-A: which is smooth.
Case-B: where friction is insufficient to provide pure rolling.
Case-C: where friction is sufficient to provide pure rolling. Force diagram for three cases are as follows: (where symbols have their usual meanings)
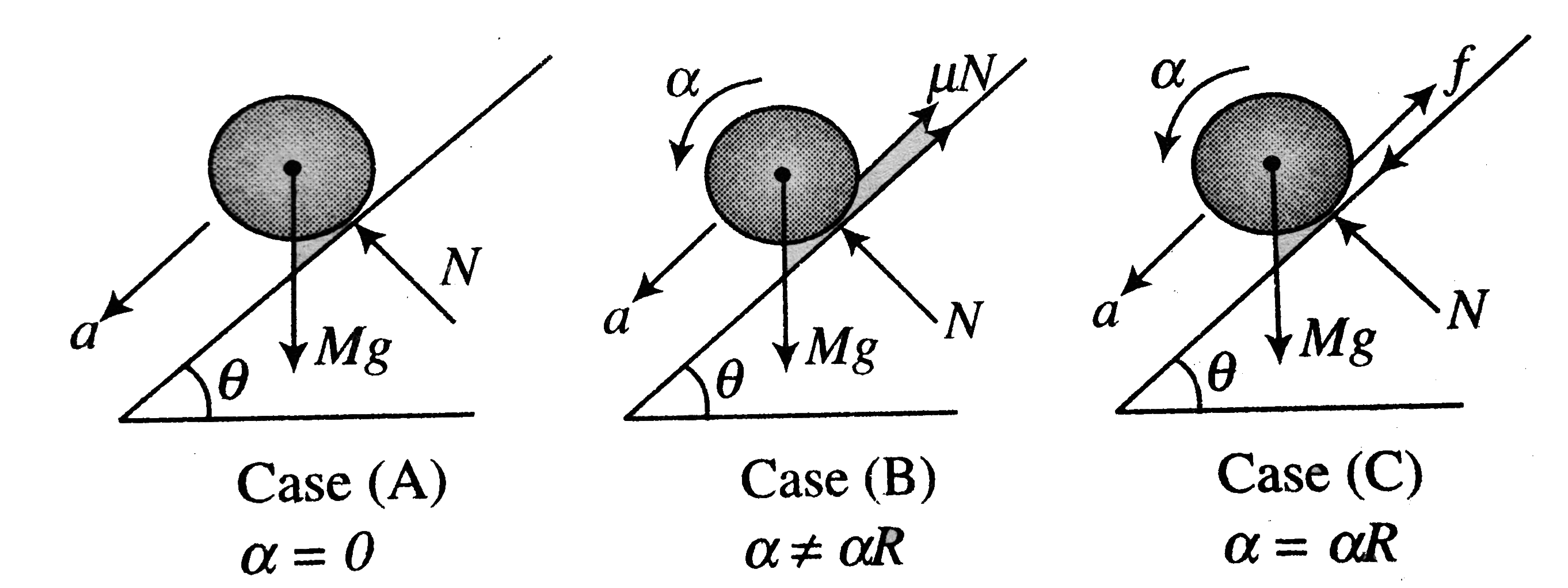
If the four objects given in the above question are of same mass, same radius having the same friction coefficient and are released from the same height, then at the bottom the object which will have least kinetic energy for case B will be the:View SolutionQuestion 58
In this passage a brief idea is given of the motion of the rolling bodies on an inclined plane. We will consider three cases: objects are released on an incline plane
Case-A: which is smooth.
Case-B: where friction is insufficient to provide pure rolling.
Case-C: where friction is sufficient to provide pure rolling. Force diagram for three cases are as follows: (where symbols have their usual meanings)

If the four objects given in the above question are of same mass, same radius having the same friction coefficient and are released from the same height, then at the bottom the object which will have least kinetic energy for case B will be the:View SolutionQuestion 59
In this passage a brief idea is given of the motion of the rolling bodies on an inclined plane. We will consider three cases: objects are released on an incline plane
Case-A: which is smooth.
Case-B: where friction is insufficient to provide pure rolling.
Case-C: where friction is sufficient to provide pure rolling. Force diagram for three cases are as follows: (where symbols have their usual meanings)

If the four objects given in the above question are of same mass, same radius having the same friction coefficient and are released from the same height, then at the bottom the object which will have least kinetic energy for case B will be the:View SolutionQuestion 60
In this passage a brief idea is given of the motion of the rolling bodies on an inclined plane. We will consider three cases: objects are released on an incline plane
Case-A: which is smooth.
Case-B: where friction is insufficient to provide pure rolling.
Case-C: where friction is sufficient to provide pure rolling. Force diagram for three cases are as follows: (where symbols have their usual meanings)
Two children A and B use bicycles, having wheels of ring type and disc type respectively. During a race, bicycles are given the same velocity from the bottom of the inclined bridge to ascend the bridge without pedalling, then (assuming pure rolling). View SolutionQuestion 65
A solid ball of mass m and radius r spinning with angular velocity ω falls on a horizontal slab of mass M with rough upper surface (coefficient of friction μ) and smooth lower surface. Immediately after collision the normal component of velocity of the ball remains half of its value just before collision and it stops spinning. Find the velocity of the sphere in horizontal direction immediately after the impact (given: Rω=5).
 View Solution
View SolutionQuestion 69
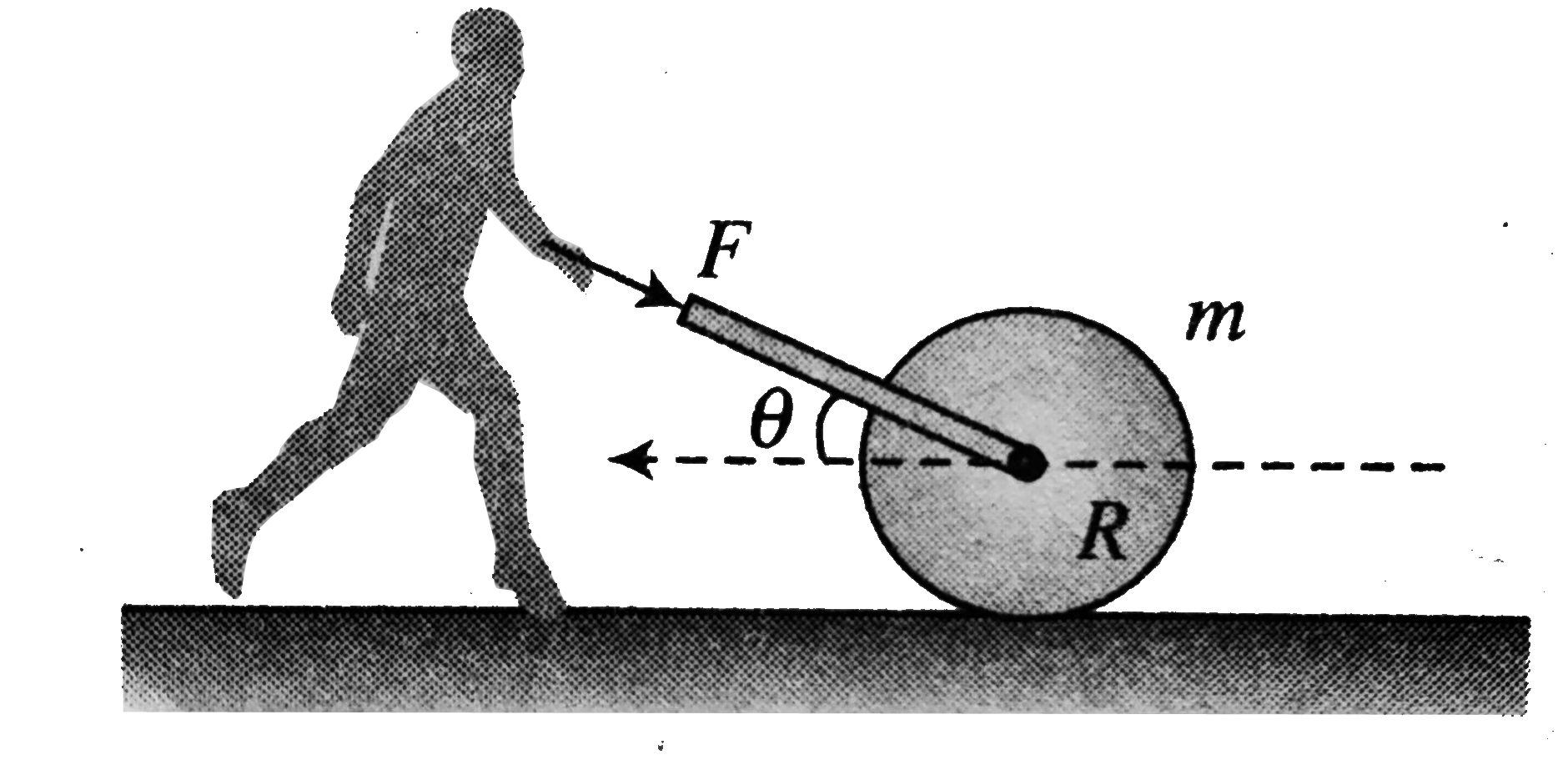
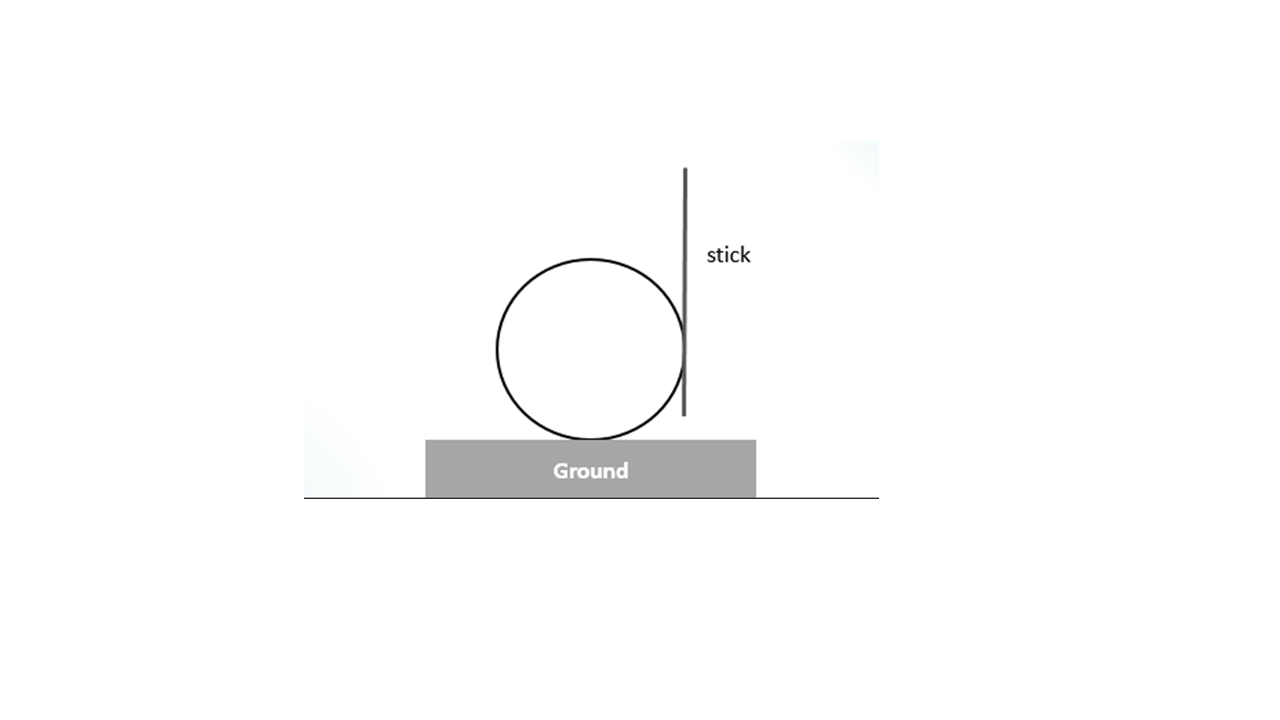
A boy is pushing a ring of mass 2 kg and radius 0.5 m with a stick as shown in the figure. The stick applies a force of 2 N on the ring and rolls it without slipping with an acceleration of 0.3m/s2. The coeffecient of friction between the ground and the ring is large enough that rolling always occur and the coefficient of friction between the stick and the ring
 View Solution
View SolutionQuestion 70
A parabolic wire as shown in the figure is located in x-y plane and carries a current l=10 amp. A unifrom magnetic field of intensity 2√2T, making an angle of 45∘ with x-axis exists throughout the plane. If the coordinates of end point 'P' of wire are (2m,1.5m) then the total force acting on the wire is:
 View Solution
View Solution