Exercise 5.2 from CENGAGE PHYSICS (ENGLISH) Chapter 25 TRAVELLING WAVES for Class 11

Class 11	PHYSICS
Chapter	TRAVELLING WAVES
CENGAGE PHYSICS (ENGLISH)	Exercise 5.2
Medium	English
Academic Year	2023-2024

Question 1
A transverse wave is travelling along a string in the positive x-axis. The

shows the photograph of the wave at an instant. Find
(a) the points moving upwards
(b) the points moving downwards
(c ) the points which have zero velocity
(d) the points which have maximum velocity View Solution
Question 2
Does the wave function $y = A_{0} {cos}^{2} (2 π f_{0} t - 2 π x / λ_{0}$ represent a wave? If yes, the determine its amplitude frequency, and wavelength. View Solution
Question 3
Does the equation
$y = + \sqrt{16 - {(2 x - t)}^{2}}$ ,
(2x-t)lt4 or (2x-t)gt-4,
=0,otherwise
represent a wave? If yes, then find the amlityde and the phase velocity.View Solution
Question 4
The equation of a travelling wave is given by
$y = + \frac{b}{a} \sqrt{a^{2} - {(x - c t)}^{2}} w h e r e - a < x < a$
=0,otherwise
Find the amplitude and the wave velocity for the wave. what is the initial particle velocity at the position $x = a / 2$ ? View Solution
Question 5
Does a travelling wave in one dimension represented by a function of a linear combination of x and t,i.e., $y = f (a x \pm b t)$ represented a travelling wave?View Solution
Question 6
A wave is propagating on a long stretched string along its length taken as the positive x-axis. The wave equation is given as
$y = y_{0} e^{- {(\frac{t}{T} - \frac{x}{λ})}^{2}}$
where $y_{0} = 4 m m, T = 1.0 s and λ = 4 c m$ .(a) find the velocity of wave. (b) find the function $f (t)$ giving the displacement of particle at x=0. (c) find the function g(x) giving the shape of the string at t=0.(d) plot the shape g(x) of the string at t=0 (e) Plot of the shape of the string at t=5s.View Solution
Question 7
Equation of a transverse wave travelling in a rope is given by
$y = 5 sin (4.0 t - 0.02 x)$
where y and x are expressed in cm and time in seconds. Calculate
(a) the amplitude, frequency,velocity and wavelength of the wave.
(b) the maximum transverse speed and acceleration of a particle in the rope.View Solution
Question 8
The length of the wire shown in figure between the pulley is 1.5 m and its mass is 12.0 g. Find the frequency of vibration with which the wire vibrates in two loops leaving the middle point of the wire between the pulleys at rest.
View Solution
Question 9
The equation of a travelling sound wave is $y = 6.0 sin (600 t - 1.8 x)$ where y is measured in $10^{- 5} m$ , t in second and x in metre. (a) Find the ratio of the displacement amplitude of the particles to the wavelength of the wave. (b) Find the ratio of the velocity amplitude of the particles to the wave speed. View Solution
Question 10
The equation of a travelling sound wave is $y = 6.0 sin (600 t - 1.8 x)$ where y is measured in $10^{- 5} m$ , t in second and x in metre. (a) Find the ratio of the displacement amplitude of the particles to the wavelength of the wave. (b) Find the ratio of the velocity amplitude of the particles to the wave speed. View Solution
Question 11
Spherical waves are emitted from a $1.0 W$ source in an isotropic non-absorbing medium. What is the wave intesity $1.0 m$ from the source? View Solution
Question 12
A wave travels out in all direction from a point source. Justify the expression $y = (\frac{a_{0}}{r}) sin k (r - v t)$ , at a distance r from the source. Find the speed, periodicity and intensity of the wave.what are the dimensions of $a_{0}$ ?View Solution
Question 13
For plane waves in the air of frequency 1000 Hz and the displace amplitude $2 \times 10^{- 8} m$ , deduc (i) the velocity amplitude, and (ii) the intensity. (Take p= 1.3 kg//m^(3),c=340 m//s) View Solution
Question 14
A heavy uniform rope is held vertically and is tensioned by clamping it to a rigid support at the lower end. A wave of a certain frequency is set up at the lower end. Will the wave travel up the rope with the same speed? View Solution
Question 15
What is the phase diffrence between the particle 1 and 2 located as shown in View Solution
Question 16
Show that $(a) y = {(x + v t)}^{2}, (b) y = {(x + t)}^{2}, (c) y = {(x - v t)}^{2}$ , and (d) y=2 sin xcos vt are each a solution of one dimensional wave equation but not (e) y=x^(2)-v^(2)t^(2) $and (f)$ y=sin 2x cos vt.View Solution
Question 17
For a travelling harmonic wave $y = 2.0 cos (10 t - 0.0080 x + 0.35)$ , where x and y are in centimetres and t in seconds. What is the phase difference between oscillatory motion of two points separated by a distance of (a) 4cm (b) 0.5 cm (c ) $λ / 2$ (d) $3 λ / 4$ View Solution
Question 18
The

shows two snapshots, each of a wave travelling along a particular string. The phase for the waves are given by (a) 4x-8t (b) 8x-16t. Which phase corresponds to which waves in View Solution
Question 19
A circular loop of string rotates about its axis on a frictionless horizontal plane at a uniform rate so that the tangential speed of any particle of the string is v. if a small transvers disturbance is produced at a point of the loop,with what speed (relative to the string) will this disturbance travel on the string? View Solution
Question 20
A sinusoidal wave is propagating along a streched string that lies along the x-axis. The displacement of the string as a function of time is graphed in for particles at x-0 and at x=0.0900 m. (a) what is the amplitude of the wave? (b)what is the period of the wave? (c ) you are told that the two points x=0 and x=0.0900 m are within one wavelength of each other. if the wave is moving in the +x-direction, determine the wavelength and the wave speed. (d) if instead the wave is moving in the -x-direction, determine the wavelength and the wave speed. (e) would it be possible to derermine definitely the wavelength in parts (c ) and (d) if you were not told that the two points were within one wavelength of each other? why ot why not?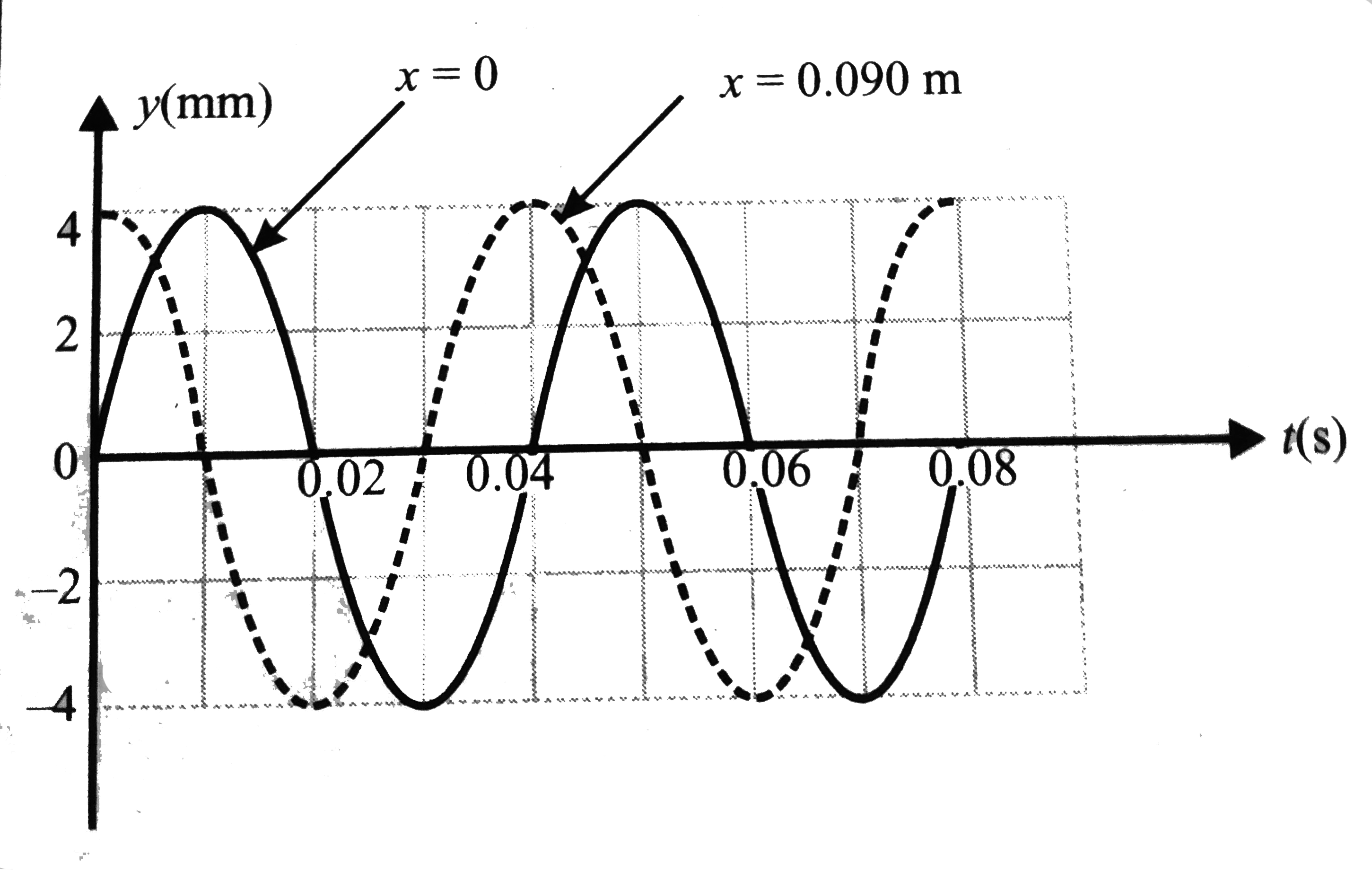 View Solution
Question 21
A simple harmonic oscillator at the point x=0 genrates a wave on a rope. The oscillator operates at a frequency of 40.0 Hz and with an amplitude of 3.00 cm. the rope has a linear mass density of $50.0 g / m$ and is strectches with a tension of 5.00 N. (a) determine the speed of the wave. (b) find the wavelength. (c ) write the wave function y(x,t) for the wave, Assume that the oscillator has its maximum upward displacement at time t=0. (d) find the maximum transverse acceleration at time t=0. (d) find the maximum transverse of points on the rope. (e) in the discussion of transverse waves in this chapter, the force of gravity was ignored. is that a reasonable assumption for this wave? explain. View Solution
Question 22
A piano wire with mass 3.00 g and length 80.0 cm is stretched with a tension of 25.0 N. A wave with frequancy 120.0 Hz and amplitude 1.6 mm travels along the wire. (a) calculate the average power carried by the wave. (b) what happenes to the avarage power if the wave amplitude is halved? View Solution
Question 23
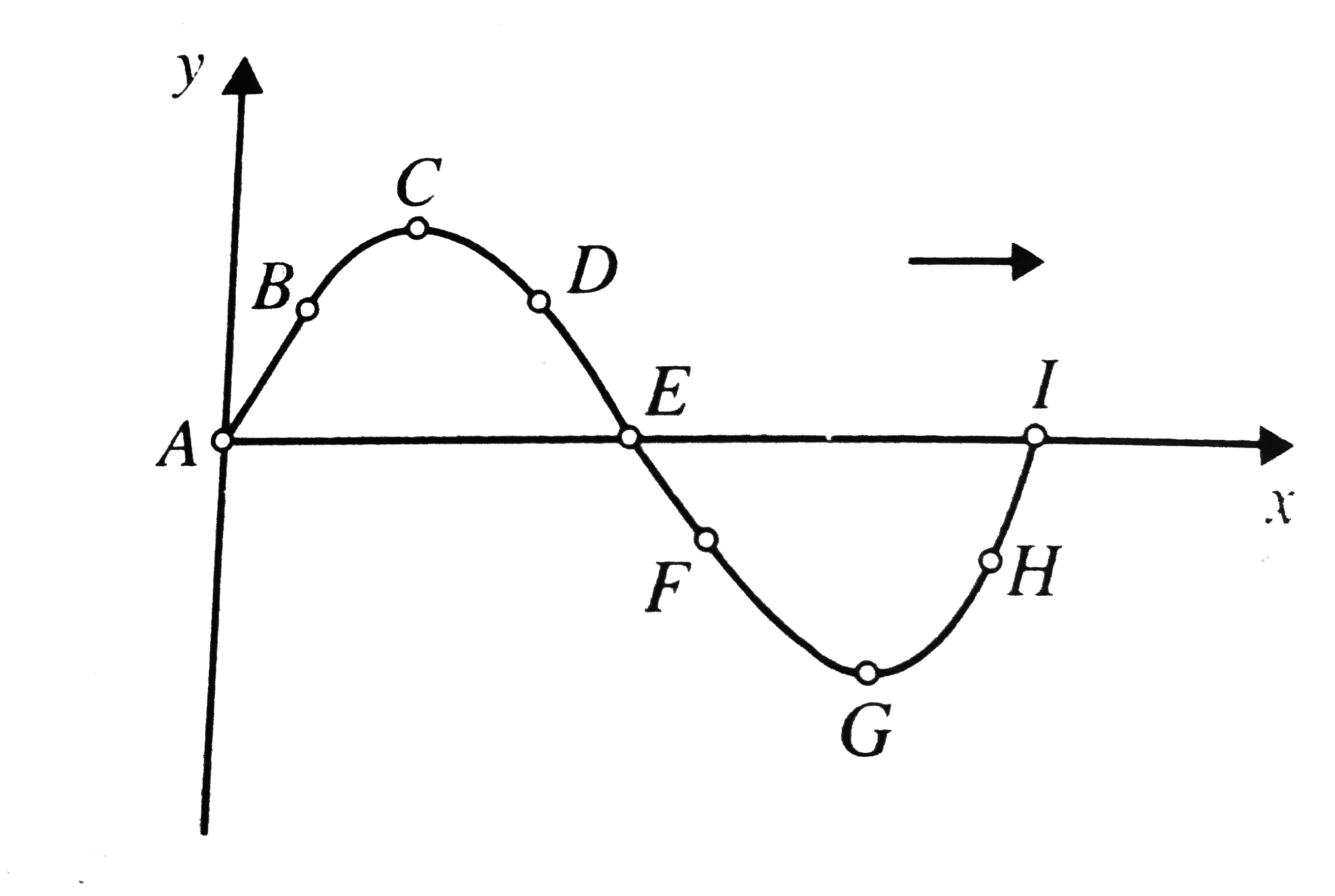
A wave on a string is described by $y (x, t) = A cos (k x - ω t)$ . (a) Graph $y, v_{y}$ , and $a_{y}$ as function of x for time t=0. (b) consider the following points on the string: (i) x=0,(ii) x=pi//4k, (iii) x=pi//2k, (iv)x=3pi//4k, (v)x=pi//k, (vi)x=5pi//4k, (vii) x=3pi//2k, (viii) x=7pi//4k. For a particle at each of these points at t=0, describes in words whether the particle is moving and in what direction, and whether the particle is speeding up, slowing down, or instantaneously not acceleraring.View Solution

All Exercises from CENGAGE PHYSICS (ENGLISH) Class 11 PHYSICS TRAVELLING WAVES

Home
Ask Doubt
Profile