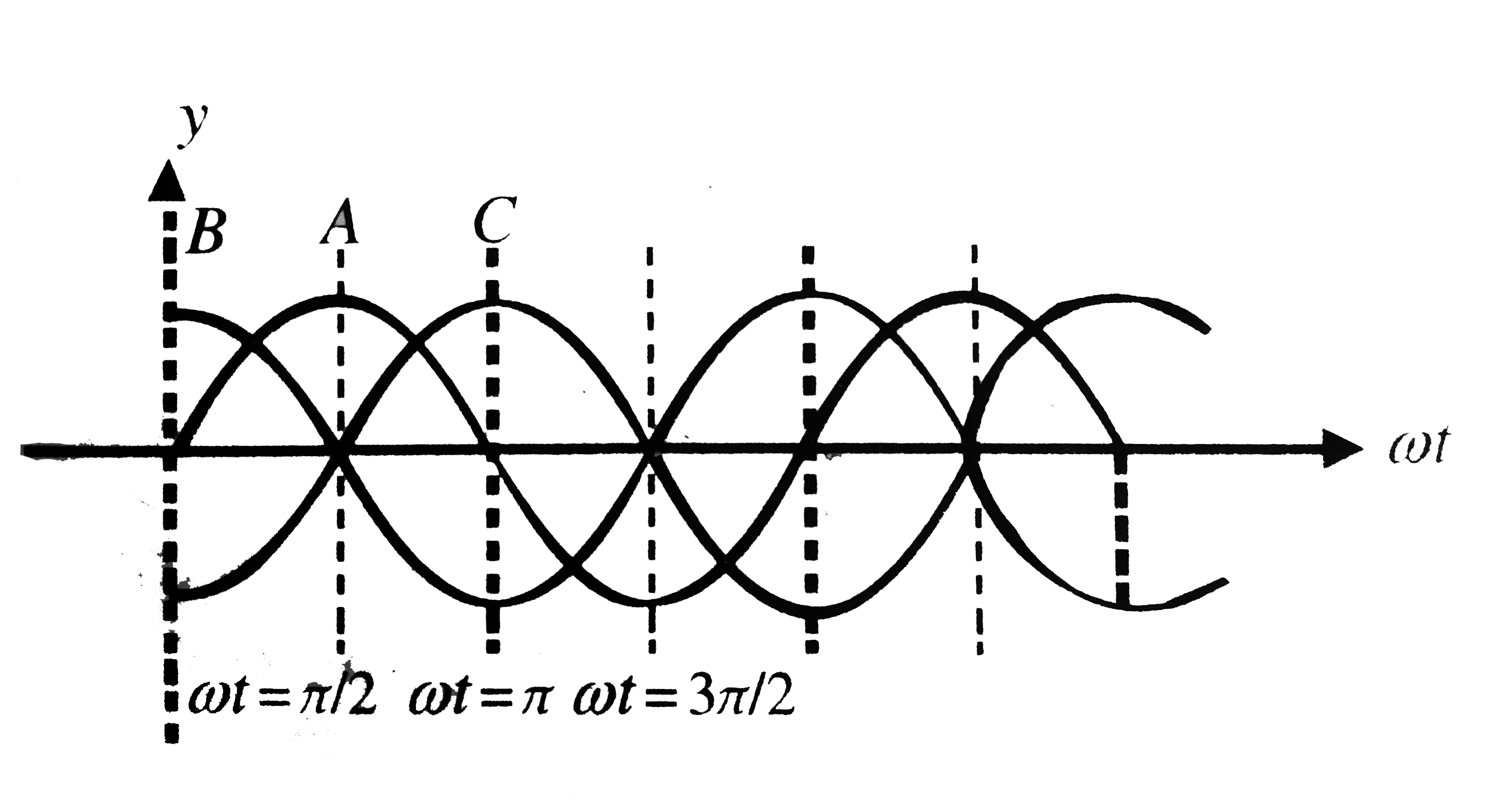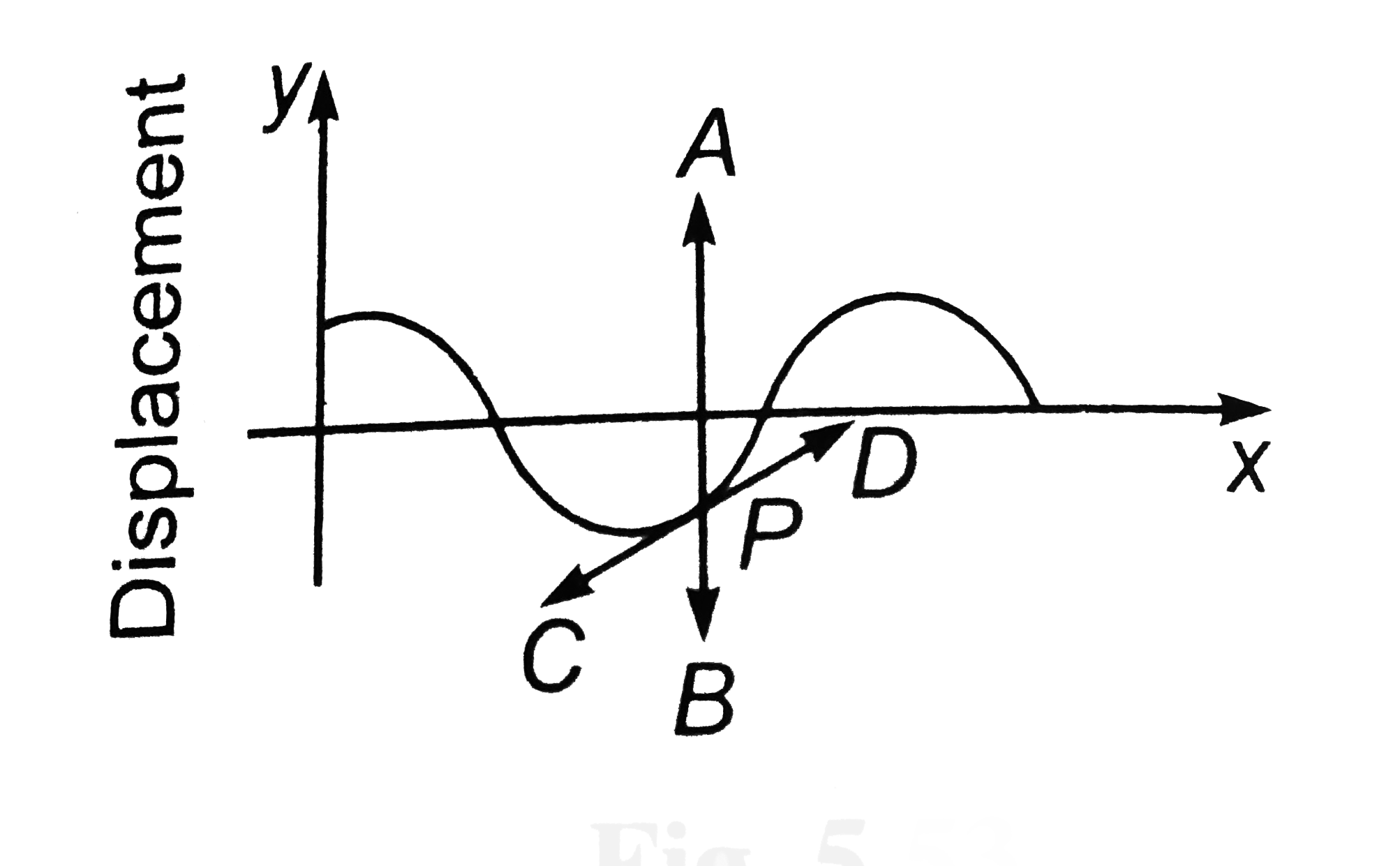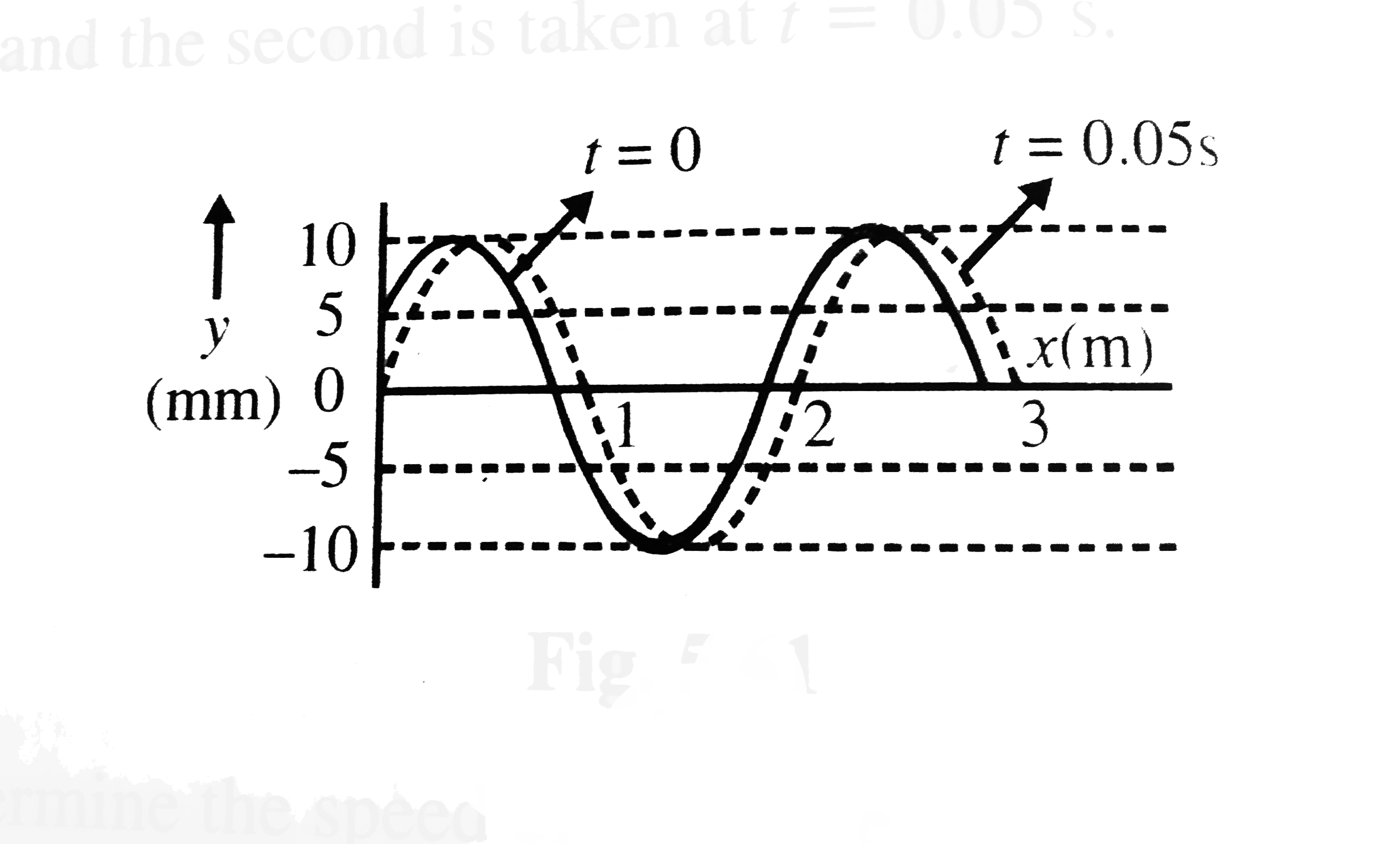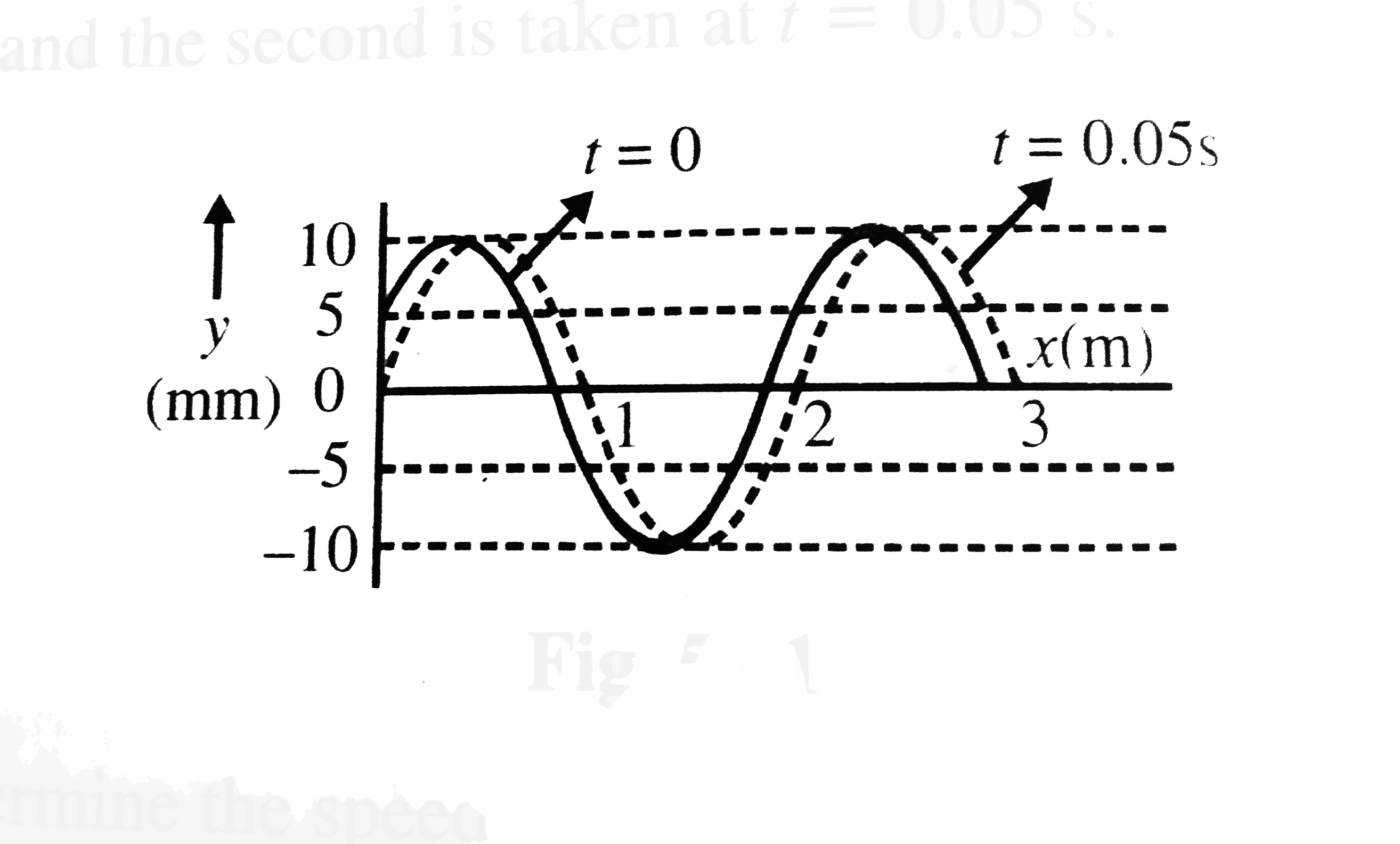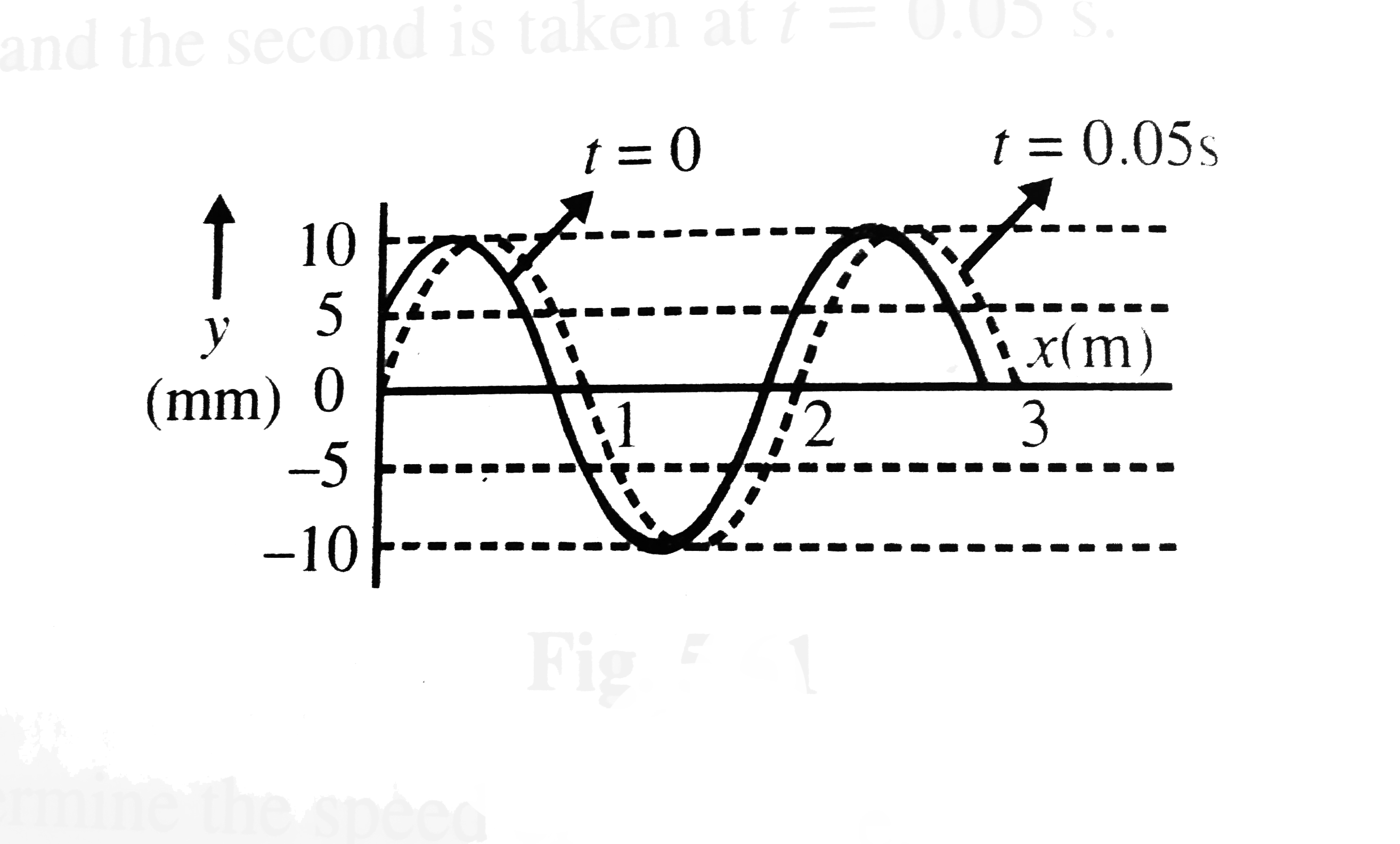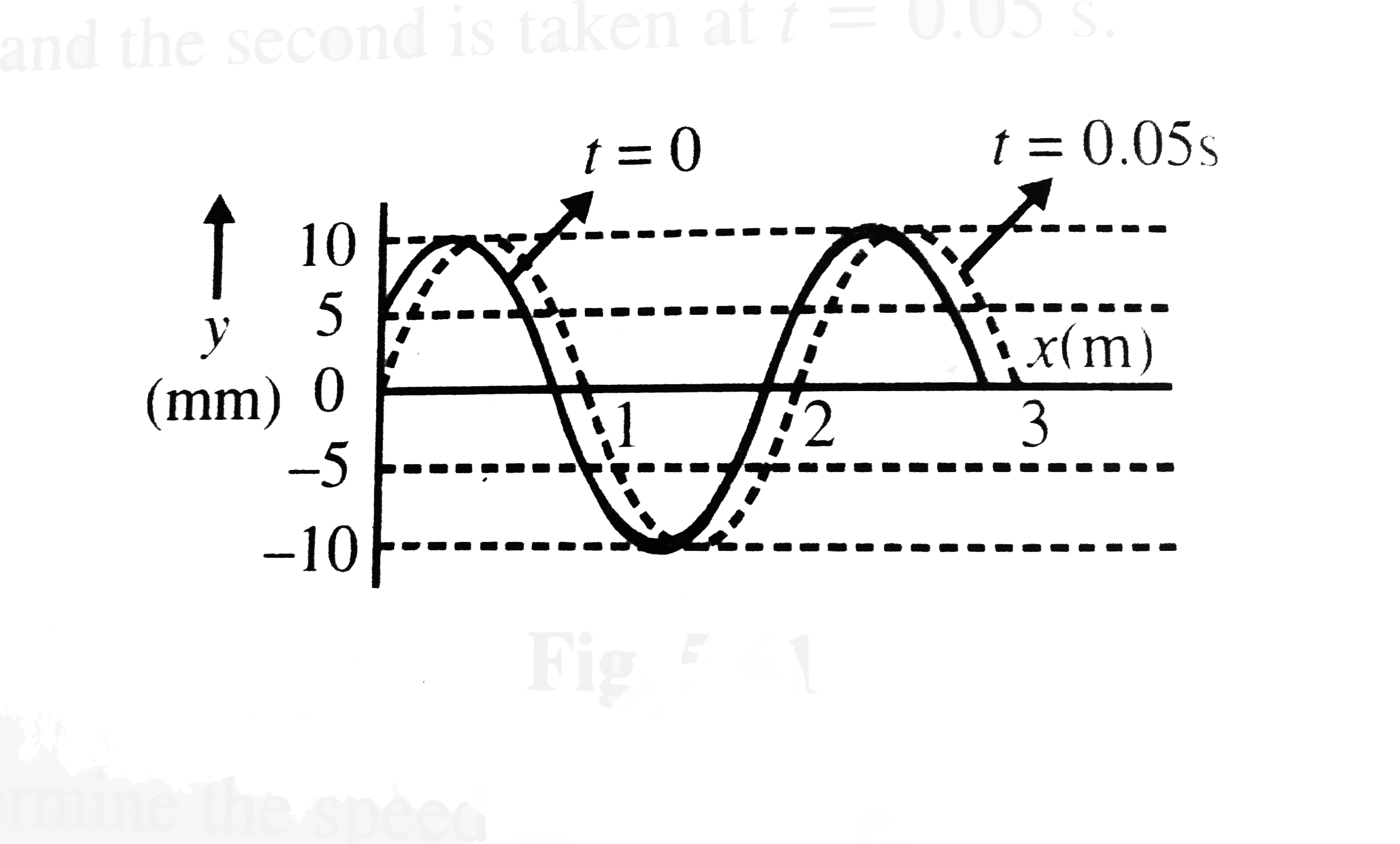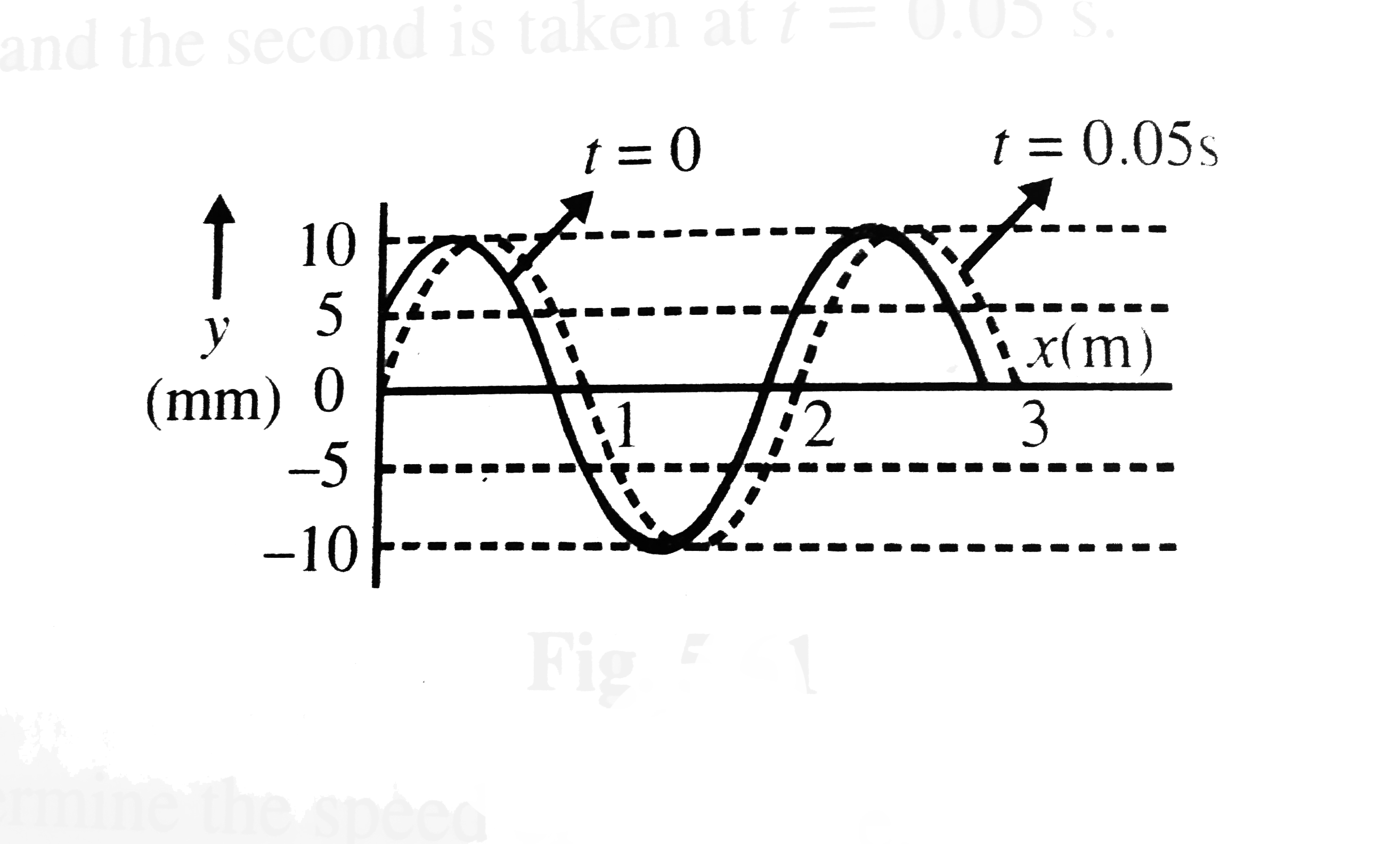Exercise 5.2 from CENGAGE PHYSICS (ENGLISH) Chapter 11:TRAVELLING WAVES for Class 11
| Class 11 | PHYSICS |
| Chapter | TRAVELLING WAVES |
| CENGAGE PHYSICS (ENGLISH) | Exercise 5.2 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 8
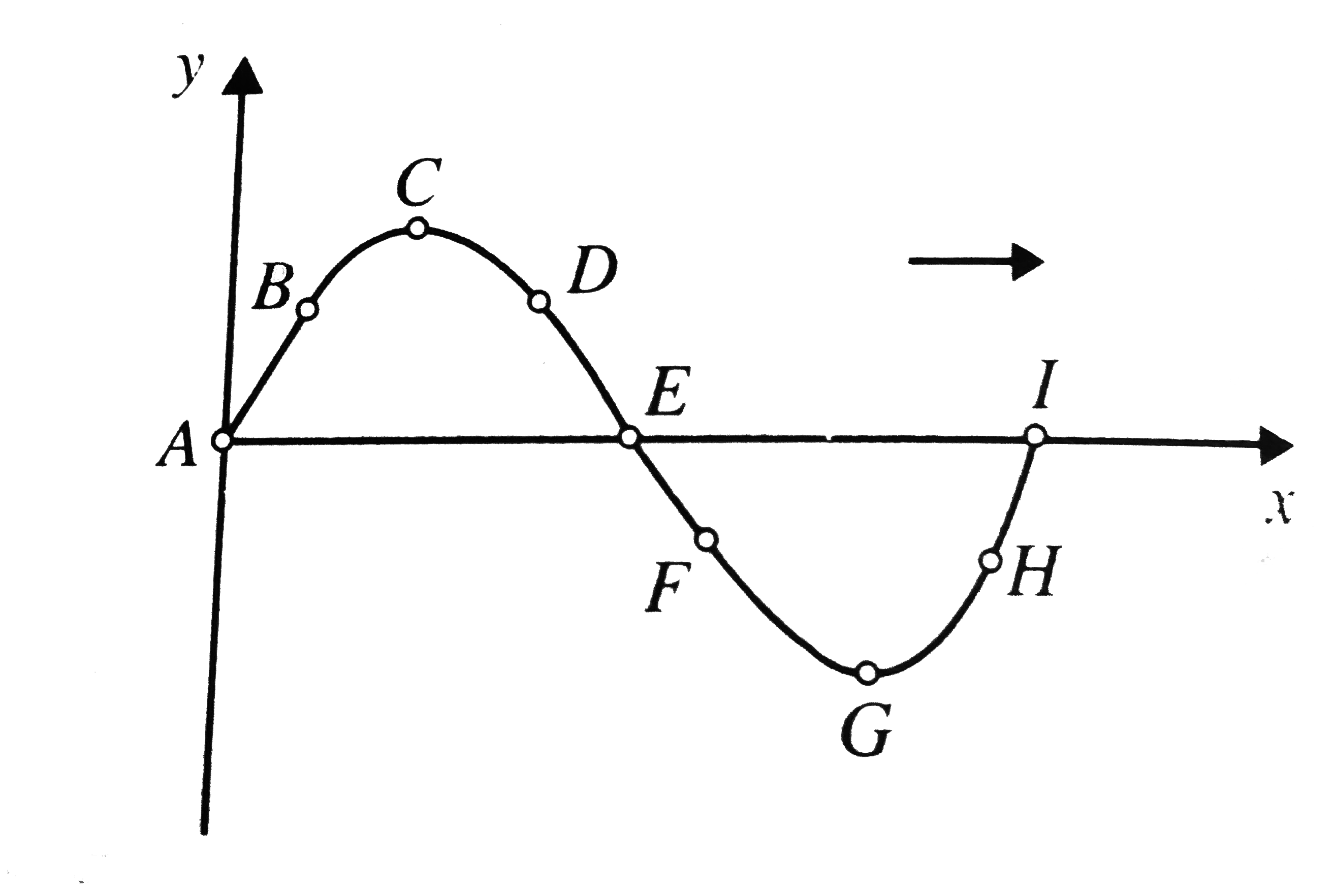
Waves are generated on a water surface. Calculate the phase difference between two points A and B, when (i) A and B lie on the same wavefront at a distance of 2λ between them
(ii) A and B lie on successive crests separated by 1 m
(iii) A and B lie on succesive through separated by 1.5 m View SolutionQuestion 15
A wave is propagating on a long stretched string along its length taken as the positive x-axis. The wave equation is given as
y=y0e−(tT−xλ)2
where y0=4mm,T=1.0sandλ=4cm.(a) find the velocity of wave. (b) find the function f(t) giving the displacement of particle at x=0. (c) find the function g(x) giving the shape of the string at t=0.(d) plot the shape g(x) of the string at t=0 (e) Plot of the shape of the string at t=5s.View SolutionQuestion 16
Equation of a transverse wave travelling in a rope is given by
y=5sin(4.0t−0.02x)
where y and x are expressed in cm and time in seconds. Calculate
(a) the amplitude, frequency,velocity and wavelength of the wave.
(b) the maximum transverse speed and acceleration of a particle in the rope.View SolutionQuestion 18
The equation of a travelling sound wave is y=6.0sin(600t−1.8x) where y is measured in 10−5m, t in second and x in metre. (a) Find the ratio of the displacement amplitude of the particles to the wavelength of the wave. (b) Find the ratio of the velocity amplitude of the particles to the wave speed. View SolutionQuestion 19
The equation of a travelling sound wave is y=6.0sin(600t−1.8x) where y is measured in 10−5m, t in second and x in metre. (a) Find the ratio of the displacement amplitude of the particles to the wavelength of the wave. (b) Find the ratio of the velocity amplitude of the particles to the wave speed. View SolutionQuestion 28
A circular loop of string rotates about its axis on a frictionless horizontal plane at a uniform rate so that the tangential speed of any particle of the string is v. if a small transvers disturbance is produced at a point of the loop,with what speed (relative to the string) will this disturbance travel on the string? View SolutionQuestion 29
A sinusoidal wave is propagating along a streched string that lies along the x-axis. The displacement of the string as a function of time is graphed in for particles at x-0 and at x=0.0900 m. (a) what is the amplitude of the wave? (b)what is the period of the wave? (c ) you are told that the two points x=0 and x=0.0900 m are within one wavelength of each other. if the wave is moving in the +x-direction, determine the wavelength and the wave speed. (d) if instead the wave is moving in the -x-direction, determine the wavelength and the wave speed. (e) would it be possible to derermine definitely the wavelength in parts (c ) and (d) if you were not told that the two points were within one wavelength of each other? why ot why not?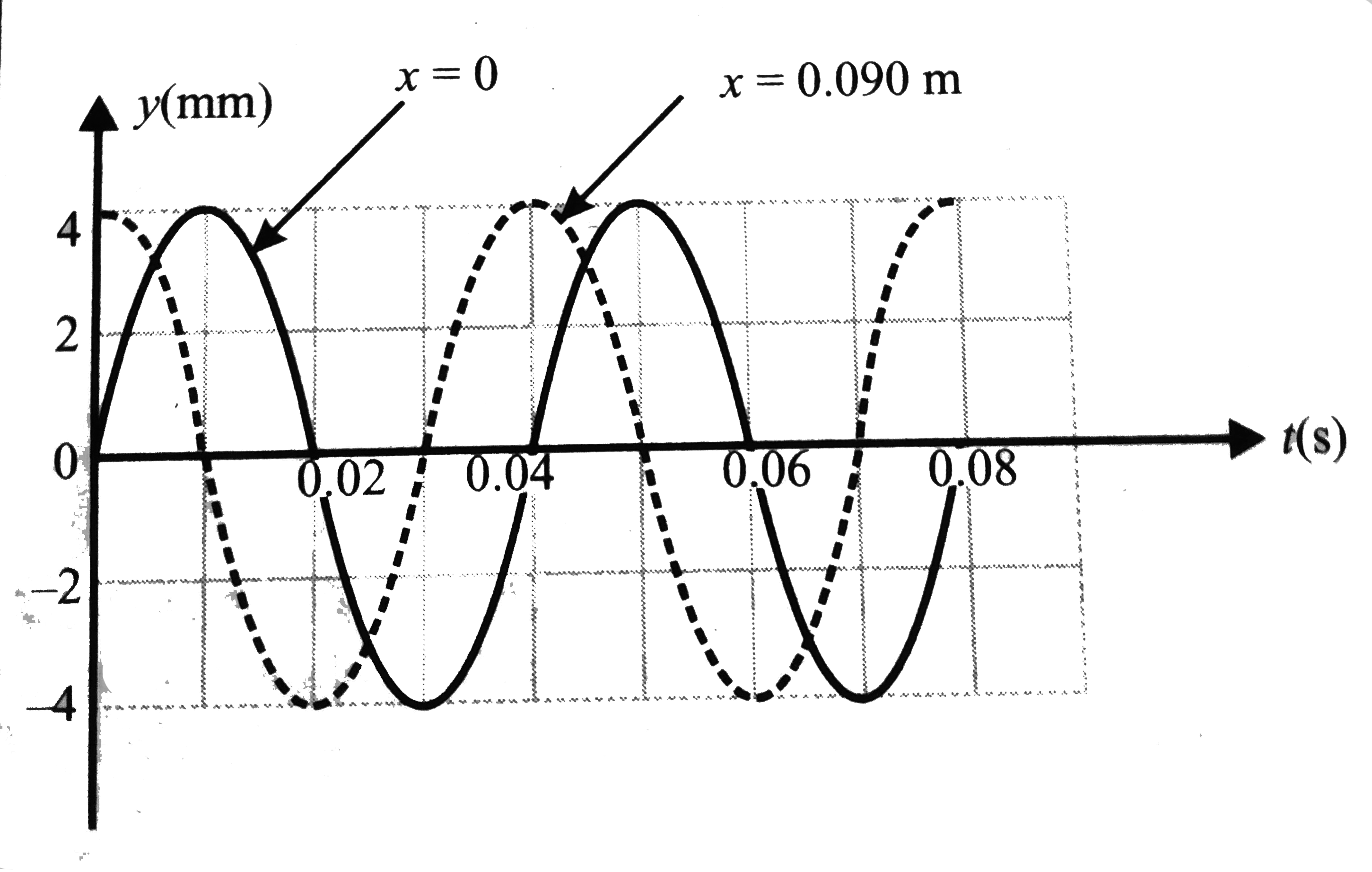
View SolutionQuestion 30
A simple harmonic oscillator at the point x=0 genrates a wave on a rope. The oscillator operates at a frequency of 40.0 Hz and with an amplitude of 3.00 cm. the rope has a linear mass density of 50.0g/m and is strectches with a tension of 5.00 N. (a) determine the speed of the wave. (b) find the wavelength. (c ) write the wave function y(x,t) for the wave, Assume that the oscillator has its maximum upward displacement at time t=0. (d) find the maximum transverse acceleration at time t=0. (d) find the maximum transverse of points on the rope. (e) in the discussion of transverse waves in this chapter, the force of gravity was ignored. is that a reasonable assumption for this wave? explain. View SolutionQuestion 31
A piano wire with mass 3.00 g and length 80.0 cm is stretched with a tension of 25.0 N. A wave with frequancy 120.0 Hz and amplitude 1.6 mm travels along the wire. (a) calculate the average power carried by the wave. (b) what happenes to the avarage power if the wave amplitude is halved? View SolutionQuestion 32
A wave on a string is described by y(x,t)=Acos(kx−ωt). (a) Graph y,vy, and ay as function of x for time t=0. (b) consider the following points on the string: (i) x=0,(ii) x=pi//4k, (iii) x=pi//2k, (iv)x=3pi//4k, (v)x=pi//k, (vi)x=5pi//4k, (vii) x=3pi//2k, (viii) x=7pi//4k. For a particle at each of these points at t=0, describes in words whether the particle is moving and in what direction, and whether the particle is speeding up, slowing down, or instantaneously not acceleraring.View SolutionQuestion 33
A 100Hz sinusoidal wave is travelling in the posotive x-direction along a string with a linear mass density of 3.5×10−3kg/m and a tension of 35N. At time t=0, the point x=0 , has maximum displacement in the positive y-direction. Next when this point has zero displacement, the slope of the string is π/20. Which of the following expression represent (s) the displacement of string as a function of x(in metre) and t (in second) View SolutionQuestion 34
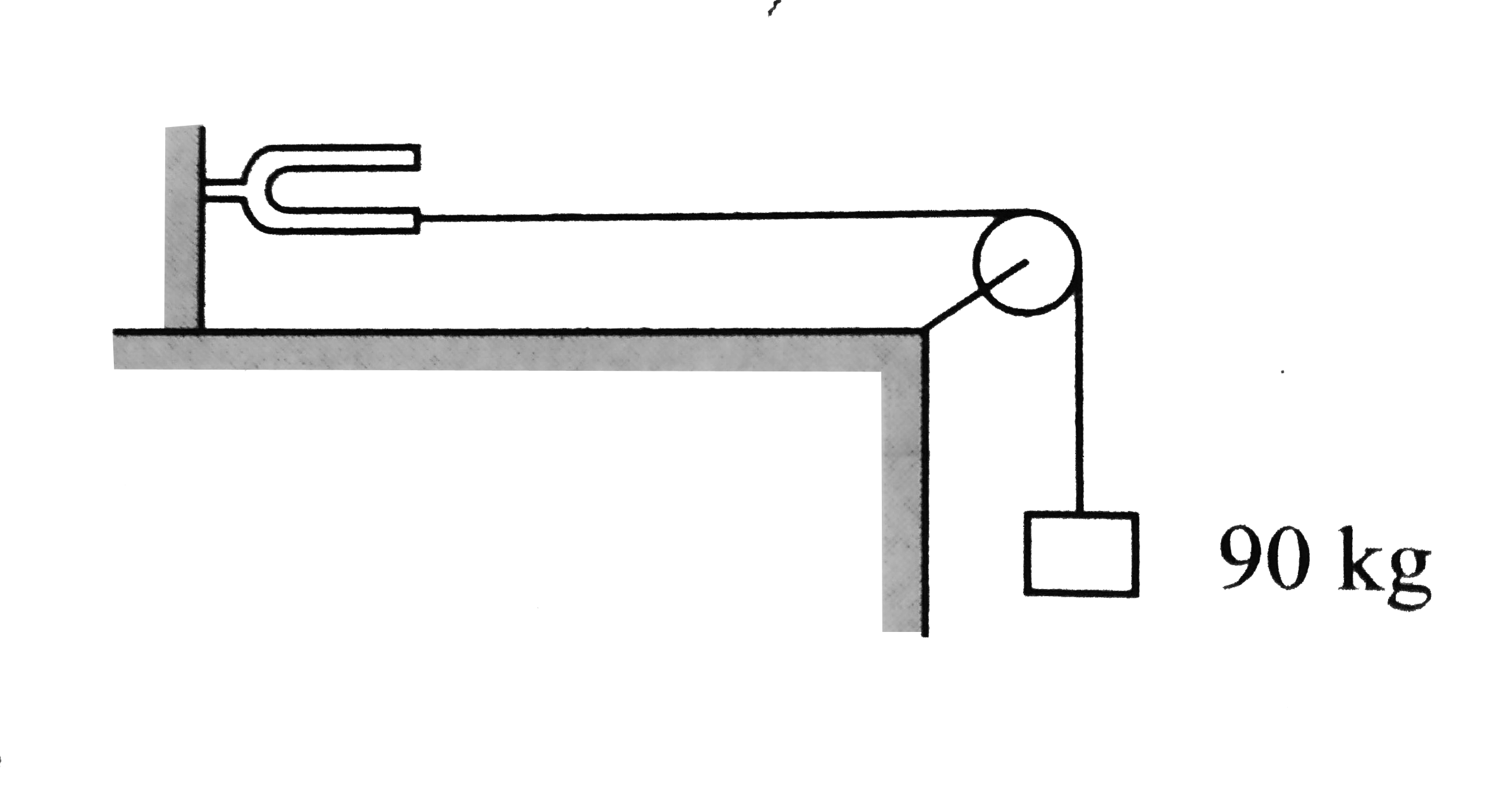
One end of a long string of linear mass density 10−2kgm−1 is connected to an electrically driven tuning fork of frequency 150 Hz. The other end passes over a pulley and is tied to a pan containig a mass of 90 kg. the pulley end absorbs all the incoming energy so that reflected waves from this end have neglidible amplitude , At t =0, the left end (fork end ) of the string is at x=0 has a transverse displacement of 2.5 cm and is moving along positive y-direction. the amplitude of the wave is 5 cm. write down the transverse displacement y (in cetimetres) as function of x(in metres) and t (in seconds ) that describes the wave on the string.
View SolutionQuestion 35
An harmonic wave has been set up on a very long string which travels along the length of the string. The wave has a frequency of 50 Hz, amplitude 1 cm and wavelength 0.5 m. find
(a) the time taken by the wave to travel a distance of 8 m along the length of string (b) the time taken by a point on the string to travel a distance of 8 m, once the wave has reached the point and sets it into motion (c ) also. consider the above case when the amplitude gets doubled View SolutionQuestion 38
A steel wire has a mass of 50g/m and is under tension 450N.
(a) Find the maximum average power that can be carried by the transverse wave in the wire if the amplitude not to exceed 20% of the wavelength. (b) The change in maximum average power if the mass per unit length of the wire is doubled. (Useπ2≅10.)View SolutionQuestion 39
A wave is propagating on a long stretched string along its length taken as the positive x-axis. The wave equation is given as
y=y0e−(tT−xλ)2
where y0=4mm,T=1.0sandλ=4cm.(a) find the velocity of wave. (b) find the function f(t) giving the displacement of particle at x=0. (c) find the function g(x) giving the shape of the string at t=0.(d) plot the shape g(x) of the string at t=0 (e) Plot of the shape of the string at t=5s.View SolutionQuestion 41
A 4.0 kg block is suspended from the ceiling of an elevator through a string having a linear mass desity of 19.2×10−3kgm−1. Find the speed (with respect to the string) with which a wave pulse can proceed on the string if the elavator accelerates up at the rate of 2.0ms−2.Takeg=10ms−2.View SolutionQuestion 43
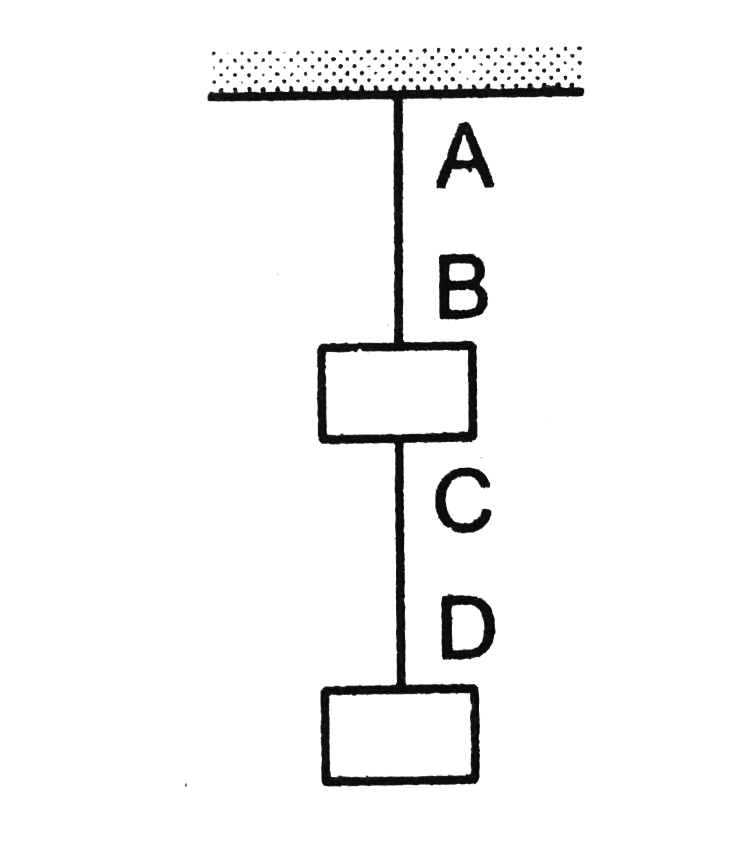
Two blocks each having a mass of 3.2 kg are connected by a wire CD and the system is suspended from the ceiling by another wire AB . The linear mass density of the wire AB is 10 g /m and that of CD is 8gm−1. Find the speed of a transverse wave pulse produced in AB and in CD.
View SolutionQuestion 44
A transverse harmonic wave of amplitude 0.01 m is genrated at one end (x=0) of a long horizontal string by a tuning fork of frequency 500 Hz. At a given instant of time the displacement of the particle at x=0.1 m is -0.005 m and that of the particle at x=0.2 m is +0.005 m. calculate the wavelength and the wave velocity. obtain the equetion of the wave assuming that the wave is traveling along the + x-direction and that the end x=0 is at he equilibrium position at t=0. View SolutionQuestion 45
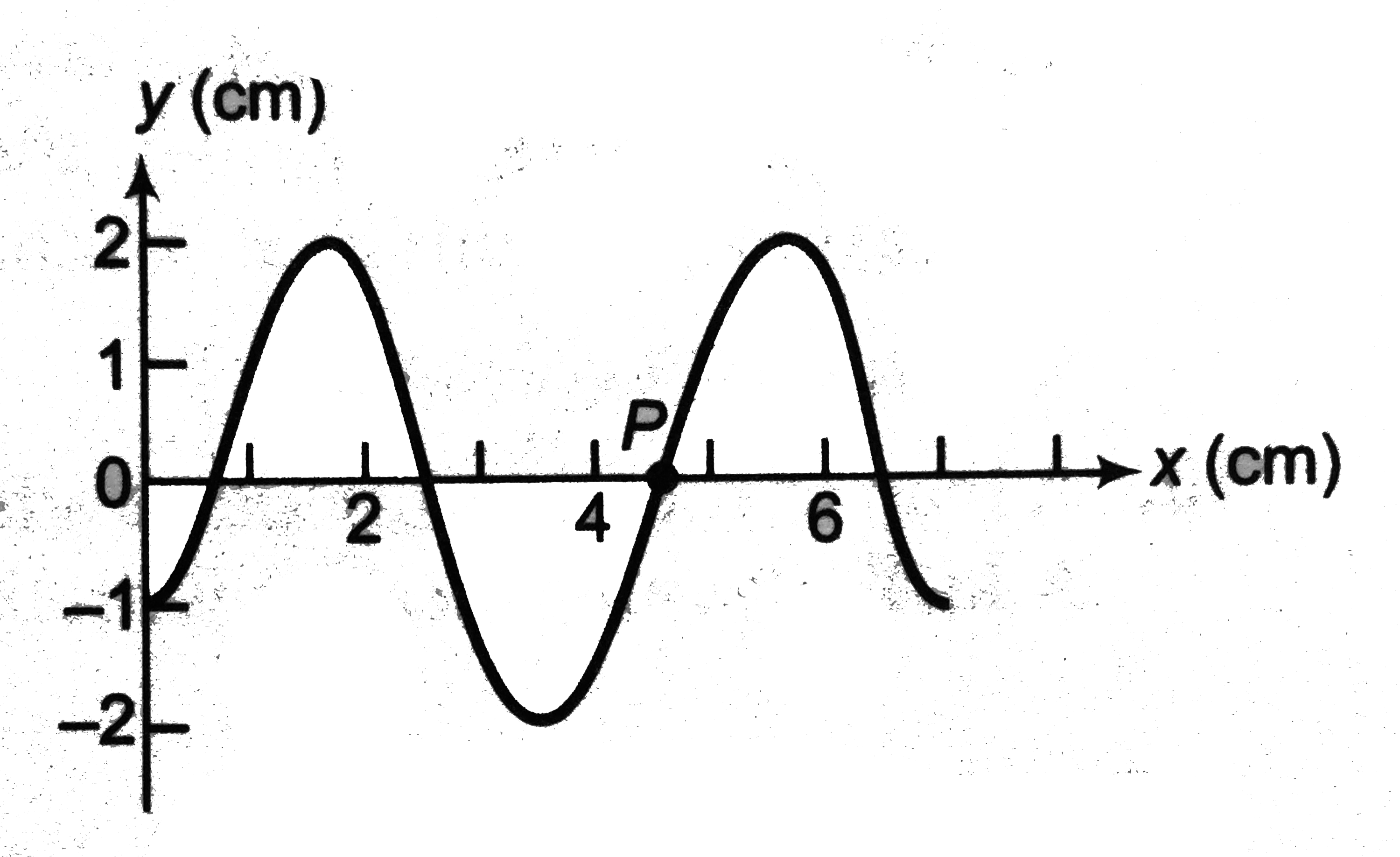
The given figure shows the position of a medium particle at t=0, supporting a simple harmonic wave travelling either along or opposite to the positive x-axis.
(a) write down the equation of the curve.
(b) find the angle θ made by the tangent at point P with the x-axis.
(c ) If the particle at P has a velocity vpm/s, in the negative y-direction, as shown in figure, then determine the speed and direction of the wave.
(d) find the frequency of the wave.
(e) find the displacement equation of the particle at the origin as a function of time.
(f) find the displacement equation of the wave.View SolutionQuestion 47
The equation of a progressive wave travelling along a string is given by
y=10sinπ(0.01x−2.00t)
where x and y are in centimetres and t in seconds. Find the (a) velocity of a particle at x=2 m and t=5/6 s. (b) acceleration of a particle at x=1 m and t=1/4 s. also find the velocity amplitude and acceleration amplitude for the wave. View SolutionQuestion 65
Two blocks of masses 40 kg and 20 kg are connected by a wire that has a linear mass density of 1g/m. These blocks are being pulled across horizontal frictionless floor by horizontal force F that is applied to 20 kg block. A transverse wave travels on the wave between the blocks with a speed of 400m/s (relative to the wire). the lmass of the wire is negligible compared to the mass of the blocks. the magnitude of F is View SolutionQuestion 73
Sinusoidal waves 5.00cm in amplitude are to be transmitted along a string having a linear mass density equal to 4.00×10−2kg/m. If the source can deliver a maximum power of 90W and the string is under a tension of 100N, then the highest frequency at which the source can operate is (take π2=10)View SolutionQuestion 76
A transverse sinusoidal wave is generated at one end of a long horizontal string by a bar that moves the end up and down through a distance by 2.0cm. the motion of bar is continuous and is repeated regularly 125 times per second. If klthe distance between adjacent wave crests is observed to be 15.6cm and the wave is moving along positive x−direction, and at t=0 the element of the string at x=0 is at mean position y=0 and is moving downward, the equation of the wave is best described by View SolutionQuestion 78
A sinusoidal wave is genrated by moving the end of a string up and down, periodically. The genrated must apply the energy has ………..x and least power when the end of the string attached to genrated to genrated has ………..Y. the most suitable option which correctly fills blanks X and Y, is View SolutionQuestion 80
Two canoes are 10m apart on a lake . Each bobs up and down with a period of 4.0s. When one canoe is at its highest point , the other canoe is at its lowest point . Both canoes are always within a single cycle of the waves . The canoes are always within a single cycle of the waves . The speed of wave is .View SolutionQuestion 82
A transverse wave on a string travelling along + ve x-axis has been shown in the figure below:
The mathmetical form of the shown wave is
y=(3.0cm)sin[2π×0.1t−2π100x]
where t is in seconds and x is in centimetres. Find the total distance travelled by the particle at (1) in 10 min 15 s. measured from the instant shown in the figure and direction of its motion at the end of this time.
View SolutionQuestion 83
A water surface is moving at a speed of 15m/s. When he is surfing in the direction of wave, he swing upwards every 0.8 s because of wave crests. While surfing in opposite direction to that of wave motion, he swings upwards every 0.6 s. determine the wavelength of transverse component of the water wave. View SolutionQuestion 84
A transverse wave on a string has an amplitude of 0.2 m and a frequency of 175 Hz. Consider a particle of the string at x=0. it begins with a displacement y=0, at t=0, according to equation y=0.2sin(kx±ωt). How much time passed between the first two instant when this particle has a displacement of y=0.1 m?View SolutionQuestion 87
A harmonic wave has been set up on a very long string which travels along the length of string. The wave has frequency of 50 Hz. Amplitude 1 cm and wavelength 0.5 m. for the above described wave.
Statement (i): time taken by a point on the string to travel a distance of 8 m along the length of string is 0.32 s.
Statement (ii): time taken by a point in the string to travel a distance of 8m, once the wave has reached at that point and sets it into motion is 0.32 s. View SolutionQuestion 89
A wave is represented by the equation
y=Asin(10πx+15πt+π/3)
Where x is in metre and t is in second.
a wave travelling in the positive x-direction with a velocity of 1.5 m/s
a wave travelling in the negative x-direction with a velocity 1.5 m/s
a wave travelling in the negative x-direction with a wavelength of 0.2 m
a wave travelling in the positive x-direction with a wavelength 0.2 m View SolutionQuestion 91
A transverse waves is travelling in a string. Study following statement.
(i) Equation of the wave is equal to the shape of the string at an instant t. (ii) Equation of thhe wave is general equation for displacement of a particle of the string (iii) Equation of the wave must be sinusoidal equation (iv) Equation of the wave is an equation for displacement of the particle at one end only.correct statement are View SolutionQuestion 99
A string of length 2L, obeying hooke's law, is stretched so that its extension is L. the speed of the transverse wave travelling on the string is v. If the string is further stretched so that the extension in the string becomes 4L. The speed of transverse wave travelling on the string will beView SolutionQuestion 111
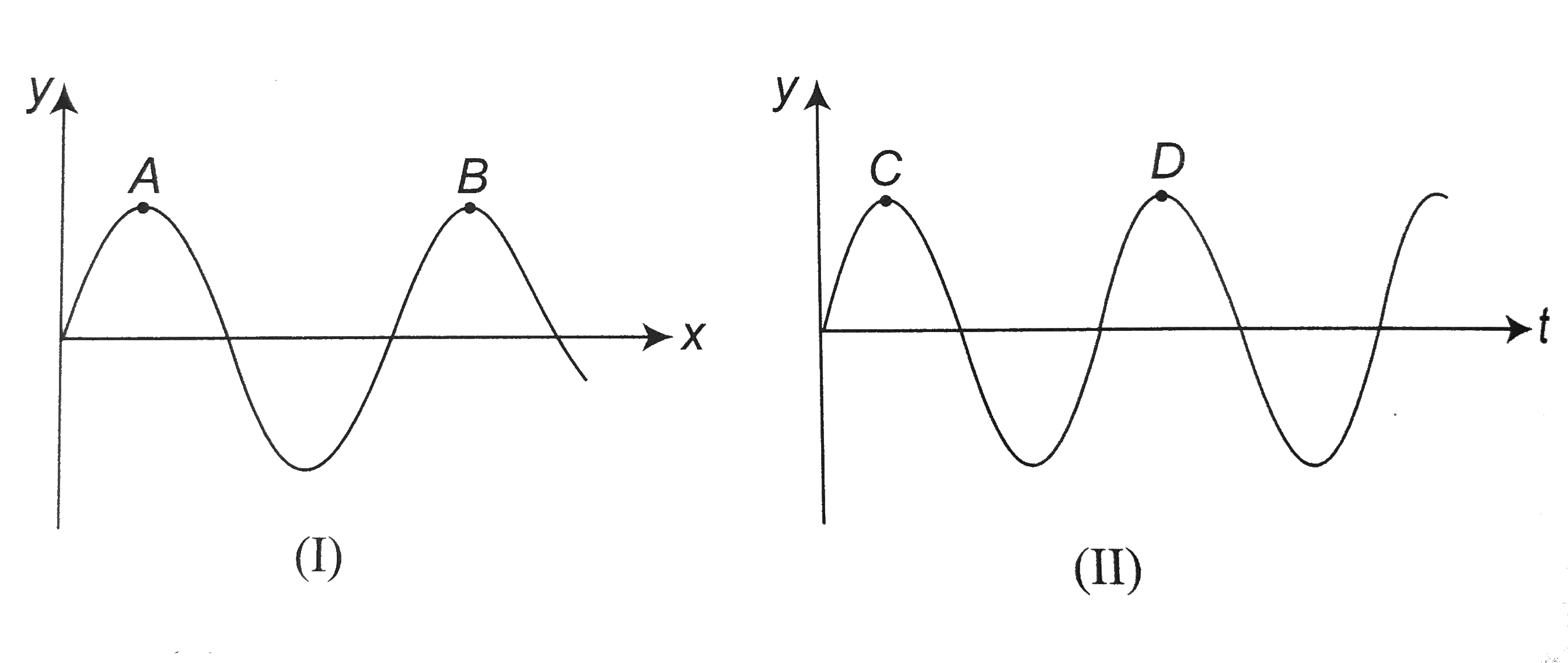
The same progressive wave is represented by two graphs I and II. Graph I shows how the displacement y varies with the distance x along the wave at a given time. Graph II shows how y varies with time t at a given point on the wave. The ratio of measurements AB to CD, marked on the curves represents:View SolutionQuestion 114
A simple harmonic progressive wave in a gas has a particle displacement of y=a at time t=T/4 at the orgin of the wave and a particle velocity of y =v at the same instant but at a distance x=λ/4 from the orgin where T and λ are the periodic time and wavelength of the wave respectively. then for this wave.View SolutionQuestion 133
A wire of 9.8×10−3kgm passes over a frictionless light pulley fixed on the top of a frictionless inclined plane which makes an angle of 30∘ with the horizontal. Masses m and M are tied at the two ends of wire such that m rests on the plane and M hangs freely vertically downwards. the entire system is in equilibrium and a transverse wave propagates along the wire with a velocities of 100m/s.View SolutionQuestion 138
Statement I:In a progressive logitudinal wave, the amplitude of the wave will not be the same at all points of the medium along the direction of motion of the wave.
Statement II: there is a continuous change of the phase angle of the wave as it progressive in the direction of motion. View SolutionQuestion 140
Statement I: two waves moving in a uniform string having uniform tension cannot have different velocities.
Elastic and inertial properties of string are same for all waves in same string. Moreover speed of wave in a string depends on its elastic and inertial properties only.View SolutionQuestion 148
A long string having a cross- sectional area 0.80mm2 and density 12.5gcm−3 is subjected to a tension of 64 N along the X-axis. One end of this string is attached to a vibrator moving in transverse direction at a frequency fo 20Hz. At t = 0. the source is at a maximujm displacement y= 1.0 cm. (a) Write the equation for the wave. (b) What is the displacement of the particle of the string at x = 50 cm at time t = 0.05 s ? (c) What is the velocity of this particle at this instant ?View SolutionQuestion 149
A long string having a cross- sectional area 0.80mm2 and density 12.5gcm−3 is subjected to a tension of 64 N along the X-axis. One end of this string is attached to a vibrator moving in transverse direction at a frequency fo 20Hz. At t = 0. the source is at a maximujm displacement y= 1.0 cm. (a) Write the equation for the wave. (b) What is the displacement of the particle of the string at x = 50 cm at time t = 0.05 s ? (c) What is the velocity of this particle at this instant ?View SolutionQuestion 150
A long string having a cross- sectional area 0.80mm2 and density 12.5gcm−3 is subjected to a tension of 64 N along the X-axis. One end of this string is attached to a vibrator moving in transverse direction at a frequency fo 20Hz. At t = 0. the source is at a maximujm displacement y= 1.0 cm. (a) Write the equation for the wave. (b) What is the displacement of the particle of the string at x = 50 cm at time t = 0.05 s ? (c) What is the velocity of this particle at this instant ?View SolutionQuestion 151
A long string having a cross- sectional area 0.80mm2 and density 12.5gcm−3 is subjected to a tension of 64 N along the X-axis. One end of this string is attached to a vibrator moving in transverse direction at a frequency fo 20Hz. At t = 0. the source is at a maximujm displacement y= 1.0 cm. (a) Write the equation for the wave. (b) What is the displacement of the particle of the string at x = 50 cm at time t = 0.05 s ? (c) What is the velocity of this particle at this instant ?View SolutionQuestion 156
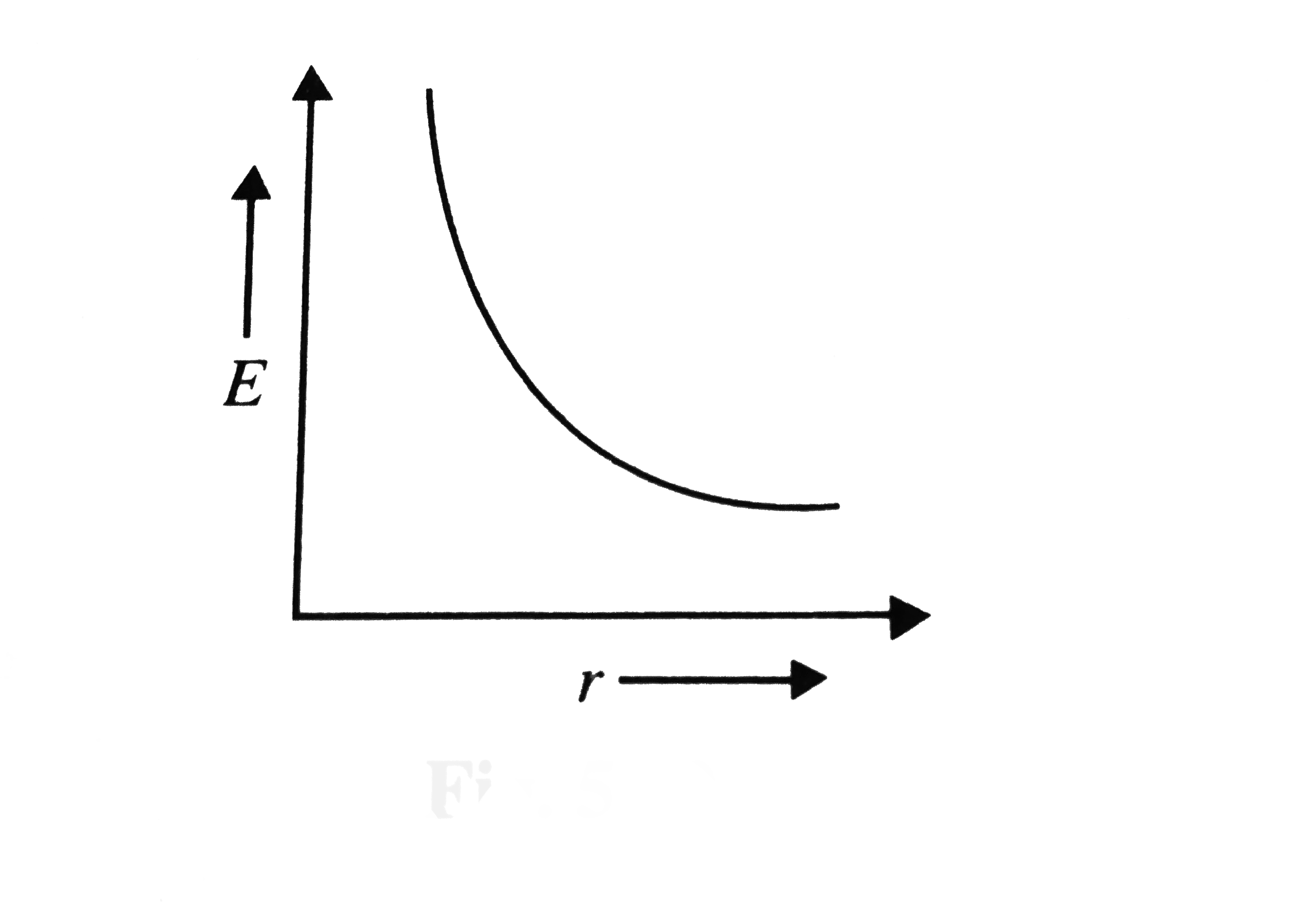
A plane wave propagates along positive x-direction in a homogeneous medium of density p=200kg/m3. Due to propagation of the wave medium particle oscillate. Space density of their oscillation energy is E=0.16π2J/m3 and maximum shear strain produced in the mendium is ϕ0=8π×10−5. if at an instant, phase difference between two particles located at points (1m,1m,1m) and (2m,2m,2m,) is Δθ=144∘, assuming at t=0 phase of particle at x=0 to be zero,
Wave velocity is View SolutionQuestion 157
A plane wave propagates along positive x-direction in a homogeneous medium of density p=200kg/m3. Due to propagation of the wave medium particle oscillate. Space density of their oscillation energy is E=0.16π2J/m3 and maximum shear strain produced in the mendium is ϕ0=8π×10−5. if at an instant, phase difference between two particles located at points (1m,1m,1m) and (2m,2m,2m,) is Δθ=144∘, assuming at t=0 phase of particle at x=0 to be zero,
wave length is View SolutionQuestion 158
A plane wave propagates along positive x-direction in a homogeneous medium of density p=200kg/m3. Due to propagation of the wave medium particle oscillate. Space density of their oscillation energy is E=0.16π2J/m3 and maximum shear strain produced in the mendium is ϕ0=8π×10−5. if at an instant, phase difference between two particles located at points (1m,1m,1m) and (2m,2m,2m,) is Δθ=144∘, assuming at t=0 phase of particle at x=0 to be zero,
Equation of wave is View SolutionQuestion 159
A sinusoidal wave is propagating in negative x-direction in a string stretched along x-axis. A particle of string at x=2 cm is found at its mean position and it is moving in positive y-direction at t=1 s. the amplitude of the wave, the wavelength and the angular frequency of the wave are 0.1m,π/4m and 4πrad/s, respectively.
The equation of the wave is View SolutionQuestion 160
A sinusoidal wave is propagating in negative x-direction in a string stretched along x-axis. A particle of string at x=2 cm is found at its mean position and it is moving in positive y-direction at t=1 s. the amplitude of the wave, the wavelength and the angular frequency of the wave are 0.1m,π/4m and 4πrad/s, respectively.
The speed of particle at x=2m and t=1s is View SolutionQuestion 161
A sinusoidal wave is propagating in negative x-direction in a string stretched along x-axis. A particle of string at x=2 cm is found at its mean position and it is moving in positive y-direction at t=1 s. the amplitude of the wave, the wavelength and the angular frequency of the wave are 0.1m,π/4m and 4πrad/s, respectively.
The equation of the wave is
The speed of particle at x=2m and t=1s is
The instantaneous power transfer through x=2m and t=1.125s is View SolutionQuestion 162
Four pieces of string of length L are joined end to end to make a long string of length 4L. The linear mass density of the strings are μ,4μ,9μand16μ, respectively. One end of the combined string is tied to a fixed support and a transverse wave has been generated at the other end having frequency f (ignore any reflection and absorption). string has been stretched under a tension F. Find the time taken by wave to reach from source end to fixed end.
View SolutionQuestion 163
Four pieces of string of length L are joined end to end to make a long string of length 4L. The linear mass density of the strings are μ,4μ,9μand16μ, respectively. One end of the combined string is tied to a fixed support and a transverse wave has been generated at the other end having frequency f (ignore any reflection and absorption). string has been stretched under a tension F.
Find the ratio of wavelength of the wave on four string, starting from right hand side.View SolutionQuestion 164
figure. Shows a student setting up wave wave on a long stretched string. The student's hand makes one complete up and down movement in 0.4s and in each up and down movement the hand moves by a height of 0.3m. The wavelength of the waves on the string is 0.8m.
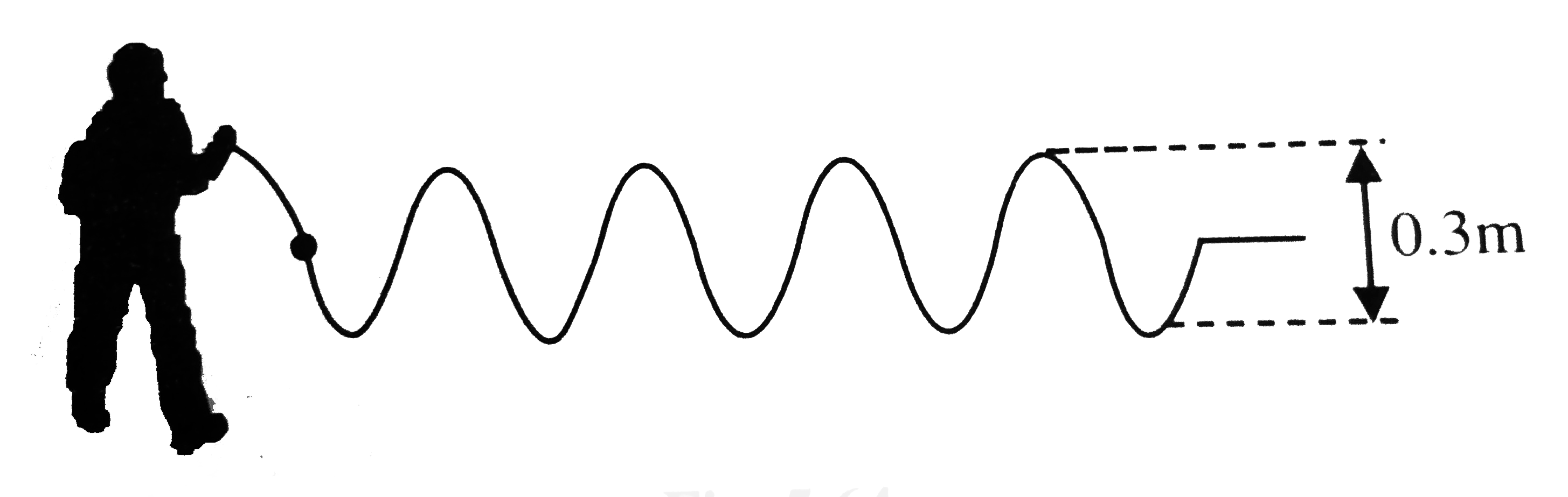
The frequency of the wave is View SolutionQuestion 165
figure. Shows a student setting up wave wave on a long stretched string. The student's hand makes one complete up and down movement in 0.4s and in each up and down movement the hand moves by a height of 0.3m. The wavelength of the waves on the string is 0.8m.
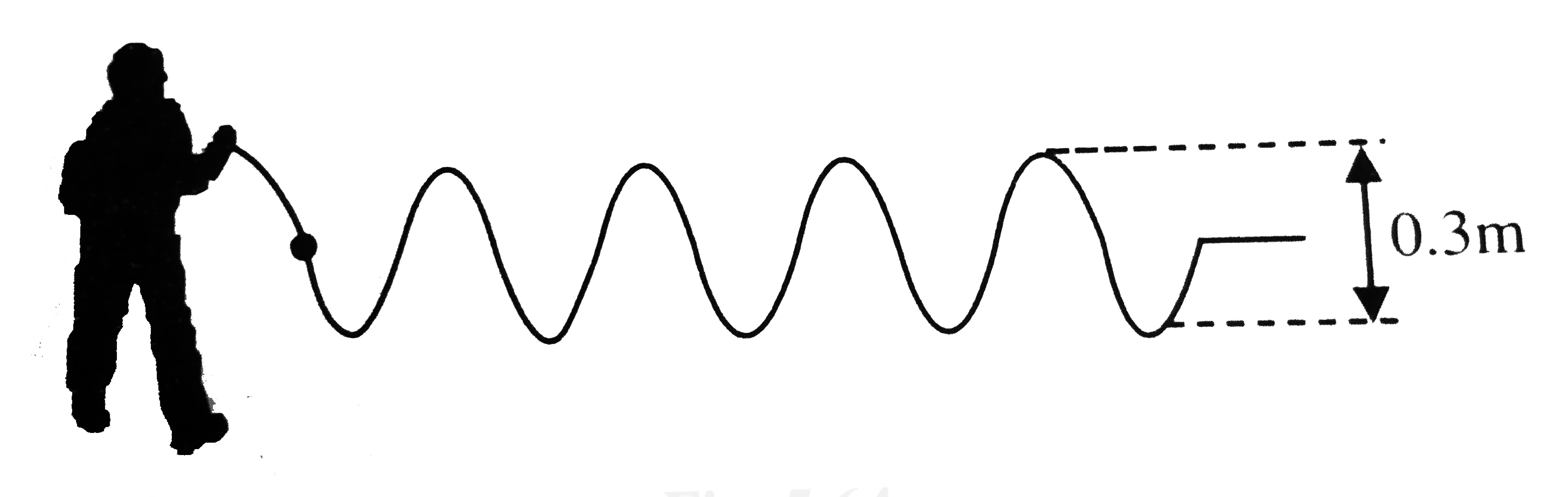
The amplitude of the wave is View SolutionQuestion 166
figure. Shows a student setting up wave wave on a long stretched string. The student's hand makes one complete up and down movement in 0.4s and in each up and down movement the hand moves by a height of 0.3m. The wavelength of the waves on the string is 0.8m.
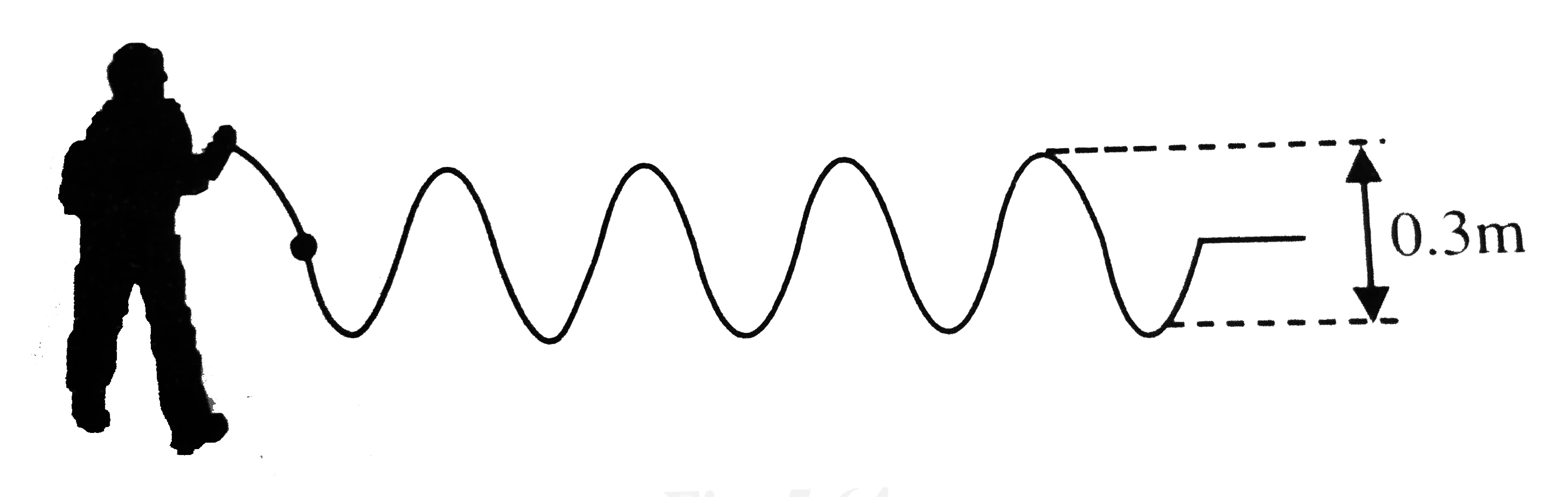
The wave speed is View SolutionQuestion 167
A child playing with a long rope ties one end holds the other. The rope is stretched taut along the horizontal. The child shakes the end he is holding, up and down, in a sinusoidal manner with amplitude 10cm and frequency 3 Hz.
Speed of the wave is 15m/s and, at t=0, displacement at the child's end is maximum positive. Assuming that there is no wave reflected from the fixed end, so that the waves in the rope are plane progressive waves, answer the following quetions.
(Also assume that the wave propagates along the positive x−direction.)
A wave function that describe the wave in the given sutuation is View SolutionQuestion 168
A child playing with a long rope ties one end holds the other. The rope is stretched taut along the horizontal. The child shakes the end he is holding, up and down, in a sinusoidal manner with amplitude 10cm and frequency 3 Hz.
Speed of the wave is 15m/s and, at t=0, displacement at the child's end is maximum positive. Assuming that there is no wave reflected from the fixed end, so that the waves in the rope are plane progressive waves, answer the following quetions.
(Also assume that the wave propagates along the positive x−direction.)
A wave function that describe the wave in the given sutuation is View SolutionQuestion 169
A child playing with a long rope ties one end holds the other. The rope is stretched taut along the horizontal. The child shakes the end he is holding, up and down, in a sinusoidal manner with amplitude 10cm and frequency 3 Hz.
Speed of the wave is 15m/s and, at t=0, displacement at the child's end is maximum positive. Assuming that there is no wave reflected from the fixed end, so that the waves in the rope are plane progressive waves, answer the following quetions.
(Also assume that the wave propagates along the positive x-direction.)
Phase difference between the child,s end and a point 2.5m from the child's end will be View SolutionQuestion 170
One end of a long rope is tied to a fixed vertical pole. The rope is stretched horizontally with a tension 8N . Let us cinsider the length of the rope to be along x-axis. A simple harmonic oscillator at x=0 generates a transverse wave of frequency 100Hz and amplitude 2cm along the rope. Mass of a unit length of the rope is 20g/m. ignoring the effect of gravity, answer the following quetions.
Tension in the given rope remaining the same, if a simple harmonic oscillator of frequency 200Hz is used instead of the earlier oscillator of frequency 100Hz View SolutionQuestion 171
One end of a long rope is tied to a fixed vertical pole. The rope is stretched horizontally with a tension 8N . Let us cinsider the length of the rope to be along x-axis. A simple harmonic oscillator at x=0 generates a transverse wave of frequency 100Hz and amplitude 2cm along the rope. Mass of a unit length of the rope is 20g/m. ignoring the effect of gravity, answer the following quetions.
Tension in the given rope remaining the same, if a simple harmonic oscillator of frequency 200Hz is used instead of the earlier oscillator of frequency 100Hz View SolutionQuestion 172
One end of a long rope is tied to a fixed vertical pole. The rope is stretched horizontally with a tension 8N . Let us cinsider the length of the rope to be along x-axis. A simple harmonic oscillator at x=0 generates a transverse wave of frequency 100Hz and amplitude 2cm along the rope. Mass of a unit length of the rope is 20g/m. ignoring the effect of gravity, answer the following quetions.
Tension in the given rope remaining the same, if a simple harmonic oscillator of frequency 200Hz is used instead of the earlier oscillator of frequency 100Hz View SolutionQuestion 173
One end of a long rope is tied to a fixed vertical pole. The rope is stretched horizontally with a tension 8N . Let us cinsider the length of the rope to be along x-axis. A simple harmonic oscillator at x=0 generates a transverse wave of frequency 100Hz and amplitude 2cm along the rope. Mass of a unit length of the rope is 20g/m. ignoring the effect of gravity, answer the following quetions.
maximum magnitude of transverse acceleration of any point on the rope will be nearly View SolutionQuestion 174
One end of a long rope is tied to a fixed vertical pole. The rope is stretched horizontally with a tension 8N . Let us cinsider the length of the rope to be along x-axis. A simple harmonic oscillator at x=0 generates a transverse wave of frequency 100Hz and amplitude 2cm along the rope. Mass of a unit length of the rope is 20g/m. ignoring the effect of gravity, answer the following quetions.
Tension in the given rope remaining the same, if a simple harmonic oscillator of frequency 200Hz is used instead of the earlier oscillator of frequency 100Hz View SolutionQuestion 175
A rope is attached at one end to a fixed vertical pole . It is stretched horizontal with a fixed value of tension T . Suppose at t=0, a pulse is generated by moving the free end of the rope up and down once with your hand. The pulse arrives at the pole at instant t.
Ignoring the effect of gravity, answer the following quetions.
A.. If you move your hand up and down once but to a greater distance and in the same amount of time. View SolutionQuestion 176
A rope is attached at one end to a fixed vertical pole . It is stretched horizontal with a fixed value of tension T . Suppose at t=0, a pulse is generated by moving the free end of the rope up and down once with your hand. The pulse arrives at the pole at instant t.
Ignoring the effect of gravity, answer the following quetions.
If you move your hand up and down once by the same amount but do it more rapidly, say, twice as fast as in the earlier case.View SolutionQuestion 177
A rope is attached at one end to a fixed vertical pole . It is stretched horizontal with a fixed value of tension T . Suppose at t=0, a pulse is generated by moving the free end of the rope up and down once with your hand. The pulse arrives at the pole at instant t.
Ignoring the effect of gravity, answer the following quetions.
If you use a string of same length but of greater mass View SolutionQuestion 178
A rope is attached at one end to a fixed vertical pole . It is stretched horizontal with a fixed value of tension T . Suppose at t=0, a pulse is generated by moving the free end of the rope up and down once with your hand. The pulse arrives at the pole at instant t.
Ignoring the effect of gravity, answer the following quetions.
In all the above, quetions we have considered a fixed value of tension. however, if tension in a given rope is increased and a pulse is genrated as described,View SolutionQuestion 181
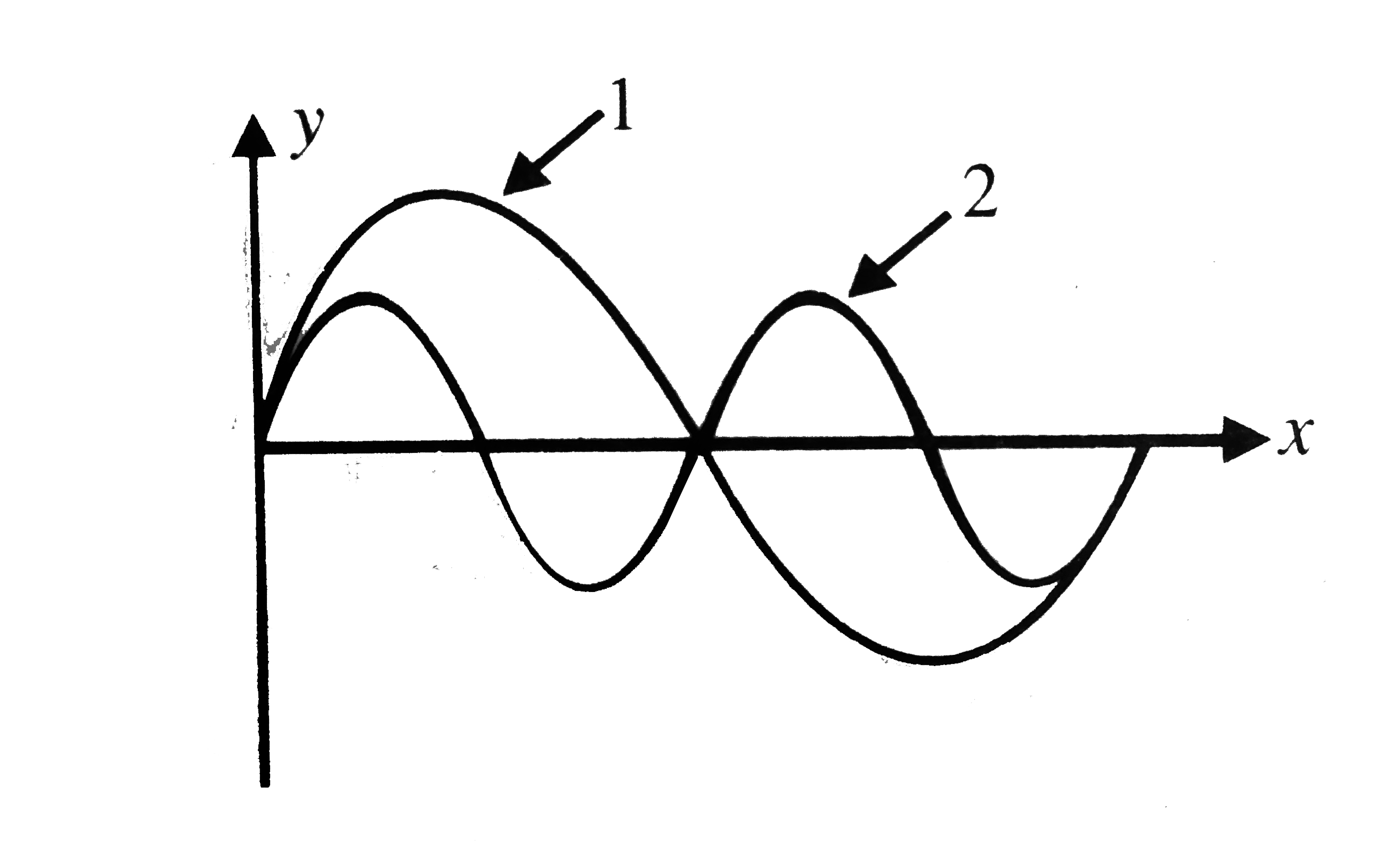
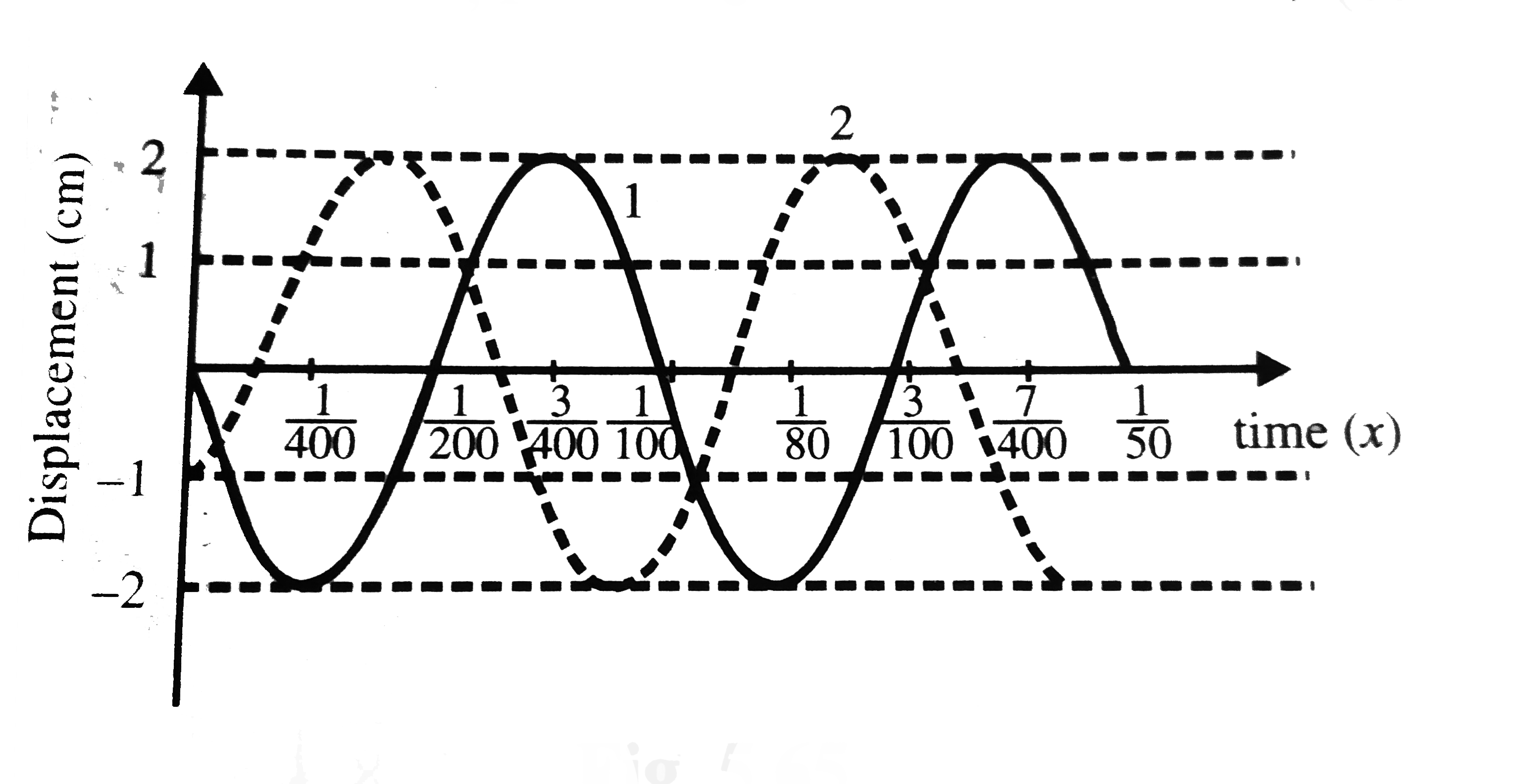
Figure. shows two snapshots of medium particle supporting a plane progressive wave travelling along positive x−axos, corresponding to instants t=0.002s and t=0.008s, respectively shown by curves numbered 1 and 2.
Assume that the interval between the two snapshots is less than the time period. Velocity of the wave is
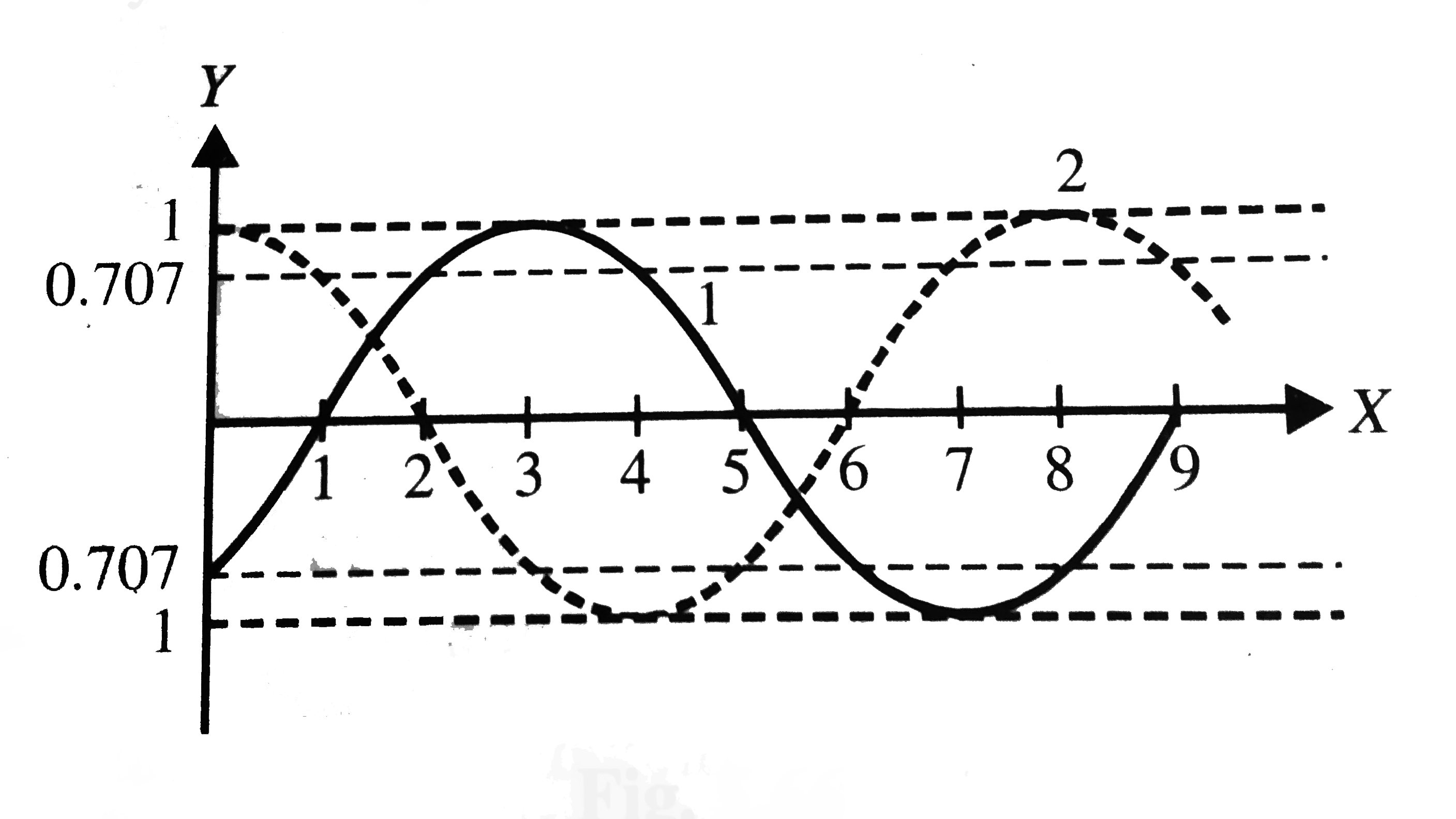
View SolutionQuestion 182
Figure .shows two snapshots of medium particle supporting a plane progressive wave travelling along positive x-axos, corresponding to instants t=0.002s and t=0.008s, respectively shown by curves numbered 1 and 2.
Assume that the interval between the two snapshots is less than the time period.The frequency of the wave
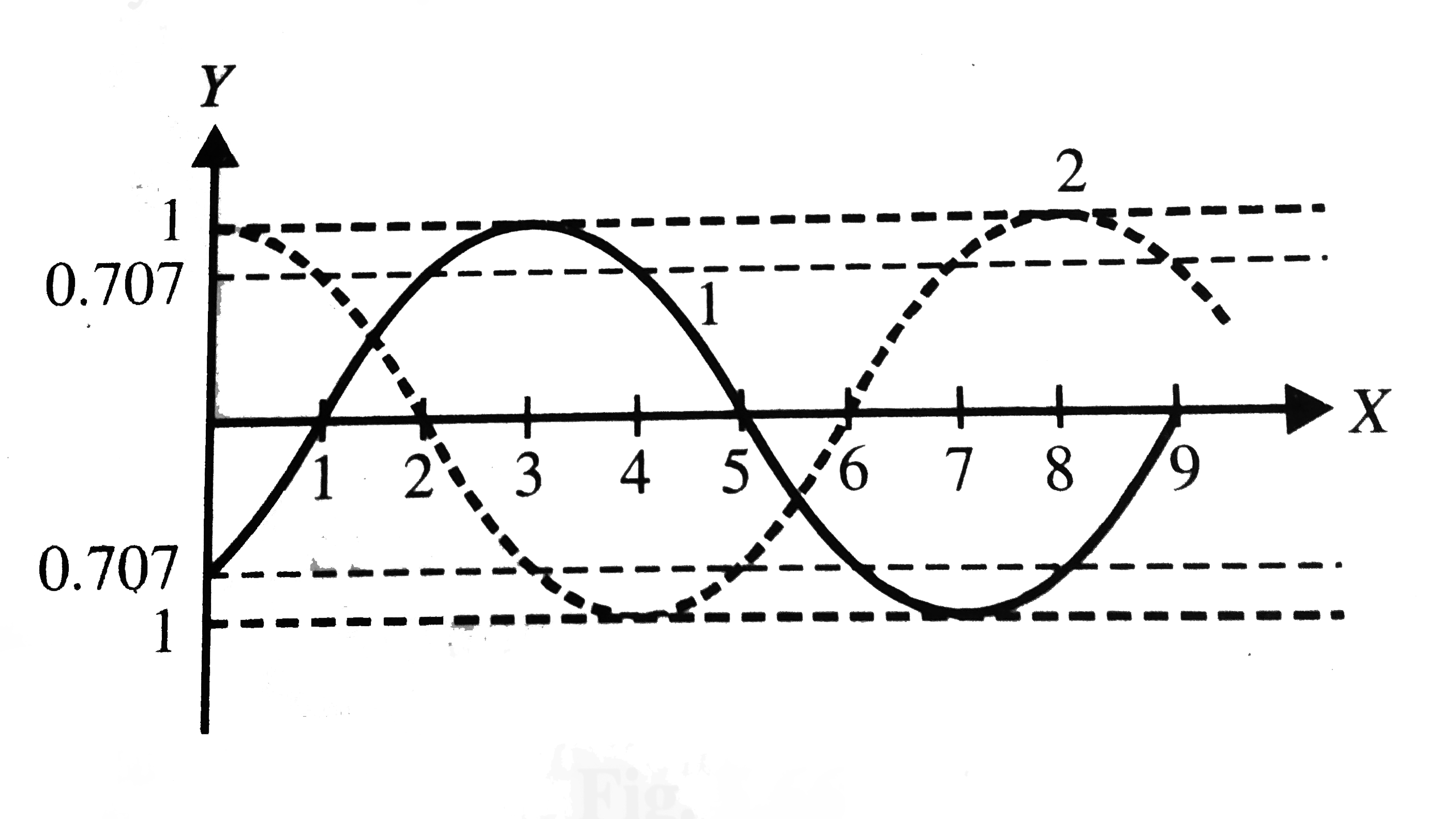
View SolutionQuestion 183
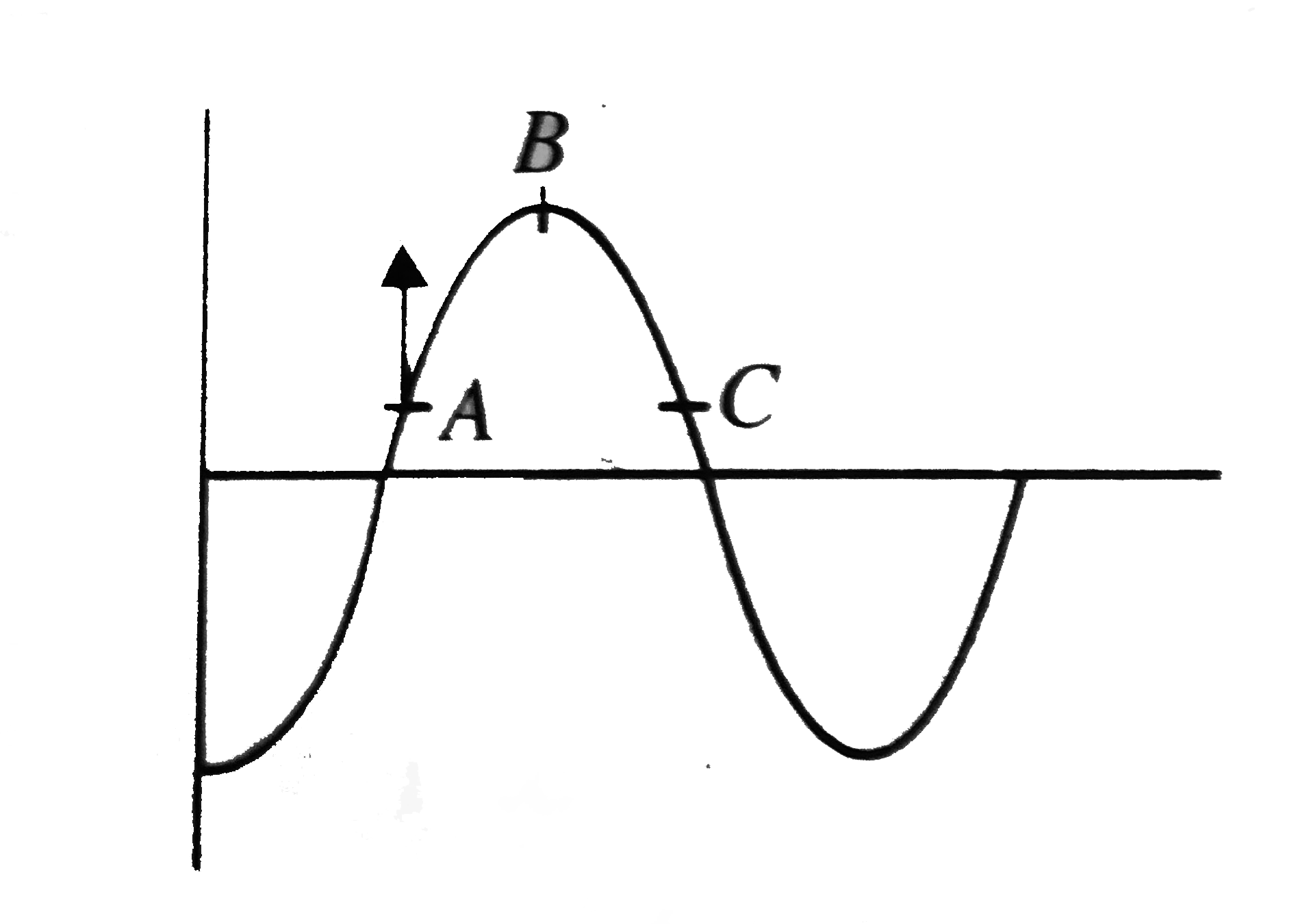
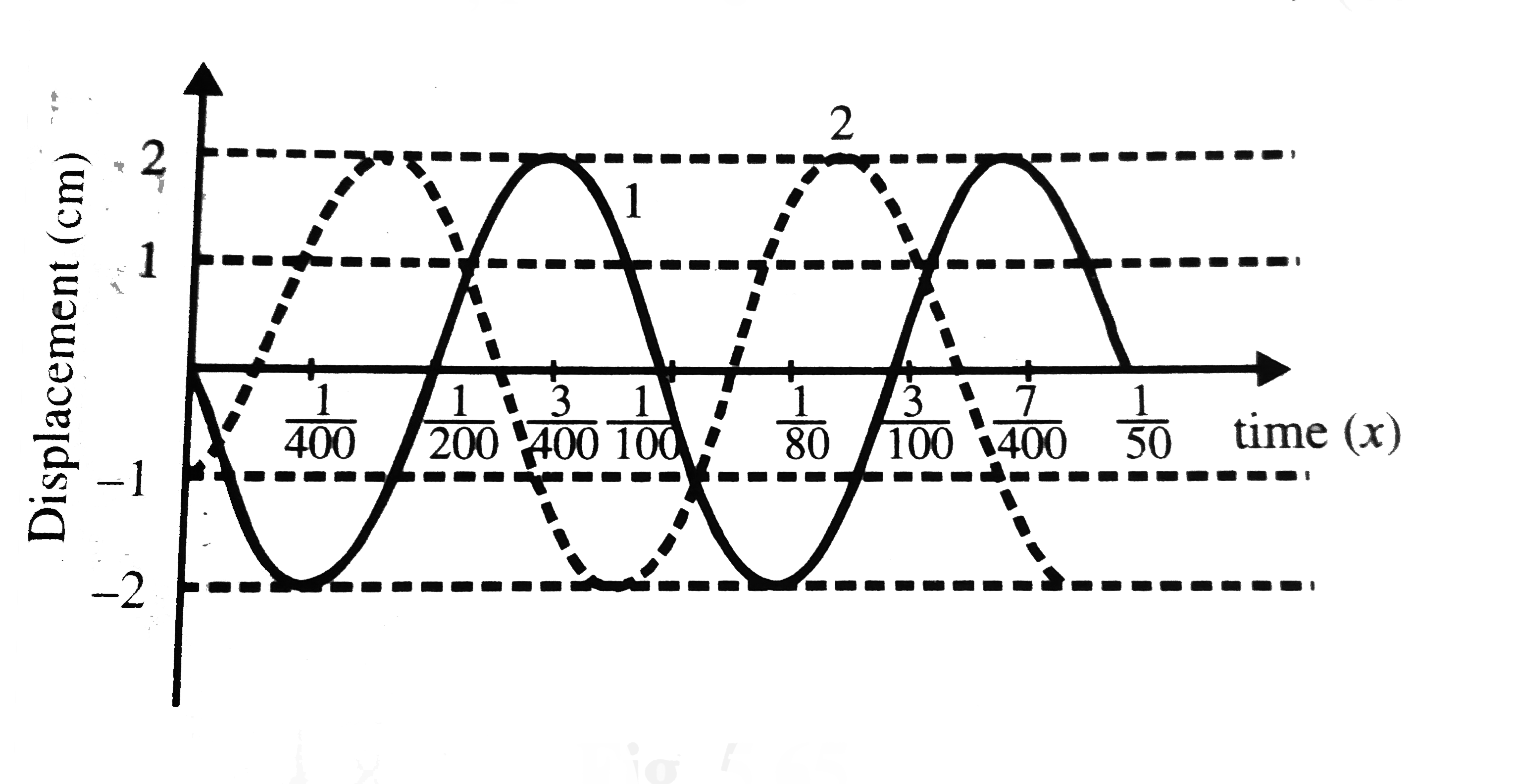
The figure shows a snap photograph of a vibrating string at t=0. The particle P is observed moving up with velocity 20√3cm/s. The tangent at P makes an angle 60∘ with x-axis.
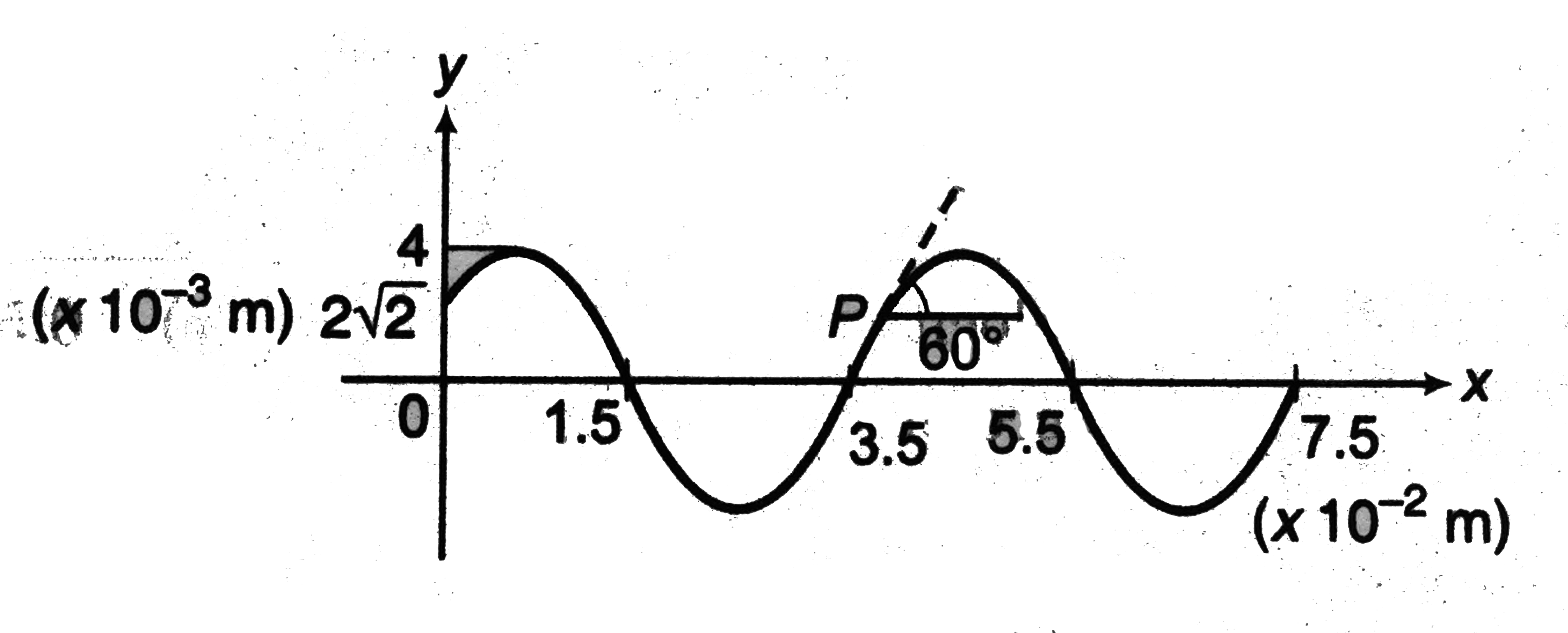
(a) Find the direction in which the wave is moving.
(b) Write the equation of the wave.
(c) The total energy carries by the wave per cycle of the string. Assuming that the mass per unit length of the string is 50g/m.View SolutionQuestion 184
The figure shows a snap photograph of a vibrating string at t=0. The particle P is observed moving up with velocity 20√3cm/s. The tangent at P makes an angle 60∘ with x-axis.
(a) Find the direction in which the wave is moving.
(b) Write the equation of the wave.
(c) The total energy carries by the wave per cycle of the string. Assuming that the mass per unit length of the string is 50g/m.View SolutionQuestion 185
A pulse is started at a time t=0 along the +xdirection on a long, taut string. The shape of the pulse at t=0 is given by function f(x) with {x−vt4+1forvt−4<x≤vt−(x−vt)+1forvt<x<vt+1
0, otherwise
here f and x are in centimeters. The linear mass density of the string is 50g/m and it is under a tension of 5N.
C..The transverse velocity of the particle at x=13cm and t=0.015s will be View SolutionQuestion 186
A pulse is started at a time t=0 along the +xdirection on a long, taut string. The shape of the pulse at t=0 is given by function f(x) with {x−vt4+1forvt−4<x≤vt−(x−vt)+1forvt<x<vt+1
0, otherwise
here f and x are in centimeters. The linear mass density of the string is 50g/m and it is under a tension of 5N.
C..The transverse velocity of the particle at x=13cm and t=0.015s will be View SolutionQuestion 187
A pulse is started at a time t=0 along the +xdirection on a long, taut string. The shape of the pulse at t=0 is given by function f(x) with
here f and x are in centimeters. The linear mass density of the string is 50g/m and it is under a tension of 5N.
The transverse velocity of the particle at x=13cm and t=0.015s will be View SolutionQuestion 191
A string of length 20 cm and linear mass density 0.4g/cm is fixed at both ends and is kept under a tension of 16 N. A wave pulse is produced at t=0 near an end as shown in figure which travels towards the other end. (a) When will the string have the shape shown in the figure again? (b) Sketch the shape of the string at a time half of that found in part (a).
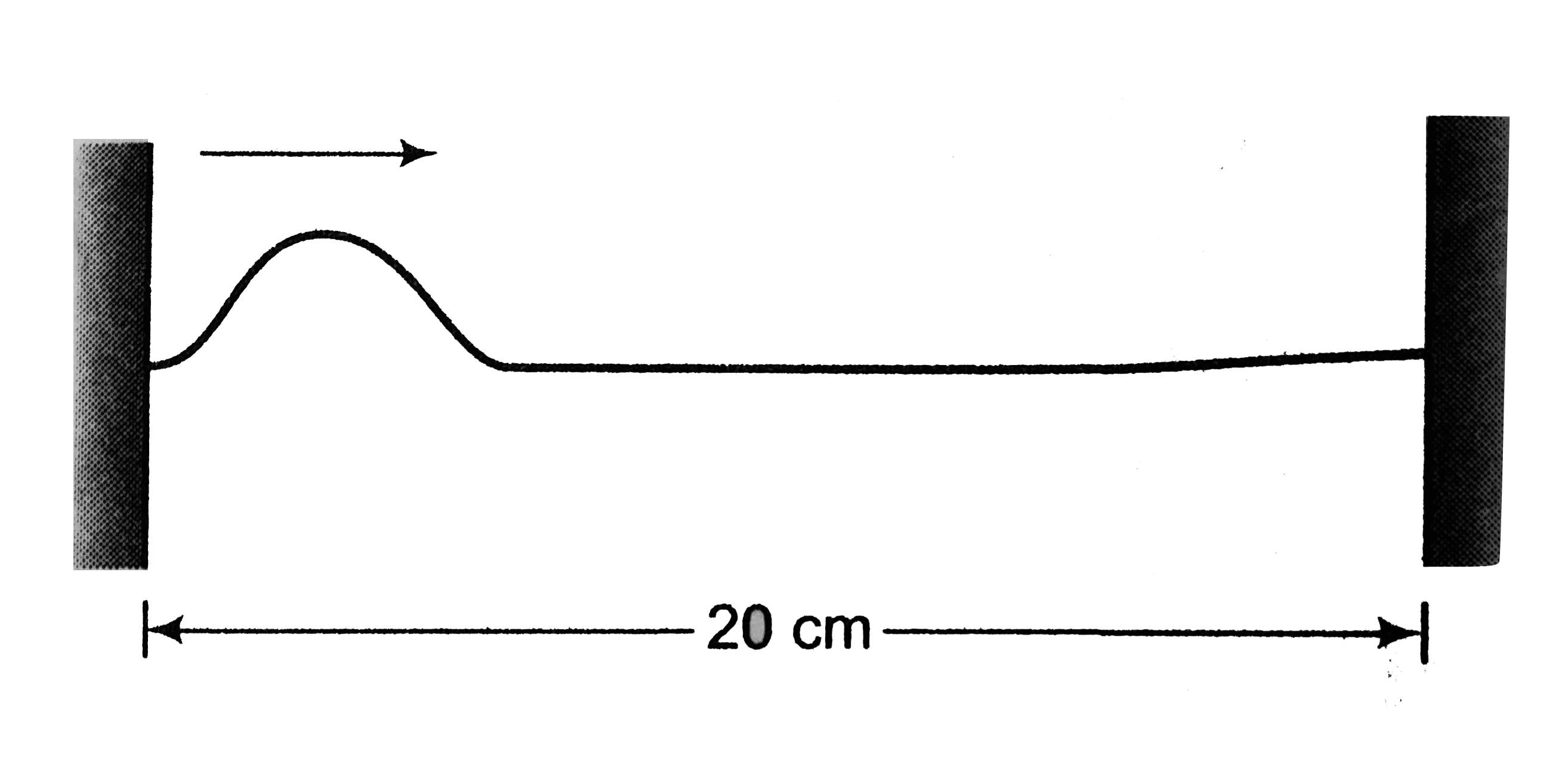View SolutionQuestion 192
A string of length 40 cm and weighing 10 g is attached to a spring at one end and to a fixed wall at the other end. The spring has a spring constant of 160Nm−1 and is stretched by 1.0 cm. If a wave pulse is produced on the string near the wall, how much time will it take to reach the spring ? View SolutionQuestion 193
A 4.0 kg block is suspended from the ceiling of an elevator through a string having a linear mass desity of 19.2×10−3kgm−1. Find the speed (with respect to the string) with which a wave pulse can proceed on the string if the elavator accelerates up at the rate of 2.0ms−2.Takeg=10ms−2.View SolutionQuestion 196
An ant with mass m is standing peacefully on top of a horizontal, stretched rope. The rope has mass per unit length μ and is under tension F. Without warning, a student starts a sinusoidal transverse wave of wavelength λ propagating along the rope. the motion of the rope is in a verticle plane. what minimum wave amplitude (in mm) will make the ant feel weightless momentarily? Assume that m is so small that the presence of the ant has no effect on the propagation of the wave.
[Given: λ=0.5m,μ=0.1kg/m,F=3.125N,takeg=π2]View Solution
