Exercise from DHANPAT RAI & CO PHYSICS Chapter 3 GRAVITATION for Class 11
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| DHANPAT RAI & CO PHYSICS | Exercise |
| Medium | English |
| Academic Year | 2023-2024 |
Question 8
In an experiment using the Cavendish balance , the smaller spheres have a mass of 20 kg each , the larger spheres have a mass 5 kg each , the length of the rod is 50.0 cm the torsion constant of the fibre is 4.8×10−8 Nm per radian , the angle of twist is 7×10−3 rad , and the distance between the centres of each pair of heavy and light spheres is 100 cm . Compute the value of the gravitational constant G from this data . View SolutionQuestion 23
The weight of a person on the Earth is 80kgwt. What will be his weight on the Moon ? Mass of the Moon =7.34×1022kg, radius =1.75×106m and gravitational constant =6.67×10−11Nm2kg−2. What will be the mass of the person at the Moon and acceleration due to gravity there ? If this person can jump 2m high on the Earth, how much high can he jump at the Moon ?View SolutionQuestion 63
A satellite orbits the earth at a height of 400 km, above the surface. How much energy must be expended to rocket the satellite out of the earth's gravitational influence ? Mass of the satellite=200 kg, mass of the earth=6.0×1024kg, radius of the earth=6.4×10(6)m, G=6.67×10−11Nm2Kg−2.View SolutionQuestion 76
A solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m isView SolutionQuestion 143
A synchronous satellite goes around the earth one in every 24 h. What is the radius of orbit of the synchronous satellite in terms of the earth's radius ? (Given: Mass of the earth , ME=5.98×1024kg, radius of the earth, RE=6.37×106m, universal constant of gravitational , G=6.67×10−11Nm2kg−2) View SolutionQuestion 213
STATEMENT -1 : In absence of air friction, it is claimed that all object fall with the same acceleration although, a heavier object is pulled towards the earth with more force than a lighter object.
because
STATEMENT-2 : Net external force is always equal to rate of change of linear momentum. View SolutionQuestion 324
A block hole is a body from whose surface nothing may even escape. What is the condition for a uniform spherical body of mass M to be a block hole? What should be the radius of such a black hole if its mass is nine times the mass of the earth?
Mass of earth =6×1024kg,
G=6.61×10−11Nm2kg−2.View SolutionQuestion 336
Obtain an expression for the acceleration due to gravity on the surface of the earth in terms of mass of the earth and its radius. Discuss the variation of acceleration due to gravity with altitude and depth. If a body is taken to a height R / 4 from the surface of the earth, find percentage decrease in the weight of the body ? Here R is the radius of the earth.View SolutionQuestion 354
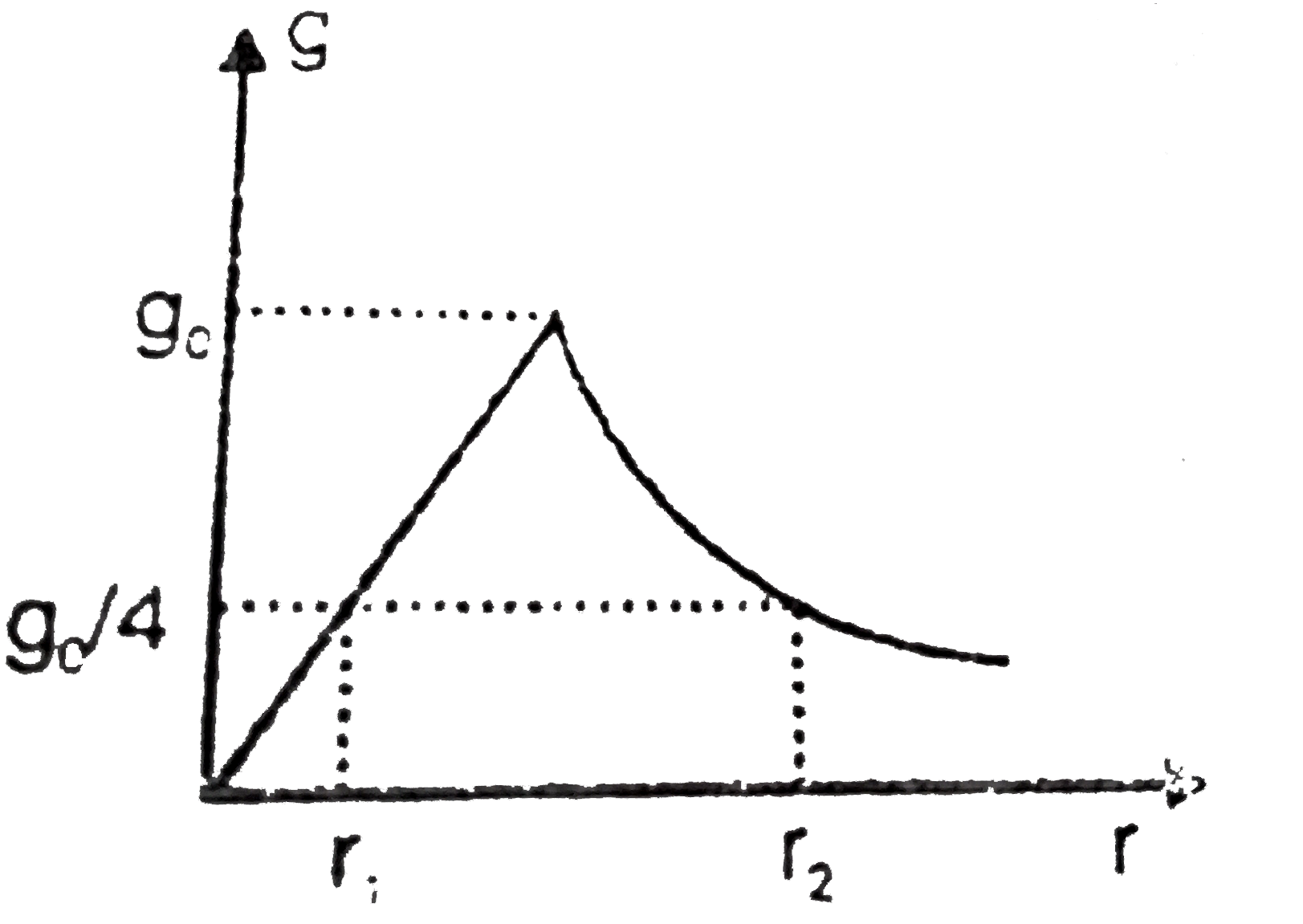
A spherically symmetric gravitational system of particles has a mass densityρ={ρ0forr<R0forr>R whereρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0<r<OO) form the centre of the system is represented byView SolutionQuestion 355
A planet of radius R=110×(radiusofEarth) has the same mass density as Earth. Scientists dig a well of depthR5 on it and lower a wire of the same length and a linear mass density 10−3kgm(_1) into it. If the wire is not touching anywhere, the force applied at the top of the wire by a person holding it inplace is (take the radius of Earth=6×106m and the acceleration due to gravity on Earth is 10ms−2View SolutionQuestion 357
A rocket is launched normal to the surface of the earth, away from the sun, along the line joining the sun and the earth. The sun is 3×105 times heavier than the earth and is at a distance 2.5×104 times larger than the radius of the earth. the escape velocity from earth's gravitational field is ue=11.2kms−1. The minmum initial velocity (ue)=11.2kms−1. the minimum initial velocity (us) required for the rocket to be able to leave the sun-earth system is closest to (Ignore the rotation of the earth and the presence of any other planetView SolutionQuestion 359
A solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
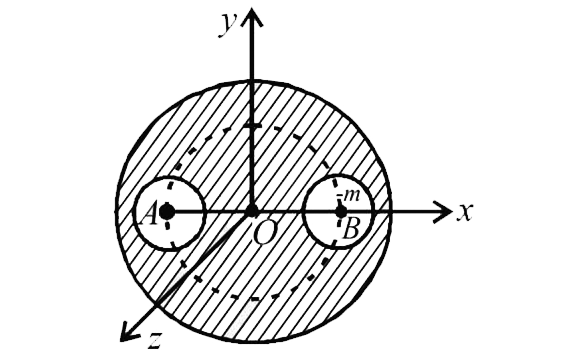 View Solution
View SolutionQuestion 367
Two spherical bodies of mass M and 5M & radii R & 2R respectively are released in free space with initial separation between their centres equal to 12R. If they attract each other due to gravitational force only, then the distance covered by the smallar body just before collision is View SolutionQuestion 386
A very long (length L) cylindrical galaxy is made of uniformly distributed mass and has radius R (R<<L) A star outside the galaxy is orbiting the galaxy in a plane perpendicular to the galaxy and passing through its centre. If the time period of star is T and its distance from the galaxy's axis is r, then-View SolutionQuestion 387
A satellite is revolving in a circular orbit at a height 'h' from the earth's surface (radius of earth R, h ltltR). The minimum increase in its orbital velocity required, So that the satellite could escape from the erth's gravitational field, is close to :(Neglect the effect of atomsphere.)View SolutionQuestion 389
_E01_134_Q01.png)
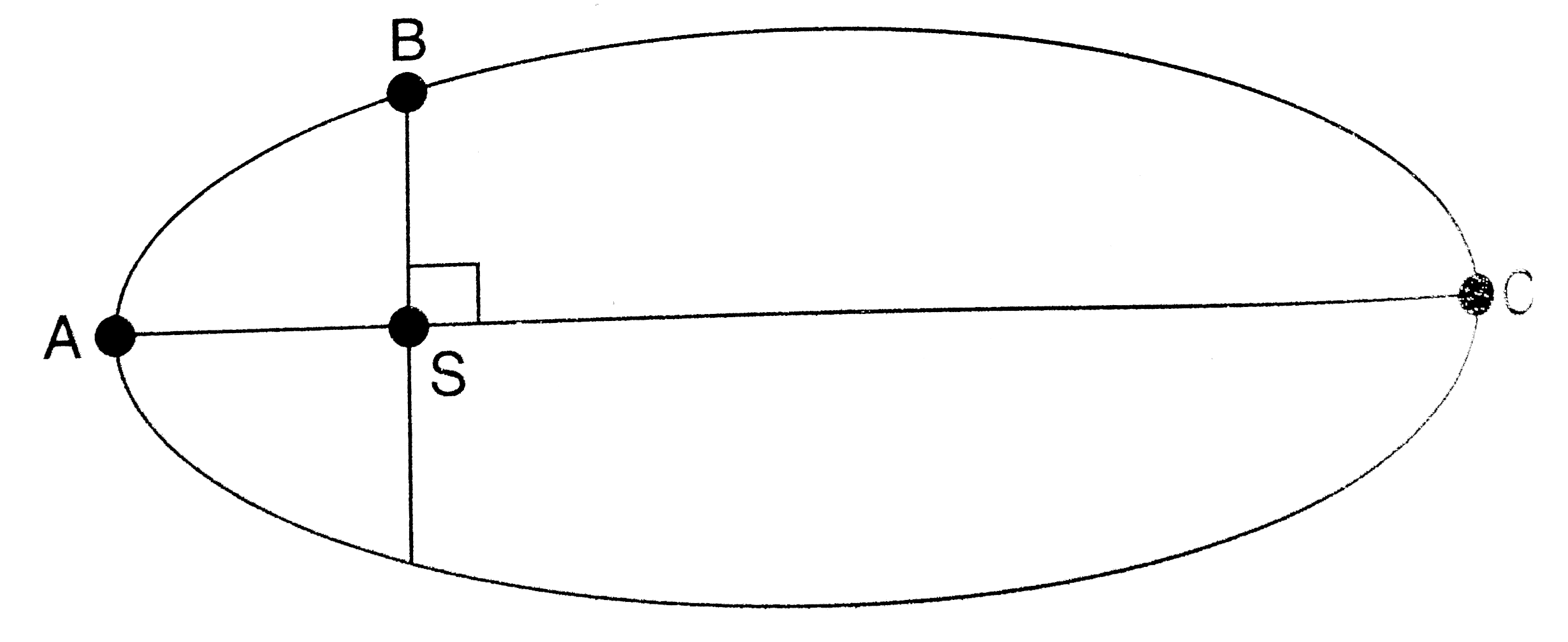
Figure elliptical path abcd of a planet around the sun S such that the area of Delta csa is 14 the area of the ellipse, (see figure) with db as the semimajor axis, and ca as the semiminor axis if t1 is the time taken for planet to go over path abc and t2 for path taken over cda then:View SolutionQuestion 402
The value of ‘ g ’ at a particular point is 9.8m/s2 . Suppose the earth suddenly shrinks uniformly to half its present size without losing any mass. The value of ‘ g ’ at the same point (assuming that the distance of the point from the centre of earth does not shrink) will now beView SolutionQuestion 453
A particle of mass m is thrown upwards from the surface of the earth, with a velocity u. The mass and the radius of the earth are, respectively, M and R. G is gravitational constant g is acceleration due to gravity on the surface of earth. The minimum value of u so that the particle does not return back to earth is View SolutionQuestion 472
Kepler's third law states that square of period revolution (T) of a planet around the sun is proportional to third power of average distance i between sun and planet i.e. T2=Kr3
here K is constant
if the mass of sun and planet are M and m respectively then as per Newton's law of gravitational the force of alteaction between them is F=GMmr2, here G is gravitational constant. The relation between G and K is described as View Solution
All Exercises from DHANPAT RAI & CO PHYSICS Class 11 PHYSICS GRAVITATION
- Based on Acceleration due to gravity
- Based on Variation of g with Altitude
- Based on Variation of g with Depth
- Based on Variation of g with Rotation of the earth
- Example
- Exercise
- G :Based on Orbital Velocity of Satellites
- H: Based on Escape Velocity
- I: Based on Kepler s Law of Periods
- J: Based on Gravitational Intensity, Potential and Potential Energy
- Problem From Competitive Examinations
- m




_S01_025_Q01.png)