EXERCIESE from HC VERMA PHYSICS (HINGLISH) HEAT TRANSFER for Class 11

Class 11	PHYSICS
Chapter	HEAT TRANSFER
HC VERMA PHYSICS (HINGLISH)	EXERCIESE
Medium	English
Academic Year	2023-2024

Question 1
A uniform slab of dimension $10 c m \times 10 c m \times 1 c m$ is kept between two heat reservoire at temperatures $10^{\circ} C and$ 90^(@)C $T h e l a r \geq r s u r f a c e a r e a s \to u c h t h e r e s e r v o i r s . T h e t h e r m a l c o n d u t i v i t y o f t h e m a t e r i a l i s$ 0.80Wm^(-1) $^(\circ) C^{- 1}$ . Find the amount of heat flowing through the slab per minute. View Solution
Question 2
A liquid-nitrogen container is made of a $1 - c m$ thick styrofoam sheet having thermal conductivity $0.025 J s^{- 1} m^{- 1}$ ^(@)C^(1) $. L i q u i t r o \geq n a t 80 K i s k e p t \in i t . A \to t a l a r e a o f$ 0.80m^(-2) $i s \in c o n t c e t w i t h t h e l i q u i t r o \geq n . T h e a t m o s p h e r i c t e m p e r a t u r e i s$ 300K . Calculate the rate of heat flow from the atmosphere to the liquid nitrogen. View Solution
Question 3
The normal body-temperature of a person is $97 (\circ) F$ . Calculate the rate at which heat is flowing out of this body through the clothes asssuming the following values. Room temperature $= 47^{\circ} F$ , surface of the body under clothes $= 1.6 m^{- 2}$ , condutivity of the cloth $= 0.04 J s^{- 1} m^{- 1}$ ^(@)C^(-1) $, t h i c k \neq s s o f t h e c l o t h$ =0.5cm. View Solution
Question 4
Water is boiled in a container having a bottom of surface area $25 c m^{2}$ , thickness $1.0 m m and t h e r m a l c o n d u c t i v i t y$ 50Wm^(-1) $^(\circ) C^{- 1}$ , 100g of water is converted into steam per minute in the steady state after the boiling starts.Assuming that no heat is lost to the atmosphere, calculate the temperature of the lower surface of the bottom. Latent heat of vaporrization of water $= 2.26 \times 10^{6} J k g^{- 1}$ .View Solution
Question 5
One end of a steel rod $(K = 46 J s^{- 1} m^{- 1}$ ^(@)C^(-1) $o f \leq n > h$ 1.0m is kept in ice at $0^{\circ} C$ and the other end is kept in boiling water at 100^(@)C $. T h e a r e a o f c r o s s sec t i o n o f t h e r o d i s$ 0.04cm^(2) $. A s \sum \in g n o h e a t l o s s \to t h e a t m o s p h e r e, f \in d t h e m a s s o f t h e i c e m e < \in g p e r sec o n d . L a t e n t h e a t o f f u s i o n o f i c e$ =3.36xx10^(5)Jkg^(-1) .View Solution
Question 6
An icebox almost comletely filled with ice at $0^{\circ} C$ is dipped into a large volume of watert at $20^{\circ} C$ . The box has walls of surface area $2400 c m^{2}$ thickness $2.0 m m$ and thermal conductivity 0.06Wm^(-1) $^(\circ) C^{- 1}$ . Calculate the rate at which the ice melts in the box. Letent heat of fusion of ice $= 3.4 \times 10^{5} J k g^{- 1}$ .View Solution
Question 7
A pitcher with $1 - m m$ thick porous walls contain 10kg of water. ,Water comes to its outer surface and evaporates at the rate of $0.1 g s^{- 1}$ . The surface area of the pitcher (one side) $= 200 c m^{2}$ . The room temperature $= 42^{\circ} C$ , latent heat of vaporization $= 2.27 \times 10^{6} J k g^{- 1}$ , and the thermal conductivity of the porous walls $= 0.80 j s^{- 1} m^{- 1}$ ^(@)C^(-1) . Calculate the temperature of water in the pitcher when it attains a constant value. View Solution
Question 8
A steel farme $(K = 45 W m^{- 1}$ ^(@)C^(-1) $o f \to t a l \leq n > h$ 60cm $and c r o s s sec t i o n a r e a$ 0.02cm^(2) $, F or m s t h r e e s o f a □ . T h e e e e n d s a r e m a \int a \in e d a t$ 20^(@)C $and$ 40^(@)C . Find the rate of heat flow through a cross section of the frame. View Solution
Question 9
Water at $506 (\circ) C$ is filled in a closed cylindercal vessel of height $10 c m$ and cross sectional area $10 c m^{2}$ The walls of the vessel are adiabatic but the flat parts are made of $1 - m m$ thick aluminium $(K = 200 J s^{- 2} m^{- 1}$ ^(@)C^(-1) $. A s \sum e t ˆ t h e o u t s t e m p e r a t u r e i s$ 20^(@)C $. T h e d e n s i t y o f w a t e r i s$ 1000kgm^(-3) $and t h e s p e c if y h e a t \cap a c i t y o f w a t e r$ =4200Jkg^(-1) $^(\circ) C^{- 1}$ .Estimate the time taken for the temperature to fall by ${1.0}^{\circ} C$ . Make any simplifying assumotion you need but speify them.View Solution
Question 10
The lleft end of a copper rod $(\leq n > h = 20 c m . A r e a o f c r o s s sec t i o n = 0.02 c m^{2}$ is maintained at $20^{\circ} C$ and the right end is maintained at $80^{\circ} C$ . Neglecting any lkkoss of heat through radiation, find (a) the temperature at a point 11cm from the left end and (b) the heat current through the rod. thermal conductivity of copper $= 385 W m =^{- 1}$ ^(@)C^(-1) .View Solution
Question 11
The ends of a metre stick are maintain at $100^{\circ} C$ and $0^{\circ} C$ . One end of a rod is mainntained $25^{\circ} C$ . Where should its other end be touched on the metre stick so that there is no heat current in the rod in steady state?View Solution
Question 12
A cubical box of volume $216 c m^{3}$ is made up of $0.1 c m t h i c k w \infty d, T h e \in s i s h e a t e d e \leq c t r i c a l l y b y 100 W h e a t e r . I t i s f o u n d t ˆ t h e t e m p e r a t u r e d \Leftrightarrow e r e n c e b e t w e e n t h e \in s and t h e o u t s s u r f a c e$ 5^(@)C . In steady state . Assuming that the entire electrically energy spent appears as heat, find the thermal conductivity of the material of the box.View Solution
Question 13
Figure shows water in a container having $2.0 - m m$ thick walls made of a material of thermal conductivity $0.50 W m^{- 1}$ ^(@)C^(-1) $. T h e c o n t a \in e r i s k e p t \in a m e < \in g - i c e b a t h a t$ 0^(@)C $. T h e \to t a l s u r f a c e a r e a \in c o n t a c t w i t h w a t e r i s$ 0.05m^(2) $. A w h e e l i s c l a m p e d \in s t h e w a t e r and i s c o u p \leq \to a b l o c k o f m a s s M a s s h o w m \in t h e f i g u r e . A s t h e g o e s d o w n, t h e w h e e l r o t a t e s . I t i s f o u n d t ˆ a f t e r s o \pm e t i m e a s t e a d y s t a t e i s r e a c h e d \in w h i c h t h e b l o c k g o e s d o n w w i t h a c o n tan t s p e e d o f$ 10cm^(-1) $and t h e t e m p e r a t u r e o f t h e w a a t e r r e m a \in s c o n tan t a t$ 1.0^(@)C $. F \in d t h e m a s s M o f t h e b l o c k . A s \sum e t ˆ t h e h e a t f l o w o u t o f t h e w a t e r o n l y t h r o u g h t h e w a l l s \in c o n t a c t . T a k e$ g=10ms^(-2) .
View Solution
Question 14
On a winter day when the atmospheric temperature drops to $- 10^{\circ} C$ , ice forms on the surface of a lajke. (a) Calculate the rate of increases of thickness of the ice when 10cm of ice is already formed. (b) Calculate the total time taken in forming 10cm of ice. Assume that the temperature of the entire water reaches $0^{\circ} C$ before the ice starts forming. Density of water $= 1000 k g m^{- 3}$ , latent heat of fusion of ice $= 3.36 \times 10^{5} J k g^{- 1}$ and thermal conductivity of ice $= 1.7 W m^{- 1}$ ^(@)C^(-1) . Neglect the expension of water on freezing.View Solution
Question 15
Consider the situation of the previous problem. Assume that the temperature of the water at the botton of the lake remains contant at $4^{\circ} C$ as the ice forms on the surface (the heat required to maintain the temperature of the bottom layer may come from the bed of the lake). The depth of the lake is $1.0 m . S h o w t ˆ t h e t h i c k \neq s s o f t h e i c e f or m e d a a \in s a s t e a d y s t a t e m a m i μ m v a l u e . F \in d t h i s v a l u e . T h e t h e r m a l c o n d u c t i v i t y o f w a t e r$ =0.50Wm ^(-1) $^(\circ) C^{- 1}$ . Take other relevent data form the previous problelm.View Solution
Question 16
Three rods of lengths 20cm eac h and area of cross section $1 c m^{2}$ are joined to from a triangle ABC. The conductivites of the rods are $k_{A B} = 50 J s^{- 1} m^{- 1}$ (@)C^(-1) $,$ k_(BC)=200Js^(-1)m^(-1) $(\circ) C^{- 1}$ , and $k_{A C} = 400 J s^{- 1} m^{- 1}$ (@)C^(-1) $. T h e j u n c t i o n A, B and C a r e m a \int a \in e d a t$ 40^(@)C $,$ 80^(@)C $and$ 80^(@)C respectivelt. Find the rate of heat flowing through the rods AB, AC and BC . View Solution
Question 17
A semicircular rods is joined at its end to a straight rod of the same material and the same cross-sectional area. The straight rod formss a diameter of the other rod. The junction are maintaine dat different temperature. Find the ratio of the heat transffered through a cross section of the straigh rod in a given time. View Solution
Question 18
A metal rod of cross sectional area $1.0 c m^{2}$ is being heated at one end. At one time , the temperature gradient is ${5.0}^{\circ} C c m^{- 1}$ at cross section A and is ${2.5}^{\circ} C c m^{- 1}$ at cross section B. calculate the rate at which the temperature is increasing in the part AB of the rod. The heat capacity of the part AB $= 0.40 J^{\circ} C^{- 1}$ , thermal conductivity of the material of the rod. $K = 200 W m^{- 1} C^{- 1}$ . Neglect any loss of heat to the atmosphere.View Solution
Question 19
Steam at 120^(@)C $i s c o n t \in u o u s l y p a s s e d t h r o u g h a$ 50-cm $l o n g r u e r t u b e o f \in \neq r and o u t e r r a t i i$ 1.0cm $and$ 1.2cm $. T h e r \infty m t e m p e r a t u r e i s$ 30^(@)C $. C a l c a - - t e t h e r a t e o f h e a t f l o w t h r o u g h t h e w a l l s o f t h e t u b e . T h e r m a l c o n d u c t i v i t y o f r u e r$ = 0.15Js^(-1)m^(-1) $(\circ) C^{- 1}$ .View Solution
Question 20
A hole of radius $r_{1}$ is made centrally in a uniform circular disc of thickness d and radius $r_{2}$ . The inner surface (a cylinder of length d and radius $r_{1}$ is maintained at a temperature $θ_{1}$ and the oouter surface (a cylinder of length d and radius $r_{2}$ . The is maintianed at a temperature $θ_{2} (θ_{1} > θ_{2})$ .The thermal conductivity of the material of the dics is K. Calculate the heat flowing per unit time through the disc.View Solution
Question 21
A hollow tube has a length l, inner radius $R_{1}$ and outer radius $R_{2}$ . The material has a thermal conductivity K. Find the heat flowing through the walls of the tube if (a) the flat ends are maintained at temperature $T_{1}$ and $T_{2}$ (T_(2)gtT_(1) $(b) t h e \in s o f t h e t u b e i s m a \int a \in e d a t t e m p e r a t u r e$ T_(1) $and t h e o u t s i s m a \int a \in e d a t$ T_(2) .View Solution
Question 22
A composite slab is prepared by pasting two plates of thickness $L_{1}$ and $L_{2}$ and thermal conductivites $K_{1}$ and $K_{2}$ . The slab have equal cross-sectional area. Find the equivalent conductivity of the composite slab. View Solution
Question 23
Figure shows a copper rod joined to a steel rod. The rods have equal length and and the equal cross sectional area. The free end of the copper rod is kept at $0^{\circ} C$ and that of the steel rod is kept at $100^{\circ} C$ . Find the temperature at the junction of the rods. conductivity of copper $= 390 W M^{- 1}$ ^(@)C^(-1) $and t ˆ o f s t e e l$ =46Wm^(-1) $(\circ) C^{- 1}$ .
View Solution
Question 24
An aluminium rod and a copper rod of equal length $1.0 m$ and cross-sectional area. $1 c m^{2}$ are welded together as shown in figure. One end is kept at a temperature of $20^{\circ} C$ and the other at $60^{\circ} C$ Calculate the amount of heat taken out per second from the hot end. thermal conuctivity of aluminium $= 200 W m^{- 1}$ ^(@)C^(-1) $and o f c o p p e r$ =390Wm^(-1) $^(\circ) C^{- 1}$ .
View Solution
Question 25
Figure shows an aluminium rod joined to a copper rod. Each of the rods has a length of 20cm and area of ccross section $0.20 c m^{2}$ . The junction is maintained at a constant temperature $40^{\circ} C$ and the two ends are maintained at 80^(@)C $. C a l c a - - t e t h e a m o u n t o f h e a t t a k e n o u t o m t h e c o l d j u n c t i o n \in o \neq min u t e a f t e r t h e s t e a d y s t a t e i s r e a c h e d . T h e c o n d u c t i v i t i e s a r e$ K_(Al)=200Wm^(-1) $^(\circ) C^{- 1}$ . and $K_{C u} = 400 W m^{- 1}$ ^(@)C^(-1) .
View Solution
Question 26
Conside the situation shown in figure. The frame is made of the same material and has a unifrom cross-section area everywhere. Calculate the amount of heat flowing per second through a cross section of the bent part if the total heat taken out per second from the end at $100^{\circ} C$ is $130 J$ .
View Solution
Question 27
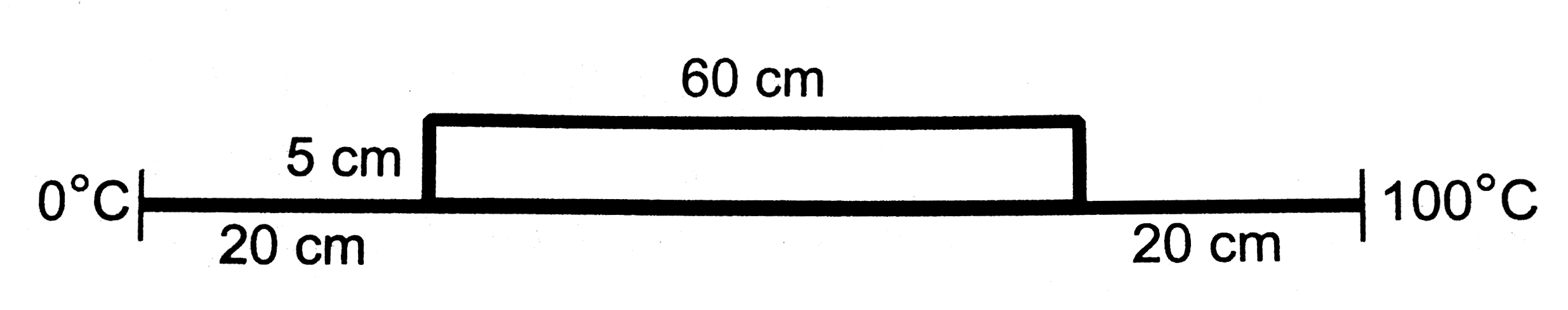Suppose the bent part of the frame of the previous problem has a thermal conductivity of $780 s^{- 1} m^{- 1}$ ^(@)C^(-1) $w h e r e a s i t i s$ 390Js^(-1)m^(-1) $^(\circ) C^{- 1}$ for the staight the bent part to the rate of heat flow through the staight part.View Solution
Question 28
A room has s window fitted with a single $0.1 m \times 2.0 m$ glass of thickness 2mm. (a) Calculate the rate of heat flow through the clossed window when the temperature inside the room is 32^(@)C $and t ˆ o u t s i s$ 40^(@)C $. (b) T h e g l a s s i s n o w r e p l a c e d b y t w o g l a s s p a n c e, e a c h h a v \in g a t h i c k \neq s s o f 1 m m and s e p a r a t e d b y a d i s tan c e o f 1 m m . C a l c a - - < e t h e r a t e o f h e a t f l o w u n d e r t h e s a m e c o n d i t i o n o f t e m p e r a t u r e . T h e r m a l c o n d u c t i v i t y o f w \in d o w g l a s s$ =1.0Js^(-1)m^(-1) $^(\circ) C^{- 1}$ and that of air $= 0.025 J s^{- 1} m^{- 1}$ ^(@)C^(-1) .View Solution
Question 29
The two rods show in figure have identical geomerical dimension.. They are in contact with two heat baths at temperature $100^{\circ} C$ . And $0^{\circ} C$ . The temperature of the junction is 70^(@)C . Find the temperature of the junction if the rods are interchanged.
View Solution
Question 30
The three rods shown in figure have identical geometrical dimensions. Heat flows from the hot end at a rate of 40W in the arrangement (a). Find the rates of heat flow when the rods are joined as in arrangement (b) and in (c). Thermal conductivities of aluminium and copper are $200 W m^{- 1}$ ^(@)C^(-1) $and$ 00Wm^(-1) $^(\circ) C^{- 1}$ respectively.
View Solution
Question 31
Four identical rods AB, CD, CF and DE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature $T_{1}$ , $T_{2}$ and $T_{3}$ respectively. Assuming no loss of heat to the atmospere, find the temperature at B.
View Solution
Question 32
Seven rods A, B, C, D, E, F and G are joined as shown in figure. All the rods have equal cross-sectional area A and length l. The thermal conductivies of the rods are $K_{A} = K_{C} = K_{0},$ K_(B)=K_(D)=2K_(0), $K_{E} = 3 K_{0},$ K_(F)=4K_(0) $and$ K_(G)=5K_(0) $. T h e r o d E i s k e p t a t a c o n s tan t t e m p e r a t u r e$ T_(1) $and t h e r o d G i s k e p t a t a c o n s tan t t e m p e r a t u r e$ T_(2)(T_(2)gtT_(1)) $. (a) S h o w t ˆ t h e r o d F h a s a u n if or m t e m p e r a t u r e$ T=(T_(1)+2T_(2))//3 $. (b) F \in d t h e r a t e o f h e a t f l o w \in g o m t h e s o u r c e w h i c h m a \int a \in s t h e t e m p e a t u r e$ T_(2) .
View Solution
Question 33
Find the rate of heat flow through a cross section of the rod shown in figure $(θ_{2} > θ_{1}$ . Thermal conductivity of the material of the rod is K.
View Solution
Question 34
A rod of negligible heat capacity has length 20cm, area of cross section $1.0 c m^{2}$ and thermal conductivity $200 W m^{- 1}$ ^(@)C^(-1) $. T h e t e m p e r a t u r e o f o \neq e n d i s m a \int a \in e d a t$ 0^(@)C $and t ˆ o f t h e o t h e r e n d i s s h o w l y and l \in e a r l y v a r i e d o m$ 0^(@)C $\to$ 60^(@)C in 10 minutes. Assuming no loss of heat through the sides, find the total heat transmitted through the rod in these 10 minutes.View Solution
Question 35
A hollow metallic sphere of radius 20cm surrounds a concentric metallic sphere of radius 5cm. The space between the two sphere is filled with a nonmetallic material. The inner and outer sphere are maintained at $50^{\circ} C$ and $10^{\circ} C$ respectively and it is found that 100J of heat passes from the inner sphere to the outer sphere per second. Find the thermal conductivity of the material between the sphere.View Solution
Question 36
Figure shown two adiabatic vessels, each containing a mass m of water at different temperature. The ends of a metal rod of length L, area of cross section. A and thermal conductivity K, are inserted in the water as shown in the figure. Find the time taken for the difference between the temperature in the vessels to become half of the original value. The specific heat capacity of water is s. Neglect the heat capacity of the rod and the container and any loss of heat top the atmosphere.
View Solution
Question 37
Two bodies of masses $m_{1}$ and $m_{2}$ and specific heat capacities $S_{1}$ and $S_{2}$ are connected by a rod of length l, cross-ssection area A, thermal conductivity K and negligible heat capacity. The whole system is thermally insulated. At time $t = 0$ , the temperature of the fisrt body is $T_{1}$ and the temperature of the second body is $T_{2} (T_{2} > T_{1})$ . Find the temperature difference between the two bodies at time t. View Solution
Question 38
An amount n (in moles) of a monatomic gas at initial temperature $T_{0}$ is enclosed in a cylinderical vessel fitted with a ligth piston. The surrounding air has a temperature $T_{s} (> T_{0})$ . And the atmospheric pressure is $P_{a}$ . Heat may be conducted between the surrounding and the gas through the bottom of the cylinder. The bottom has a surface area A, thickness x and thermal conductivity K. Assuming all change to be slow, find the distance moved by the piston in time t. View Solution
Question 39
Assume that the total surface area of a human body is $1 - 6 m^{2}$ and that it radiates like an ideal radiator. Calculate the amount of energy radiates per second by the body if the body temperature is $37^{\circ} C$ . Stefan constant $σ$ is $6.0 \times 10^{- s} W m^{- 2} K^{- 4}$ .View Solution
Question 40
Calculate the amount of heat radiated per second by a body of surface area $12 c m^{2}$ kept in thermal equilibrium in a room at temperature $20^{\circ} C$ The emissivity of the surface $= 0.80$ and $σ = 6.0 \times 10^{- s} W m^{- 2} K^{- 4}$ .View Solution
Question 41
A solid aluminium sphere and a solid copper sphere of twice the radius are heated to the same temperature and are allowed to cool under identical surrounding temperatures. Assume that the emissivity of both the spheres is the same. Find ratio of (a) the rate of heat loss from the aluminium sphere to the rate of all of temperature of the copper sphere. The specific heat capacity of aluminium $= 900 J k g^{- 1}$ ^(@)C^(-1) $. and t ˆ o f c o p p e r =$ 390Jkg^(-1) $^(\circ) C^{- 1}$ . The density of copper =3.4 times the correct wattage.View Solution
Question 42
A 100W bulb has tungsten filament of total length $1.0 m$ and radius $4 \times 10^{- 5} m$ . The emissivity of the filament is $0.8$ and $σ = 6.0 \times 10^{- 8} W m^{- 2} K^{- 4}$ . Calculate the temperature of the filament when the bulb is operating at correct wattage.View Solution
Question 43
A spherical ball of surface area $20 c m^{\circ}$ absorbs any radiation that falls on it. It is suspended in a closed box maintained at $57^{\circ} C$ . (a) Find the amount of radiation falling on the ball per second. (b0 Find the net rate of heat flow to or from the ball at an instant when its temperature is $200^{\circ} C$ . Stefan constant $= 6.0 \times 10^{- s} W m^{- 2} K^{- 4}$ . View Solution
Question 44
A spherical tungsten pices of radius $1.0 c m$ is suspended in an evacuated chamber maintained at $300 K . T h e π c e s i s m a \int a \in e d a t 1000 K b y h e a t \in g i t e \leq c t r i c a l l y . F \in d t h e r a t e a t w h i c h t h e e \leq c t r i c a l e \neq r g y μ s t b e \supset p l i e d . T h e e m i s s i v i t y o f t u n g s t e n i s$ 0.30 $and t h e S t e f a n c o n s tan t σ i s$ 6.0xx10^(-s)Wm^(-2)K^(-4) . View Solution
Question 45
A cubical block of mass $1.0 k g$ and edge $5.0 c m$ is heated to $227^{\circ} C$ . It is kept in an evacuated chamber maintained at $27^{\circ} C$ . Assuming that the block emits radiation like a blackbody, find the rate at which the temperature of the block will decreases. Specific heat capacity of the material of the block is $400 J k g^{- 1} K^{- 1}$ .View Solution
Question 46
A copper sphere is suspended in an evacuated chamber maintained at 300K. The sphere is maintained at a constant temperature of 500K by heating it electrically. A total of 210W is electric power is needed to do it. When the surface of the copper sphere is completely blanked, 700W is needed to maintain the same temperature of the sphere. Calculate the emissivity of copper.View Solution
Question 47
A spherical ball A of surface area $20 c m^{2}$ is kept at the centre of a hollow spherical shell B of area $80 c m^{2}$ . The surface of A and the inner surface of B emit as blackbodies. Both A and B are at 300K. (a) How much is the radiation energy emitted per second by the ball A? (b) How much is the radiation energy emitted per second in the inner surface of B? (c) How much of the energy emitted by the inner surface of B falls back on this surface itself?View Solution
Question 48
A cylinderical rod of length 50cm and cross sectional area $1 c m^{2}$ is fitted between a large ice chamber at $0^{\circ} C$ and an evacuated chamber maintained at $27^{\circ} C$ as shown in figure. Only small protions of the rod are insid ethe chamber and the rest is thermally insulated from the surrounding. The cross section going inti the evacuted chamber is blackened so that it completely absorbe any radiation falling on it. The temperatuere of the blackened end is $17^{\circ} C$ when steady state is reachhed. Stefan constant $σ = 6 \times 10^{- s} W m^{- 2} K^{- 4}$ . Find the thermal conductivity of the material of the rod.
View Solution
Question 49
One end of a rod length 20cm is inserted in a furnace at 800K. The sides of the rod are coved with an insulating material and the other end emits radiation like a blackbody. The temperature of this end is 750K in the steady state. The temperature of the surrounding air is 300K. Assuming radiation to be the only important mode of energy tranfer between the surrounding and the open end of the rod, find the thermal conductivity of the rod. Stefan constant $σ s = 6.0 \times 10^{- 1} W m^{- 2} K^{- 4}$ .View Solution
Question 50
A calorimeter of negligible heat capacity contains 100cc of water at $40^{\circ} C$ . The water cools to $35^{\circ} C$ in 5minutes. The water is now replaced by k-oil of equal volume at $40^{\circ} C$ . Find the time taken for the temperature to become $35^{\circ} C$ under similar conditions. Specific heat cpacities of water and K-oil are $4200 J k g^{- 1} K^{- 1}$ and $2100 J k g^{- 1} K^{- 1}$ respectively. Density of K-oil $= 800 k g m^{- 3}$ .View Solution
Question 51
A body cools down from $50^{\circ} C$ to $45^{\circ} C$ in 5 minutes and to $40^{\circ} C$ in another 8 minutes. Find the temperature of the surrounding. View Solution
Question 52
A calorimeter containes 50g of water at $50^{\circ} C$ . The temperature falls to $45^{\circ} C$ in 10 minutes. When the calorimeter contains 100g of water at $50^{\circ} C$ it takes 18 minutes for the temperature to become $45^{\circ} C$ . Find the water equivalent of the calorimeter.View Solution
Question 53
A metal ball of mass 1kg is heated by means of a 20W heater in a room at $20^{\circ} C$ . The temperature of the ball becomes steady at $50^{\circ} C$ . (a) Find the area of loss of heat to the surrounding when the ball is at $- 50^{\circ} C$ . (b) Assuming Newton's law of cooling, calculate the rate of loss of heat to the surrounding when the ball is at $30^{\circ} C$ . (c) Assume that the temperature of the ball rises uniformly from $20^{\circ} C$ to $30^{\circ} C$ in 5 minutes. Find the total loss of heat to the surrounding during this period. (d) Calculate the speific heat capicity of the metal.View Solution
Question 54
A metal block of heat capacity $90 J / .^{\circ} C$ placed in a room at $25^{\circ} C$ is heated electrically. The heater is switched off when the temperature reaches $35^{\circ} C$ . The temperature of the block rises at the rate of $2^{\circ} C / s$ just after the heater is switched on and falls at the rate of ${0.2}^{\circ} C / s$ just after the heater is switched off. Assume Newton's law of cooling to hold (a) Find the power of the heater. (b) Find the power radiated by the block just after the heater is switched off. (c ) Find the power radiated by the block when the temperature of the block is $30^{\circ} C$ . (d) Assuming that the power radiated at $30^{\circ} C$ respresents the average value in the heating process, find the time for which the heater was kept on. View Solution
Question 55
A hot body placed in a surrounding of temperature $θ_{0}$ obeys Newton's law of cooling $\frac{d θ}{d t} = - k (θ - θ_{0})$ . Its temperature at $t = 0$ is $θ_{1}$ the specific heat capacity of the body is s and its mass is m. Find (a) the maximum heat that the body can lose and (b) the time starting from $t = 0$ in which it will lose 90% of this maximum heat.View Solution

Home
Ask Doubt
Profile

EXERCIESE from HC VERMA PHYSICS (HINGLISH) HEAT TRANSFER for Class 11

All Exercises from HC VERMA PHYSICS (HINGLISH) Class 11 PHYSICS HEAT TRANSFER