Examples from CENGAGE Chapter 5 AREA for Class 12

Question 1

Question 2

Question 3

Question 4

Question 5

Question 6

Question 7

Question 8

Question 9

Question 10

Question 11

Question 12

Question 13

Question 14

Question 15

Question 16

Question 17

Question 18

Question 19

Question 20

Question 21

Question 22

Question 23

Question 24

Question 25

Question 26

Question 27

Question 28

Question 29

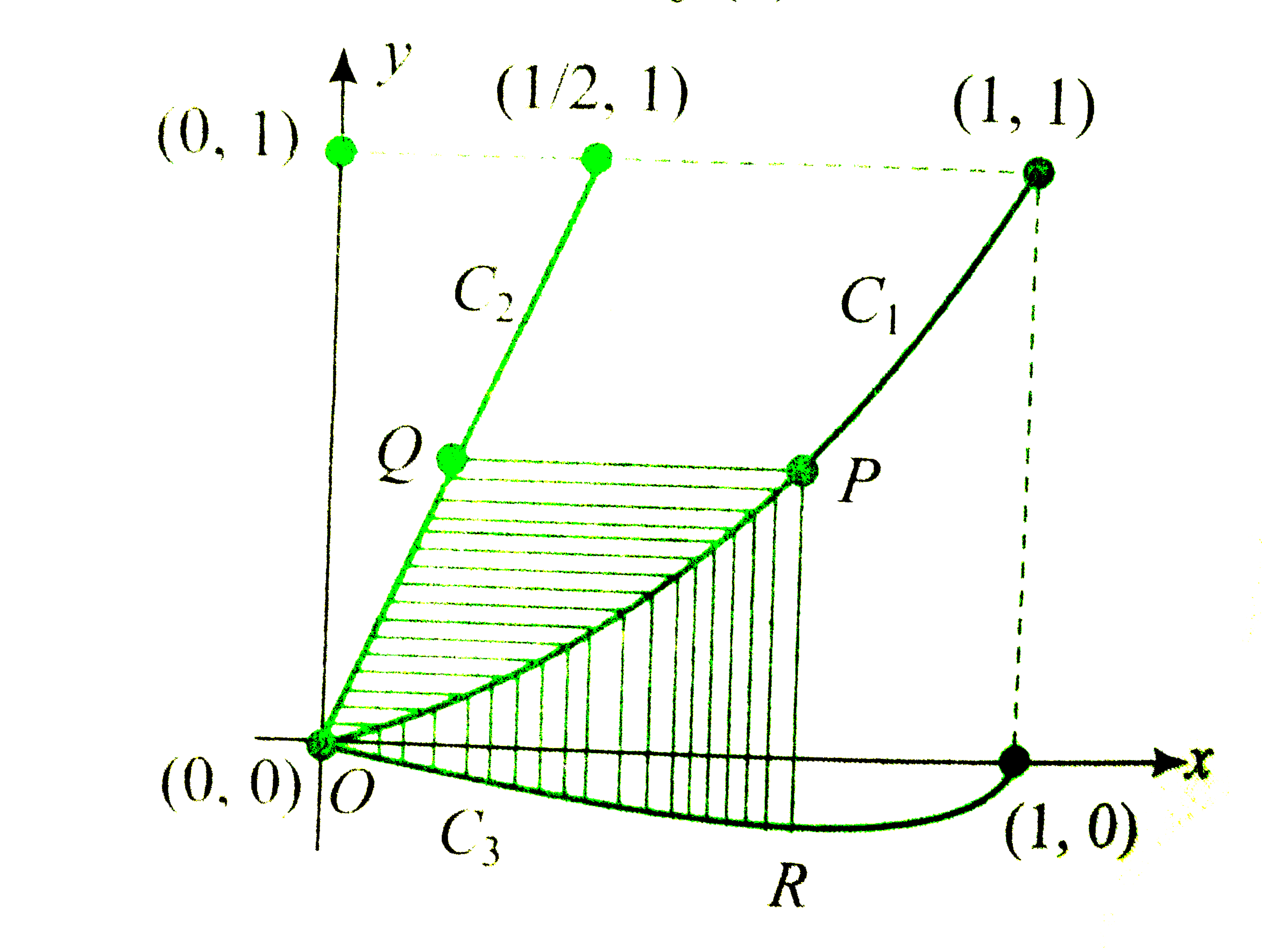
Let $C_1\text{and}{C}_2$ be the graphs of the functions $y=x^2\text{and}y=2x,$ respectively, where $0\le x\le 1.\text{Let}{C}_3$ be the graph of a function y=f(x), where $0\le x\le 1,f\left(0\right)=0.$ For a point P on $C_1,$ let the lines through P, parallel to the axes, meet $C_2\text{and}{C}_3$ at Q and R, respectively (see figure). If for every position of $P\left(on{C}_1\right),$ the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).

Question 30

Question 31

Question 32

Question 33

Question 34

Question 35

Question 36

Question 37

Question 38

Question 39

Question 40

Question 41

Question 42

Question 43

Question 44

Question 45

Question 46