Exercises from HC VERMA PHYSICS Chapter 8 ELECTROMAGNETIC INDUCTION for Class 12
| Class 12 | PHYSICS |
| Chapter | ELECTROMAGNETIC INDUCTION |
| HC VERMA PHYSICS | Exercises |
| Medium | English |
| Academic Year | 2023-2024 |
Question 3
(a) the magnetic field in a region varies as shown in . Calculate the average induced emf in a conducting loop of area 2.0X10^(-3) m^2 placed perpendicular to the field in each of the10ms intervals shown. (b) In which intervals is the emf not constant? Neglect the behaviour near the ends of 10 ms intervals.
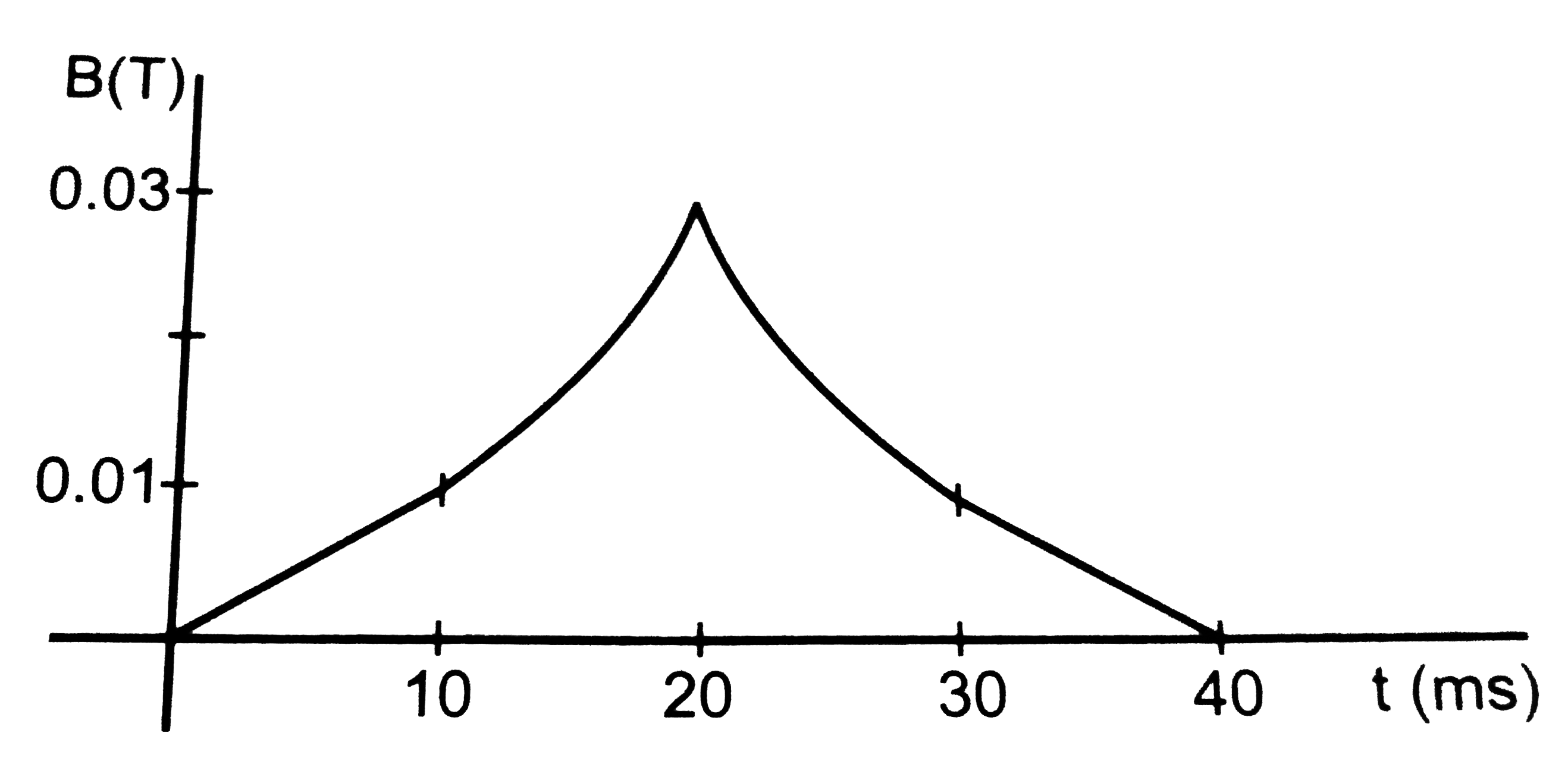 View Solution
View SolutionQuestion 6
A square- shaped copper coil has edges of length 50cm and contains 50 turns. It is placed perpendicular to 1.0 T magnetic field. It is removed form the magnetic field in 0.25 s and restored in its joriginal place in the next 0.25 s. Find the magnitude of the average emf induced in the loop during (a) its removal, (b) its restoration and (c) its motion.View SolutionQuestion 8
A conducting loop of area 5.0cm2 is placed in a magnetic field which varies sinusodially with time as B=B0sinωt where B0=0.20T and ω=300s−1. The normal to the coil makes an angle of 60∘ with the field. Find (a) the maximum emf induced in the coil, (b) the emf induced at τ=(τ900)s and (c) the emf induced at t=(π600)s.View SolutionQuestion 9
Shows a conducting square loop placed parallel to the pole faces of a ring magnet. The pole faces have an are of 1cm^2 each and the field between the poles is 0.10 T. The wires making the loop are all outside the magnetic field. If the magnet is removed in 1.0 s, what is the average emf induced in the loop?
 View Solution
View SolutionQuestion 10
A conducting square loop having edges of length2.0 cm is rotated through 180∘ about a diagonal in 0.20s. A magnetic field B exists in the region which is perpendicular to the loop in its initial position. If the average induced emf during the rotation is 20 mV, find the magnitude of the magnetic field.View SolutionQuestion 11
A conducting loop of face area A and resistance R is plaed perpendicular to a magnetic field B. The loop is withdrawn completely from the field. Find the charge which flows through any cross section of the wire in the process. Note that it is independent of the shape of the loop as well as the way it is withdrawn.View SolutionQuestion 12
A long solenoid of radius 2 cm has 100 turns/cm and carries a current of 5A. A coil of radius 1 cm having 100 turns and a total resistance of 20 Omega is placed inside the solenoid coaxially. The coil is connected to a galvanometer. If the current in the solenoid is reversed in direction, find the charge flown through the galvanometer.View SolutionQuestion 13
The north pole of a magnet is brought down along the axis of a horizontal circular coil . As a result, the flux through the coil changes from 0.35 weber to 0.85 weber in an interval of half a second. Find the average emf induced during this period. Is the induced current clockwise or anticlockwise as you look into the coil from the side of the magnet?
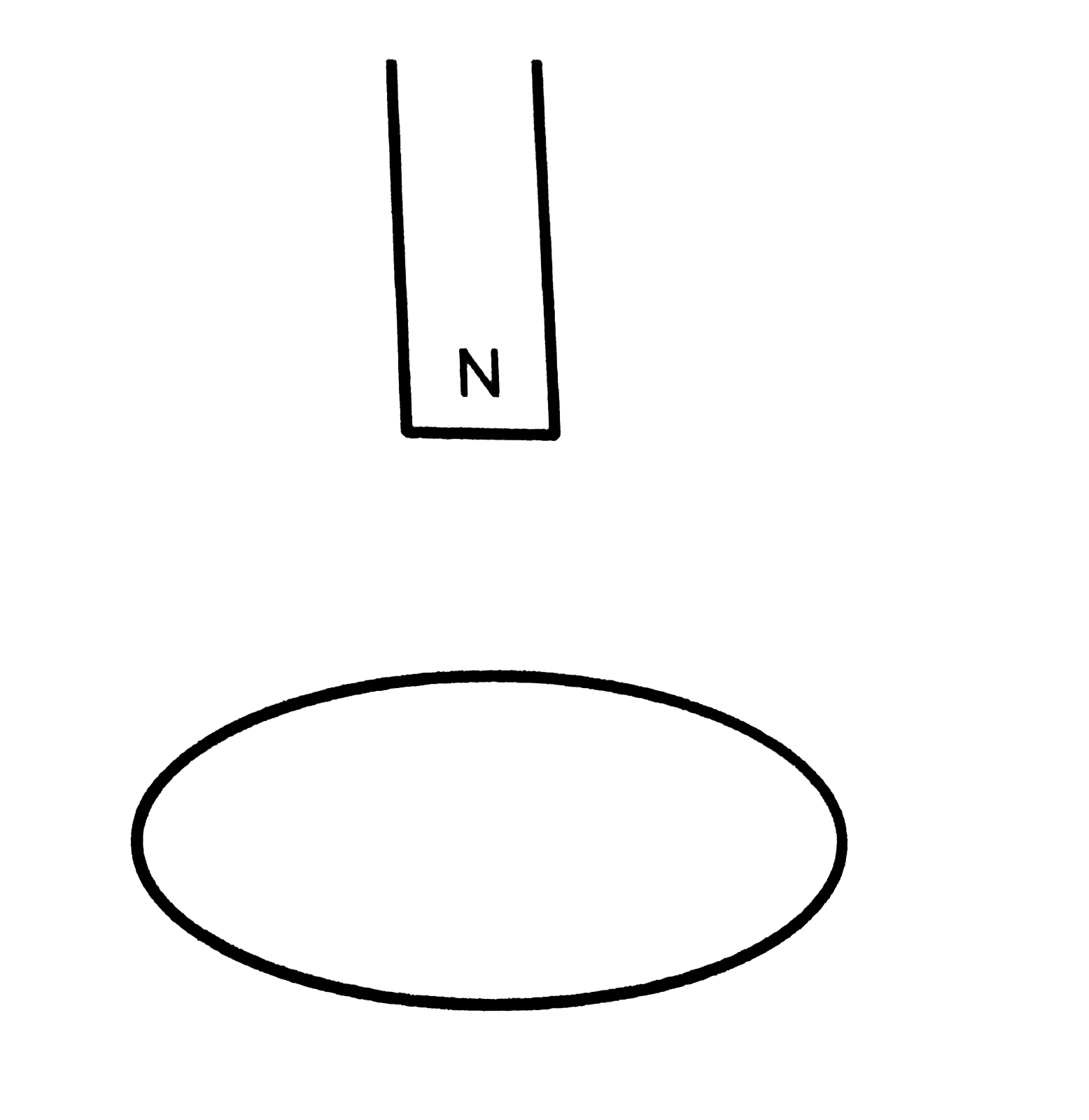 View Solution
View SolutionQuestion 16
A uniform magnetic field B exists in a cylindrical region of radius 10 cm as shown in. A uniform wire of length 80 cm and resistance 4.0 Omega is bent into a square frame and is placed with one side along a diameter of the cylindrical region. If the magnetic field increases at a constant rate of 0.010 T/s, find the current induced in the frame.
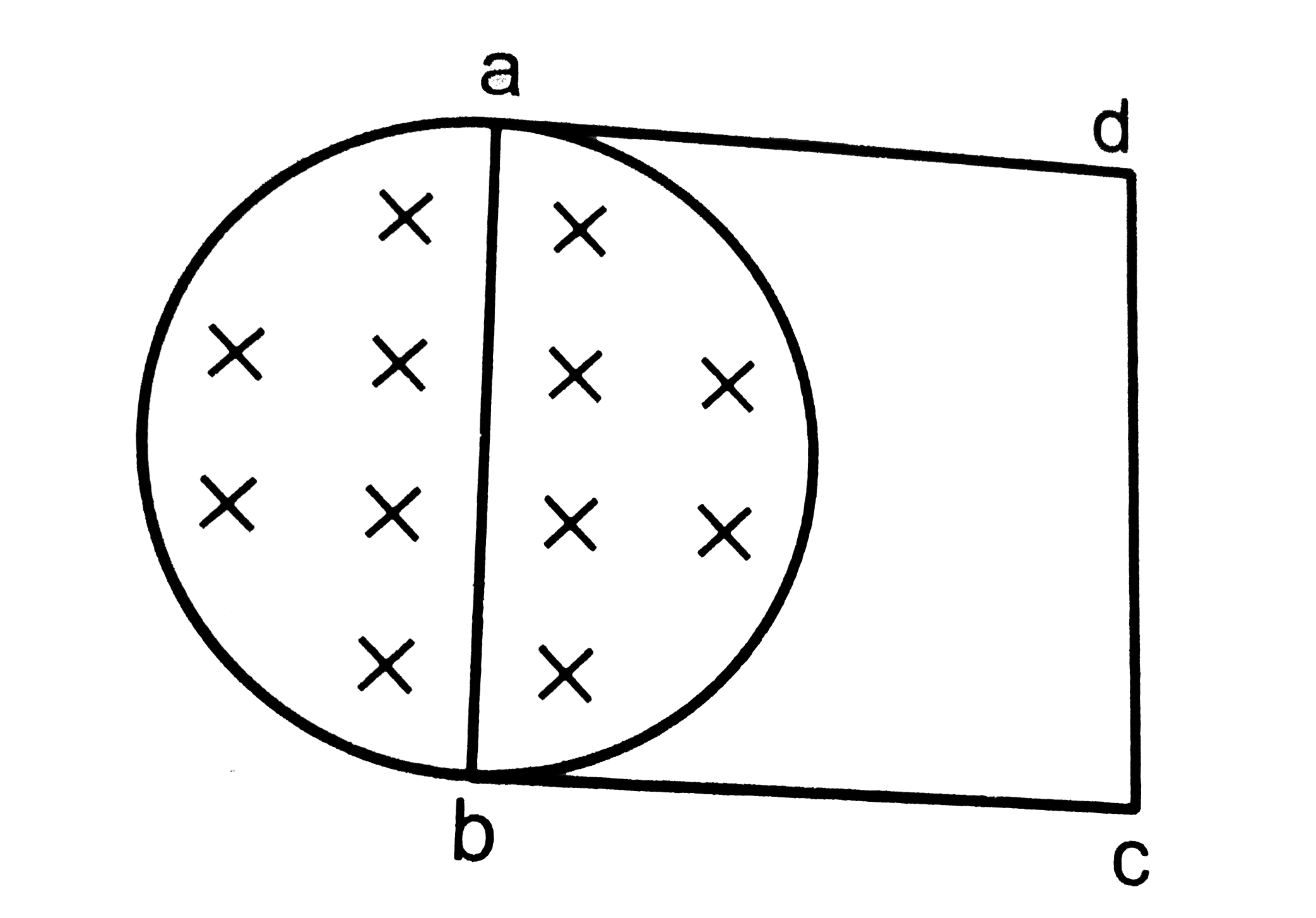 View Solution
View SolutionQuestion 17
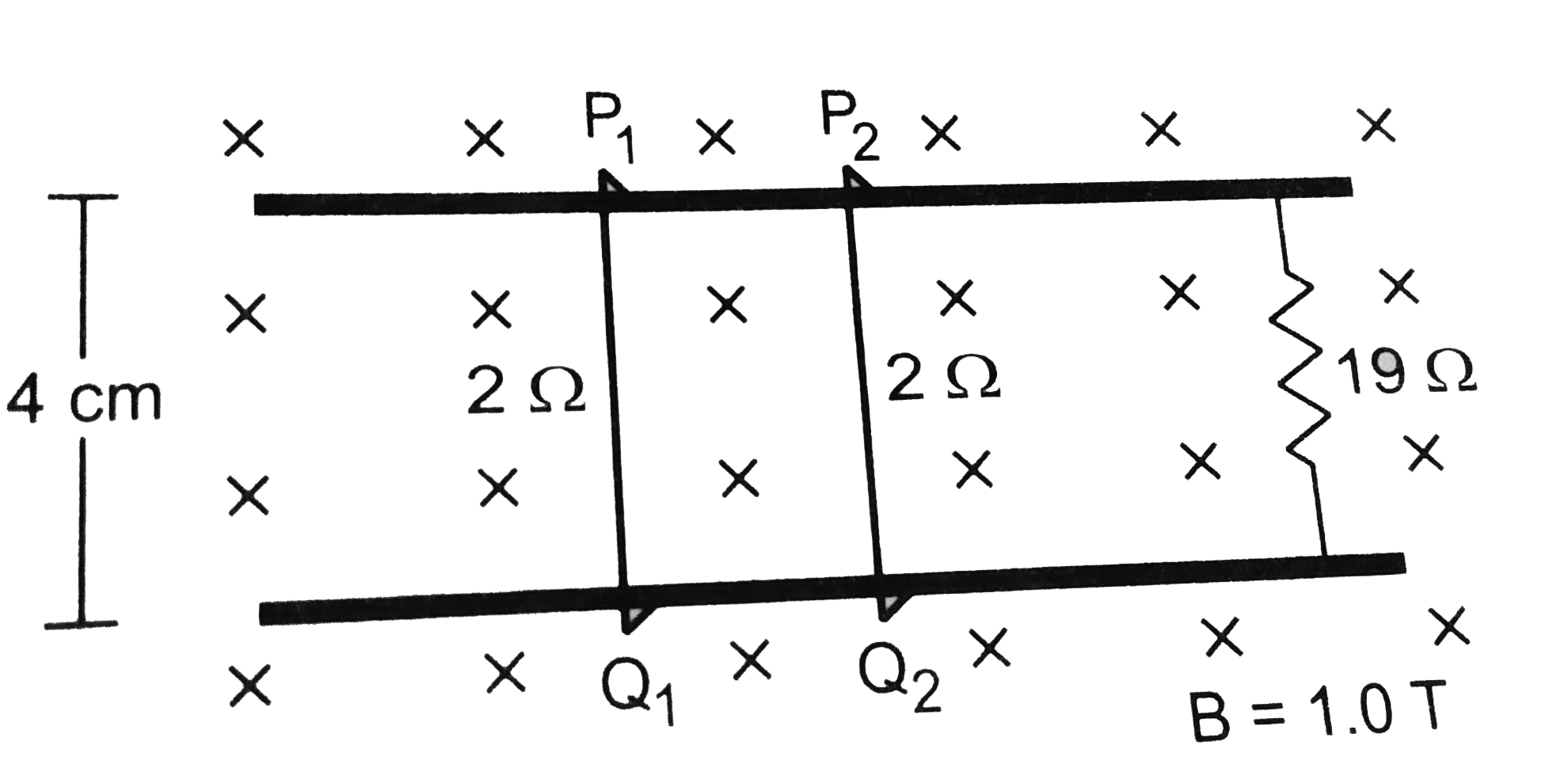
The magnetic field in the cylindrical region shown in increases at a constant rate of 20.0 mT/s. Each side of the square loop abcd and defa has a length of 1.00 cm and a resistance of 4.00Ω. Find the current (magnitude and sense) in the wire ad if (a) the switch S1) is closed but S2 is open, (b) S1 is open but S2 is closed, (c) both S1 and S2 are open and (d) both S1 and S2 are closed.
 View Solution
View SolutionQuestion 18
A circular coil of radius 2.00 cm has 50 turns. A uniform magnetic field B= 0.200 T exists in the space is a direction parallel to the axis of the loop. The coil is now rotated about a diameter through an angle of 60.0∘. The operation takes 0.100 s. (a) find the average emf induced in the coil. (b) if the coil is a closed one(with the two ends joined together) and has a resistance of 4.00Ω. calculate the net charge crossing a cross- section of the wire of the coil.View SolutionQuestion 19
A closed coil having 100 turns is rotated in a uniform magnetic field B=4.0×10−4 T about a diameter which is perpendicular to the field. The angular velocity of rotation is 300 revolutions per minute. The area of the coil is 25cm2 and its resistance is 4.0Ω. Find (a) the average emf developed in the half a turn form a position where the coil is perpendicular to the magnetic field, (b) the average emf in a full turn and (c) the net charge displaced in part (a).View SolutionQuestion 20
A coil of radius 10 cm and resistance 40Ω has 1000 turns. It is placed with its plane vertical and its axis parallel to the magnetic meridian. The coil is connected to a galvanometer and is rotated about the vertical diameter through an angle of 180∘. Find the charge which flows through the galvanometer if the horizontal component of the earth's magnetic field is BH=3.0×10−5T.View SolutionQuestion 21
shows a circular wheel of radius 10.0 cm whose upper half, shown dark in the figure, is made of iron and the lower half of wood. The two junctions are joinded by an iron rod. A uniform magnetic field B of magnitdue 2.00X 10^(-4) T exists in the space above the central line as suggested by the figure. The wheel is set into pure rolling on the horizontal surface. The wheel is set into pure rolling on the horizontal surface. If it takes 2.00 seconds for the iron part to come down and the wooden part to go up, find the average emf induced during this period.
 View Solution
View SolutionQuestion 25
The two rails of a railway track, insulated form each other and from the ground, are connected to a millivoltmeter. What will be the reading of the millivoltmeter when a train travels on the track at a speed of 180kmh−1? The vertical component of earth's magnetic field is 0.2×10−4 and the rails are separated by 1m.View SolutionQuestion 26
A right angled triangle abc, made from a metallic wire, moves at a uniform speed v in its plane as shown in . A uniform magnetic field B exists in the perpendicular direction. Find the emf induced (a) in the loop abc, (b) in the segment bc, (c ) in the segment or and (d) in the segment ab.
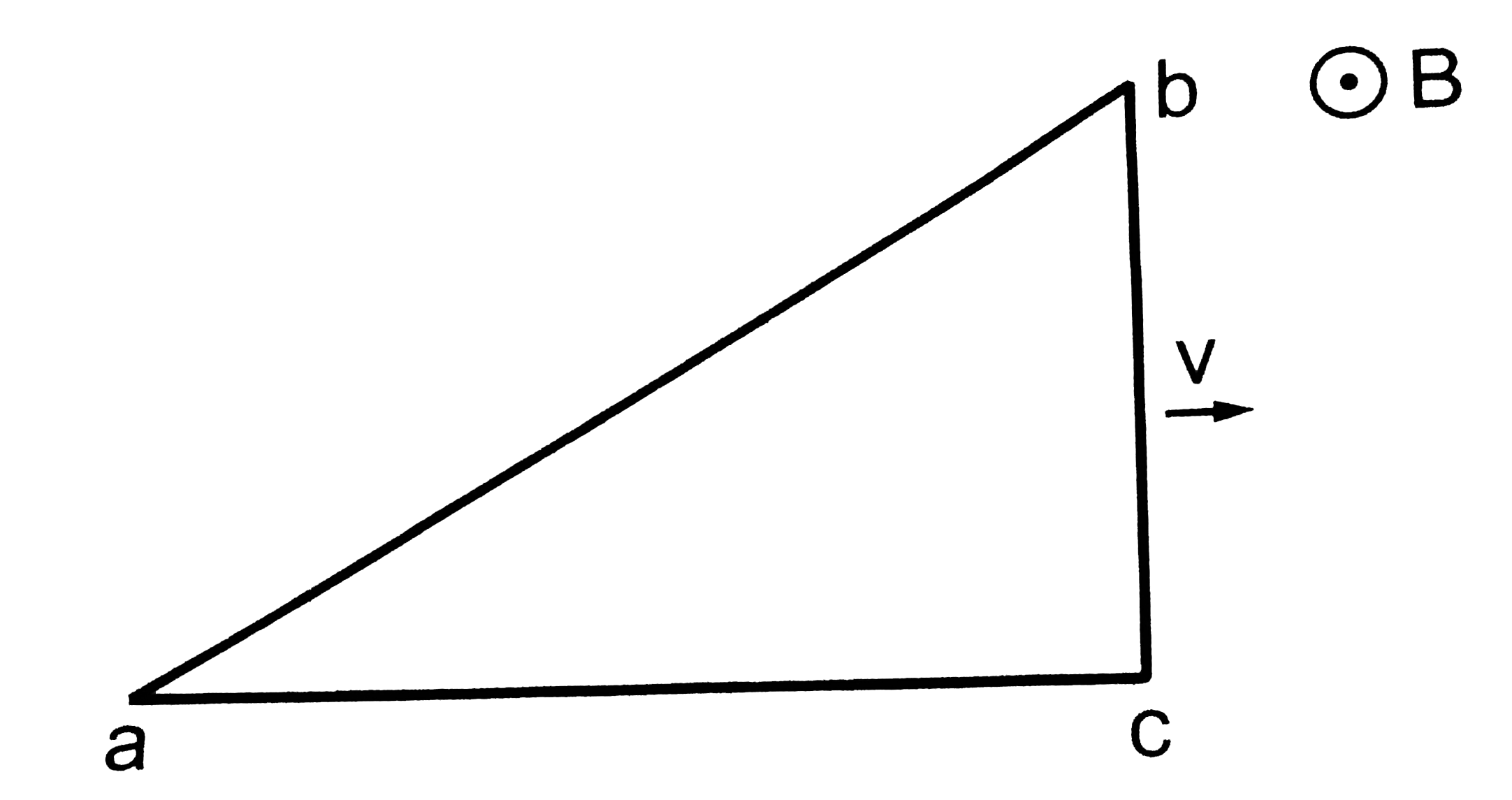 View Solution
View SolutionQuestion 27
A copper wire bent in the shape of a semicircle of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the direction perpendicular to the plane of the wire. Find the emf induced between the ends of the wire if (a) the velocity is perpendicular ot the diameter joining free ends, (b) the velocity is parallel to this diameter.View SolutionQuestion 28
A wire of length 10cm translates in a direction making an angle of 60∘ with its length. The plane of motion is perpendicular ot a uniform magnetic field of 1.0 T that exists in the space. Find the emf induced between the ends of the rod if the speed of translation of 20 cm s^(-1).View SolutionQuestion 29
A circular copper ring of radius r translates in its plane with a constant velocity v. A uniform magnetic field b exists in the space in a direction perpendicular ot the plane of the ring. Consider different pairs of diametrically opposite points on the ring. (a) Between which pair of points is the emf? (b) Between which pair of points is the emf minimum? What is the value of this minimum emf?View SolutionQuestion 31
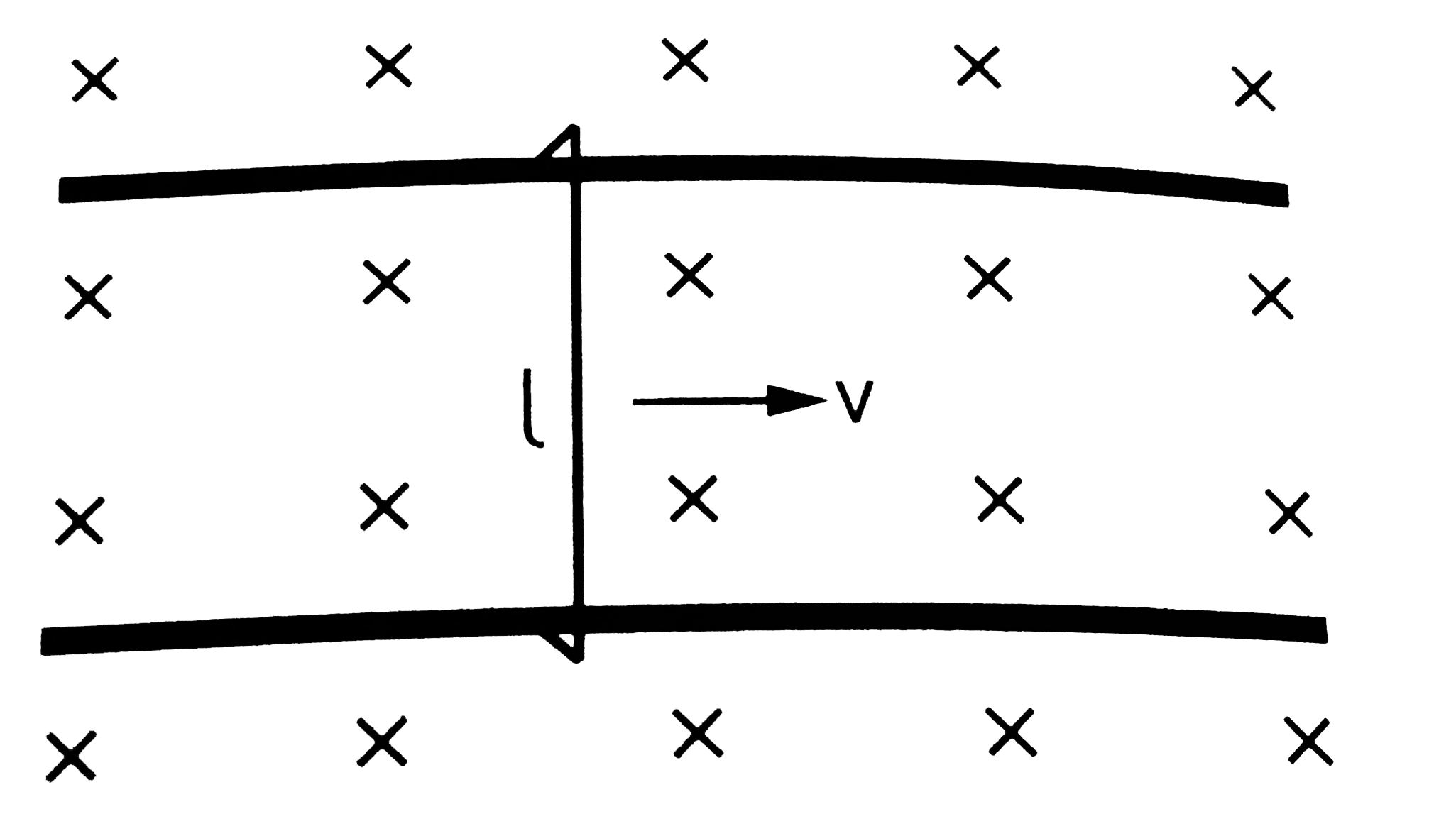
shows a long U shaped wire of width l placed in a perpendicular magnetic field B. A wire of length l is slid on the U shaped wire with a constant velocity v towards right. The resistance of all the wires is r per unit length. At t =0, the sliding wire is close to the left edge of the U shaped wire. Draw an equivalent circuit diagram, showing the induced emf as a battery. Calculate the current in the circuit.
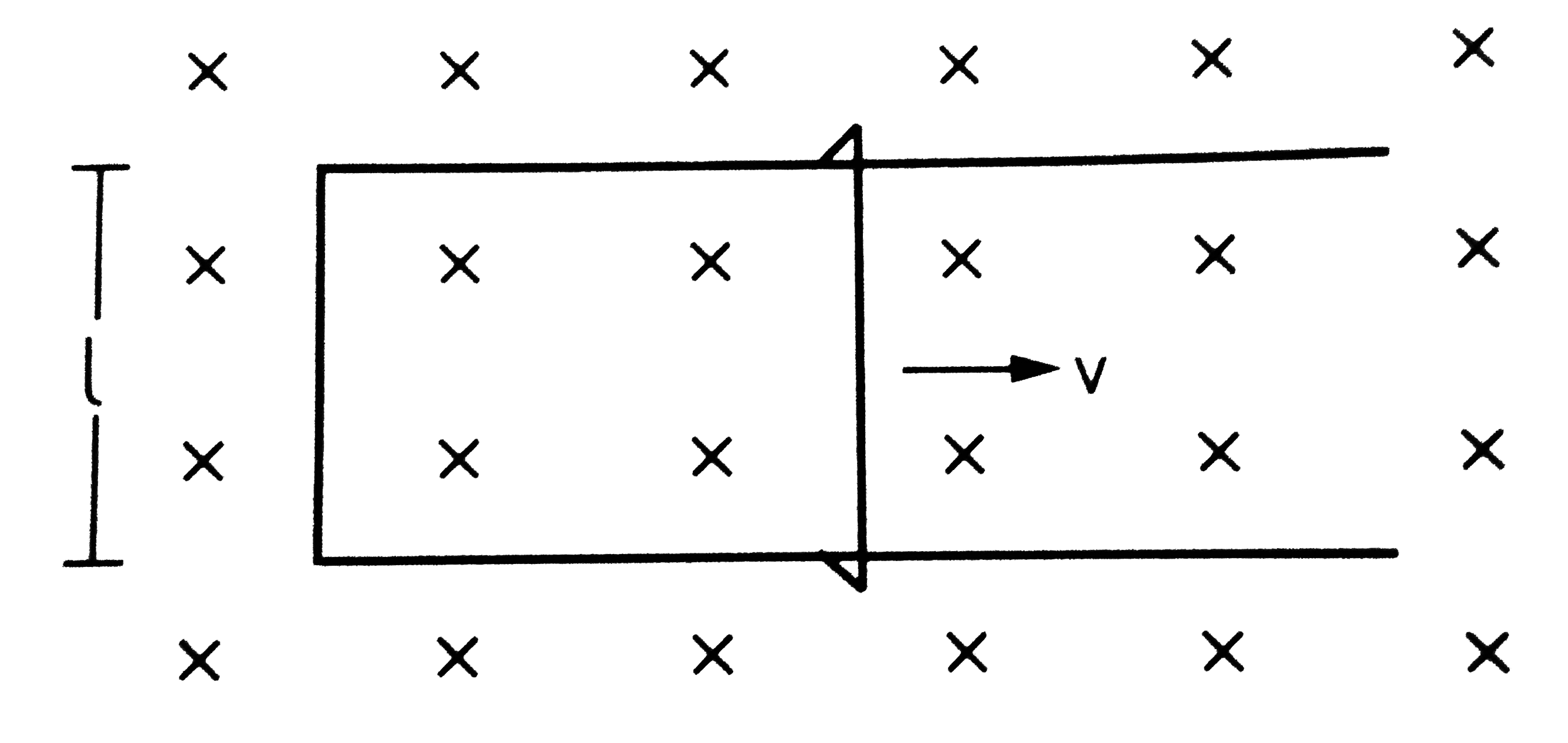 View Solution
View SolutionQuestion 33
Consider the situation shown in . The wire PQ has mass m, resistance r and can slide on the smooth, horizontal parallel rails separted by a distance l. The resistance of the rails is negligible. A uniform magnetic field B exists in the rectangualr region and a resistance R connects the rails outsided the field region At t= 0, the wire PQ is puched towards right with a speed v0. find (a) the current in the loop at an instant when the speed of the wire PQ is v, (b) the acceleration of the wire at this instatn, (c ) the velocity v as a function of x and (d) the maximum distance the wire will move.
 View Solution
View SolutionQuestion 34
A rectangular frame of wire abcd has dimensions 32cm X 8.0 cm and a total resistance of 2.0Ω. It is pulled out of a magnetic field B=0.020T by applying a force of 3.2×10−5 N . It is found that the frame moves with constant speed. Find (a) this constant speed, (b) the emf induced in the loop, (c) the potential difference between the points c and d.
 View Solution
View SolutionQuestion 35
Shows a metallic wire of resistance 0.20Ω sliding on a horizontal, U shaped metallic rail The separation between the parallel arms is 20 cm. jAn electric current of 2.0μA passes through the wire when it is slid at a rate of 20cms−1. If the horizontal component of the earth's magnetic field is 3.0X10−5 T, calculate the dip at the place.
 View Solution
View SolutionQuestion 36
A wire ab of length l, mass m and resistance R slide on a smooth, thick pair of metallic rails joined at the bottom as shown in . The plane of the the rails makes an angle θ with the horizontal. A vertical magnetic field B exists in the region. if the wire slides on the rails at a constant speed v, show that B=√mgRsinθvl2cosθ.
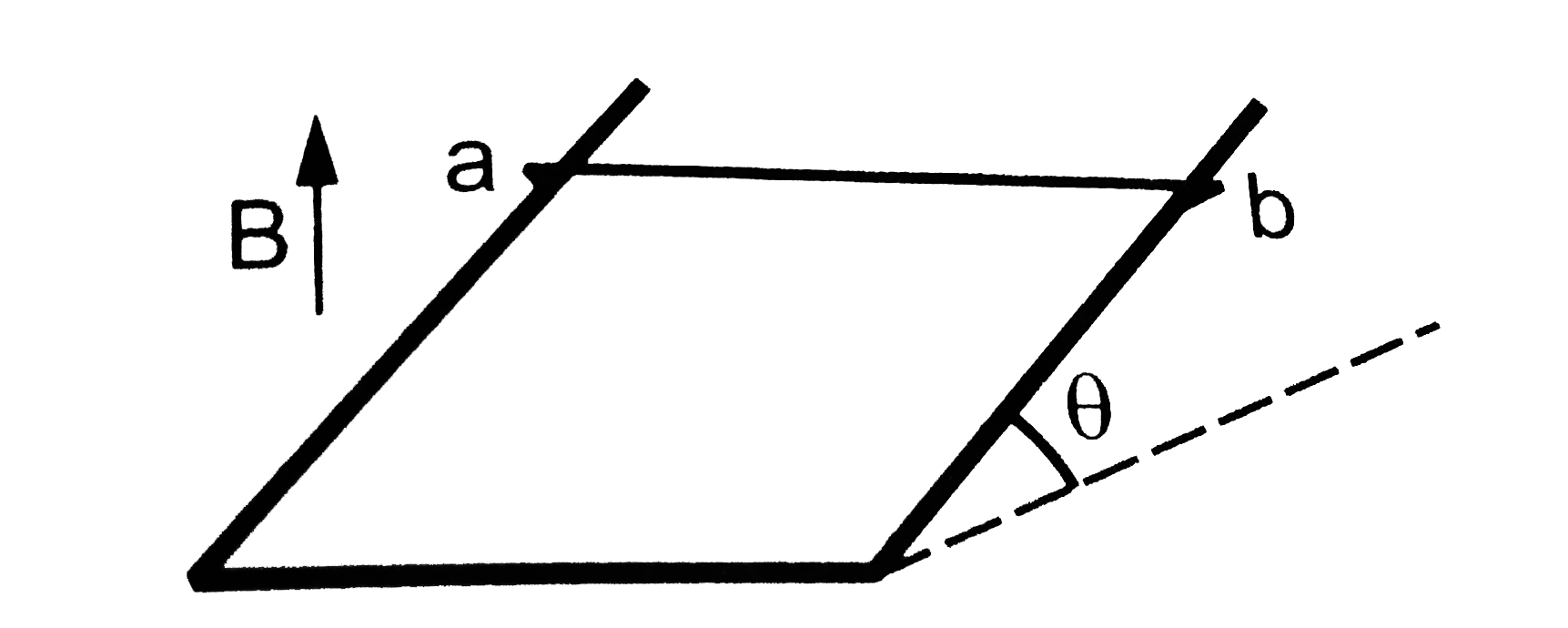 View Solution
View SolutionQuestion 41
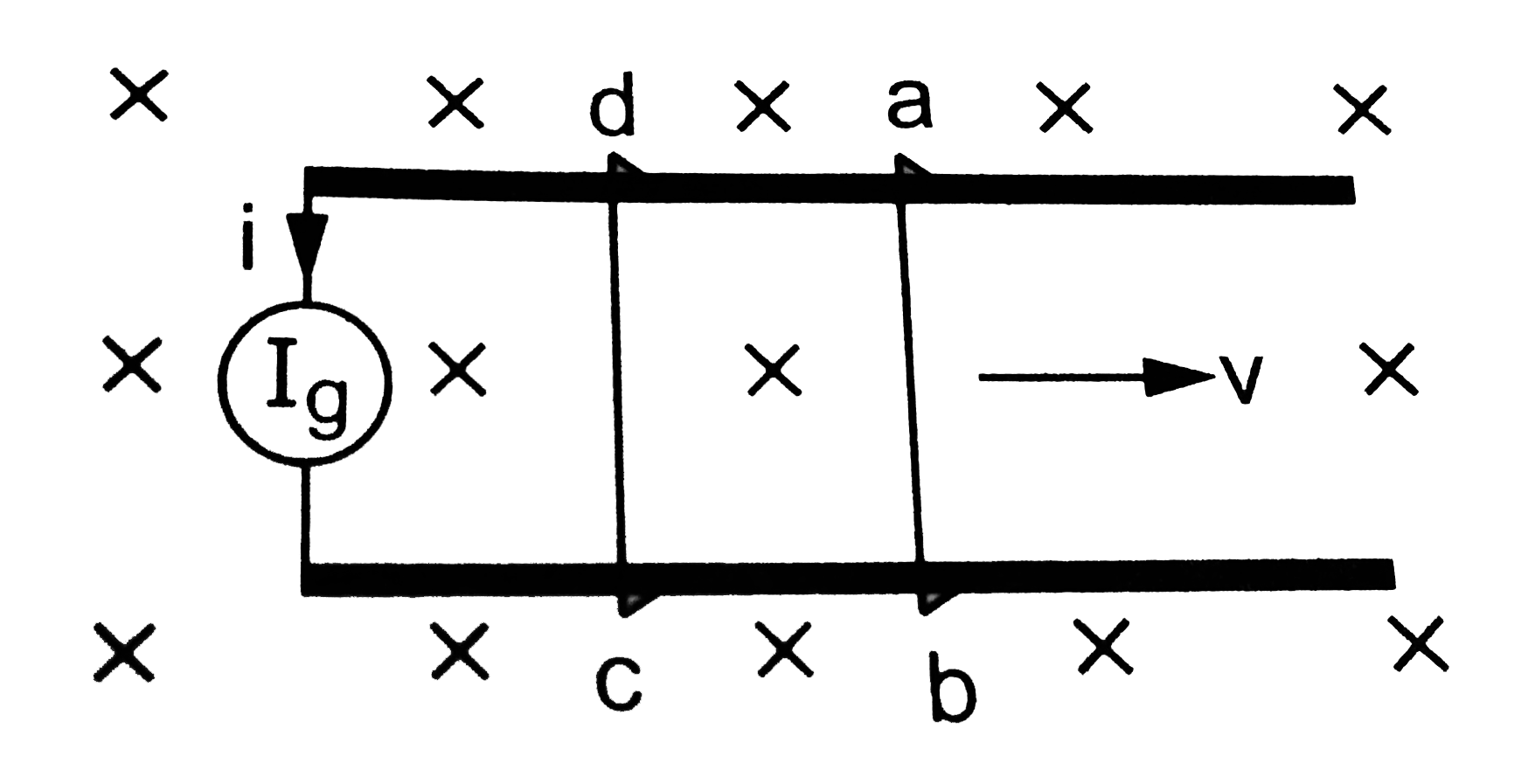
The current generator ig, shown in , sends a constant current I through the circuit. The wire ab has a length l and mass m and can slide on the smooth, horizontal rails connected to lg. The entire system lies in a vertical magnetic field B. Find velocity of the wire as a function of time.
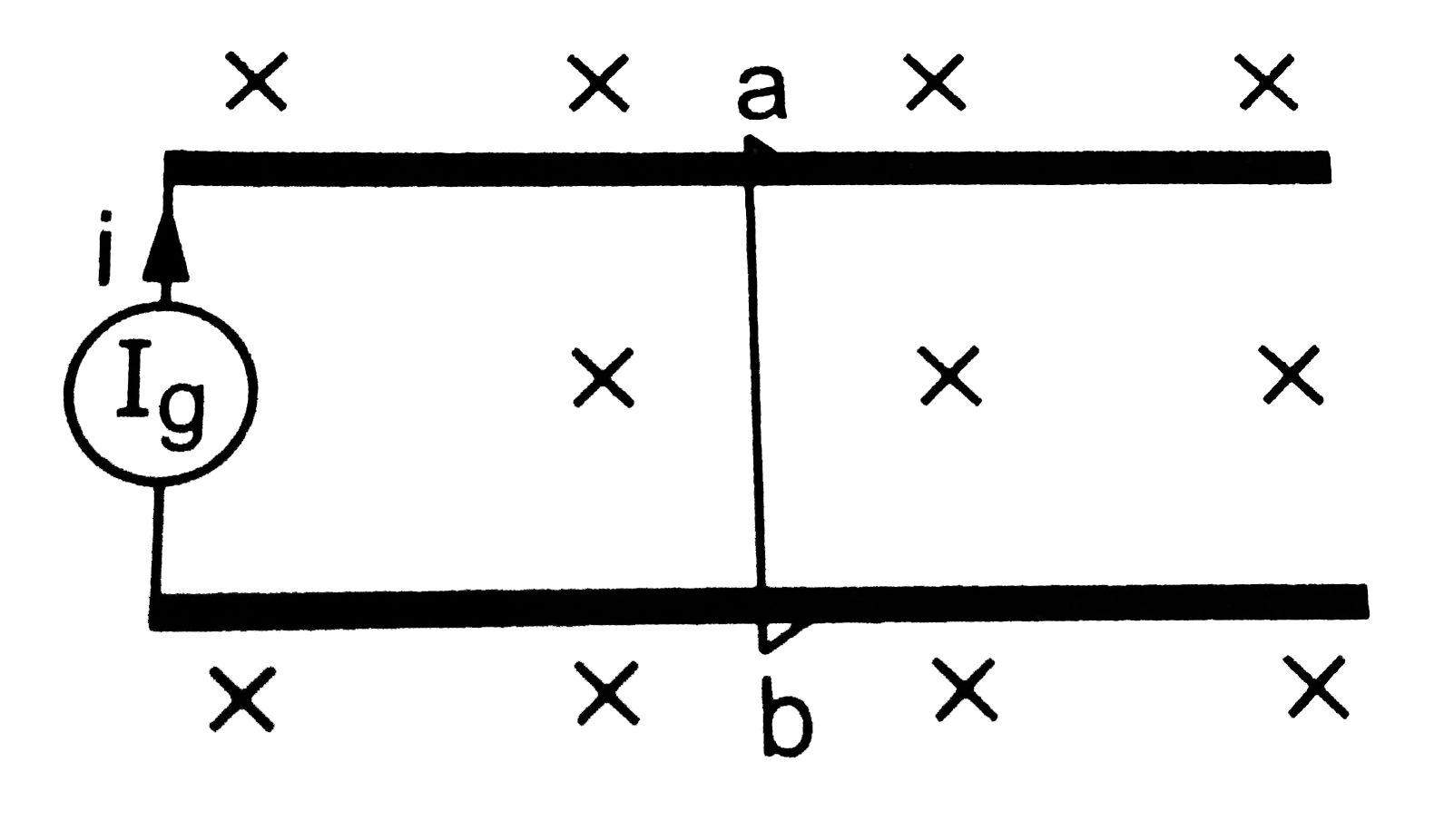 View Solution
View SolutionQuestion 42
The system containing the rails and the wire of the previous problem is kept vertically in a uniform horizontal magnetic field B that is perpendicular to the plane of the rails. It is found that the wire stays in equilibrium. If the wire ab is replaced by another of double its mass, how long will it take in falling through a distance equal ot its length?
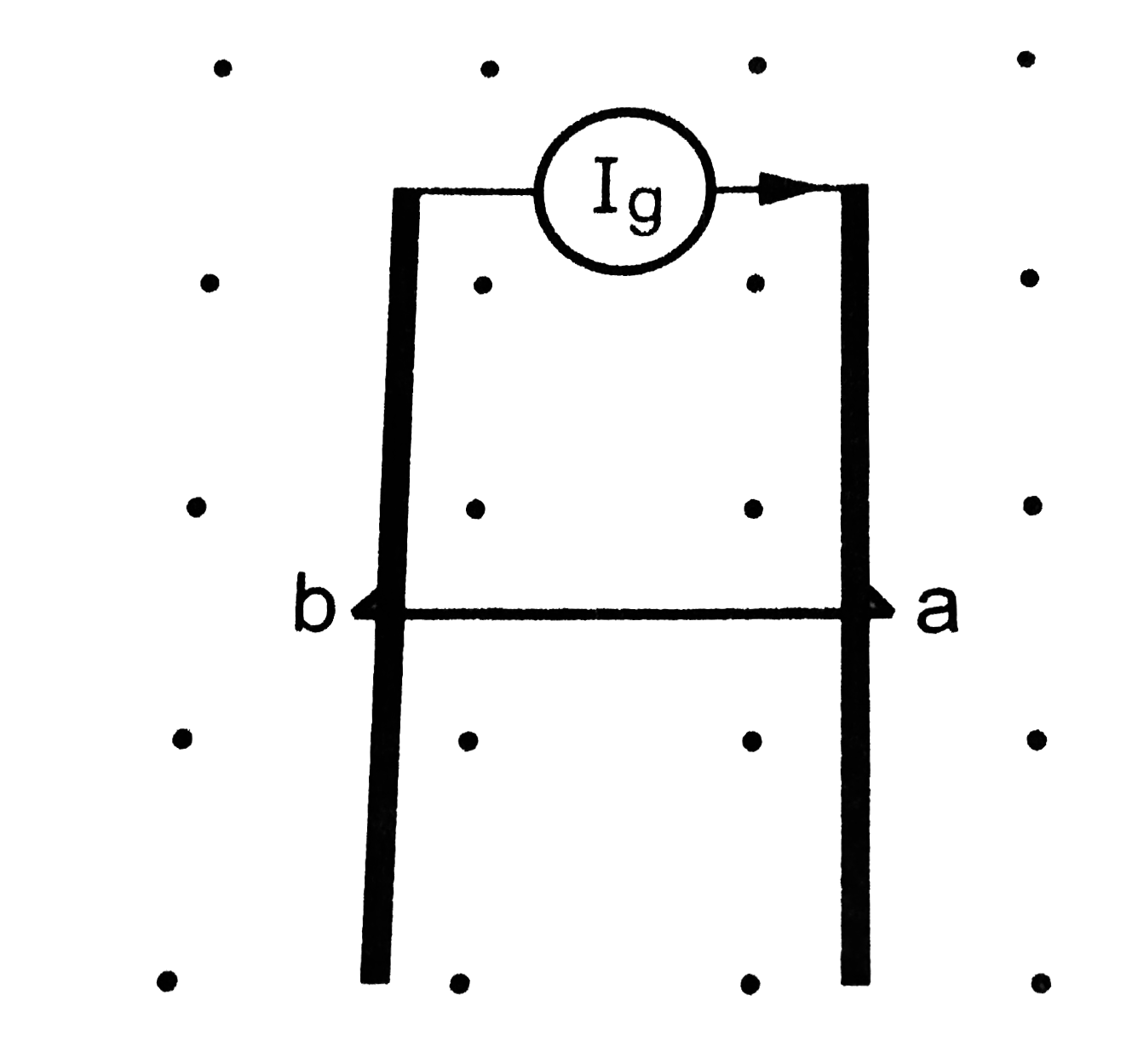 View Solution
View SolutionQuestion 43
The rectangualr wire- frame, shown in has a width d, mass m, resistance R and a large length. A uniform magnetic field B exists to the left of the frame. A constant force F starts pushing the frame into the magnetic field at t =0. (a) Find the acceleration of the frame when its speed has increased to v. (b) Show that after some time the frame will move with a constant velocity till the whole frame enters into the magnetic field. find this velocity v0. (c) show that the velocity at tiem t is given by v=v0(1−e−Ftmv0.
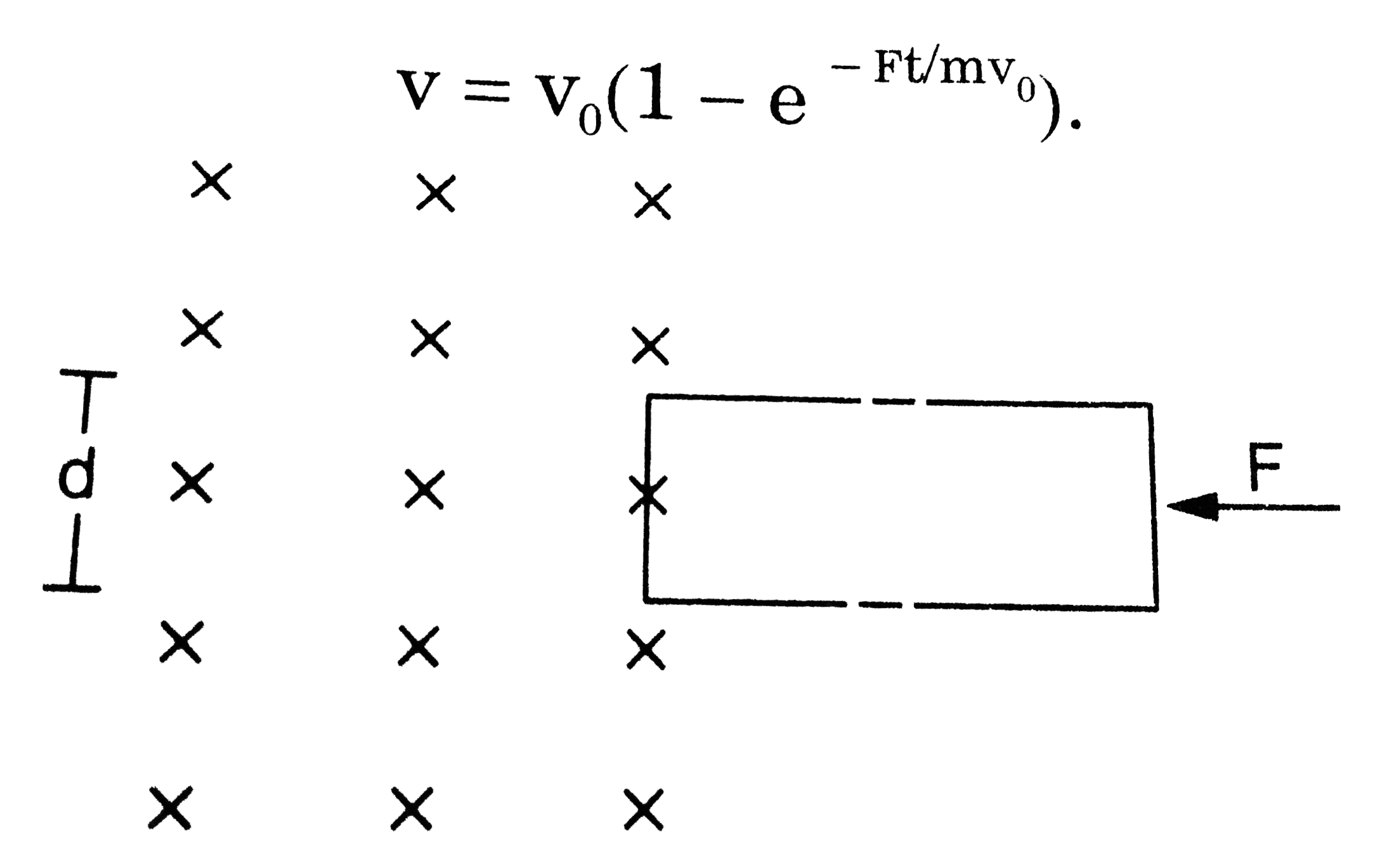 View Solution
View SolutionQuestion 44
Shows a smooth pair of thick metallic rails connected across a battery of emf ε having a negligible internal resistance. A wire ab of length l and resistance r can slide smoothly on the rails. The entire system lien in a horizontal plane and is immersed in a uniform vertical magnetic field B. At an instant t, the wire is given a small velocity v towards right. (a) find the current in it at this instant. What is the direction of the current? (b) What is the force acting on the wire at this instant? (c) Show that after some time the wire ab will slide with a constant velocity. Find this velocity.
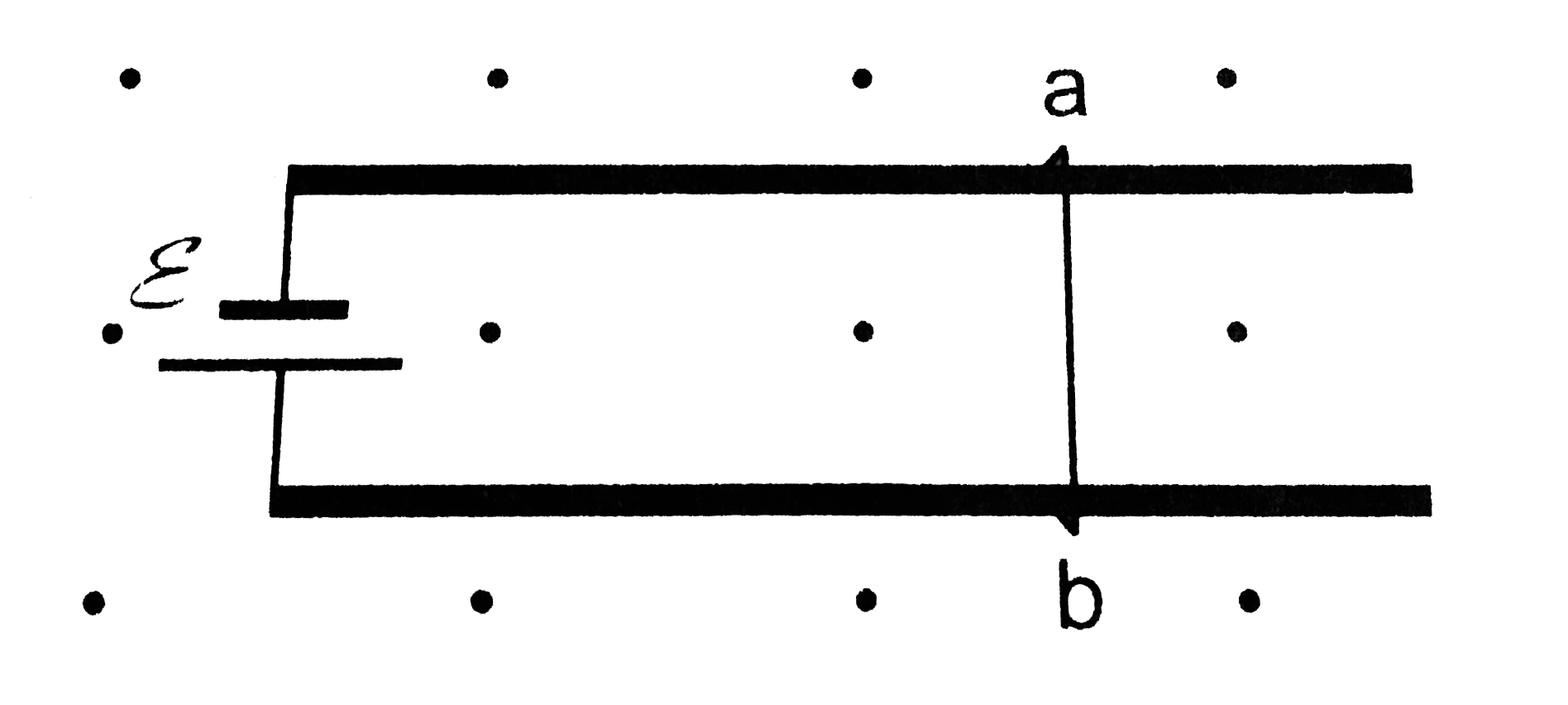 View Solution
View SolutionQuestion 45
A conducting wire ab of length l, resistance r and mass m starts sliding at t = 0 down a smooth, vertical, thick pair of connected rails as shown in . A uniform magnetic field B exists in the space in a diraction perpendicular to the plane of the rails. (a) Write the induced emf in the loop at an instant t when the speed of the wire is v. (b) what would be the magnitude and direction of the induced current in the wire? (c) Find the downward acceleration of the wire at this instant. (d) After sufficient time, the wire starts moving with a constant velocity. Find this velocity v_m. (e) Find the velocity of the wire as a function of time. (f) Find the displacement of the wire as a functong of time. (g) Show that the rate of heat developed inte wire is equal to the rate at which the gravitational potential energy is decreased after steady state is reached.
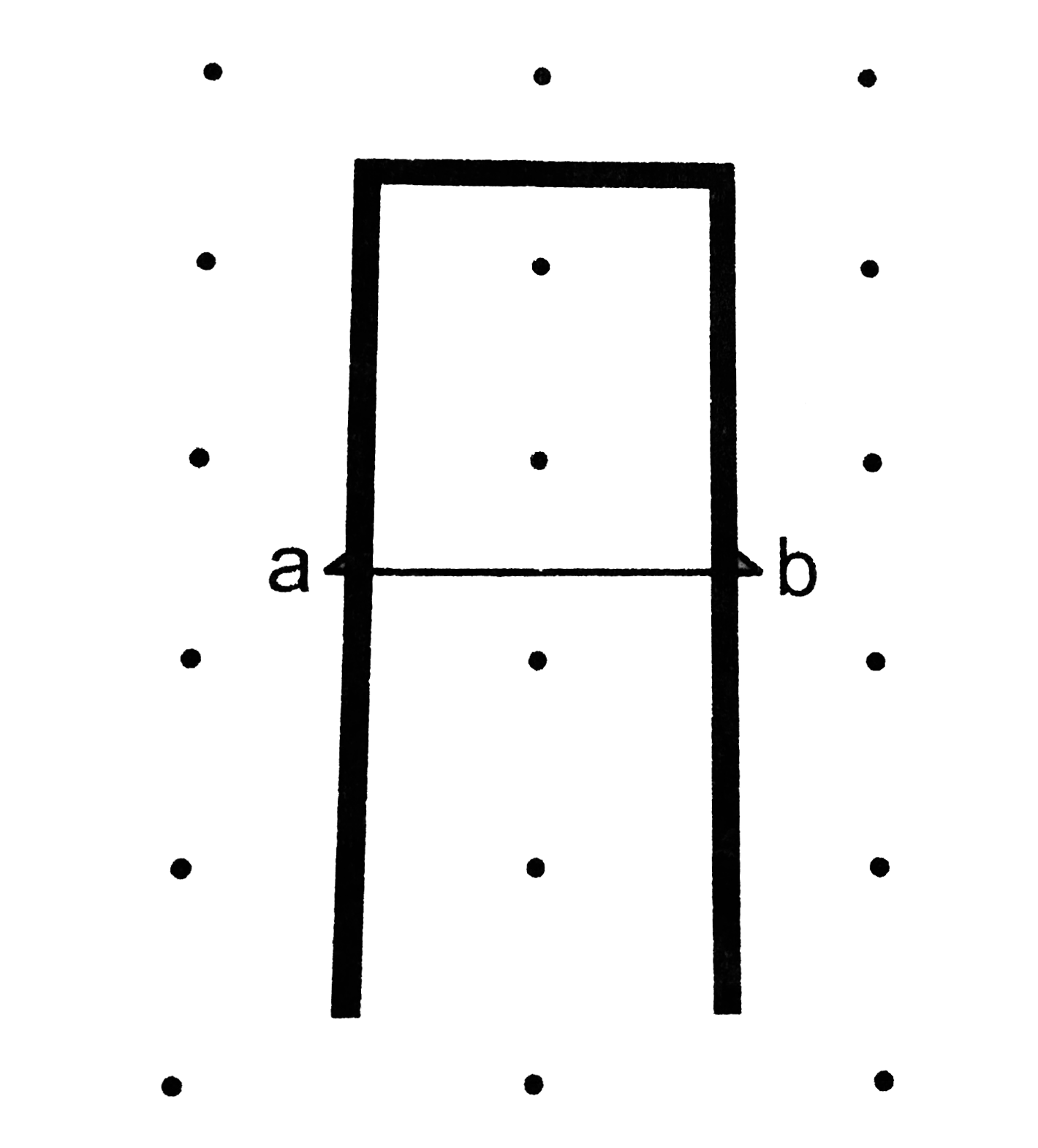 View Solution
View SolutionQuestion 46
A bicycle is resting on its stand in the east - west direction and the rear wheel is rotated at an angular speed of 100 revolutions per minute. If the length of each spoke is 30.0 cm and the horizontal component of the earth's magnetic field is 2.0×10−5T, find the emf induced between the axis and the outer end of a spoke. Neglect centripetal force acting on the free electrons of the spoke. View SolutionQuestion 48
shows a conducting disc rotating about its axis in a perpendicular magnetic field B. A resistor of resistance R is connected between the centre and the rim. Calculate the current in the resistor. Does it enter the disc or leave it at the centre? The radius of the disc is 5.0 cm , angular speed ω=10rads,B=0.40T and R=10Ω.
 View Solution
View SolutionQuestion 50
shows a straight, long wire carrying a current I and a rod of length l coplanar with the wire and perpendicular to it. The rod moves with a constant velocity v in a direction parallel to the wire. The distance of the wire from the centre of the rod is x. Find the motional emf induced in the rod.
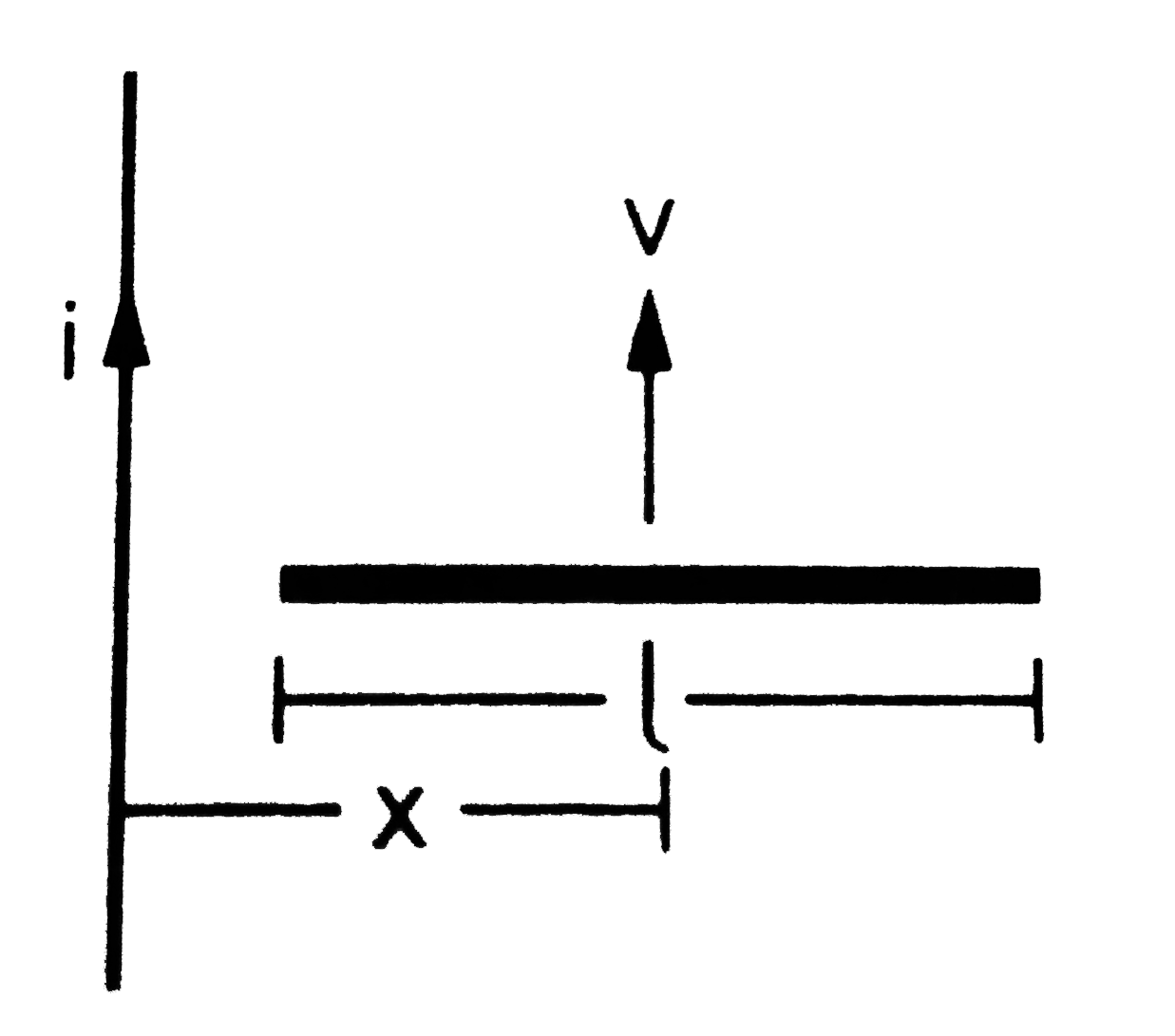 View Solution
View SolutionQuestion 51
Consider a situation similar ot that of the previous problem except that the ends of the rod slide on a pair of thick metallic rails laid parallel to the wire. At one end the rails are connected by resistor of resistance R. (a) what force is needed ot keep the rod sliding at a constant speed v? (b) in this situation what is the current in the resistance R? (c) Find the rate of heat developed in the resistor. (d) find the power delivered by the external agent exerting the force on the rod.View SolutionQuestion 52
Shows a square frame of wire having a total resistance r placed coplanarly with a long, straight wire. The wire carries a current I given by i=i0sinωt. Find(a) the flux of the magnetic field through the square frame, (b) the emf induced in the frame and (c) the heat developed in the frame in the time interval 0 to 20πω.
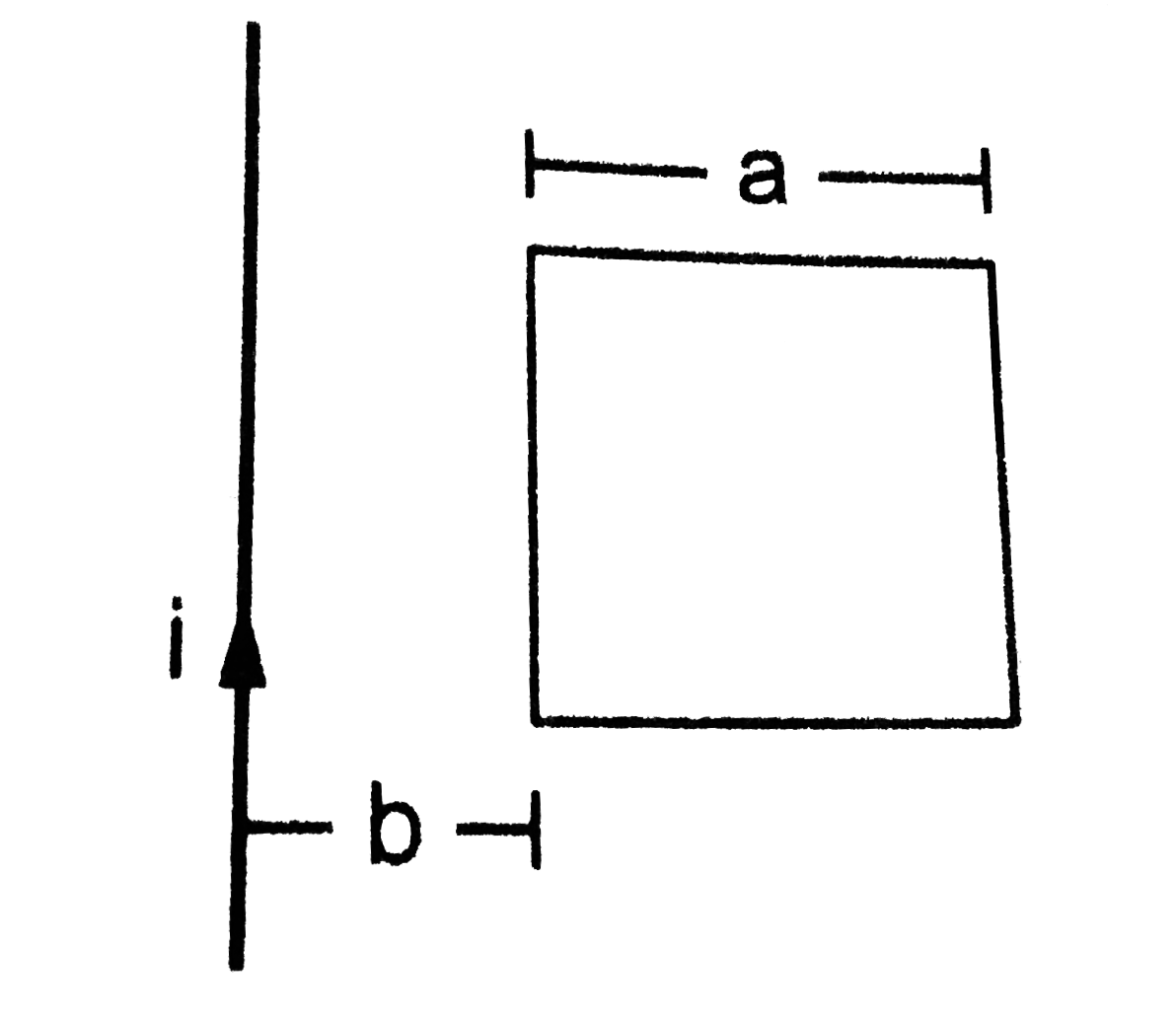 View Solution
View SolutionQuestion 53
A rectangular metallic loop of length l and width b is placed coplanerly with a long wire carrying a current I . The loop is moved perpendicular to the wire with a speed v in the plane containing the wire and the loop. Calculate the emf induced in the loop when the rear end of the loop is at a distance a from the wire. Solve by using Faraday's law for the flux through the loop and also by replacing different segments with equivalent batteries.
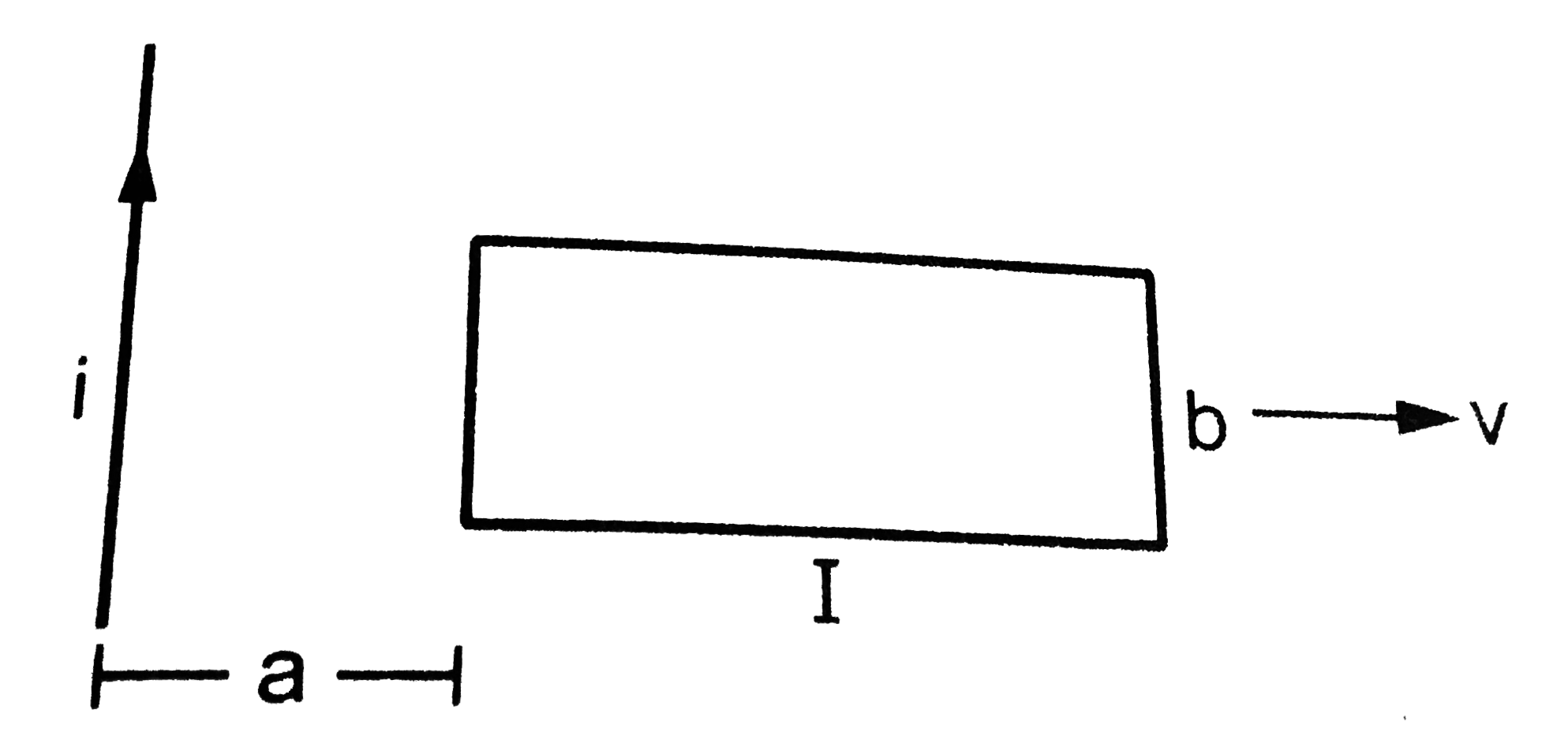 View Solution
View SolutionQuestion 54
Shows a conducting circular loop of radius a placed in a uniform, perpendicular magnetic field B. A thick metal rod OA is pivoted at the centre O. The other end of the rod touches the loop at A. The centre O and a fixed point C on the loop are connected by a wire OC of resistance R. A force is applied at the middle point of the rod OA perpendicularly, so that the rod rotates clockwise at a uniform angular velocity ω. Find the force.
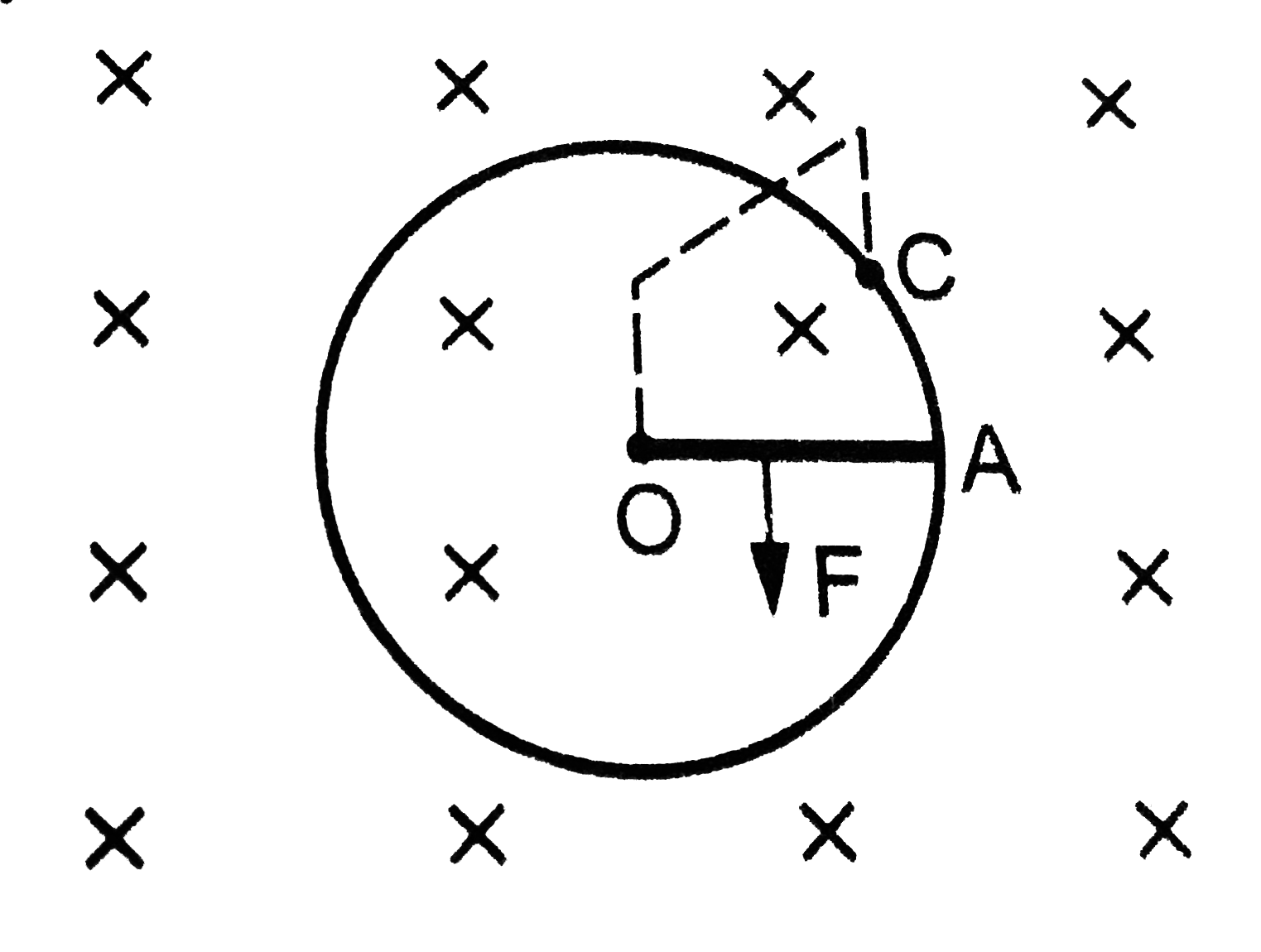 View Solution
View SolutionQuestion 55
Consider the situation shown in the figure o fthe previous problem. Suppose the wire connecting O and C has zero resistance but circular loop has a resistance R uniformly distributed along its length. The rod OA is made ot rotate with a uniform angular speed ω as shown in the figure. Find the current in the rod when <AOC=90∘. View SolutionQuestion 56
Consider a variation of the previous problem. Suppose the circular loop lies in a vertical plane. The rod has a mass m. The rod and the loop have negligible resistances but the wire connecting O and C has a resistance R. The rod is made to rotate with a uniform angular velocity ω in the clockwise direction by applying a force at the midpoint of OA in a dirction perpendicular ot it. find the magnitude of this force when the rod makes an angle θ with the vertical.View SolutionQuestion 57
Shows a situation similar to the previous problem. All parameters are the same except that a battery of emf ε and a variable resistance R are connected wires. Let θ be the angle made by the rod from the horizontal position (shown in the figurer), measuredin the clockwise direction. During the part of the motion O<θ<π4 the only forces acting on the rod are gravity and the forces exerted by the magnetic field and the pivot. However, during the part of the motion, the resistance R is varied in such a way that the rod continues to rotate with a constant angular velocity ω. Find the value of R in terms of the given quantities.
 View Solution
View SolutionQuestion 58
A wire of mass m and length l can slide freely on a pair of smooth, vertical rails. A magnetic field B exists in the region in the direction perpendicular to the plane of the rails. The rails are connected at the top end by a capacitor of capacitance C. Find the acceleration of the wire neglecting any electric resistance.
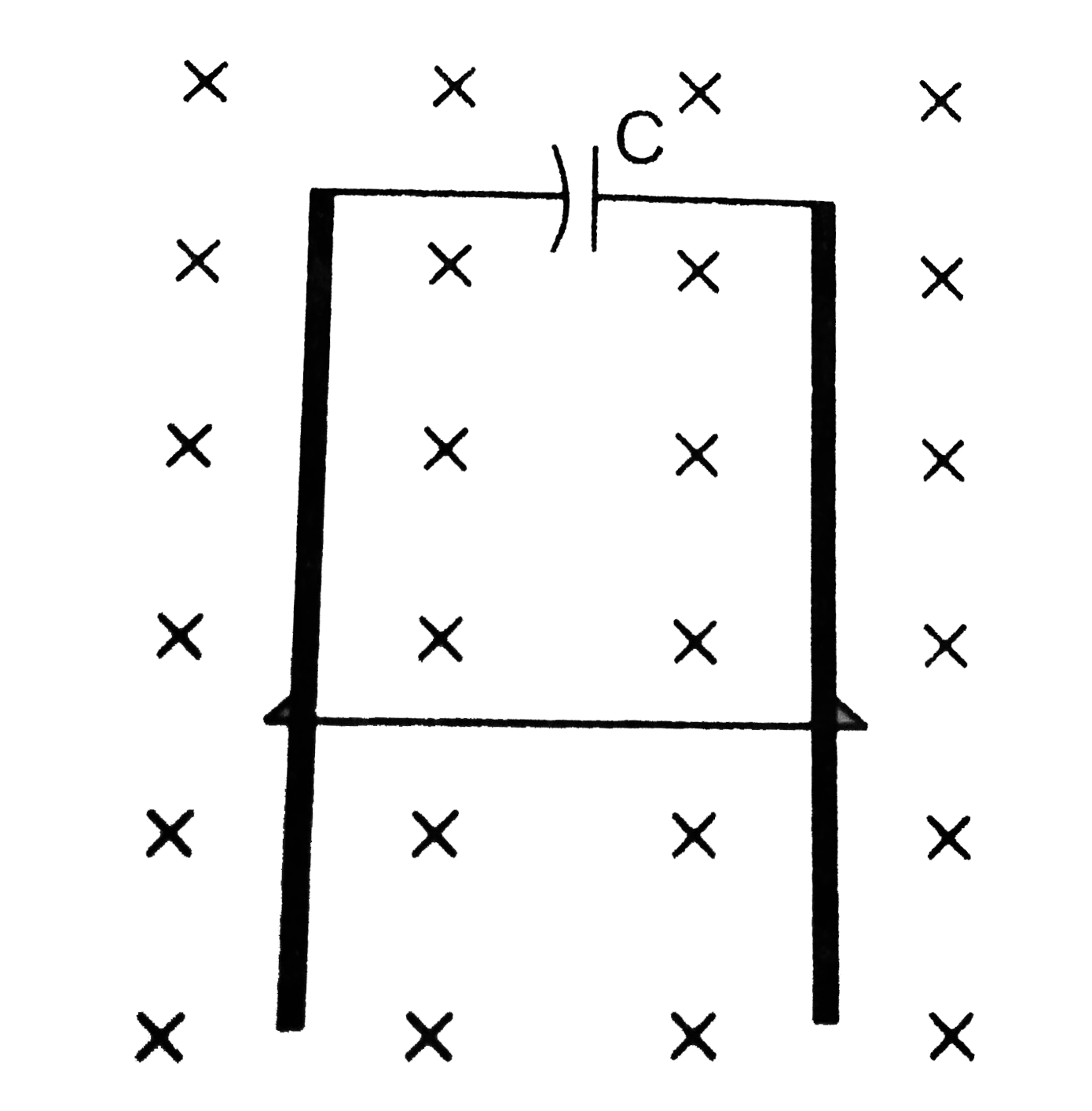 View Solution
View SolutionQuestion 59
A uniform magnetic field B exists in a cylindrical region, shown dotted in. The magnetic field increases at a constant rate dBdt Consider a circle of radius r coaxial with the cylindrical region. (a) find the magnitude of the electric field E at a point on the circumference of the circle. (b) Consider a point P on the side of the square circumscribing the circle. Show that the component of the induced electric field at P along ba is the same as the magnitude found in part(a).
 View Solution
View SolutionQuestion 60
The current in an ideal, long solenoid is varied at a uniform rate of 0.01As−1. The solenoid has 2000 turns/m and its radius 6.0 cm. (a) Consider a circle of radius 1.0 cm inside the solenoid with its axis coinciding with the axis of the solenoid. write the change in the magnetic flux through this circle in 2.0 seconds. (b) find the electric field induced at a point on the circumference of the circle. (c) find the electric field induced at a point outside the solenoid at a distance 8.0cm from its axis.View SolutionQuestion 75
A coil having an inductance L and a resistance R is connected to a battery of emfε. Find the time elapsed before (a) the current reaches half its maximum value, (b) the power dissipated in heat reaches half its maximum value and © the magnetic field energy stored in the circuit reaches half its maximum value.View SolutionQuestion 76
A solenoid having inductance 4.0 H and resistance 10 Omega is connected to a 4.0 V battery at t = 0. Find (a) the time constant, (b) the time elapsed before the current reached 0.63 of its steady state value, (c ) the power delivered by the battery at this instant and (d) the power dissipated in Joule heating at this instant. View SolutionQuestion 78
An LR circuit with emf ε is connected at t = 0. (a) find the charge Q which flows through the battery during O to t. (b) Calculate the work done by the battery during this period. (d) find the magnetic field energy stored in the circuit at time t. (e) Verify that the results in the three parts above are consistent with energy conservation.View SolutionQuestion 79
an inductor of inductance 2.00 H is joined in series with a resistor of resistance 200Ω and a battery of emf 2.00 V. At t = 10 ms, find (a) th current in the circuit, (b) the power delivered by the batter, (c ) the power dissipated in heating the resistor and (d) the rate at which energy is being stored in magnetic field.View SolutionQuestion 80
Two coil A and B have inductances 1.0 H and 2.0 H respectively. The resistance of each coil is 10Ω. Each coil is connected to an ideal battery of emf 2.0V at t=0. Let iA and iB be the current in the two circuit at time t. Find the raito iAIB at (a) t=100ms, (b) t=200ms and (c ) t=1s.View SolutionQuestion 82
A constant current exists in an inductor coil connected to a battery. The coil is short circuited and the battery is removed. Show that the charge flown through the coil aftter the short circuiting is the same as that which flows in one time constant before the short circuiting. View SolutionQuestion 83
Consider the circuit shown in .(a) find the current through the battery a long time after the switch S is closed. (b) Suppose the switch is again opened at t = 0. What is the time constant of the discharging circuit? (c ) Find t current through the inductor after one time constant.
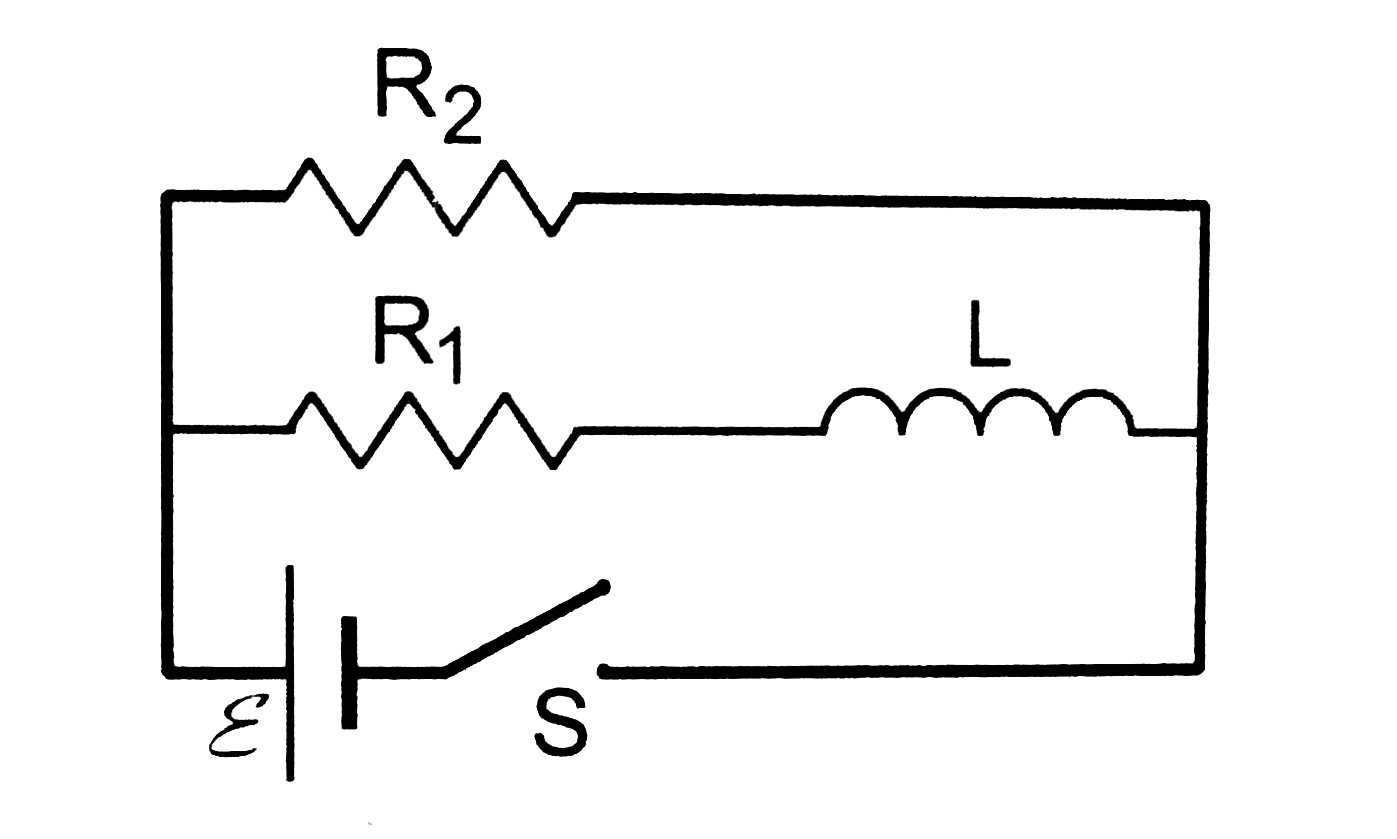 View Solution
View Solution