Mechanics Problems from IE IRODOV PHYSICS (HINGLISH) MECHANICS for Class 12
| Class 12 | PHYSICS |
| Chapter | MECHANICS |
| IE IRODOV PHYSICS (HINGLISH) | Mechanics Problems |
| Medium | English |
| Academic Year | 2023-2024 |
Question 3
A point mass starts moving in a straight line with a constant acceleration a. At a time t1 a fter the beginning of motion, the acceleration changes sign, remaining the same in magnitude. Determine the time t from the beginning of motion in which the point mass returns to the initial position.View SolutionQuestion 4
A small ball thrown at an initial velocity v0 at an angle α to the horizontal strikes elastically with a smooth vertical wall moving towards it at a horizontal velocity v and returns to the point from which it was thrown. Determine the time t from the beginning of motions to the moment of impact with vertical wall. Neglect friction losses.View SolutionQuestion 5
A cannot fires from under a shelter inclined at an angle α to the horizontal (Fig.). The cannot is at point A at a (distance l from the base of the shelter (point B). The initial velocity of the shell is v0, and its trajectory lies in the plane of the figure. Determine the maximum range Lmax of the shell.
 View Solution
View SolutionQuestion 6
The slopes of the windscreen of two motorcars are β1=30∘ and β2=15∘ respectively. At what ratio v1/v2 of the velocities of the cars will their drivers see the hailstones bounced by the windscreen of their cars in the vertical direction ? Assume that haistones fall vertically. View SolutionQuestion 7
An aeroplane flying along the horizontal at a velocity v0 starts to ascend, describing a circle in the vertical plane. The velocity of the plane changes with height h above the initial level of motion according to the law v2=v20−2a0h. The velcity of the plane at the upper point of the trajectory is v1=v0/2. Determine the acceleration a of the plane at the moment when its velocity is directed vertically upwards. View SolutionQuestion 8
An open merry-go-round rotates at an angular velocity ω. A person stands in it at a distance r from the rotational axis. It is raining, and the raindrops fall vertically at a velocity v0. How should the person hold an umbrella to protect himself from the rain in teh best way ? View SolutionQuestion 9
A bobbin rolls without slipping over a horizontal surface so that the velocity v of the end of the thread (point A) is directed along the horizontal . A board hinged at point B leans against the bobbin (Fig.) The inner and outer radii of the bobbin are r and R respectively. Determine the angular velocity ω of teh board as a function of an angle α.
 View Solution
View SolutionQuestion 10
A magnetic tape is wound on an emptyspool rotating at a constant angular velocity. The final radius rt of the winding was found to be three times as large as the initial radius r1 ( Fig. ). The winding time of the tape is t1. What is the time t2 required or winding a tape whose thickness is half that of the initial tape?
 View Solution
View SolutionQuestion 12
Two small rings O and O' are put on two vertical stationary rods AB and A'B', respectively. One end of an inextensible thread is tied at point A'. The thread passes through ring O' and its other end is tied to ring O. Assuming that ring O' moves downwards at a constant velocity v1, then velocity v2 of the ring O, when ∠AOO'=α is
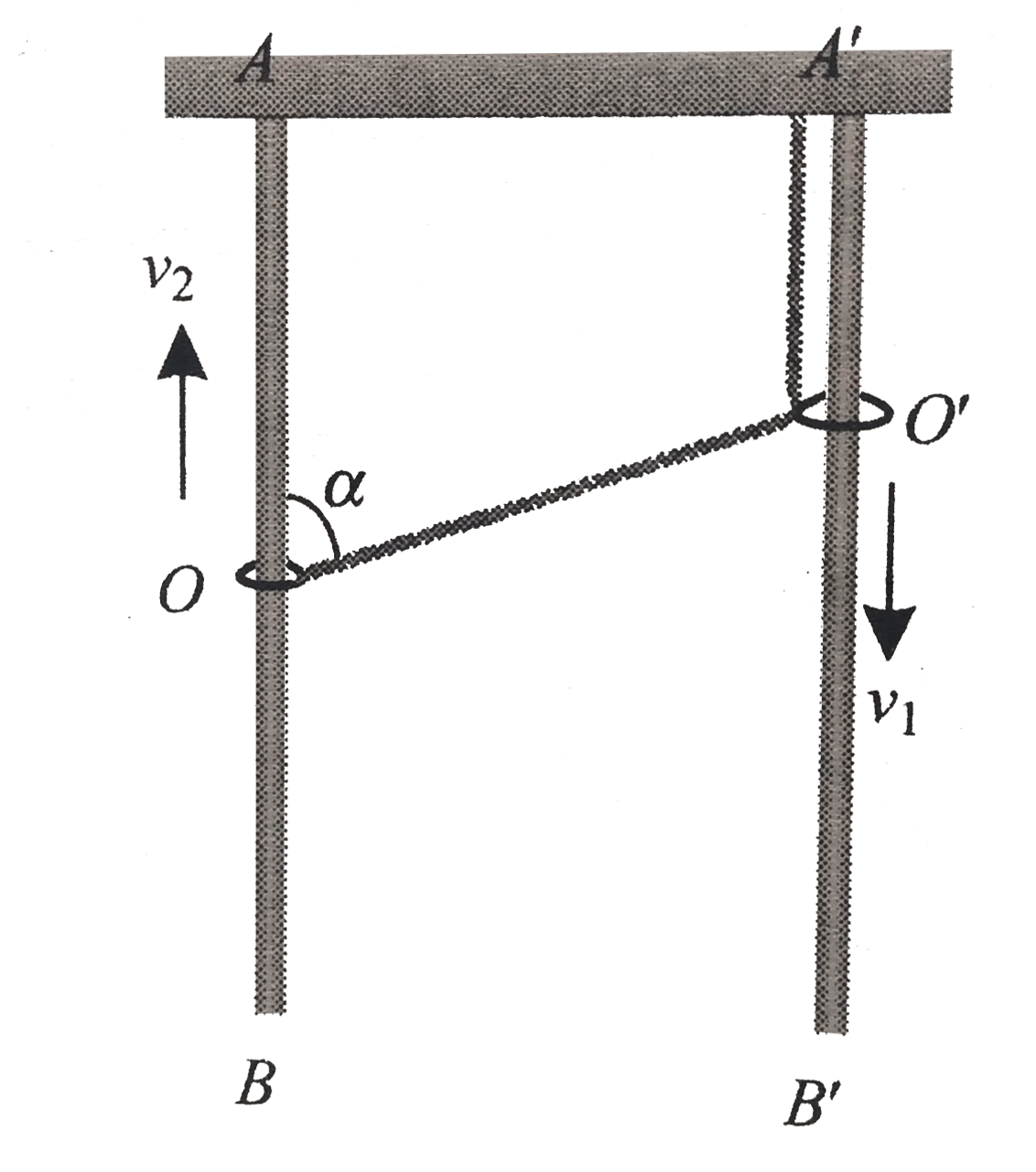 View Solution
View SolutionQuestion 13
A weightless inextensible rope rests on a stationary wedge forming an angle α with a horizontal One end of the rope is fixed to the wall to point A.A small load is attached to the rope at point B The wedge starts moving to the right with a constant acceleration a The acceleration of the load is given by
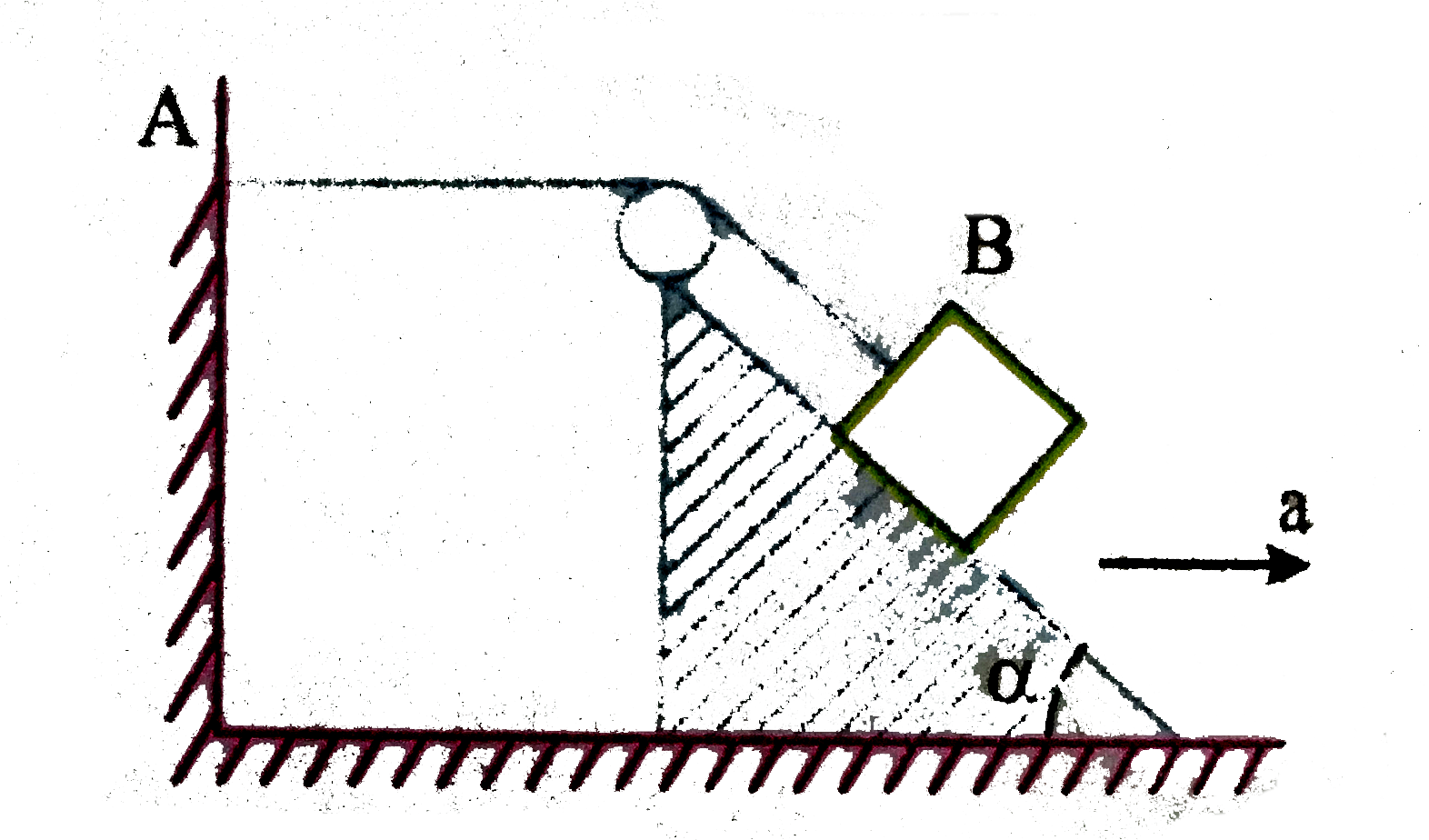 .View Solution
.View SolutionQuestion 14
An ant runs from an ant-hill in a straight line so that its velocity is inversely proportional to the distance from the centre of the ant-hill. When the ant is at point A at a distance l1=1m from the centre of the ant-hill, its velocity v1=2cm/s. What time will it take the ant to run from point A to point B which is at a distance l2=2m from the centre of the anthill ? View SolutionQuestion 15
During the motion of a locomotive in a circular path of radus R, wind is blowing in the horizontal direction. The trace left by the smoke is shown in Fig. (topview.) Using the figure, determine the velocity vwind of the wind if it is known to be constant, and if the velocity v10c of the loco-motive is 36km/h.
 View Solution
View SolutionQuestion 16
Three schoolboys, Sam, John, and Nick, are on merry-go-round. Sam and John occupy diametrically opposite points on a merry-go-round of radius r. Nick is on another merry-go-round of radius R. The positions of the boys at the initial instant are shown in Fig. Considering that the merry-go-round touch each other and rotate in the same direaction at the same angular velocity ω, determine the nature of motion of Nick from John's point of view and of Sam from Nick's point of view.
 View Solution
View SolutionQuestion 17
A hoop of radius R rests on a horizontal surface. A similar hoop moves past it at a velocity v. Determine the velocity vA of the upper point of "intersection" of the hoops as a function of the distance d between their centres, assuming that the hoops are thin, and the second hoop is in contact with the first hoop as it moves past the latter. View SolutionQuestion 19
The free end of a thread wound on a bobbin is passed round a nail A hammered into the wall. The thread is pulled at a constant velocity 'v' . Assuming pure rolling of bobin, find the velocity v0 of the centre of the bobbin at the instant when the thread forms an angle α with the vertical: (R and r are outer and inner radii off the babbin)
 View Solution
View SolutionQuestion 20
A rigid ingot is pressed between two parallel guides moving in horizontal directions at opposite velocities v1 and v2. At a certain instant of time, the points of contact between the ingot and the guides lie on a straight line perpendicular to the directions of velocities v1 and v2 (Fig). What points of teh ingot have velocities equal in magnitude to v1 and v2 at this instant ?
 View Solution
View SolutionQuestion 21
A block lying on a long horizontal conveyer belt moving at a constant velocity receives a velocity v0=5m/s relative to the ground in the direction opposite to the direction of motion of the conveyer. After t=4s, the velocity of the block becomes equal to the velocity of the belt. The coefficient of friction between the block and the belt is μ=0.2. Determine the velocity v of the conveyer belt. View SolutionQuestion 22
A body with zero initial velocity slips from the top of an inclined plane forming an angle α with the horizontal. The coefficient of friction μ between the body and the plane increases with the distance l from the top according to the law μ=bl. The body stops before it reaches the end of the plane. Determine the time t from the beginning of motion of the body to the moment when it comes to rest. View SolutionQuestion 23
A rope is passed round a stationary horizontal log fixed at a certain height above the ground. In order to keep a load of mass m=6 kg suspended on one end of the rope, the maximum force T1=40N should be applied to the other end of the rope. Determine the minimum force T2 which must be applied to the rope to lift the load. View SolutionQuestion 25
A certain constant force starts acting on a body moving at a constant velocity v. After a time interval Δt, the velocity of the body is reduced by half, and after the same time interval, the velocity is again reduced by half. Determine the velocity vf of the body after a time interval 3Δt from the moment when the constant force starts acting. View SolutionQuestion 26
Two identical weightless rods are hinged to each other and to a horizontal beam (Fig.). The rigidity of each rod is k0, and the angle between them is 2α. Determine the rigidity k of the system of rods relative to the vertical displacement of a hinge A under the action of a certain force F, assuming that displacements are small in comparison with the length of the rods.
 View Solution
View SolutionQuestion 27
Two heavy balls are simultaneously shot from two spring toy-guns arranged on a horizontal plane at a distance s = 10 m from each other. The first ball has the initial vertical velocity v1=10m/s, while the second is shot at an angle α to the horizontal at a velocity v2=20m/s. Each ball experiences the action of the force of gravity and the air drag F=μv,μ,=0.1g/s. Determine the angle cc at which the balls collide in air.View SolutionQuestion 29
A heavy ball of mass m is tied to a weightless thread of length 1. The friction of the ball against air is proportional to its velocity relative to the air: Flr=μv. A strong horizontal wind is blowing at a constant velocity v. Determine the period T of small oscillations, assuming that the oscillations of the ball attenuate in a time much longer than the period of oscillations.View SolutionQuestion 31
For the system at rest shown in Fig., determine the accelerations of all the loads immediately after the lower thread keeping the system in equilibrium has been cut. Assume that the threads are weightless and inextensible, the springs are weightless, the mass of the pulley is negligibly small, and there is no friction at the point of suspension.
 View Solution
View SolutionQuestion 32
A person hoists one of two loads of equal mass at a constant velocity v (Fig). At the moment when the two loads are at the same height h, the upper pulley is released (is able to rotate without friction like the lower pulley). Indicate the load which touches the floor first after a certain time t, assuming that the person continues to slack the rope at the same constant velocity v. The masses of the pulleys and the ropes and the elongation of the ropes should be neglected.
 View Solution
View SolutionQuestion 33
A block can slide along an inclined plane in various directions (Fig. ). If it receives a certain initial velocity v directed downwards along the inclined plane, its motion will be uniformly decelerated, and it comes to rest after traversing a distance l1. if the velocity of the same magntude is imparted to it in the upwards direction it comes to rest after traversing a distance l2. At the botton of the inclined plane, a perfectly smooth horizontal guide is fixed. Determine the distance 1 traversed by the block over the inclined plane along the guide if the initial velocity of the same magnitude is imparted to it in the horizontal direction?
 View Solution
View SolutionQuestion 34
A block is pushed upwards along the roof forming an angle a with the horizontal. The time of the ascent of the block to the upper point was found to be half the time of its descent to the initial point. Determine the coefficient of friction lit between the block and the roof.View SolutionQuestion 35
Two balls are placed as shown in Fig. on a "weightless" support formed by two smooth inclined planes each of which forms an angle α with the horizontal. The support can slide without friction along a horizontal plane. The upper ball of mass m1 i s released. Determine the condition under which the lower ball of mass m2 tarts "climbing" up the support.
 View Solution
View SolutionQuestion 36
A cylinder of mass m and radius r rests on two supports of the same height (Fig. ). One support is stationary, while the other slides from under the cylinder at a velocity v. Determine the force of normal pressure N exerted by the cylinder on the stationary support at the moment when the distance between points A and B of the supports is Ab=r√2, assuming that the supports wery very close to each other at the initial instant. The friction between the cylinder and the supports should be neglected.
 View Solution
View SolutionQuestion 37
cylinder and a wedge with a vertical face, touching each other, move along two smooth inclined planes forming the same angle α with the horizontal (Fig. ). The masses of the cylinder and the wedge are m1 and m2 respectively. Determine the force of normal pressure N exerted by the wedge on the cylinder, neglecting the friction between them.
 View Solution
View SolutionQuestion 38
A weightless rod of length l with a small load of mass m at the end is hinged at point A (Fig.) and occupies a strictly vertical position, touching a body of mass M. A light jerk sets the system in motion . For what mass ratio M/m will the rod form an angle α=π/6 with the horizontal at the moment of the separation from the body ? What will be the velocity u of the body at this moment ? Friction should be neglected.
 View Solution
View SolutionQuestion 39
A homogeneous rod AB of mass m and length l leans with its lower end against the wall and is kept in the inclined positions by a string DC (Fig). The string is tied at point C to the wall and at point D to the rod so that AD=AB/3. The angles formed by the string and the rod with the wall are α and β respectively. Find all possible values of the coefficient of friction μ between the rod and the wall.
 View Solution
View SolutionQuestion 40
Two rigidly connected homogeneous rods of the same length and mass m1 and m2 respectively form an angle π/2 and rest on a rough horizontal surface (Fig.) The system is uniformly pulled with the help of a string fixed to the vertex of the angle and parallel to the surface. Determine the angle α formed by the string and the rod of mass m1.
 View Solution
View SolutionQuestion 41
A ball moving at a velocity v=10m/s hits the foot of a football player. Determine the velocity u with which the foot should move for the ball impinging on it to come to a halt, assuming that the mass of the ball is much smaller than the mass of the foot and that the impact is perfectly elastic.View SolutionQuestion 42
A body of mass m freely falls to the ground. A heavy bullet of mass M shot along the horizontal hits the falling body and sticks in it. How will the time of fall of the body to the ground change? Determine the time t of fall if the bullet is known to hit the body at the moment it traverses half the distance, and the time of free fall from this height is to. Assume that the mass of the bullet is much larger than the mass of the body (M>>m). The air drag should be neglected. View SolutionQuestion 44
Two identical wedges of mass M are smoothly conjugated . The wedges are free to move on a smooth horizonal surface, A block of mass m is releaded from a height h on one of the wedge (See fig 4E.9)
(a) Show that the height h to which the mass m ascends the right wedge is hmax=M2(M+m)2h.
(b) what mass ratio (M/m) results is hmax=h/4
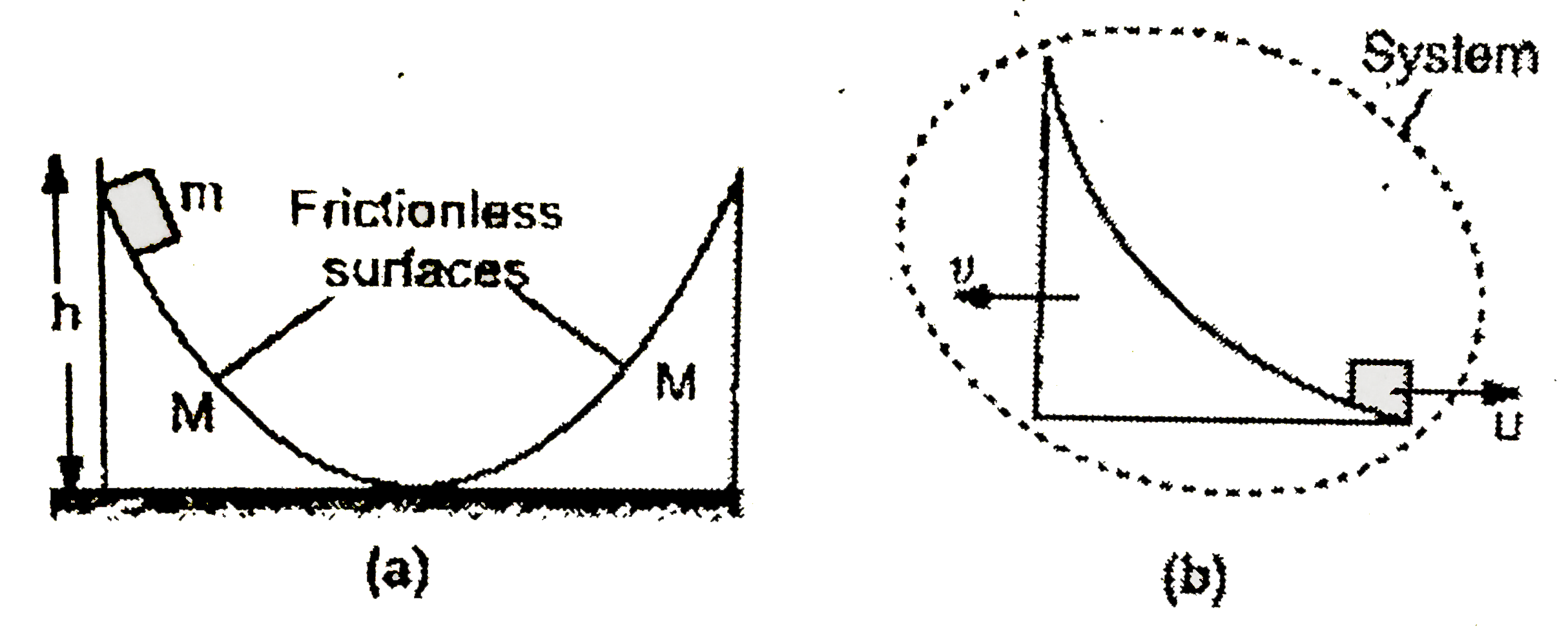 View Solution
View SolutionQuestion 45
A wedge of mass m1 with its upper surface hemispherical in shape, as shown in Fig. 4E.7(a), rests on a smooth horizontal surface near the wall. A small block of mass m2 slides without friction on the hemispherical surface of the wedge. What is the maximum velocity attained by the wedge ?
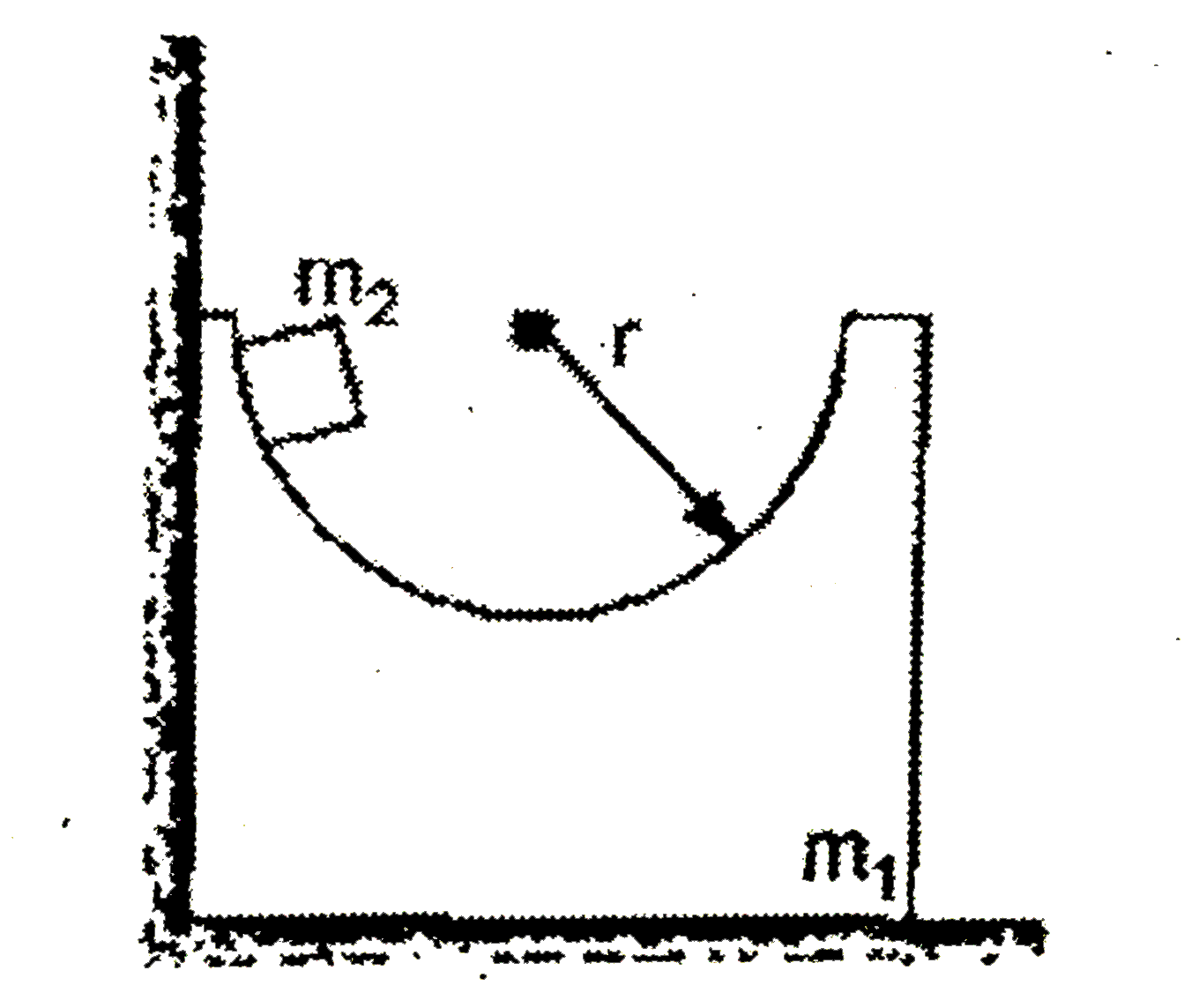 View Solution
View SolutionQuestion 46
A round box of inner diameter D containing a washer of radius r lies on a table (Fig). The box is moved as a whole at a constant velocity v directed along the lines of centres of the box and the washer. At an instant t0, the washer hits the box. Determine the time dependeces of the displacement xwash of the waher and of its velocity vwash relative to the table, starting from the instant t0 and assuming that all the impacts of the washer against the box are perfectly elastic. Plot the graphs xwash(t) and vwash(t). The friction between the box and the washer should be neglected.
 View Solution
View SolutionQuestion 47
A thin hoop of mass M and radius r is placed on a horizontal plane. At the initial instant, the hoop is at rest. A small washer of mass m with zero initial velocity slides from the upper point of the hoop along a smooth groove in the inner surfaces of the hoop. Determine the velocity u of the centre of the hoop at the moment when the washer is at a certain point A of the hoop, whose radius vector forms an angle ϕ with the vertical (figure). The friction between the hoop and the plane should be neglected
 View Solution
View SolutionQuestion 48
A horizontal weightless rod of length 3l is suspended on two vertical strings. Two loads of mass m1 and m2 are in equilibrium at equal distance from each other and from the ends of the strings (Fig). Determie the tension T of the left string at the instant when the right string snaps.
 View Solution
View SolutionQuestion 49
A ring of mass m connecting freely two identical thin hoops of mass M each starts sliding down. The hoops move apart over a rough horizontal surface. Determine the acceleration a of the ring at the initial instant if ∠AO1O2=α (Fig), neglecting the friction between the ring and the hoops.
 View Solution
View SolutionQuestion 50
A flexible pipe of length l connects two points A and B in space with an altitude difference h (Fig). A rope passed through the pipe is fixed at point A. Determine the initial acceleration a of the rope at the instant when it is released, neglecting the friction between the rope and the pipe walls.
 View Solution
View SolutionQuestion 51
A smooth washer impinges at a velocity 'v' on a group of three smooth identical blocksresting on a smooth horizontal surface as shown in fig. Mass of each block is equal to mass of the washer. The diameter of the washer and its height are equal to edge of the block. The velocity of blocks (2) and (3) after collision is
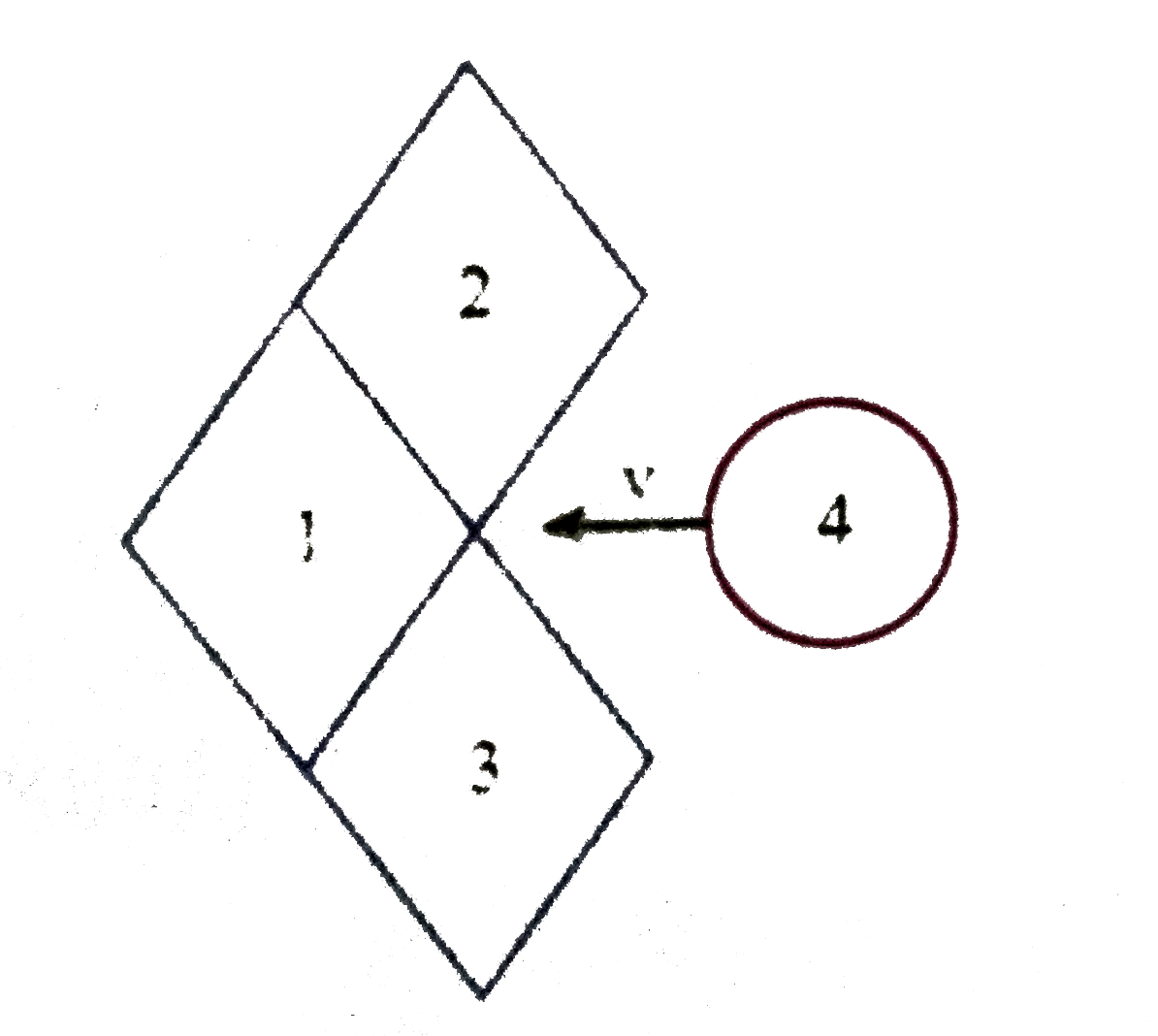 View Solution
View SolutionQuestion 52
Several identical balls are at rest in a smooth stationary horizontal circular pipe. One of the balls explodes, distintegrating into two fragments of different masses. Determine the final velocity of the body formed as a result of all collisions, assuming that the collisions are perfectly inelastic. View SolutionQuestion 53
Three small bodies with the mass ratio 3 : 4: 5 (the mass of the lightest body is m) are kept at three different points on the inner surface of a smooth hemispherical cup of radius r. The cup is fixed at its lowest point on a horizontal surface. At a certain instant, the bodies are released. Determine the maximum amount of heat Q that can be liberated in such a system.At what initial arrangement of the bodies will the amount of liberated heat be maximum ? Assume that collisions are perfectly inelastic. View SolutionQuestion 55
A long smooth cylindrical pipe of radius r is tilted at an angle α to the horizotal (Fig). A small body at point A is pushed upwards along the inner surface of the pipe so that the direction of its initial velocity forms an angle φ with generatrix AB. Determine the minimum initial velocity v0 at which the body starts moving upwards without being separated from the surface of the pipe.
 View Solution
View SolutionQuestion 56
An inextensible rope tied to the axle of a wheel of mass m and radius r is pulled in the horizontal direction in the plane of the wheel. The wheel rolls without jumping over a grid consisting of parallel horizontal rods arranged at a distance 1 from one another (1<r). Determine the average tension T of the rope at which the wheel moves at a constant velocity v, assuming the mass of the wheel to be concentrated at its axle.View SolutionQuestion 57
A thin rim of mass m and radius r rolls down an inclined plane of slope α, winding thereby a thin ribbon of linear denstiy ρ (Fig). At the initial moment, the rim is at a height h above the horizontal surface. Determine the distance s from the foot of the inclined plane at which the rim stops, assuming that the inclined plane smoothly changes into the horizontal plane.
 View Solution
View SolutionQuestion 59
A ball is tied by a weightless inextensible thread to a fixed cylinder of radius r. At the initial moment the thread is wound so that the ball touches the cylinder. Then the ball acquires a velocity v in the raidal direction, and the thread starts unwinding (Fig). Determine the length l of the upwound segment of the thread by the instant of time t, neglecting the force of gravity.
 View Solution
View SolutionQuestion 60
Three small balls of the same mass, white (w), green (g), and blue (b), are fixed by weightless rods at the vertics of the equilateral triangle with side l. The system of balls is placed on a smooth horizontal surface and set in rotation about the centre of mass with period T. At a certain instant, the blue ball tears away from the frame. Determine teh distance L between the blue and the green ball after the time T. View SolutionQuestion 61
A block is connected to an identical block through a weightless pulley by a weightless inextensible thread of length 2l (Fig). The left block rests on a table at a distance l from its edge, while the right block is kept at the same level so that the thread is unstretched and does not sag, and then released. What will happen first will the left block reach the edge of the table (and touch the pulley) or the right block hit and table?
 View Solution
View SolutionQuestion 62
Two loads of the same mass are tied to the ends of a weightless inextensible thread passed through a weightless pulley (Fig. ). Initially, the system is at rest,and the loads are at the same level. Then the right load abruptly acquires a horizontal velocity v in the plane of the figure. Which load will be lower in a time?
 View Solution
View SolutionQuestion 64
A weightless horizontal rigid rod along which two balls of the same mass m can move without friction rotates at a constant angular velocity ω about a vertical axle. The balls are connected by a weightless spring of rigidity k, whose length in the undeformed state is l0. The ball which is closer to the vertical axle is connected to it by he same spring. Determine the lengths of the springs. Under what conditions will be balls move in circles ? View SolutionQuestion 65
A conveyed belt of length lis moving with velocity v.a block of mass is pushed against the motion of conveyed belt with velocity v0 form end B Co- efficient of friction between block and belt is u the value of v0 so that the amount of heat liberated as a result of retardation of the block by conveyed belt is maximum is
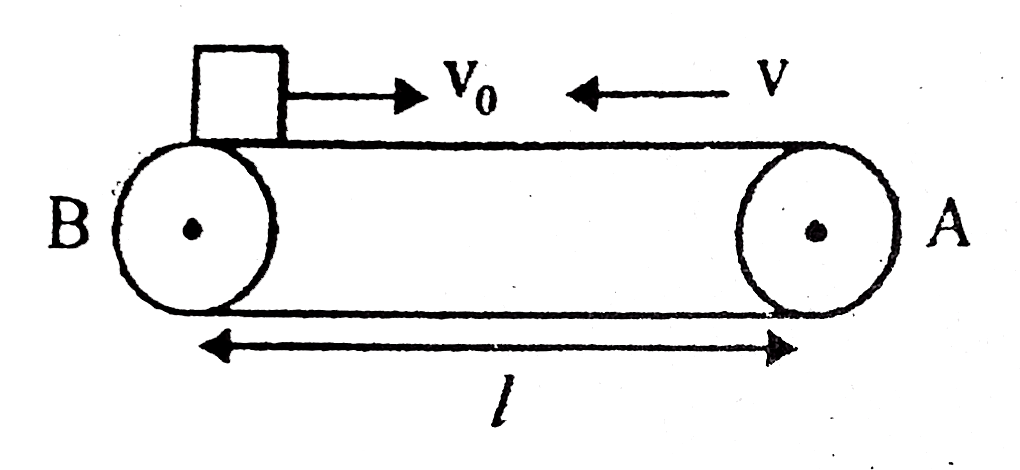 View Solution
View SolutionQuestion 66
A heavy pipe rolls from the same height down two hills with different profiles (Figs.) In the former case, the pipe rolls down without slipping, while in the latter case, it slips on a certain region. In what case will the velocity of the pipe at the end of the path be lower ?
 View Solution
View SolutionQuestion 69
A meteorite approaching a planet of mass M (in the straight line passing through the centre of the planet) collides with an automatic space station orbiting the planet in a circular trajectory of radius R. The mass of the station is ten times as large as the mass of the meteorite. As a result of the collision, the meteorite sticks in the station which goes over to a new orbit with the minimum distance R/2 from the planet. Speed of the meteorite just before it collides with the planet is : .View SolutionQuestion 70
The cosmonauts who landed at the pole of a planet found that the force of gravity there is 0.01 of that on the Earth, while the duration of the day on'the planet is the same as that on the Earth. It turned out besides that the force of gravity on the equator is zero. Determine the radius R of the planet. View SolutionQuestion 72
Three loads of mass m1,m2 and M are suspended on a string passed through two pulleys as shown in Fig. The pulleys are at the same distance from the points of suspension. Find the ratio of masses of the loads at which the system is in equilibrium. Can these conditions always be realized? The friction should be neglected.
 View Solution
View SolutionQuestion 74
Three weightless rods of length 1 each are hinged at points A and B lying on the same horizontal and joint through hinges at points C and D (Fig. ). The length AB=2l. A load of mass m is suspended at the hinge C. Determine the minimum force Fmin aplied to the hinge D for which the middle rod remains horizontal.
 View Solution
View SolutionQuestion 75
A homogeneous rod of length 2l leans against a vertical wall at one end and against a smooth stationary surface at another end. What function y (.x) must be used to describe the cross section of this surface for the rod to remain in equilibrium in any position even in the absence of friction? Assume that the rod remains all the time in the same vertical plane perpendicular to the plane of the wall. View SolutionQuestion 76
A ball is suspended by a thread of length l at the point O on an incline wall as shown. The inclination of the wall with the vertical is α.The thread is displaced through a small angle β away from the vertical and the ball is released. Find the period of oscillation of pendulum.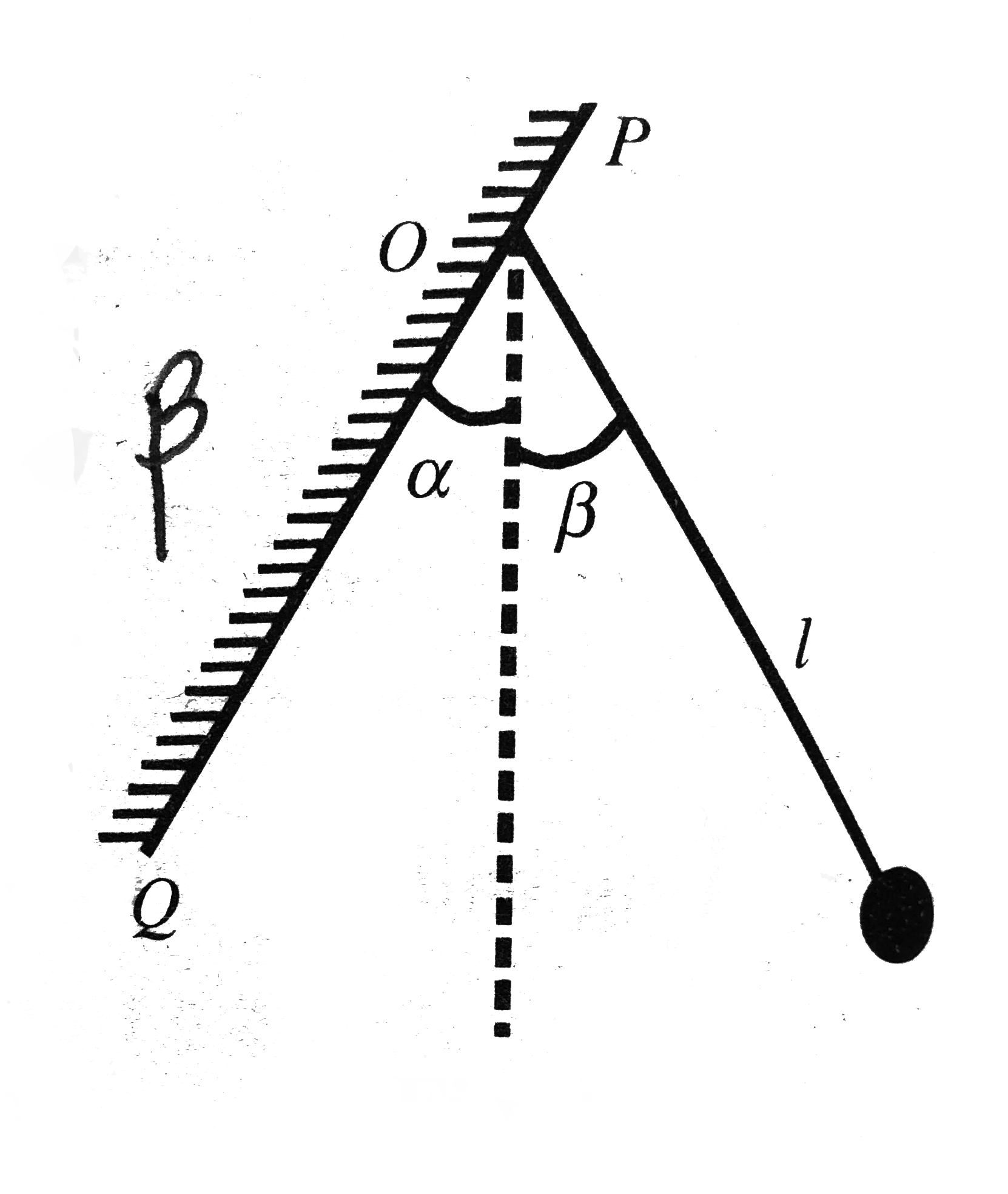
Consider both cases
a. α>β
b. α<β
Assuming that any impact between the wall and the ball is elastic.View SolutionQuestion 77
A ball of mass m falls from a certain height on the pan of mass M(M>>m) of a spring balance. The rigidity of the s prin is k. Determine the displacement Δx of the point about which the pointer of the balance will oscillate, assuming that the collisions of the ball with the pan are erfectly elastic.View SolutionQuestion 78
A bead of mass m can move without friction along a long wire bent in a vertical plane in the shape of a graph of a certain function. Let lA be the length of the segment of the wire from the origin to a certain point A. It is knonw that if the bead is released at point A such that lA<lA0, its motion will be strictly harmonic l(t)=lAcosωt. Prove that there exists a point B(lA0<<lB) at which the condition of harmonicity of oscillations will be violated. View SolutionQuestion 80
A heavy round log is suspended at the ends on two ropes so that the distance between the points of suspension of the ropes is equal to the diameter of the log. The length of each vertical segment of the ropes is 1. Determine the period T of small oscillations of the system in a vertical plane perpendicular to the log.View SolutionQuestion 81
A load of mass M is on horizontal rails. A pendulum made of a ball of mass m tied to a weightless inextensible thread is suspended to the load. The load can move only along the rails. Determine the ratio of the periods T2/T1 of small oscillations of the pendulum in vertical planes parallel and perpendicular to the rails. View SolutionQuestion 82
Four weightless rods of length l each are connected by hinged joints and form a rhomb (Fig). A hinge A is fixed, and a load is suspended to a hinge C. Hinges D and B are connected by a weightless spring of length 1.5l in the undeformed state. In equilibrium, the rods form angles α0=30∘ with the vertical. Determine the period T of small oscillations of the load.
 View Solution
View SolutionQuestion 83
A weightless rigid rod with a load at the end is hinged at point A to the wall so that it can rotate in all directions (Fig).
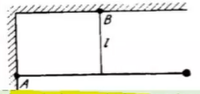
The rod is kept in the horizontal position by a vertical inextensible thread of length 1, fixed at its midpoint. The load receives a momentum in the direction perpendicular to the plane of the figure.
Determine the period T of small oscillations of the system.View SolutionQuestion 84
One rope of a swing is fixed above the other rope by b. The distance between the poles of the swing is a. The lengths l1 and l2 of the ropes are such that l21+l22=a2+b2 (Fig ).
Determine the period T of small oscillations of the swing, neglecting the height of the swinging person in comparison with the above lengths.
 View Solution
View SolutionQuestion 85
Being a punctual man, the lift operator of a skyscraper hung an exact pendulum clock on the lift wall to know the end of the working day. The lift moves with an upward and downward accelerations during the same time (according to a stationary clock), the magnitudes of the accelerations remaining unchanged.
Will the operator finish his working day in time, or will he work more (less) than required?View SolutionQuestion 86
An aluminium wire is wound on a piece of cork of mass mcork. The densities ρcork, ρa1, and ρw, of cork, aluminium, and water are 0.5×103kg/m3,2.7×103kg/m3, and 1×103kg/ms respectively. Determine the minimum mass ma t of the wire that should be wound on the cork so that the cork with the wire is completely submerge 1 in water.View SolutionQuestion 87
One end of an iron chain is fixed to a sphere of mass M = 10 kg and of diameter D = 0.3 m (the volume of such a sphere is V=0.0141m3), while the other end is free. The length 1 of the chain is 3 m and its mass m is 9 kg. The sphere with the chain is in a reservoir whose depth H=3m.
Determine the depth at which the sphere will float, assuming that iron is 7.85 times heavier than water.View SolutionQuestion 92
A jet plane having a cabin of length = 50 m flies along the horizontal with an acceleration a=1m/s2. The air density in the cabin is ρ=1.2×10−3g/cm3.
What is the difference between the atmospheric pressure and the air pressure exerted on the ears of the passengers sitting in the front, middle, and rear parts of the cabin?View Solution


