Electromagnetic Induction from IE IRODOV PHYSICS Chapter 4 ELECTRODYNAMICS for Class 12
| Class 12 | PHYSICS |
| Chapter | ELECTRODYNAMICS |
| IE IRODOV PHYSICS | Electromagnetic Induction |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
A wire bent as a parabola y=ax2 is located in a uniformed magnetic field of induaction B , the vector B being perpendicular to the plane x−y . At moment t=0 a connector starts sliding translationwise from the parabola apex with a constant acceleration ω . Find the emf of electromagnetic induction in the loop thus formed as a function of y
 View Solution
View SolutionQuestion 2
A rectangular loop with a sliding connector of length l is located in a uniform magnetic field perpendicular to the loop plane. The magnetic induction is equal to B. The connector has an electric resistance R, the sides ab and cd have resistances R1 and R2. Neglecting the self-inductance of the loop, find the current flowing in the connector during its motion with a constant velocity v.
 View Solution
View SolutionQuestion 3
A metal disc of radius R=25cm rotates with a constant angular velocity ω = 130 rad s−1 about its axis. Find the potential difference between the center and rim of the disc if
(a) the external magnetic field is absent,
(b) the external uniform megnetic field B=5.0mT directed perpendicular to the disc. View SolutionQuestion 4
A thin wire AC shaped as a semi-circle of diaameter d=20cm rotates with a constant angular velocity ω=100 rad/s in a unifrom magnetic field of induction B=5.0mT, with ω↑↑B. The rotation axis passes through the end A of the wire and is perpendicular to the diameter AC. Find the value of a line intergal ∫Edr along the wire from point A to C. Generalize the botained result.View SolutionQuestion 5
A wire loop enclosing as semicircle of radius R is located on the boudary of uniform magnetic field B. At the moment t=0, the loop is set into rotation with a costant angular acceleration α about an axis O coinciding with a line of vector B on the boundary. Find the emf induced in the loop as a function of time. Draw the approximate plot of this function.The arrow in the figure shows the emf direction taken to be positive.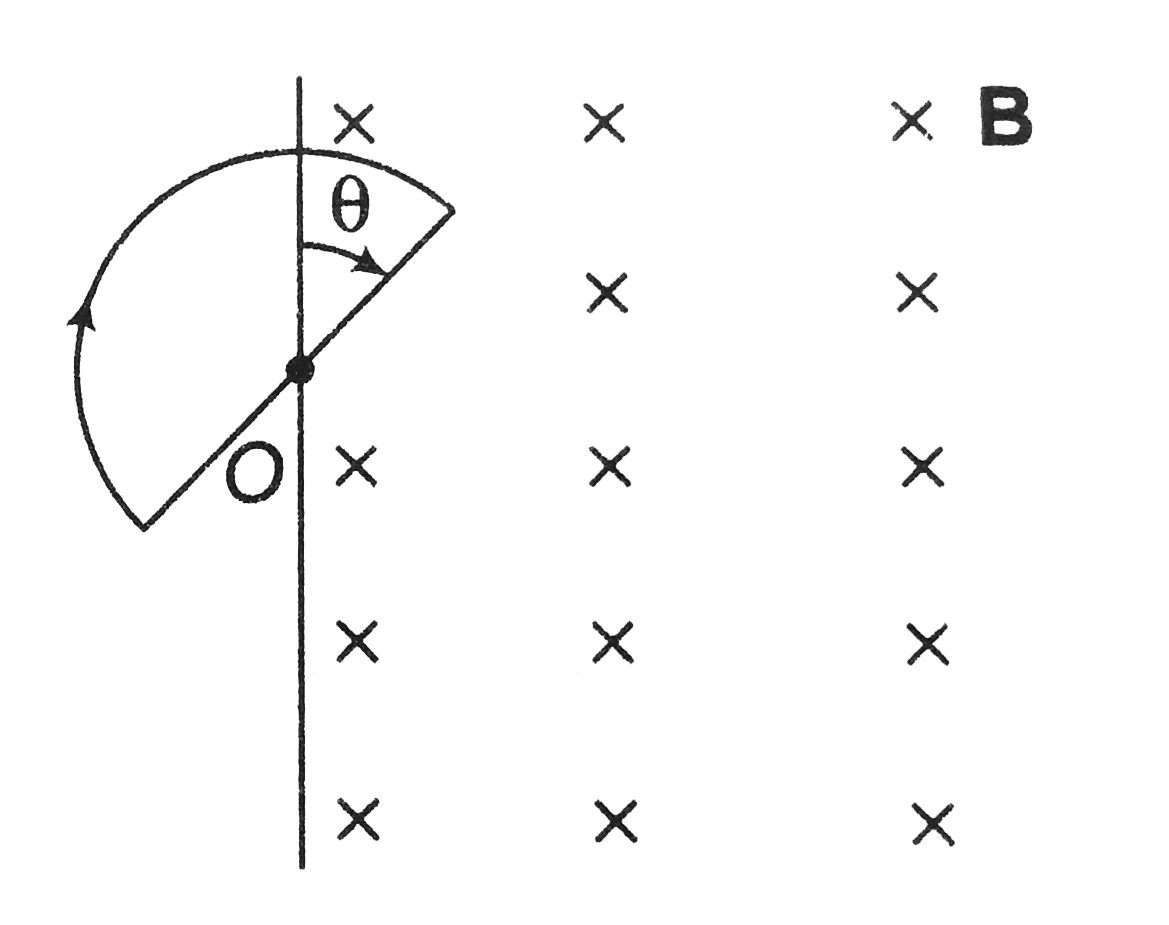 View Solution
View SolutionQuestion 6
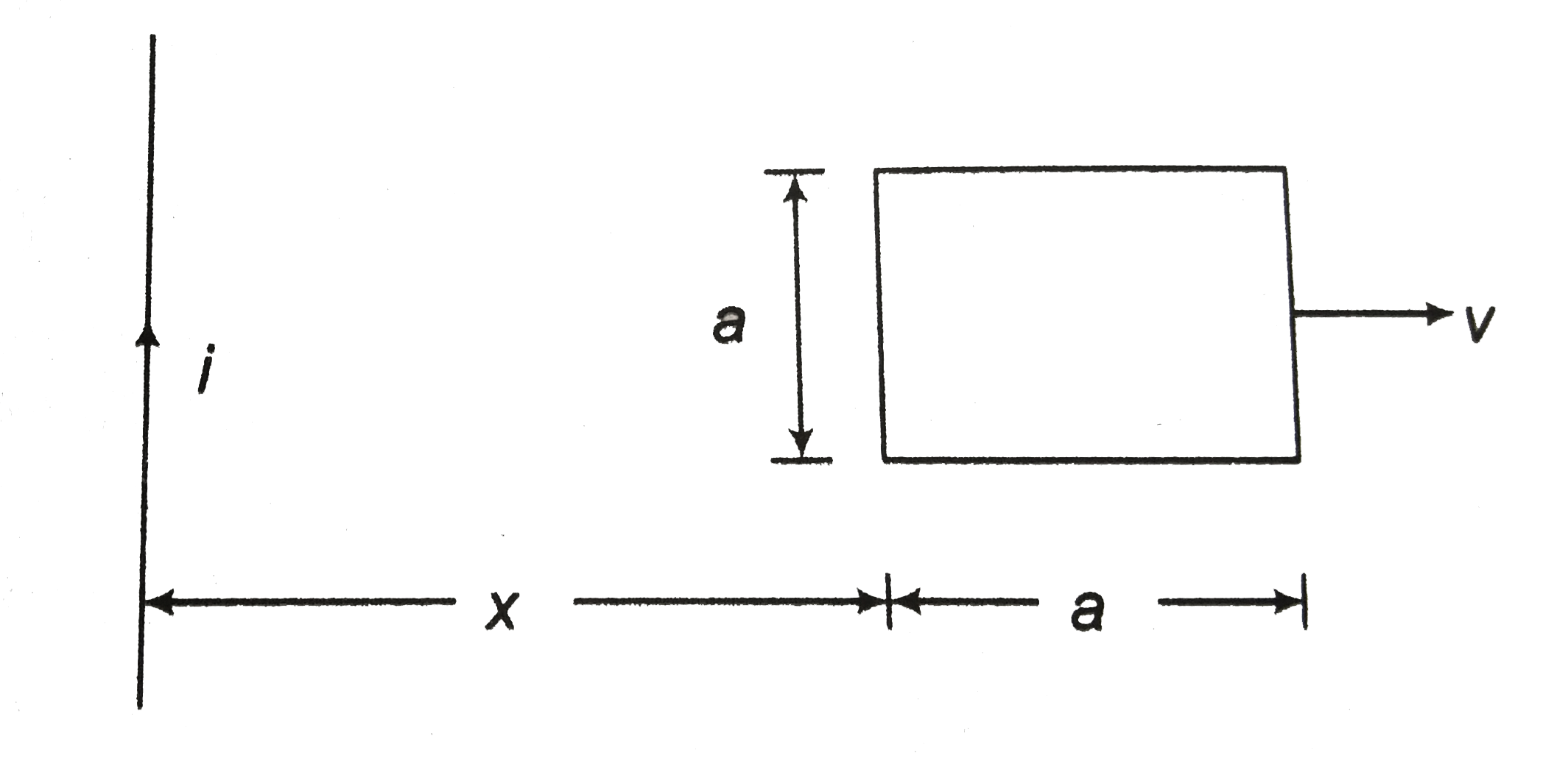
A long straight wire carrying a current I and a II- shaped conductor with siding connector are located in the same plane as shown in Fig. The connector of length l and resistance R sides to the right with a current induced in the loop as a function of separation r between the connector and the stragiht wire. The resistance of the II-shaped conductor and the self-induced of the loop are assumed to be negligible.
 View Solution
View SolutionQuestion 8
A metal rod of mass m can rotate about a horizontal axis O, sliding along a circular conductor of radius a (fig). The arrangment is located in a unifrom magnetic field of induction B directed perpendicular to the ring plane. The axis and the ring are connected to an emf source to form a circuit of resistance R. Neglecting the friction, circuit induction and ring resistance, find the law according to which the source and must very to make the rod rotate with a constant angular velocity ω.
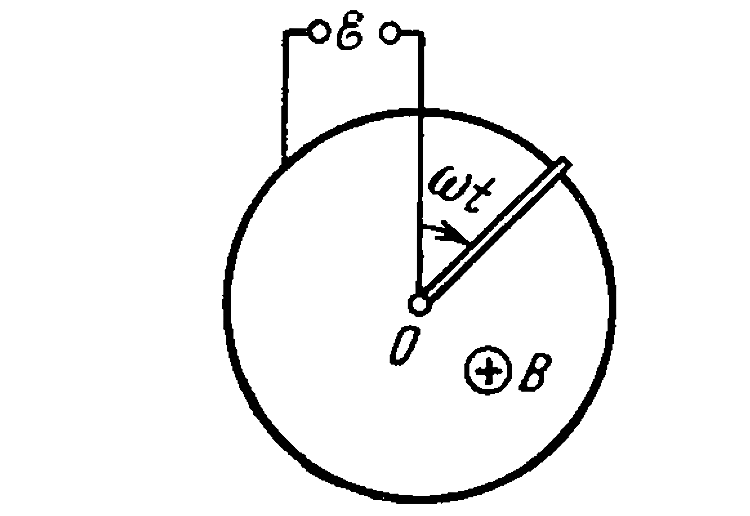 View Solution
View SolutionQuestion 9
A copper connector of mass m slides down two smooth cooper bars, set at an angle α to the horizontal due to gravity (Fig). At the top the bars is equal to l. The system is located in a unifrom magnetic field of induction B, perpendicular to the plane in which the connector slides. The resistances of the bars, the connector and the sliding contacts, as well as the self-inductance of the loop, are assumed to be negligible. Find the steady-state velocity of the connector.
 View Solution
View SolutionQuestion 11
A wire shaped as a semi-circle of radius a rotates about sn sxis OO' with an angular velocity ω in a unifrom magnetic field of induction B' (Fig). The rotation axis is perpendicular to the field direction. The total resistance of the circuit is equal to R. NEglecting the magnetic field of the induced current, find the meand amount of thermal power being generated in the loop fueing a rotation period.
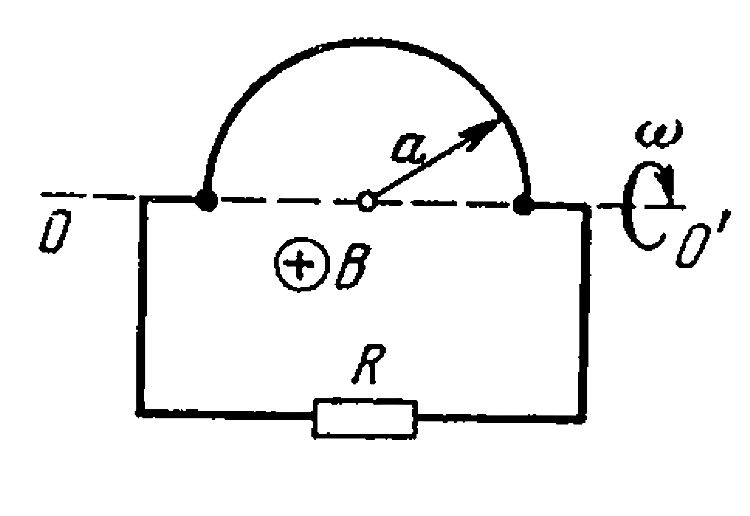 View Solution
View SolutionQuestion 12
A small coll is intorduced between the poles of an electromagnent so that its axis coincides with the magnetic field direction. The cross sectional ara of the coil is equal to S=30mm2, the its diameter a balistic galvanometer connected to the coil indicates a charge q=4.5μC flowing through it. Find the magnetic induction magnitude between the poles provided the total resistance of the electric circuit equals R=40ΩView SolutionQuestion 13
A square wire frame with side a and a straight conductor carrying constant current I are located in the same plane (Fig). The inductance and the resitance of the frame are equal to L and R respectively. The frame was turned throgh 180∘ about the axis OO'separated fromt the current carrying conductor by a distance b. FInd the electric charge having flown through the frame.
 View Solution
View SolutionQuestion 14
A long straight wire carries a current I0. At distances a and b from it there are two other wires, parallel to the former one, which are interconnected by a resistance R (Fig). A connector slides without friction along the wires with a constant velocity v. Assuming the resistances of the wires, the conductor, the sliding contacts, and the self-inductance of the frame to be negligable, find:
(a) the magnitude and the direction of the current induced in the connector,
(b) the force required to maintain the connector's velocity constant.
 View Solution
View SolutionQuestion 15
A conductor rod AB of mass m slides without friction over two long conducting rails separated by a distance (Fig) At the left end the raidls are interconnected by a resistance R. The system is located in a unifrom magnetic fileld perpendicular to the plane of the loop. At the moment t=0 the rod AB starts moving to the right with an initial velocity v0. Neglecting the resistances of the rails and the rod AB, as wellas the self -indcuctance, find:
(a) the distance covered by the rod until it comes to a standsill,
(b) the amount of heat generated in the resitance R during this process.
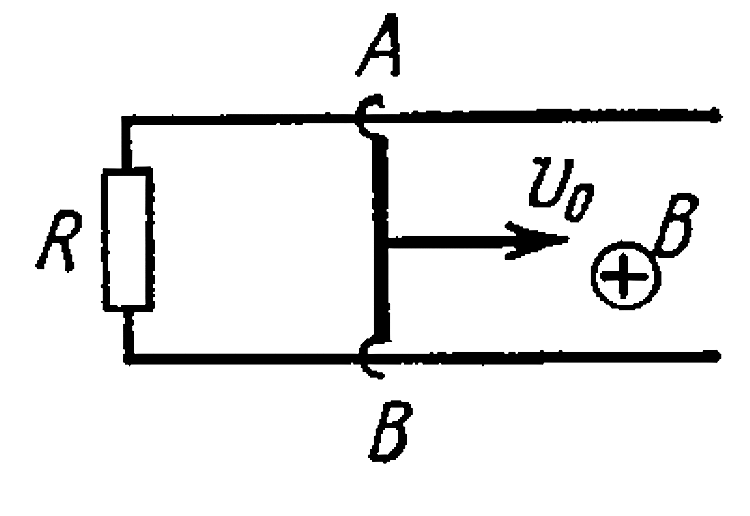 View Solution
View SolutionQuestion 16
A connector AB can slide without frictiion along a II-shaped conductor located in a horizontal plane (Fig). The connector has a length l, mass m and resistance R. The whole system is located in a unifrom magnetic field of induction B directed vertically. At the moment t=0 a constant horizontal force F starts acting on the connector shifting it translationwise to the right. Find how th e velocity o fhte connector varies with time t. The inductance of the loop and the resistance of the II-shaped conductor conductor are assumed to be negligible
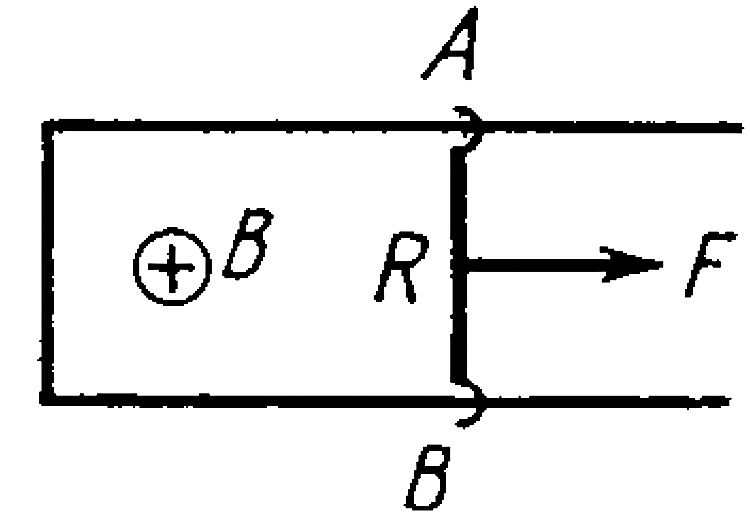 View Solution
View SolutionQuestion 18
A plane loop is shaped as two squares (Fig) and placed in a uniform magnetic field at right angle to the loop's plane. The magnetic induction varies with time as B=B0sin(ω)t,whereB0=10mTand(ω)=100rads−1. The wires do not touch at point A. If resistance per unit length of the loop is 50m(Ω)/m, then amplitude of current induced in the loop is
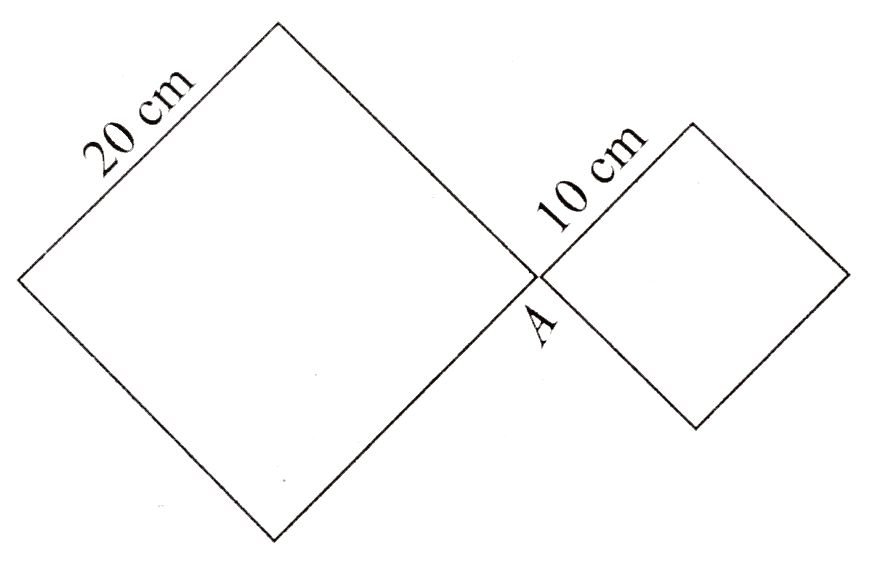 View Solution
View SolutionQuestion 19
A plane loop is shaped as two squares (Fig) and placed in a uniform magnetic field at right angle to the loop's plane. The magnetic induction varies with time as B=B0sin(ω)t,whereB0=10mTand(ω)=100rads−1. The wires do not touch at point A. If resistance per unit length of the loop is 50m(Ω)/m, then amplitude of current induced in the loop is
 View Solution
View SolutionQuestion 20
A π shaped metal frame is located in a uniform magnetic field perpendicular to the plane of the conductor and varying with time at the rate (dB/dt)=0.I0T/sec . A conducting connector starts moving with an acceleration a=I0cm/sec2 along the parallel bars of the frame. The lenght o0f the connector is equal to l=20cm . Find the emf induced in the loop t=2sec after the beginnig of the motion, if at the moment t=0 the loop area and the magnetic induction are equal to zero. The inductance of the loop is to be neglected. View SolutionQuestion 21
In a long staright solenoid with cross-sectional radius a and number of turns per unit length n a current varies with a constant velocity.IA/s. Find the magntidue of the eddy current field strength as a function of the distance r from the solenoid axis. Draw the appoximate plot of this function.View SolutionQuestion 22
A long straight solenoid of cross-sectional diameter d=5cm and with n=20 turns per one cm of its length has a round turn of copper wire of cross-sectional area S=1.0mm2 tightly put on its winding. Find the current flowing in the turn if the current in the solenoid winding is increased with a constant velocity .I=100A/s. The inductance of the turn is to be neglected.View SolutionQuestion 23
A long solenoid of cross-sectional radius a has a thin insulates wiere ring tightly put on its winding, one half of the ring has the resistance η times that of the other half. The magneticv induction produced by the solenoid varies with the time as B=bt, where b is a constant. Find the magnitude of the electric field strength in the ring.View SolutionQuestion 24
A thin non-conducting ring of mass m carrying a charge q can freely rotate about its axis. At the initial moment the ring was at rest and no magnetic field was present. Then a practically unifrom magnetic field was switched on, which was perpendicular to the planeof the ring and increased with time according to a certain law B(t), Find the angluar velocity ω of the ring as a function of the induction B(t).View SolutionQuestion 25
A thin wire ring of radius a and resitance r is located inside a long solenoid is equal to l, its cross-sectional radius , to b. At a certain moment the solenoid was connected to a source of a constant voltage V. The total resistance of the circuit is equal to R. Assuming the the radial force acting per unit length of the ring.View SolutionQuestion 27
In the middle of a long solenoid there is a coaxial ring of square cross-seciton, made of conducting materaial with respectivity are equal to h its inside and outside radii are equal to a and b respectively. Find the current induced in the ring if the magnetic induction produced by the solenoid varies with time as B=βt, where βt, where β is constant. THe inductance of the ring is to be neglected.View SolutionQuestion 36
A supercondutig round ring of radius a and inductance L was located in a unifrom magnetic fied of induction B. The ring plane was parallel to the vector B, and the current in the ring was equal to zero. Them the ring was turned through 90∘ so that its plane became perpendicular to the feild. FInd:
(a) the current induced in the ring after the turn,
(b) the work perfromed during the turn.View SolutionQuestion 38
A ring radius a=50mm made of thin wire of radius b=1.0mm was located in a unifrom magnetic field with induction B=0.50mT so that the ring place was perpenficular to the vector B. Then the ring was cooled down to superconducting state, and the magnetic field was swichted off. Find the ring current after that. Note that the inductiance of a thin ring along which the surface current flows is equal to L=μ0a(In8ab−2).View SolutionQuestion 39
A closed circuit consits of a source of constant and E and a choke coil of inductance L connected in series. The active resistance of the whole circuit is equal to R. At the moment t=0 the choke coil inductance was decreased abrupty η times. FInd the current in the circuit as a function of time t.View SolutionQuestion 43
Determine the mutual inductance of a doughnut coil and an infinite straight wire passing along its axis. The coil has recatangular cross-section, its inside radius is equal to a and the outside one, to b. The length of the doughtnut's cross-sectinla side parallel to the wire is equal to h. The coil has N turns. The system is located in a unifrom magnetic with permeability μ.View SolutionQuestion 45
A small cylindrical magnet M (Fig) is placed in the centre of a thin coil of radius a consisting of N turns. The coil in connected to a ballistic galvanometer. The active resistance of the whole circuit is equal to R. Find the magnetic moment of the magnet if its removel from the coil results in a charge q flowing through the galvanometer.
 View Solution
View SolutionQuestion 48
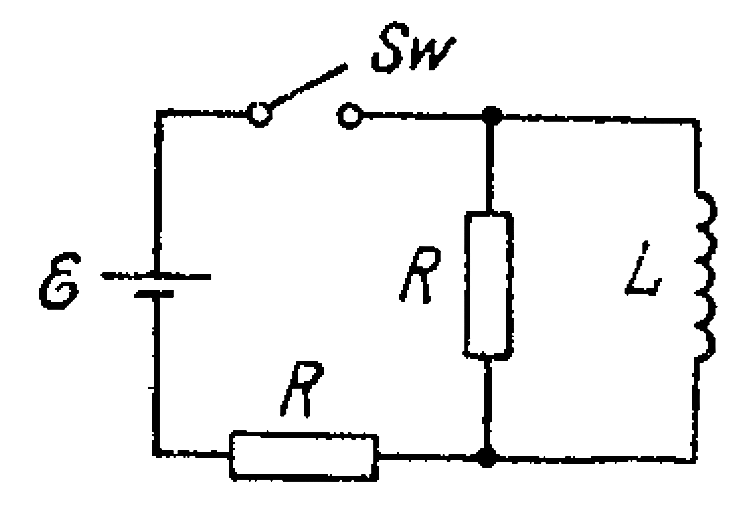
A coil of inductance L=2.0μH and resitance R=1.0Ω is connected to a source of constant emfE=3.0V. A resistance Rs=2.0Ω is connected in parallel with the coil. Find the amount of heat generated in the coil after the swich Sw is disconnecied. The internal resistance of the source is negligible.
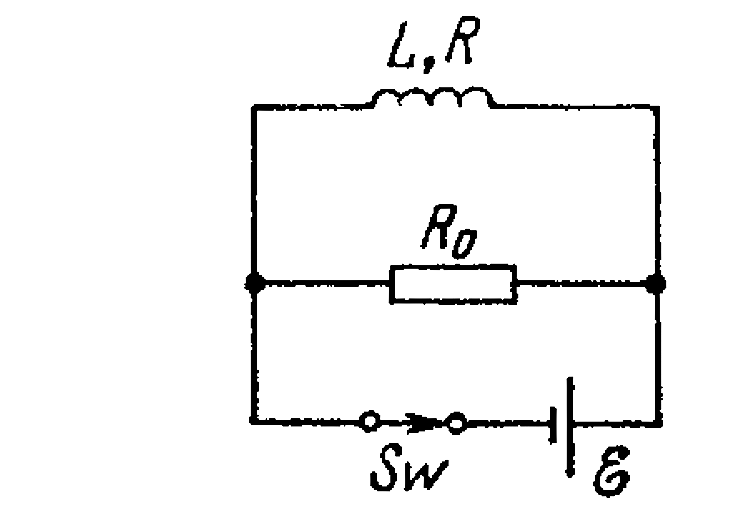 View Solution
View SolutionQuestion 50
An iron core shaped as a doughnut with round cross-section of radius a=3.0cm carreis a winding of N=1000 turns through which a current I=1.0A flows. The mean radius of the doughnut is b=32cm. Using the polt in Fig. Find the magnetic energy strored up in the core. A field strength H is suposed to be the same throughout the cross-section and equal to its magnitude in the centre of the cross-section.View SolutionQuestion 51
A thin ring made of magnetic has a mean diameter d=30cm and supports a winding of N=800 turns. The cross-sectional area of the ring is equal to S=5.0cm2. The ring has a cross-cut of width b=2.0mm. When the winding carries a certain current, the permeability of the magnectic equals μ=1400. Neglectign the disipation of magnetic flux at the gap edges, find:
(a) the ratio of magnetic energies in the gap and in the magnetic,
the inductance of the system, do it two ways: using the flux and using the energy of the field.View SolutionQuestion 58
Demonstarate that the magnetic energy of interaction of two current-carrying loops located in vacumm can be represented as Wia=(1μ0)∫B1B2dV, where B1 and B2 are the magnetic inductions within a volume element dV, produced indiviually by the currents of the first and the secound loop respectively.View SolutionQuestion 60
The space between two concentric metallic spheres is filled up with a unifrom poorly conducting medium of resistivity ρ and permittivity ε. At what moment t=0 the inside sphere obtains a certain charge. Find:
(a) the relation between the vectros of displacement current density and conduction current density at an arbitarry point of the medium at the same moment of time,
(b) the displacement current across an arbitrary closed surface wholly located in the medium and enclosing the internal sphere, if at the given moment of time the charge of that sphere is equal to q.View SolutionQuestion 62
A parallel plate air condenser whose each plate has an area S=100cm2 is connected in series to an ac circuit. Find the electric field strength amplitude in the capacitor if the sinusolidal current amplitude in lead wires is equal to Im=1.0mA and the current frequency equals ω=1.6.107S−1.View SolutionQuestion 63
The space between the electrodes of a parallel-plate capacitor is filled with a uniform poorly conducting medium of conductivity σ and permittivity ε. The capacitor plates shaped as round discs are separted by a distance d. Neglecting the edge effects, find the magnetic field strength between the plates at a distance r from their axis if an ac voltage V=Vmcosωt is applied to the capacitor.View SolutionQuestion 66
A thin wire ring of radius a carrying a charge q approcahes the observation point P so that its centre moves rectilinearly with a constant velocity v. The plane of the ring remians perpendicular to the motion direction. At what distance xm from the point P will the ring be located at the moment when the displacement current density at the point P becomes maximum? What is the magnitude of this maximum density ?View SolutionQuestion 68
Using Maxwell's equacations. Show that
(a) a time dependent magnetic field cannot exist without an electric field,
(b) a unifrom electric field cannot exist in the presence of a time-dependence magnetic field,
(c) inside an empty cavity a unifrom electric (or magnetic ) field can be time-dependent.View SolutionQuestion 72
In the interial reference frame K there is a unifrom magentic field the induction B. Find the electric feidl strength in the frame K' which moves relative to the frame K with a non-relatistic veclocity v, with v⊥B. To solve this problem, consider the forces acting an an imaginary charge in the frame K' is equal to zero.View SolutionQuestion 77
In an interial reference frame K there is only magnetic field with induction B=b(yl−x)/(x2+y2), where b is a constane, i and j are the unit vectors of the x and y axes. Find the elecric field strength E' in the frame K' moving relative to the frame K with a constatn non-relative velocity v=vk,k is the unit vector of the z-axis. The z' axis is assumed to coincule with the z axis. What is the shape of the field E' ?View SolutionQuestion 78
In an interial reference from K there is only electric field of strength E=a(xl+y)/x2+y2), where a is a constant, i find j are unit vectors of the x and y axes. Find the magtnetic induction B' in the frame K' moving relative to the freame K with a consant non-relativistic velocity v=vklk is the unit vector of the z-axis. The z' axis is assumed to coincule with the z-axis. What is the shape of the magnetic induction B' ?View SolutionQuestion 80
In an inertial reference frame K there is only a unifrom electric field E=8kV/m in strength. Find the modulus and direction
(a) of the vector E' (b) of the vector B' in the interial refrernce frame K' moving with a constant velocity v relative to the frame K at an angle α=45∘ to the vector E. The velocity of the frame K' is equla to aβ=0.60 fraction of the velocity of light.View SolutionQuestion 83
In an interial reference frame K there are two uniform mutulaly perpendicular fields, an electric field of strength E=40kV/m and a magnetic fleid induction B=0.20mT. Find the electric strength E' (or the magnetic induction B') in the reference frame K' where only one field, electric or magnetic, is observed. View SolutionQuestion 84
A point charge q moves unifromly and rectilnearly with a relativistic with a relativistic velocity of light (β=v/c). Find the electric field strength E produced by the charge at the point whose radius vector relatives to the charge is equal to r and forms an angle θ with its velocity vector.View Solution