चतुर्भुज कक्षा 9 गणित
भूमिका
अध्याय के शीर्षक के अनुसार इस अध्याय मे हम चतुर्भुज का अध्ययन करेंगे। आपने पिछली कक्षा 8 में चतुर्भुजों के बारे मे पढ़ा हैं, चतुर्भुज एक समतल आकृति होती है जिसकी चार भुजाएँ या चार किनारे होते हैं और चार कोने भी होते हैं। चतुर्भुज आम तौर पर चार भुजाओं जैसे आयत, वर्ग, समलम्बाकार, और पतंग जैसे आकार के होते हैं। इस अध्याय मे हम चतुर्भुज का कोण योग गुण, चतुर्भुज के प्रकार, समान्तर चतुर्भुज के गुण, चतुर्भुज के समांतर होने के लिए प्रतिबंध, मध्य बिंदु प्रमेय का अध्ययन करेंगे।
आइये जानते है, चतुर्भुज को और करीब से ...
बच्चो आप अध्याय 6 और अध्याय 7 में त्रिभुजों के अनेक गुणों के बारे में अध्ययन कर चुके हैं। आप यह भी जानते हैं कि तीन असंरेख बिंदुओं को युग्मों में जोड़ने पर जो आकृति प्राप्त होती है,त्रिभुज कहलाती है। अब, आइए चार बिंदु अंकित करें और देखें कि क्रमानुसार युग्मों में इनको जोड़ने पर क्या आकृति प्राप्त होती है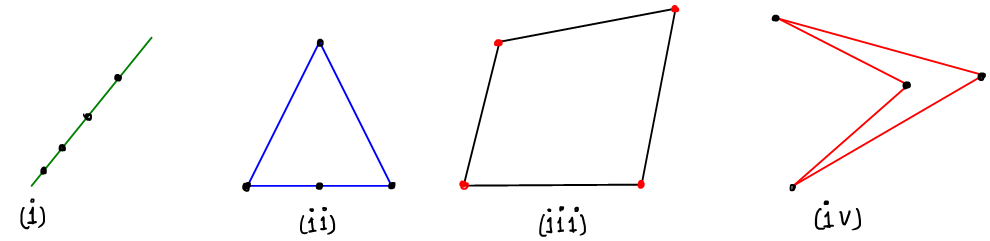
ध्यान दीजिए कि यदि सभी बिंदु संरेख हों (एक ही रेखा में हों), तो हमें एक रेखाखंड प्राप्त होता है। [ आकृति (i )]
यदि चार बिंदुओं में से तीन संरेख हों, तो हमें एक त्रिभुज प्राप्त होता है। [आकृति (ii)]
और अब बात करते हैं चतुर्भुज की | यदि चार में से कोई तीन बिंदु संरेख न हों, तो हमें चार भुजाओं वाली एक आकृति प्राप्त होती है। [ आकृति (iii) और (iv)]
चारों बिन्दुओं को एक क्रम में जोड़ने से इस प्रकार प्राप्त आकृति चतुर्भुज (quadrilateral) कहलाती है। इस अध्याय में हम केवल आकृति (iii) में दिए गए जैसे चतुर्भुजों का ही अध्ययन करेंगे , आकृति (iv) में दिए गए जैसे चतुर्भुजों का नहीं।एक चतुर्भुज की चार भुजाएँ, चार कोण और चार शीर्ष होते हैं। [ आकृति ]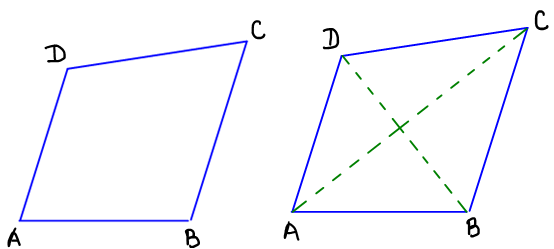
चतुर्भुज ABCD में,AB,BC,CD औरDA चार भुजाएँ (sides) हैं;A,B,C और D चार शीर्ष (Vertices) हैं तथा ∠A, ∠B, ∠C और ∠D शीर्षों पर बने चार कोण (angle) हैं
अब सम्मुख शीर्षों A और C तथा B और D को जोड़िए [ उपर्युक्त आकृति ]।AC औरBD चतुर्भुजABCD के दो विकर्ण (diagonals)कहलाते हैं।
इस अध्याय में, हम विभिन्न प्रकार के चतुर्भुजों और उनके गुणों के बारे में अध्ययन करेंगे। विशेष तौर पर हम समांतर चतुर्भुजों के बारे में पढ़ेंगे।
बच्चों ज़रा ध्यान दो
आप सोच सकते हैं कि हम चतुर्भुजों (या समांतर चतुर्भुजों) का ही क्यों अध्ययन करें। अपने चारों तरफ देखेंगें तो पायेंगें की आपके आस-पास चतुर्भुज के आकार की अनेक वस्तुएँ हैं, जैसे- आपकी कक्षा का फर्श, दीवार, छत, खिड़कियाँ, श्यामपट्ट, डस्टर (duster) का प्रत्येक फलक आपकी पुस्तक का प्रत्येक पृष्ठ, पढ़ने की मेज का ऊपरी पृष्ठ, इत्यादि। इनमें से कुछ को नीचे दिखाया गया है (देखिए आकृति)-
जबकि हमारे आस-पास दिखने वाली अधिकांश वस्तुएँ आयत के आकार की हैं, फिर भी हम चतुर्भुजों और विशेषकर समांतर चतुर्भुजों के बारे में और अधिक अध्ययन करेंगे, क्योंकि एक आयत एक समांतर चतुर्भुज ही है और समांतर चतुर्भुज के सभी गुण आयत के लिए भी सत्य होते हैं।
चतुर्भुज का कोण योग गुण
एक चतुर्भुज के चारों अंत: कोणों का योग 360∘ होता है। आइए इससे सम्बन्धित प्रमेय देखते है -
हम इसकी जाँच चतुर्भुज का एक विकर्ण खींच कर उसे दो त्रिभुजों में विभाजित करके कर सकते हैं।
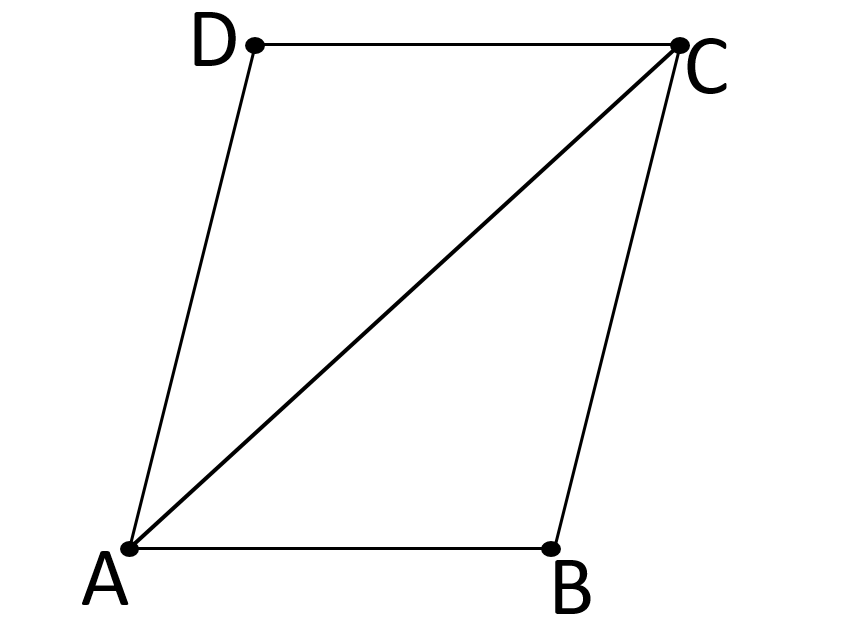
मान लीजिए ABCD एक चतुर्भुज है और AC उसका एक विकर्ण है
अतः दो त्रिभुज प्राप्त होंगे △ADC और △ABC
हम जानते हैं कि त्रिभुज के तीनों कोणों का योग 180∘ होता है।
अतः △ADC में ,
∠DAC+∠ACD+∠D =180∘..........(1)
इसी प्रकार, △ABC में,
∠CAB+∠ACB+∠B =180∘..........(2)
समीकरण (1) और (2) को जोड़ने पर,
∠DAC+∠ACD+∠D+∠CAB+∠ACB+∠B =180∘ + 180∘
∠DAC+∠ACD+∠D+∠CAB+∠ACB+∠B =360∘
चूँकि ∠DAC+∠CAB=∠A और ∠ACD+∠ACB=∠C
अतः ∠A+∠B+∠C+∠D=360∘ है।
अर्थात् चतुर्भुज के चारों कोणों का योग 360° होता है।
उदाहरण 1
एक चतुर्भुज के कोण 1:4:2:3 के अनुपात मे हो तो कोणों के मान ज्ञात कीजिए
माना चतुर्भुज के चार कोण x,4x,2x व 3x है।
हम जानते है की चतुर्भुज के चारों कोणों का योग 360∘ होता है ।
∴x+4x+2x+3x=360∘
⇒10x=360∘
⇒x=36∘
इसलिए चतुर्भुज के चारों कोण निम्न प्रकार है-
x=36∘
4x=4×36∘=144∘
2x=2×36∘=72∘
3x=3×36∘=108∘
चतुर्भुज के प्रकार
चतुर्भुज के प्रकारों को समझने के लिए हम निम्नांकित चित्र को ध्यान से देखते हैं -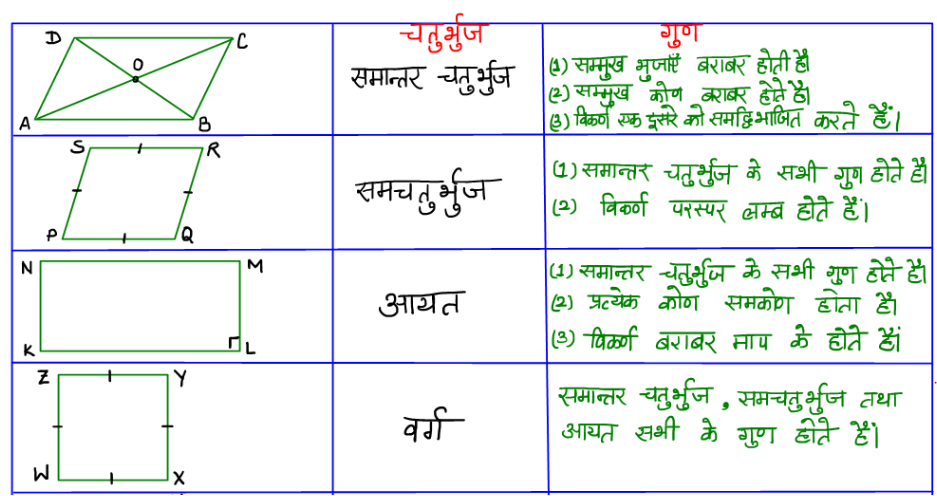
समान्तर चतुर्भुज के गुण
अभी हम समांतर चतुर्भुज के बारे में पढ़ चुके है अब हम समांतर चतुर्भुज के गुणों के बारे में पढेंगें | इसके लिए हम कुछ प्रमेय का अध्ययन करते है जो की निम्नलिखित हैं -
प्रमेय 1
किसी समांतर चतुर्भुज का एक विकर्ण उसे दो सर्वांगसम त्रिभुजों में बांटता है।
मान लीजिए ABCD एक समांतर चतुर्भुज है और AC उसका एक विकर्ण है।

चित्र मे विकर्ण AC समांतर चतुर्भुज ABCD को दो त्रिभुजों ABC और CDA में विभाजित करता है।
हमें सिद्ध करना है कि ये दोनों त्रिभुज सर्वांगसम हैं। (△ABC≅△CDA)
△ABC और △CDA के लिए ध्यान दीजिए कि BC || AD है और AC एक तिर्यक रेखा है।
इसलिए, ∠BCA=∠DAC (एकांतर कोण)
साथ ही, AB || DC और AC एक तिर्यक रेखा है।
इसलिए, ∠BAC=∠DCA (एकांतर कोण)
और AC = CA ( उभयनिष्ठ भुजा )
अतः, △ABC≅△CDA
[ ASA सर्वांगसमता से ]
अर्थात् विकर्ण AC समांतर चतुर्भुज ABCD को दो सर्वांगसम त्रिभुजों ABC और CDA में विभाजित करता हैं।
प्रमेय 2
एक समांतर चतुर्भुज में सम्मुख भुजाएँ बराबर होती है।
आप पहले ही सिद्ध कर चुके हैं कि समांतर चतुर्भुज का विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभाजित करता है।
अतः हम कह सकते हैं की समांतर चतुर्भुज कि सम्मुख भुजाएँ बराबर होंगी ।
इसलिए, AB = DC और AD = BC है।
मान लीजिए ABCD एक समांतर चतुर्भुज है और AC उसका एक विकर्ण है।
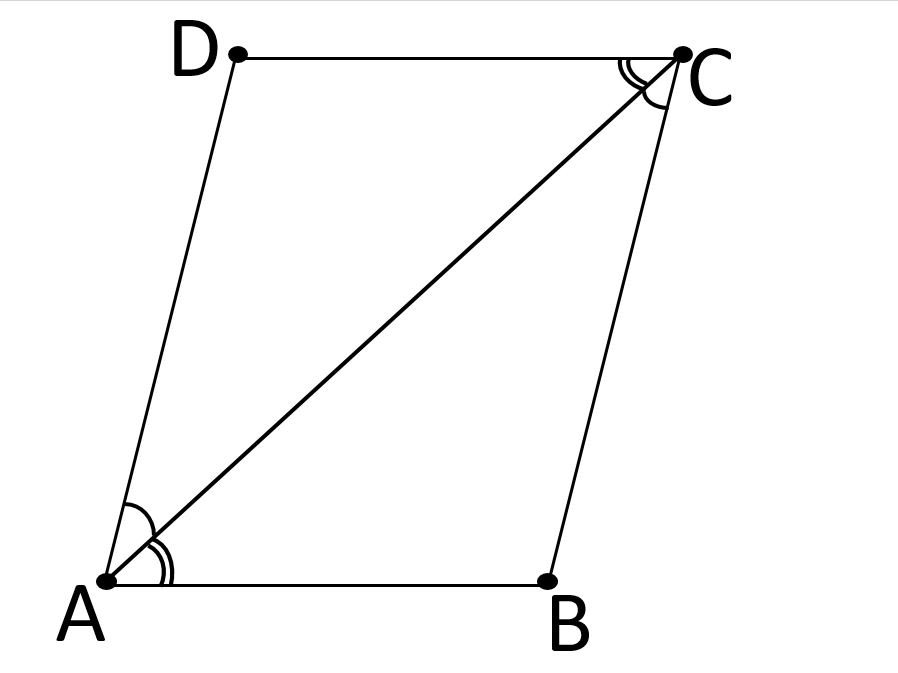
देखिए कि विकर्ण AC समांतर चतुर्भुज ABCD को दो त्रिभुजों ABC और CDA में विभाजित करता है।
हमें सिद्ध करना है कि AB = DC और AD = BC (△ABC≅△CDA)
△ABC और △CDA के लिए ध्यान दीजिए कि BC || AD है और AC एक तिर्यक रेखा है।
इसलिए, ∠BCA=∠DAC (एकांतर कोण)
साथ ही, AB || DC और AC एक तिर्यक रेखा है।
इसलिए, ∠BAC=∠DCA (एकांतर कोण)
और AC = CA ( उभयनिष्ठ भुजा )
अतः, △ABC≅△CDA होगा |
अर्थात् विकर्ण AC समांतर चतुर्भुज ABCD को दो सर्वांगसम त्रिभुजों ABC और CDA में विभाजित करता हैं
AB = DC और AD = BC होगा। [ CPCT से ]
अतः एक समांतर चतुर्भुज में सम्मुख भुजाएँ बराबर होती है।
उदाहरण 2
दर्शाइए कि यदि एक चतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करें, तो वह एक समचतुर्भुज होता है।
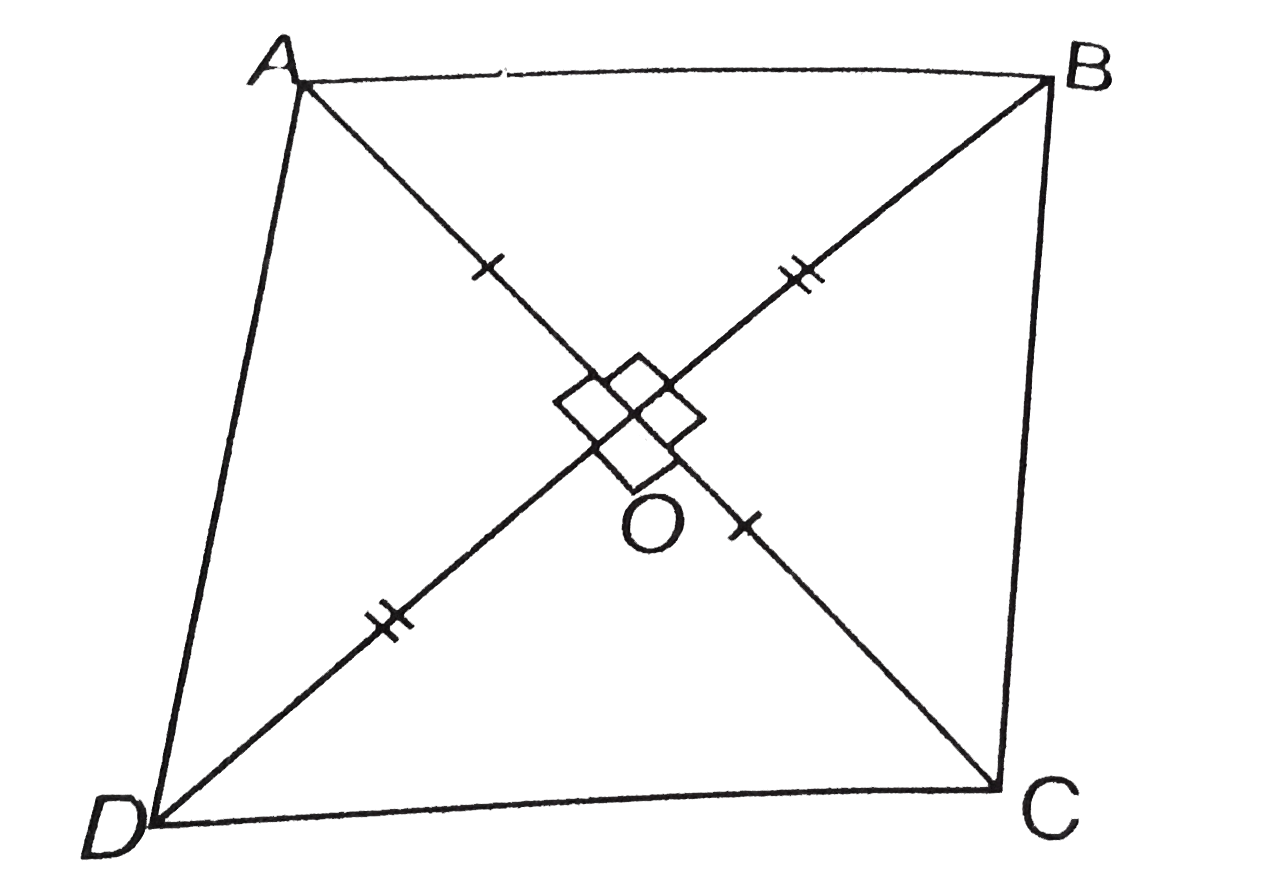
एक चतुर्भुज ABCD जिसके विकर्ण AC और BD एक –दूसरे को समकोण पर समद्विभाजित करते हैं
अर्थातOA=OC
औरOB=OD
और
∠AOD=∠AOB=∠COD=∠BOC=90∘
दर्शाना है:
ABCD एक समचतुर्भुज है।
उपपति
ΔOAB और ΔODC में
∵⎧⎪⎨⎪⎩OA=OCOB=OD∠AOB=∠COD (दिया है)
∴ΔOAB≅ΔOCD (S.A.S. से)
∴AB=CD (c.p.c.t)…….(1)
पुन: ΔOAD और ΔOBC में
∵⎧⎪⎨⎪⎩OA=OCOD=OB∠AOD=∠BOC (दिया है)
∴ΔOAD≅ΔOCB (S.A.S. से )
∴AD=BC(c.p.c.t.)……….(2)
इसी प्रकार सिद्ध कर सकते हैं कि
AB=AD
CD=BC………………(3)
अतः 1,2 और 3 से
AB=BC=AD=CD
अतः ABCD एक समचतुर्भुज है।
उदाहरण 3
ABCD एक आयत है जिसमें विकर्ण AC, कोण A और C दोनों को समद्विभाजित करता है। सिद्ध कीजिए कि:
(i) ABCD एक वर्ग है।
(ii) विकर्ण BD, कोण B और D को समद्विभाजित करता है।
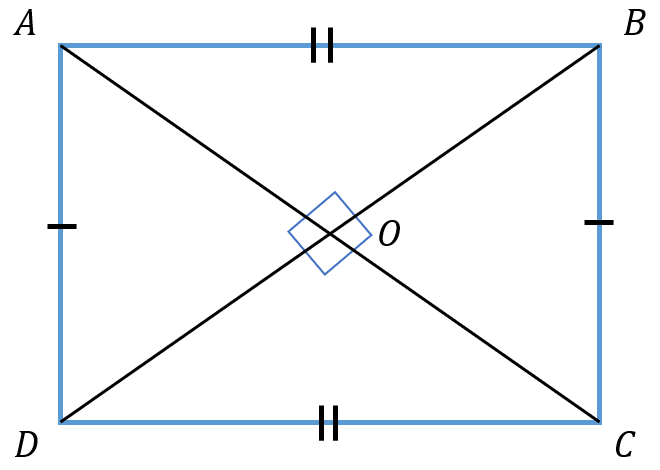
दिया है:
ABCD एक आयत है।
∴AB=CD और BC=AD…………..1
सिद्ध करना है:
(i) ABCD एक वर्ग है।
अर्थात
AB=BC=CD=DA
(ii) विकर्ण BD,∠B और ∠D दोनों को समद्विभाजित करता है।
उपपति:
(i) ΔADC और ΔABC में
AB∣∣DC और तिर्यक रेखा AC इनको काटती है।
∵⎧⎪⎨⎪⎩∠DAC=∠BAC∠DCA=∠BCAAC=CA (दिया है )
∴ΔADC≅ΔABC (A.S.A. से )
∴AD=AB (c.p.c.t)
और CD=BC…………2
अतः समीकरण 1 और 2 से
AB=BC=AD=CD
∴ABCD एक वर्ग है।
(ii) ΔAOB और ΔCOB में
AB=BC
(एक वर्ग की भुजाएं)
BO=OB
उभयनिष्ठ
OA=OC
( वर्ग के विकर्ण एक-दूसरे को समद्विभाजित करते हैं)
∴ΔAOB≅ΔCOB
(S.S.S. से )
∴∠OBA=∠OBC
(c.p.c.t)
अतः BO या BD,∠B को समद्विभाजित करती है।
इसी प्रकार ΔAOD और ΔCOD में
AD=CD
(वर्ग की भुजाएं)
OD=DO
(उभयनिष्ठ)
OA=OC
( ∵ वर्ग के विकर्ण एक-दूसरे की समद्विभाजित करते है।)
∴ΔAOD≅ΔCOD
(S.S.S से)
∴∠ADO=∠CDO
अतः DO या DB,∠D को समद्विभाजित करती है।
उदाहरण 4
दो रेखाखण्ड AC व BD बिन्दु P पर समद्विभाजित करते है। सिद्ध कीजिए की ABCD एक समान्तर चतुर्भुज है।
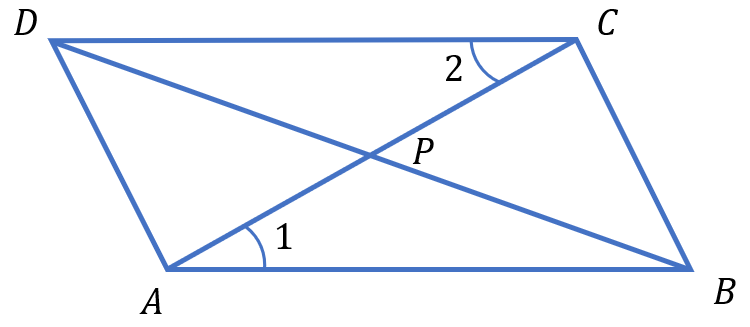
ΔAPB व ΔCPD में
AP=CP [ दिया है ]
BP=DP [दिया है ]
व ∠APB=∠CPD [ शीर्षाभिमुख कोण ]
ΔAPB≅ΔCPD [ SASसर्वांगसमता से ]
⇒AB=CD
[CPCT].....(1)
व ∠1=∠2
लेकिन ∠1 व ∠2 एकान्तर कोण के युग्म है
∴AB||DC ...(2)
अतः समीकरण (1) व (2) से ABCD एक समान्तर चतुर्भुज है।
प्रमेय 3
यदि एक चतुर्भुज की सम्मुख भुजाओं का प्रत्येक युग्म बराबर हो तो वह चतुर्भुज समांतर चतुर्भुज कहलाता है।
मान लीजिए ABCD एक समांतर चतुर्भुज है और AC उसका एक विकर्ण है। एवं उनकी सम्मुख भुजायें बराबर हैं |
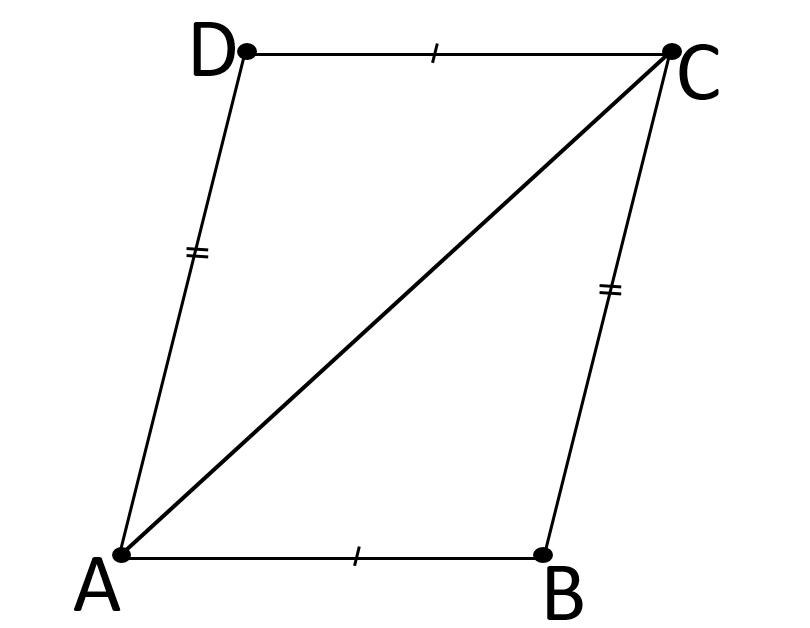
अतः △ABC तथा △CDA
इसलिए , AB = CD , BC = AD तथा उभयनिष्ठ भुजा AC = AC
स्पष्ट है कि ,
△ABC≅△CDA
[SSS सर्वांगसमता से ]
अतः ∠BAC=∠DCA और ∠BCA=∠DAC
[CPCT से ]
दोनों कोण एकांतर कोणों के युग्म हैं |
इसलिए ∠B=∠D
अतः AB||CD तथा BC||AD
इसलिए, ABCD एक समांतर चतुर्भुज है |
उदाहरण 5
ΔABC और ΔDEF में AB=DE,AB||DE,BC=EF और BC||EF है। शीर्षों A,B,C को क्रमशः शीर्षों D,E,F से जोड़ा जाता है। दर्शाइए कि
(i) चतुर्भुज ABED एक समांतर चतुर्भुज है।
(ii) चतुर्भुज BEFC एक समांतर चतुर्भुज है।
(iii) AD∣∣CF और AD=CF है।
(iv) AC=DF है।
(v) चतुर्भुज ACFD एक समांतर चतुर्भुज है।
(vi) ΔABC≅ΔDEF है।
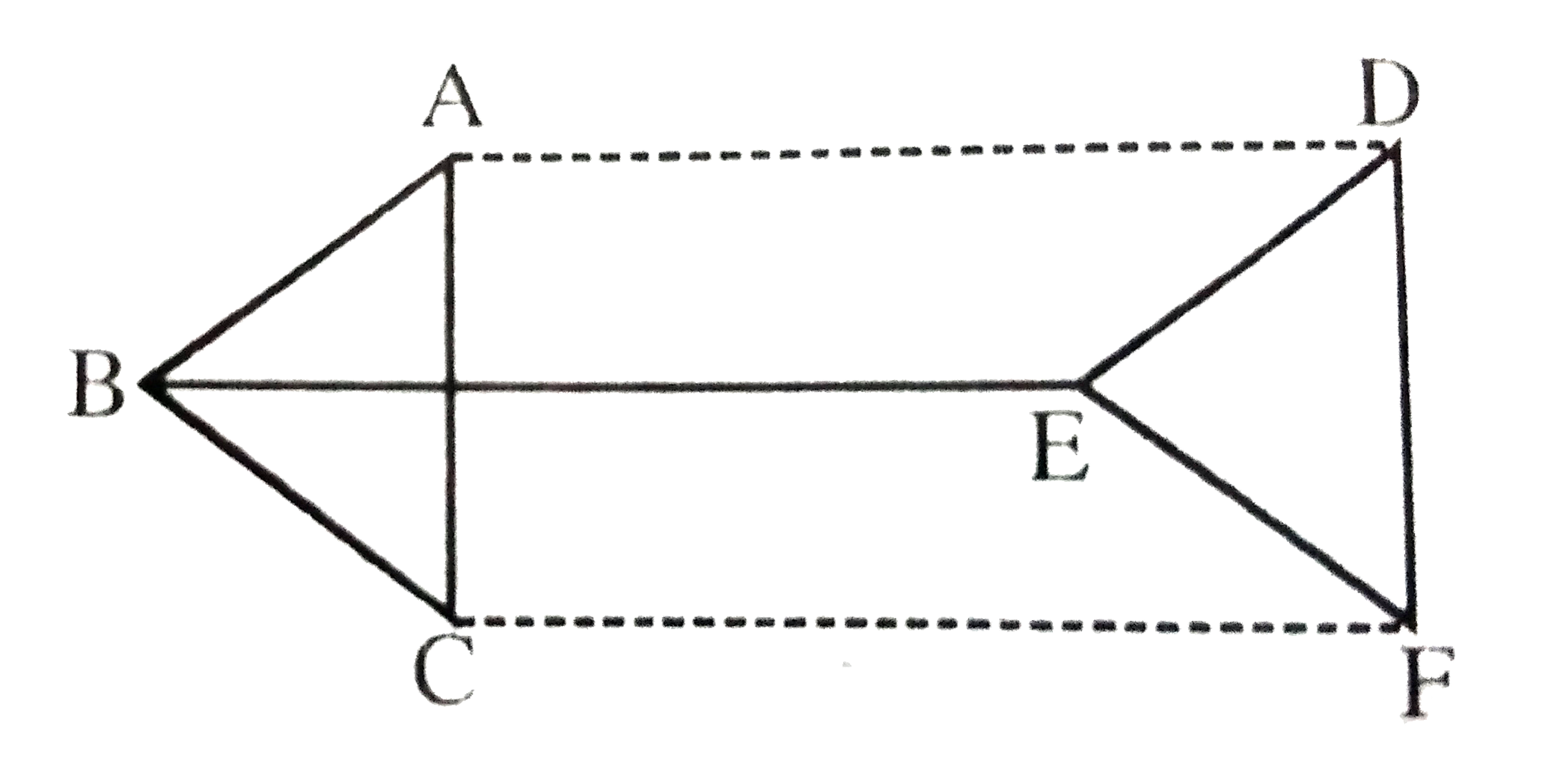
(i) दिया है :
AB||DE तथा
AB=DE
AD||BE
तथा AD=BE
∴ अतः ABED एक समांतर चतुर्भुज है।
(ii) BE||CF
तथा BE=CF
BC||EF
तथा BC=EF
∴ अतः BEFC एक समांतर चतुर्भुज है।
(iii)
(i) और (ii) से
AD||CF
तथा AD=CF
(iv)
(iii) में हम सिद्ध कर चुके है, कि
AC||DF
तथा AC=DF
(v) AC||DF
तथा AC=DF
AD||CF
तथा AD=CF
अतः ACFD एक समांतर चतुर्भुज है।
(vi) अब ΔABC तथा ΔDEF में
AC=DF
[ चूंकि ACFD एक समांतर चतुर्भुज है]
AB=DE
[ चूंकि ABED एक समांतर चतुर्भुज है]
तथा BC=EF
[ चूंकि BCFE एक समांतर चतुर्भुज है]
अतः ΔABC≅ΔDEF
[SSS सर्वांगसमता नियम से]
प्रमेय 4
एक समांतर चतुर्भुज में सम्मुख कोण बराबर होते हैं।
माना कि ABCD एक समांतर चतुर्भुज है।
अत: DC || AB और AD || BC
[चूँकि समांतर चतुर्भुज में सम्मुख भुजाएँ समांतर होती हैं।]
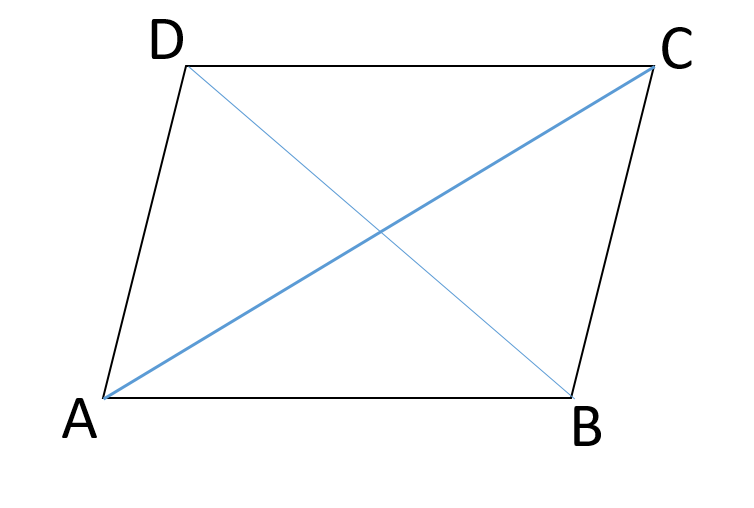
सिद्ध करना है -
∠ABC=∠CDA और, ∠DAB=∠BCD
बिंदु A और C तथा बिंदु D और B को मिलाया गया।
अतः △ACD और △ABC में,
AD || BC और AC एक तिर्यक रेखा है जो इन दोनों समांतर रेखाओं को क्रमश: बिंदु A और बिंदु C पर काटती है।
हम जानते हैं कि यदि एक तिर्यक रेखा दो समांतर रेखाओं को काटती है तो एकांतर अंत: कोणों का प्रत्येक युग्म बराबर होता है।
यहाँ ∠DAC और ∠BCA एकांतर अंत: कोणों का युग्म है, अत: आपस में बराबर हैं।
अर्थात ∠DAC=∠BCA
उसी प्रकार ∠CAB और ∠ACD एकांतर अंत: कोणों का युग्म है, अत: आपस में बराबर हैं।
अत: ∠CAB=∠ACD
और भुजा AC दोनों त्रिभुजों में उभयनिष्ठ (common) है।
यहाँ दो कोण और उन दोनों कोणों के बीच की भुजा आपस में बराबर है।
अत: ASA (कोण भुजा कोण) सर्वांगसमता नियम से
ΔACD≅ΔABC
अत: CPCT के अनुसार हम जानते हैं कि सर्वांगसम त्रिभुजों मे संगत भाग बराबर होते हैं
∠ABC=∠CDA - - - - - (i)
उसी प्रकार △ABD और △BCD में,
DC||AB
और एक तिर्यक रेखा DB दोनों समांतर रेखाओं DC और AB काटती है अत: इस प्रकार बने हुए एकांतर अंत: कोणों के युग्म बराबर होंगे।
अत: ∠ABD=∠BDC
और, ∠CDA=△DBC
और भुजा DB दोनों त्रिभुजों ABD और BCD में उभयनिष्ठ (common) है।
अत: ASA (कोण भुजा कोण) सर्वांगसमता नियम से,
△ABD≅△BCD
अब CPCT के अनुसार हम जानते हैं कि सर्वांगसम त्रिभुजों मे संगत भाग बराबर होते हैं
∠DAB=∠BCD - - - - - (ii)
अब समीकरण (i) और समीकरण (ii) से
∠ABC=∠CDA और ∠DAB=∠BCD प्रमाणित
अत: एक समांतर चतुर्भुज में सम्मुख कोण बराबर होते हैं।
प्रमेय 5
यदि एक चतुर्भुज में सम्मुख कोणों का प्रत्येक युग्म बराबर हो तो वह चतुर्भुज समान्तर चतुर्भुज होता है।
माना कि ABCD एक चतुर्भुज है। और इसकी सम्मुख कोण ∠A=∠C और ∠B=∠D
सिद्ध करना है कि ABCD एक समांतर चतुर्भुज है ।

चूंकि चतुर्भुज के चारों कोणों का योग 360∘ होता है
∠A+∠B+∠C+∠D=360∘
∠A+∠B+∠A+∠B=360∘
2(∠A+∠B)=360∘
∠A+∠B=180∘
हम देख सकते हैं दो क्रमागत कोणों का योग 180∘ है।
चूंकि हम जानते हैं, दो समांतर रेखाओं को काटने वाली तिर्यक रेखा से बनने वाले क्रमागत अन्तः कोणों का युग्म संपूरक होता है
इसलिए AD||BC
इसीप्रकार AB||CD
अतः ABCD एक समांतर चतुर्भुज है।
प्रमेय 6
समांतर चतुर्भुज के विकर्ण एक दूसरे को परस्पर समद्विभाजित करते है।
जैसा कि दिया गया है,
माना कि ABCD एक समांतर चतुर्भुज हैं और, AC और DB इस चतुर्भुज के दो विकर्ण हैं।
अत: सिद्ध करना है कि AC और DB एक दूसरे को समद्विभाजित करते हैं।
अर्थात OA = OC और OB=OD
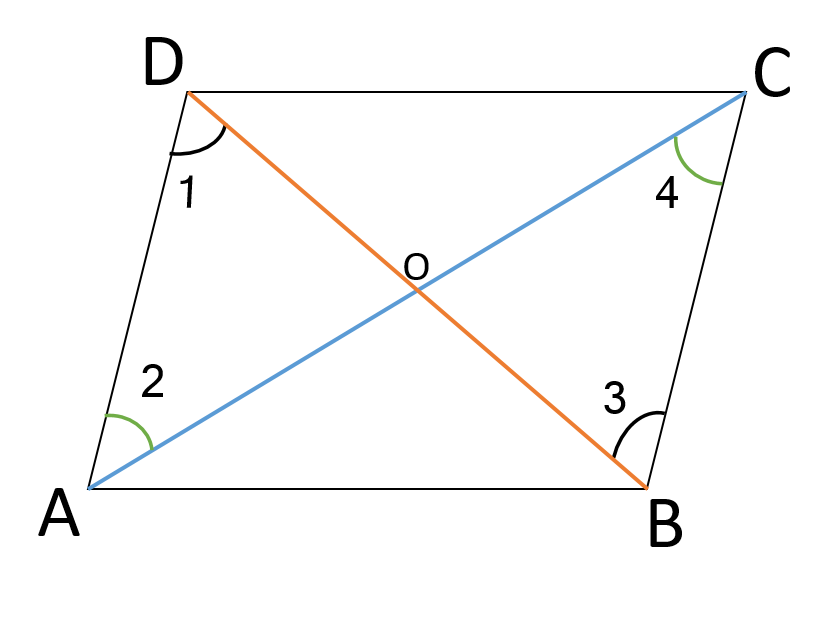
चूँकि ABCD एक समांतर चतुर्भुज है,
अत: AD =BC और AD||BC
अब △AOD और △BOC में,
AD||BC और एक तिर्यक रेखा AC इन्हें काटती है, अत: एकांतर अंत: कोणों का प्रत्येक युग्म आपस में बराबर होंगे।
अत: ∠2=∠4 - - - - - (i)
उसी प्रकार, AD||BC और एक तिर्यक रेखा BD इन्हें काटती हैं, अत: एकांतर अंत: कोणों का प्रत्येक युग्म बराबर होंगे।
अत: ∠1=∠3 - - - - (ii)
और, AD = BC [चूँकि समांतर चतुर्भुज की सम्मुख भुजाएँ हैं।]
अत: ASA (कोण भुजा कोण) सर्वांगसमता नियम से,
△AOD≅△BOC
अब CPCT नियम से हम जानते हैं कि सर्वांगसम त्रिभुजों मे संगत भाग बराबर होते हैं,
अत: OA=OC और OD = OB
अत: समांतर चतुर्भुज के विकर्ण एक दूसरे को परस्पर समद्विभाजित करते हैं। प्रमाणित
प्रमेय 7
यदि एक चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करे तो वह एक समांतर चतुर्भुज होगा।
जैसा कि दिया गया है
माना कि ABCD चतुर्भुज है और AC और DB इसके विकर्ण हैं, जो एक दूसरे को समद्विभाजित करते हैं।
अर्थात, OA = OC और OD= OB
अत: सिद्ध करना है कि ABCD एक समांतर चतुर्भुज है।
अर्थात सिद्ध करना है कि AB||DC और AD||BC
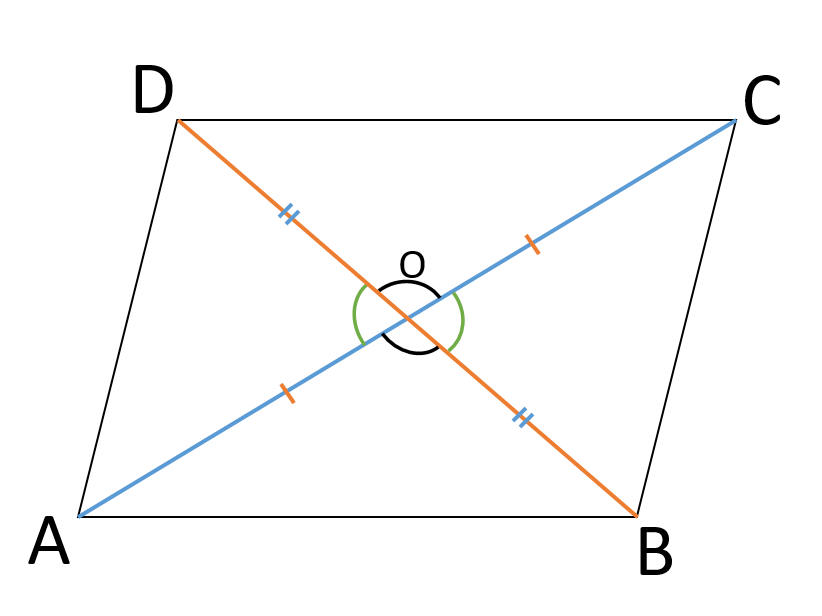
△AOB और △DOC में,
OD= OB और OA = OC
[चूँकि विकर्ण एक दूसरे को समद्विभाजित करते हैं।]
और ∠AOB=∠DOC
[चूँकि ∠AOB और ∠DOC शीर्षाभिमुख कोण हैं, तदानुसार बराबर हैं।]
अत: SAS (भुजा कोण भुजा) सर्वांगसमता नियम से,
△AOB≅△DOC
अब CPCT के अनुसार हम जानते हैं कि सर्वांगसम त्रिभुजों मे संगत भाग बराबर होते हैं
अत: ∠ODC=∠OBA - - - - - (i)
यहाँ तिर्यक रेखा DB दो रेखाओं AB और DC को इस प्रकार काटती है कि एकांतर अंत: कोणों का प्रत्येक युग्म आपस में बराबर हैं।
अत: हम जानते हैं कि समांतर रेखाओं की एक प्रमेय के अनुसार यदि कोई तिर्यक रेखा दो रेखाओं को इस प्रकार काटती है कि उनसे बने एकांतर अंत: कोणों का प्रत्येक युग्म आपस में बराबर हों, तो रेखाएँ समांतर होती हैं।
अत: AB||DC
उसी प्रकार △AOD और △COB में,
OA = OC और OB =OD
[चूँकि दिया गया है कि विकर्ण एक दूसरे को समद्विभाजित करते हैं।]
और ∠AOD और ∠COB उर्ध्वाधर सम्मुख कोण हैं तदनुसार बराबर हैं।
अर्थात ∠AOD=∠COB
अत: SAS (भुजा कोण भुजा) सर्वांगसमता नियम से,
△AOD≅△COB
अब CPCT के अनुसार हम जानते हैं कि सर्वांगसम त्रिभुजों मे संगत भाग बराबर होते हैं |
अत: ∠ODA=∠OBC - - - - (ii)
यहाँ एक तिर्यक रेखा DB दो रेखाओं AD और BC को इस प्रकार काटती हैं कि बने हुए एकांतर अंत: कोण बराबर हैं।
अत: AD||BC
अब चूँकि AB||DC और AD||BC
अत: ABCD एक समांतर चतुर्भुज हैं |
अत: यदि एक चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करें, तो वह एक समांतर चतुर्भुज होता है।प्रमाणित
उदाहरण 6
दर्शाइए कि एक समांतर चतुर्भुज के कोणों के समद्विभाजक एक आयत बनाते हैं।
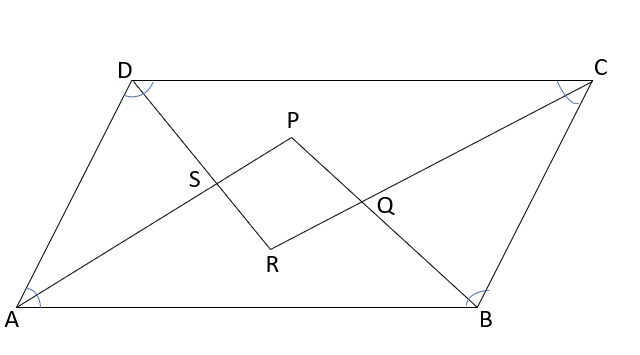
मान लीजिए P,Q,R और S क्रमशः समांतर चतुर्भुज ABCD के ∠A और ∠B,∠C और ∠D के समद्विभाजकों के प्रतिच्छेद बिंदु हैं
:DS कोण D को और AS कोण A को समद्विभाजित करते हैं इसलिए
ΔASD में
∠DAS+∠ADS
=12∠A+12∠D
=12(∠A+∠D)
=12×180∘
(∠A और ∠D तिर्यक रेखा के एक ही ओर अंतः कोण है।)
=90∘
साथ ही
∠DAS+∠ADS+∠DSA=180∘
(त्रिभुज के अंतः कोणों का योग 180∘होता है । )
या
90∘+∠DSA=180∘
या
∠DSA=90∘
अतः ∠PSR=90∘
(शीर्षाभिमुख कोण)
इसी प्रकार
∠APB=90∘
या ∠SPQ=90∘
∠PQR=90∘ और
∠SRQ=90∘ है।
इसलिए PQRS एक ऐसा चतुर्भुज है जिसके सभी कोण समकोण हैं।
स्पष्टतः यह एक आयत है क्योंकि इसके सम्मुख कोणों के दोनों युग्म बराबर है।
उदाहरण 7
माना ABCD एक समान्तर चतुर्भुज है तथा AP व CQ क्रमशः बिन्दु A व C से विकर्ण पर डाले गए लम्ब है। सिद्ध कीजिए की AP=CQ
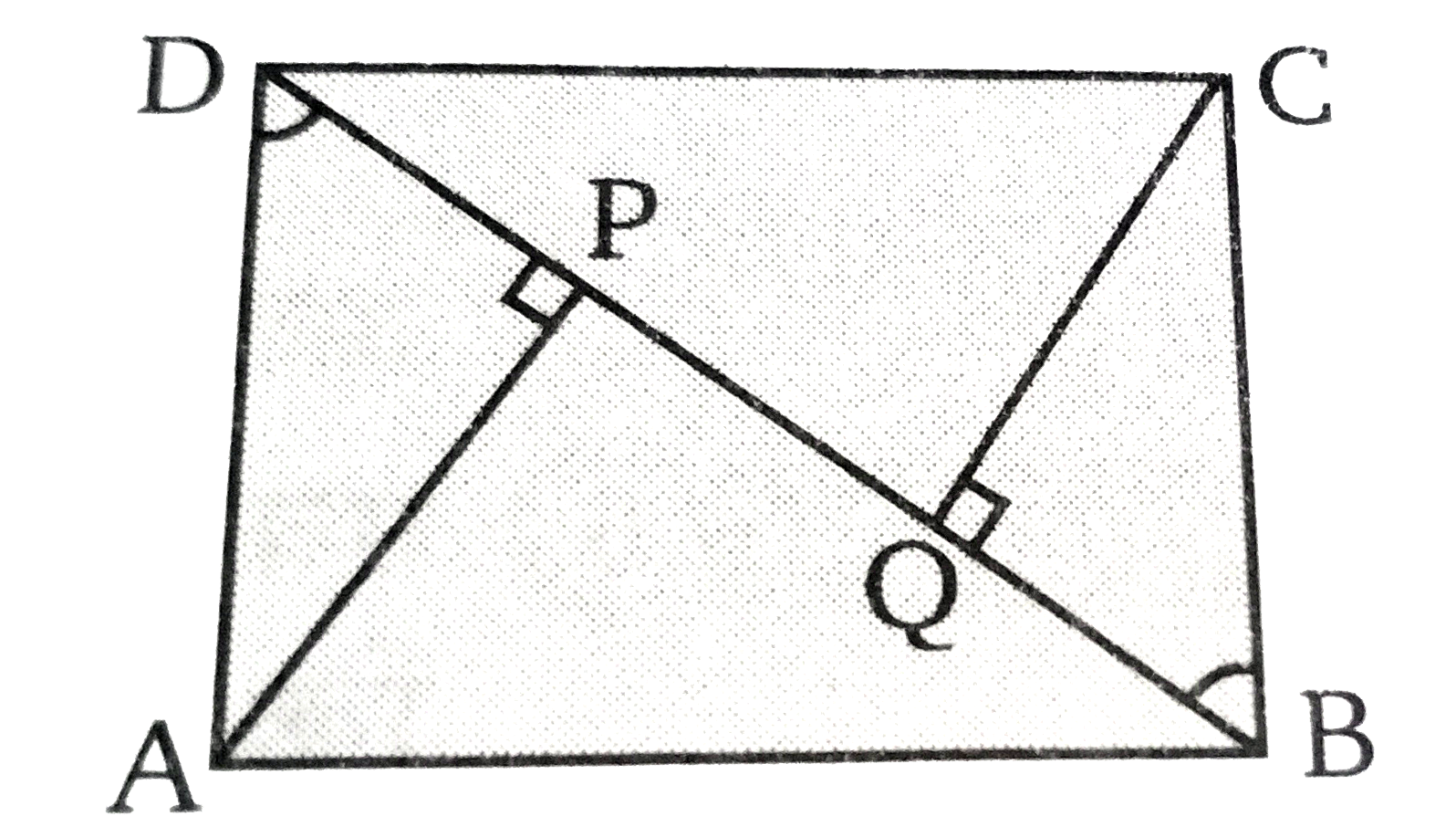
ΔAPD व ΔBQC में
[ चूंकि ABCD एक समान्तर चतुर्भुज है ]
इसलिए AD=BC
[ चूंकि AD||BC व BD तिर्यक रेखा है। ]
अतः
∠ADP=∠CBQ
( एकान्तर कोण )
∠APD=∠CQB [ प्रत्येक 90∘]
∴ΔAPD≅BQC [ AAS सर्वांगसम ]
अतः AP=CQ
[CPCT]
मध्य बिंदु प्रमेय
बच्चों आप एक त्रिभुज और एक चतुर्भुज के अनेक गुणों का अध्ययन कर चुके हैं। आइए अब इसके एक अन्य गुण का अध्ययन करे जो कि एक त्रिभुज की भुजाओं के मध्य बिंदुओं से जुड़ी है।
इससे सम्बन्धित दो प्रमेय है :
प्रमेय I
किसी त्रिभुज में किन्ही दो भुजाओ के मध्य बिंदुओ से होकर जाने वाली रेखाखण्ड तीसरी भुजा के समांतर होती है।
माना कि,
ABC एक त्रिभुज है तथा D और E क्रमश: भुजाओं AB और AC के मध्य बिंदु हैं।
अत: सिद्ध करना है कि DE∣∣BC
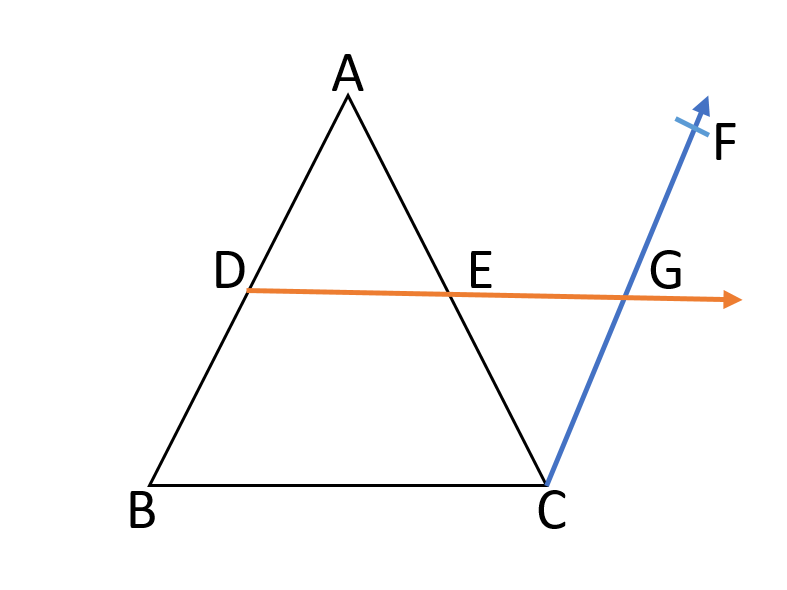
एक रेखा CF भुजा AB के समांतर खींची गयी और, रेखा DE को बढ़ाया गया जो रेखा CF को बिंदु G पर काटती है।
त्रिभुज ADE और त्रिभुज ECG में,
बिंदु E भुजा AC का मध्य बिंदु है। [ दिया गया है]
अत: AE=EC
AB∣∣CF [चित्रानुसार]
AC एक तिर्यक रेखा है जो दो समांतर रेखाओं AB और CF को काटती है। अत: एकांतर अंत: कोण बराबर होंगे।
अर्थात ∠DAE=∠ECG
अर्थात ∠DEA=∠GEC [शीर्षाभिमुख कोण से]
अत: ASA (कोण भुजा कोण) सर्वांगसमता नियम से
△ADE≅△ECG
अब CPCT नियम से हम जानते हैं कि सर्वांगसम त्रिभुजों मे संगत भाग बराबर होते हैं।
अत: DE=EG - - - - (i)
और AD=CG
⇒ AD = CG = DB
[चूँकि बिंदु D भुजा AB का मध्य बिंदु है अत: AD=DB]
अब चूँकि DB=CG और DB∣∣CG
चूँकि एक चतुर्भुज में यदि सम्मुख भुजाएँ बराबर और समांतर हों, तो वह चतुर्भुज एक समांतर चतुर्भुज होता है।
अत: DBCG एक समांतर चतुर्भुज है।
अत: DG∣∣BC
इस प्रकार DE∣∣BC - - - - (ii)
अब चूँकि DBCG एक समांतर चतुर्भुज है तथा एक समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं।
अत: DG=BC
⇒ DE+EG =BC
⇒DE+DE=BC (चूंकि DE=EG)
[ समीकरण (i) से]
⇒2DE =BC
⇒DE=12BC - - - - (iii)
समीकरण (ii) और समीकरण (iii) से
DE∣∣BC और DE=12BC
अत: किसी त्रिभुज की किन्हीं दो भुजाओं के मध्य बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के समांतर और आधा होता है। [प्रमाणित]
प्रमेय II
किसी त्रिभुज की एक भुजा के मध्य बिंदु से दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।
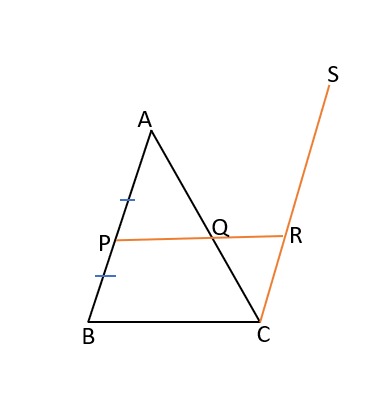
माना कि ABC एक त्रिभुज है,
जहाँ बिंदु P भुजा AB का मध्य-बिंदु है।
सिद्ध करना है
AQ=QC
यहाँ एक रचना करते है जहाँ भुजा AB के समांतर रेखा CS खींचते है, अब बिन्दु P से BC के समांतर एक रेखा PQ खींचते है अर्थात BC∣∣PQ, साथ ही PQ को आगे बढ़ाते है जो की CS को R मे प्रतिच्छेद करती है।
समांतर चतुर्भुज PRCB में,
PB∣∣CR [रचना से]
PR∣∣BC [दिया है]
चूंकि PRBC एक समांतर चतुर्भुज है ।
अतः PR=BC तथा
PB=RC
[चूंकि P, भुजा AB का मध्य बिन्दु है।]
AP=PB
अतः AP=RC - - - - (i)
△APQ व △QRC में
∠AQP=∠RQC [ शीर्षाभिमुख कोण युग्म ]
AP=RC [समीकरण 1 से ]
∠QRC=∠QPA [चूंकि AB∣∣CS अतः एकांतर कोण से]
AAS सर्वांगसमता के नियम से
△APQ≅△QRC
अतः AQ=QC
उदाहरण 8
E व F क्रमशः समतल चतुर्भुज ABCD की असमान्तर भुजाओं के मध्य बिन्दु है। सिद्ध कीजिए की
(i) EF∣∣AB
(ii)EF=12(AB+CD)
B व E को मिलाये तथा इसे इतना बढ़ाये की यह बिन्दु P पर CD से मिले
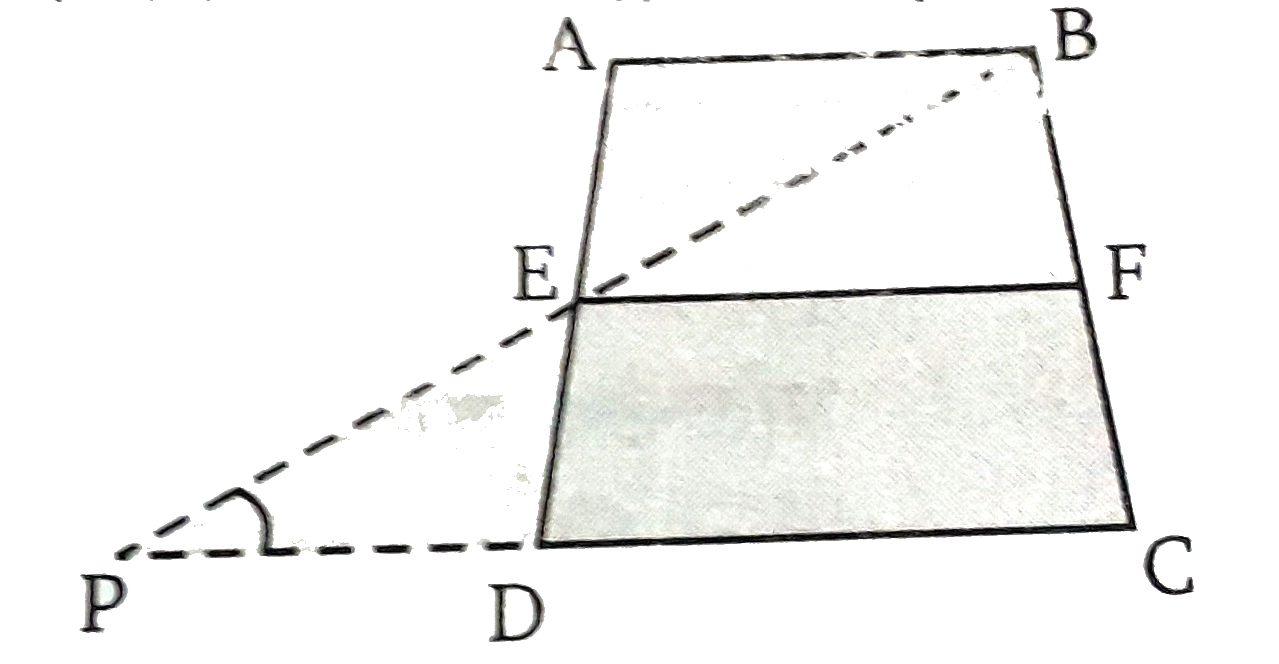
त्रिभुज AEB व त्रिभुज DEP में,
AE=ED
[ ∴E,AD का मध्य बिन्दु है ]
∠ABE=∠EPD (एकान्तर कोण)
[ ∴AB||PC व तिर्यक रेखा BP,B व P पर इनसे मिलती है।]
∠AEB=∠PED
[शीर्षाभिमुख कोण]
∴ΔAEB≅ΔDEP
⇒BE=PE
[CPCT] ....(1)
व AB=DP
[CPCT ] ....(2)
अब ΔBPC में E व F क्रमशःBP वBC के मध्य बिन्दु है।
∴EF||PC व EF=12PC
अथार्त EF||AB व EF=12(PD+DC)
=12(AB+DC)
[ समीकरण (2) से]
अतः EF||AB व EF=12(AB+DC)
उदाहरण 9
त्रिभुज ABC में बिन्दु M व N क्रमशः AB व AC पर बिन्दु है तथा AM=14AB व AN=14AC
सिद्ध कीजिए की MN=14BC
मानाM' व N' क्रमशः भुजा AB व AC के मध्य बिन्दु है तथा M व N क्रमशः AM' वAN' के मध्य बिन्दु है।
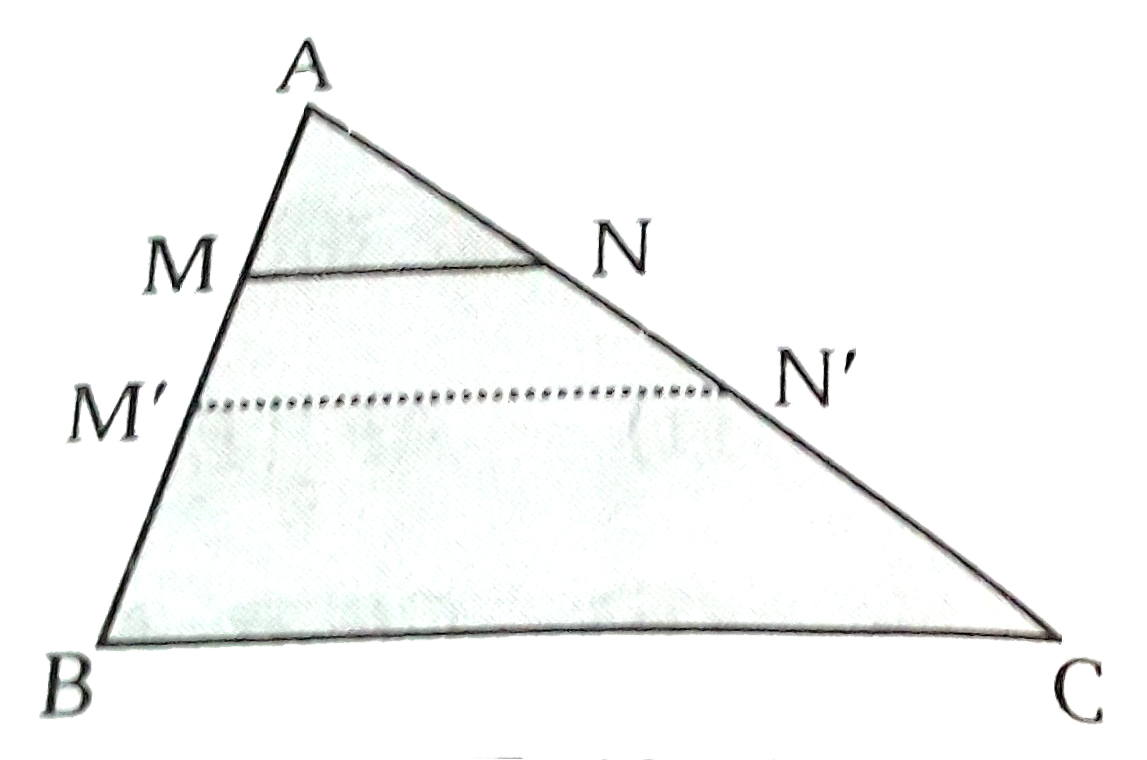
ΔAM'N' में M और N क्रमशः AM' व AN' के मध्य बिन्दु है।
∴MN=12M'N' ...(1)
इसी प्रकार ΔABC में M' व N' क्रमशः AB व AC के मध्य बिन्दु है ।
∴M'N'=12BC ...(2)
समीकरण (1) व (2) से
MN=12M'N'
=12(12BC)
=14BC
उदाहरण 10
ABC एक त्रिभुज है जिसका कोण C समकोण है। कर्ण AB के मध्य बिंदु M से होकर BC के समांतर खींची गई रेखा AC को D पर प्रतिच्छेद करती है। दर्शाइए कि:
(i) D भुजा AC का मध्य-बिंदु है।
(ii) MD⊥AC है।
(iii) CM=MA=12AB है।

(i) ΔABC में भुजा AB का मध्य बिंदु M है, [ प्रश्नानुसार दिया है । ]
मध्य बिंदु प्रमेय के विलोम के अनुसार-
∴AD=DC
अतः AC का मध्य बिंदु D है।
(ii) माना कि भुजा BC के समांतर खींची गई रेखा m है। ( दिया है )
तथा तिर्यक रेखा AC है।
∴∠1=∠C ( संगत कोण )
या ∠1=90∘ [ ∠C=90∘] (दिया है।)
अतः MD⊥AC
(iii) आकृति में बने ΔAMD तथा ΔCMD में
∠1=∠2=90∘ ( सिद्ध कर चुके है। )
AD=DC ( सिद्ध कर चुके हैं। )
तथा MD=MD ( उभयनिष्ठ भुजाएं )
अतः ΔAMD≅ΔCMD (S.A.S. से)
∴AM=CM (c.p.c.t)
दिया है कि AB भुजा का मध्य बिंदु M है।
∴AM=12AB……(2)
समीकरण 1 व 2 से
CM=AM=12AB
सारांश
इस अध्याय में, आपने निम्नलिखित बिंदुओं का अध्ययन किया है :
1. किसी चतुर्भुज के कोणों का योग 360∘ होता है।
2. समांतर चतुर्भुज का एक विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभाजित करता है।
3. एक समांतर चतुर्भुज में,
(i) सम्मुख भुजाएँ बराबर होती हैं।
(ii) सम्मुख कोण बराबर होते हैं।
(iii) विकर्ण परस्पर समद्विभाजित करते हैं।
4. एक चतुर्भुज, समांतर चतुर्भुज होता है, यदि
(i) सम्मुख भुजाएँ बराबर हों या
(ii) सम्मुख कोण बराबर हों या
(iii) विकर्ण परस्पर समद्विभाजित करते हों या
(iv) सम्मुख भुजाओं का एक युग्म बराबर हो और समांतर हो।
5. आयत के विकर्ण परस्पर समद्विभाजित करते हैं और बराबर होते हैं। इसका विलोम भी सत्य है।
6. समचतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं। इसका विलोम भी सत्य है।
7. वर्ग के विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं और बराबर होते हैं। इसका विलोम भी सत्य है।
8. किसी त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के समांतर होता है और उसका आधा होता है।
9. किसी त्रिभुज की एक भुजा के मध्य-बिंदु से दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।
10. किसी चतुर्भुज की भुजाओं के मध्य-बिंदुओं को एक क्रम से मिलाने वाले रेखाखंडों द्वारा बना चतुर्भुज एक समांतर चतुर्भुज होता है।