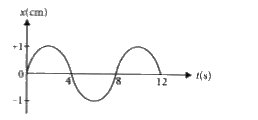
The (x - t) graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at t=4/3s is
 .
.
A
√332π2cm/s2
B
−π232cm/s2
C
π232cm/s2
D
−√332π2cm/s2
Video Solution
Text Solution
The correct Answer is:D
From the graph it is clear that the amplitude is 1cm and the period is 8second. Therefore the equation for the (S.H.M.) is
x=asin(2πT×t=1sin(2π8)t=sin(π4)t
The velocity (v) of the particle at any instant of time 't' is
v=dxdt=ddt[sin(π4)t]=π4cos(π4)t
The acceleration of the particle is
d2xdt2=−(π4)2sin(π4)t
At t=43s we get
d2xdt2=−(π4)2sinπ4×43=−π216sinπ3
= −√(3π2)32cm/s2.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
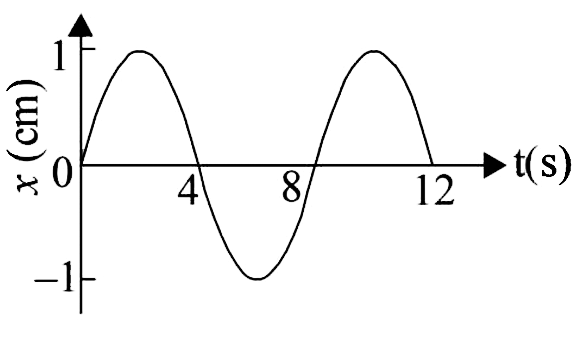
The x−t graph of a particle undergoing simple harmonic motion is shown below. The accelertion of the particle at t=4/3s is
 A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2
A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2The x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle of t=4/3s is
 A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2
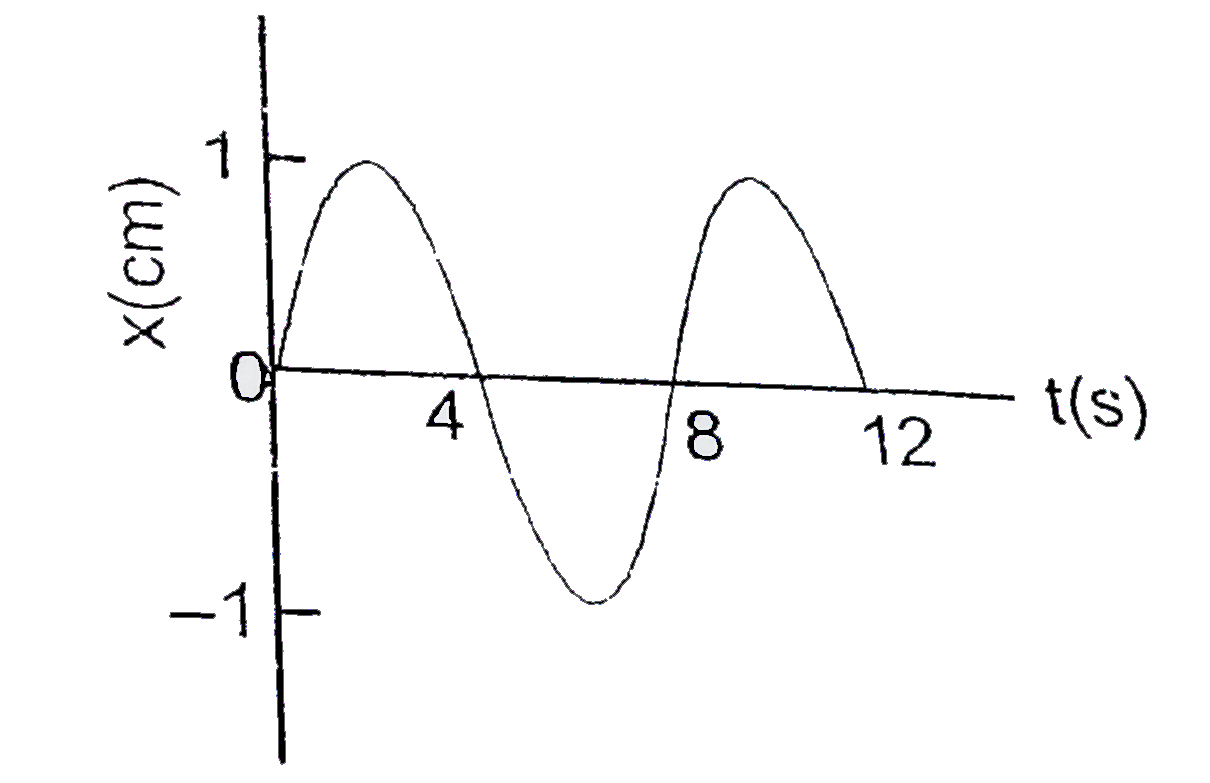
A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2The x−t graph of a particle undergoing simple harmonic motion is shown in figure. Acceleration of particle at t=4/3s is
 A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2
A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2
The displacement vs time graph of a particle undergoing S.H>M. Is shown below . The acceleration of the particle at t=2/3s is

View SolutionThe velocity -time (v−t) graph of a particle moving in a straight line is shown in figure. The acceleration of the particle at t=9 is:
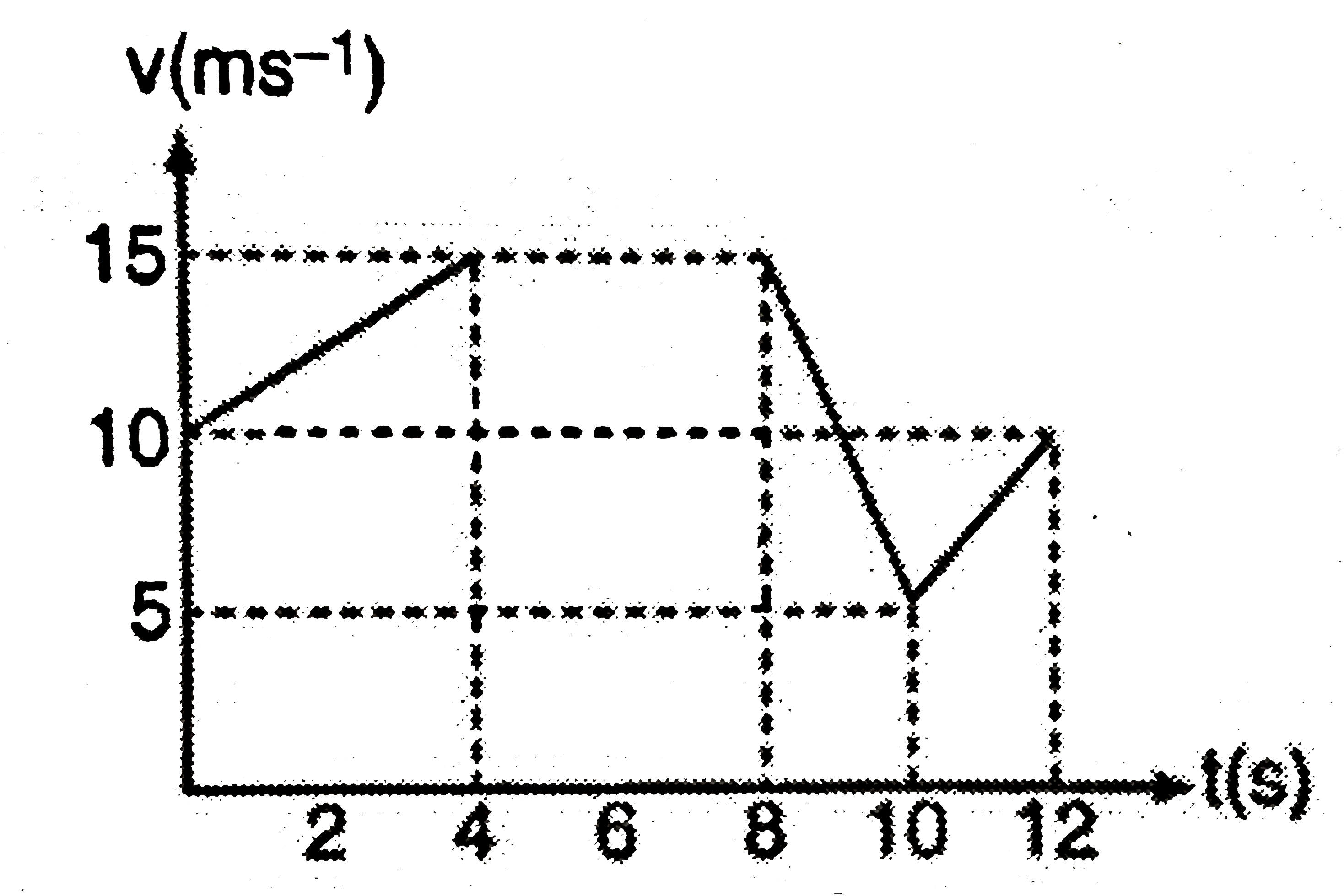
View SolutionThe phase (at a time t) of a particle in simple harmonic motion tells
View SolutionThe velovity-time graph of a particle moving in a straitht line is shown in . The acceleration of the particle at t=9s is.
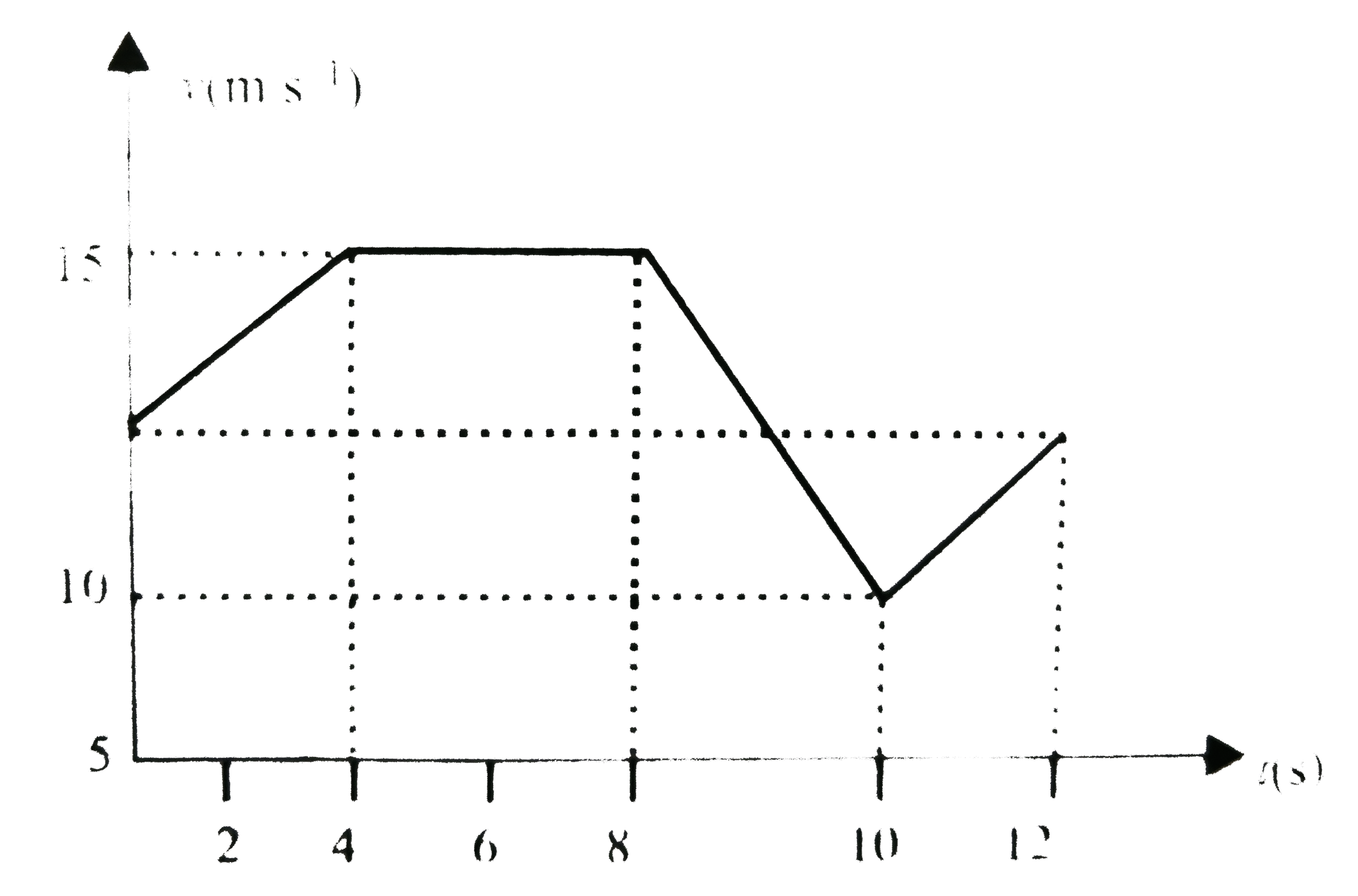 .
.
View SolutionIf a particle is executing simple harmonic motion, then acceleration of particle
View Solution