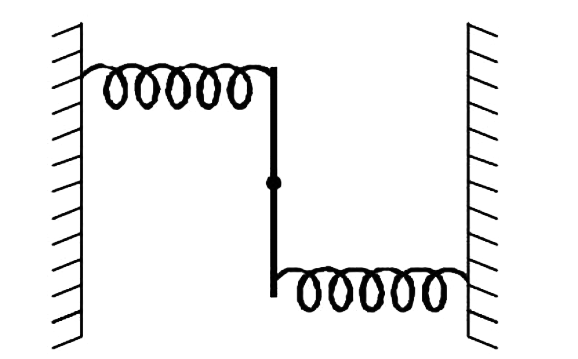
A uniform rod of length L and mass M is pivoted at the centre. Its two ends are attached to two springs of equal spring constants k. The springs are fixed to rigid supports as shown in the figure, and the rod is free to oscillate in the horizontal plane. The rod is free to oscillate in the horizontal plane. The rod is gently pushed through a small angle (θ) in one direction and released. The frequency of oscillation is. ?
 .
.
12π√2kM
12π√kM
12π√6kM
12π√24kM
The correct Answer is:C
Figure shows that rod at an angle (theta) with respect to its equilibrium position. Both the springs are streched by length lθ2
(##JMA_CHMO_C10_009_S01##).
The restoring torque due to the springs.
τ=−2 (Restoring force) xx perpendicular distance
τ=−2k(lθ2)×l2=−kl22θ....(i) ltbRgt If (I) is the moment of interia of the rod about (M) then
τ=I∝=Id2θdt2 ....(ii)
From (i) & (ii) we get
Id2θdt2=−l2θ2⇒d2θdt2=−kIl22θ=−kMl2/12l22θ
Comparing it with the standard equation of rotational (SHM) we get
d2θdt2=−ω2θ⇒ω2=6kM⇒ω=√6kM
⇒2πv=√6kM⇒v=12π√6kM.
Topper's Solved these Questions
Similar Questions
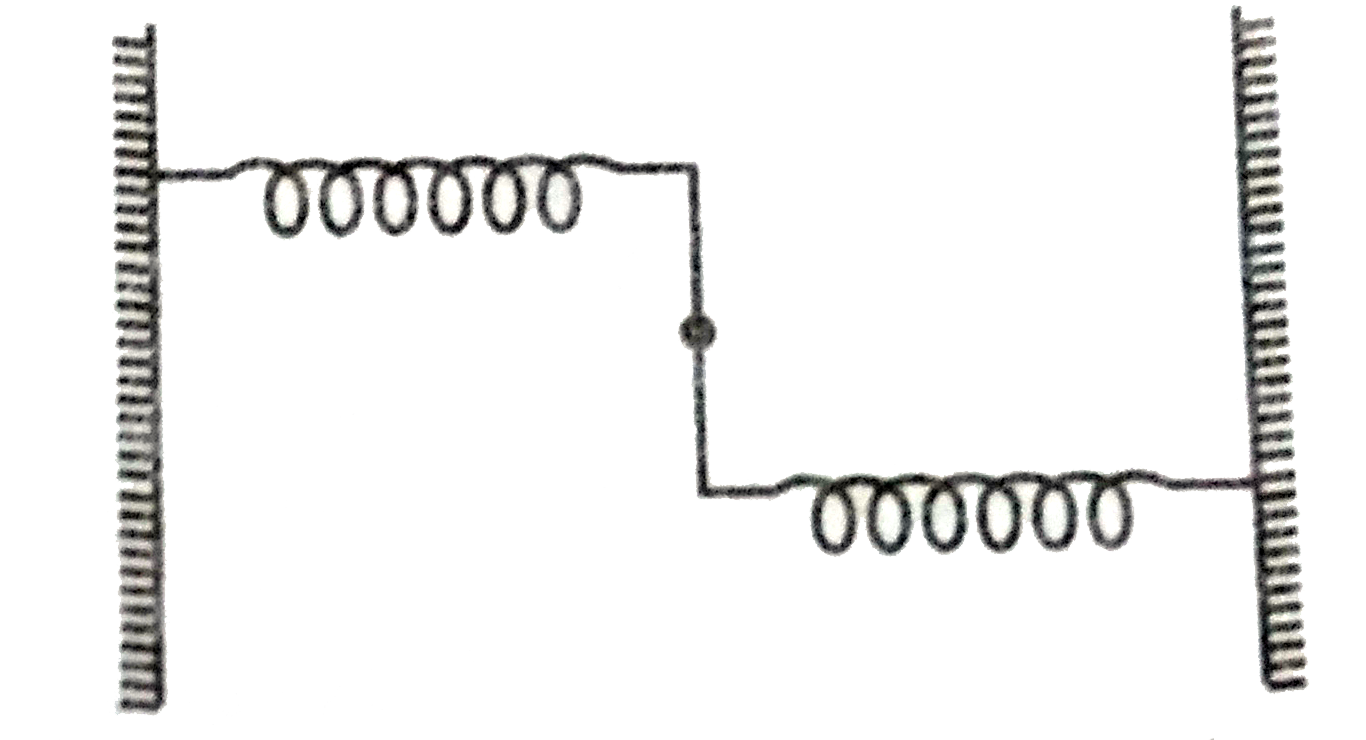
A uniform rod of length l and mass M is pivoted at the centre. Its two ends are attached to two ends are attached to two springs of equal spring constant k. the springs are fixed to rigid support as shown in figure and the rod is free to oscillate in the horizontal plane. the rod is gently pushed through a small angle θ in one direction and released. the frequency of oscillation is
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View Solution
Knowledge Check
A uniform rod of length L and mass M is pivotedat the centre. Its two ends are attached to two springs of equal spring constants. k. The springs as shown in the figure, and the rod is free to oscillate in hte horizontal plane. the rod is gently pushed through a small angle θ in one direction and released. the frequency of oscilllation is-
 A12π√2kMB12π√kMC12π√6kMD12π√24kM
A12π√2kMB12π√kMC12π√6kMD12π√24kMThe arrangement shown of a uniform rod of length l and mass m, pivoted at the centre and its two ends attached to two springs of spring constant K1 and K2 . The other end of springs are fixed to two rigid supports the rod which is free to rotate in the horizontal plane , is pushed by a small angle in one direction and released . Teh frequency of oscillation of the rod is
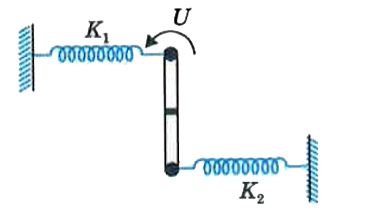 A12π√K1+K2mB12π√K1+K23mC12√3π√K1+K2mD√32π√K1+K2m
A12π√K1+K2mB12π√K1+K23mC12√3π√K1+K2mD√32π√K1+K2mA bob of mass m is connected to a spring of spring constant k and a string which is fixed to the ceiling as shown in figure. Original length of the spring is L and the bob rotates in a horizontal circle centred at the fixed rod. Assuming the spring remains horizontal, then elongation in the spring is :
 A(mg−mω2L)tanθmω2+kBmgtanθ+mω2Lmω2−kCmgtanθ+mω2LkDgtanθ−ω2Lω2−k/m
A(mg−mω2L)tanθmω2+kBmgtanθ+mω2Lmω2−kCmgtanθ+mω2LkDgtanθ−ω2Lω2−k/m
A straight rod of light L and mass m is pivoted freely from a point of the roof. Its lower end is connected to an ideal spring of spring constant K. The other end of the spring is connected to the wall as shown in the figure. Find the frequency of small oscillation of the system.
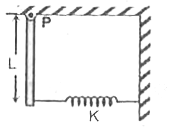
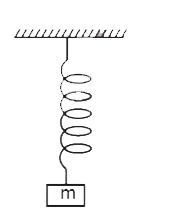
View SolutionA mass m is attached to the free end of a massless spring of spring constant k with its other end fixed to a rigid support as shown in figure. Find out the time period of the mass, if it is displaced slightly by an amount x downward.
View Solutiontwo light identical springs of spring constant K are attached horizontally at the two ends of a uniform horizontal rod AB of length l and mass m. the rod is pivoted at its centre 'o' and can rotate freely in horizontal plane . The other ends of the two springs are fixed to rigid supportss as shown in figure . the rod is gently pushed through a small angle and released , the frequency of resulting oscillation is :
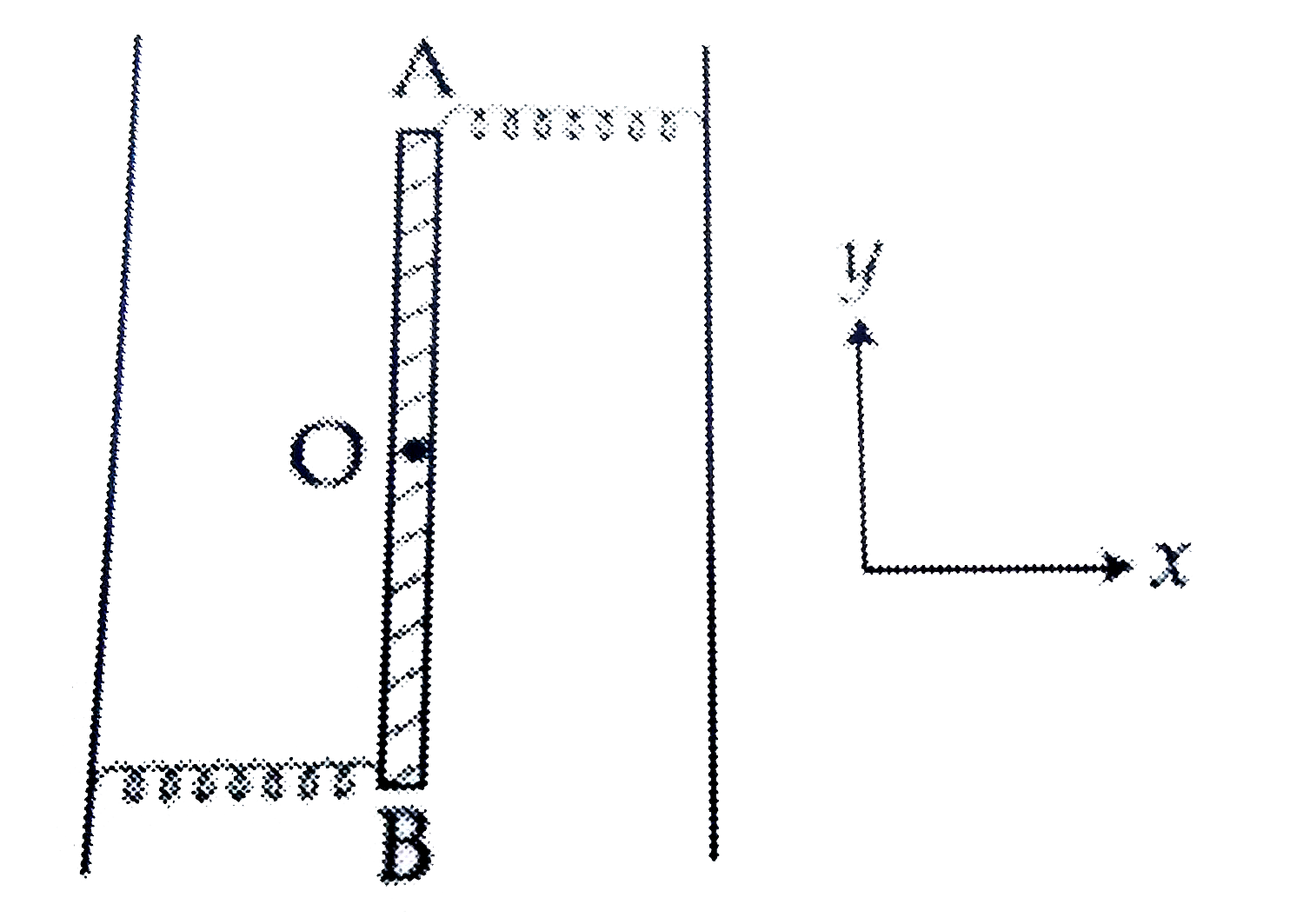
View SolutionA uniform rod of mass 2m and length L is hinged at one end and carries a particle of mass m at the other end.Two springs each of force constant k are installed at distances as shown.The whole arrangement rests on a smooth horizontal surface.The frequency of small oscillations will be?
View SolutionA rod of length l and mass m, pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant k. Find the frequency of small oscillations about the equilibrium position.
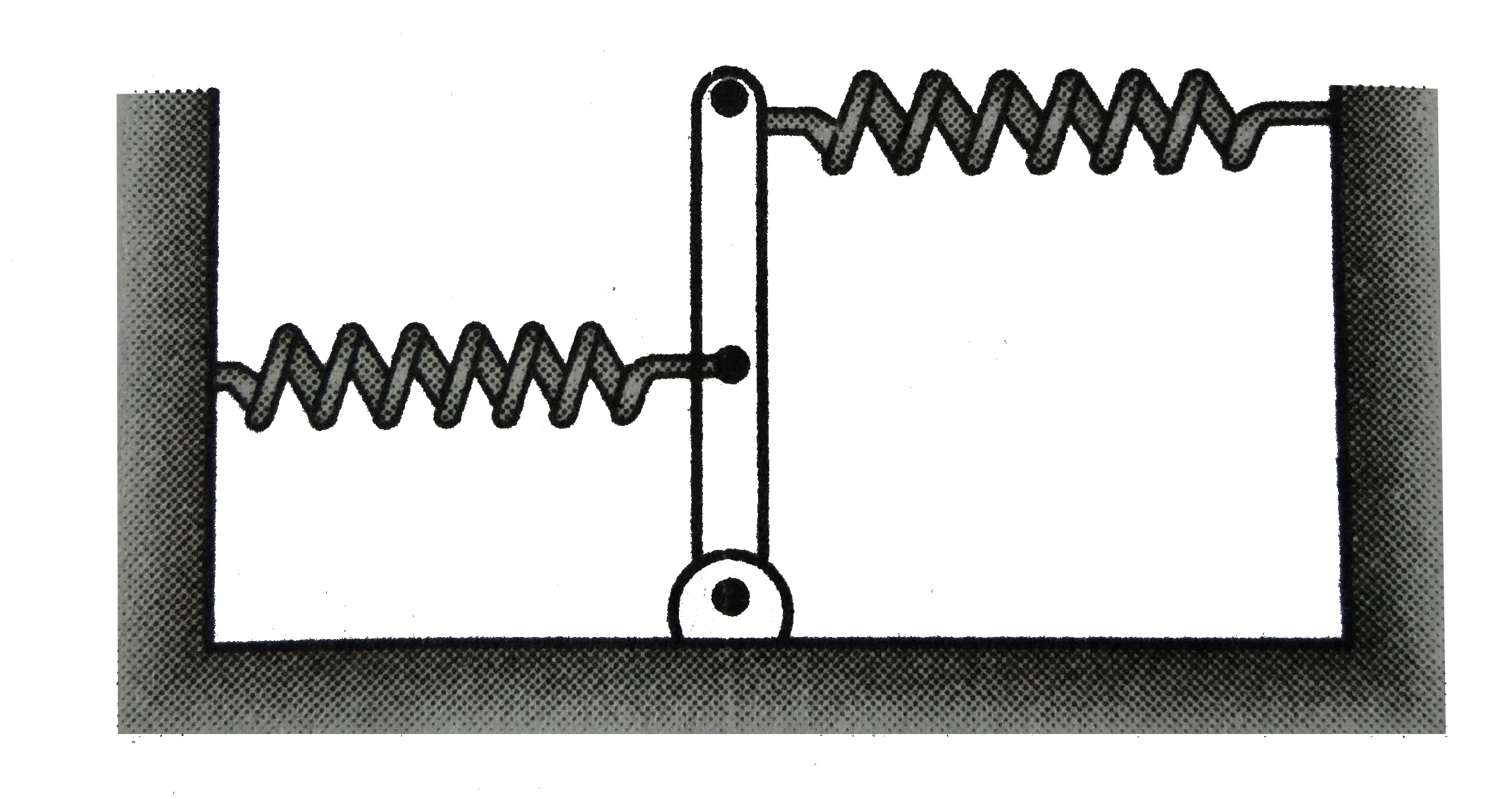
View Solution
