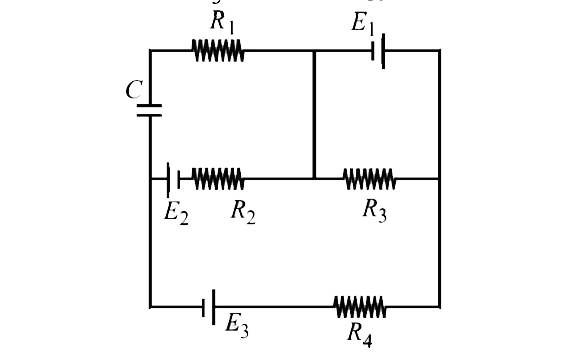
In the given circuit
E1=3E2=2E3=6vo<sR1=2R4=6ohms
R3=2R2=4ohmsC=5μf.
Find the current in R and the energy stored in the capacitor.
The correct Answer is:A, D
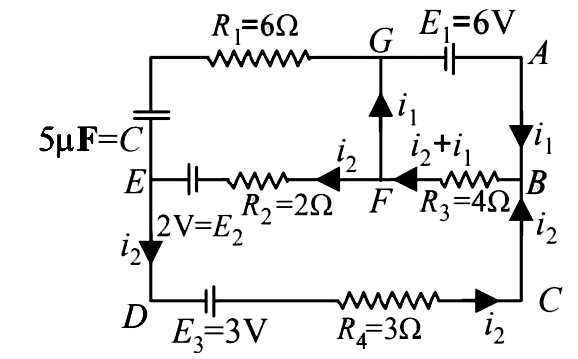
Applying Kirchoff's law in ABFGA
6−(i1+i2)4=0……….(i)
Applying Kirchoff's law in BCDEFB
i2×3−3−2+2i2+(i2+i1)4=0 ………………(ii)
Putting the value of 4(i1+i2)=6 in (ii) 3i2−5+2i2+6=0
∴i2=−15A
Substituting this value in (i) , we get
i1=1.5−(−15)=1.7A .
Thereforecurrent in R3
=i1+i2=1.7−0.2=1.5A
To find the p.d. across the capacitor
VE−2−0.2×2=VG
∴VE−VG=2.4V
or V=24V
∴E≠rgys→red∈∩aci→r=12CV2
=12×5×10−6×(2.4)2=1.44×10−5J .
Topper's Solved these Questions
Similar Questions
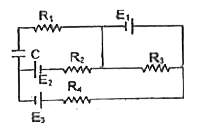
In the given circuit. E1=6vo<s,E2=2vo<s,E3=6vo<s
R1=6ΩR2=2ΩR3=4Oemga,R4=3Ω and C=5μF. Find the current in R3 and energy stored in the capacitor at steady state
View Solution
In the circuit shown in figure. ε1=3,ε2=2,ε3=6V,R1=2,R4=6Ω,R3=2,R2=4ΩandC=5μF. Find the current in the resistor R3 and the electrical energy stored in the capacitor C.
View Solution
Knowledge Check
In the circuit shown here, E1=E2=E3=2V and R1=R2=4ohms. The current flowing between point A and B through battery E2 is
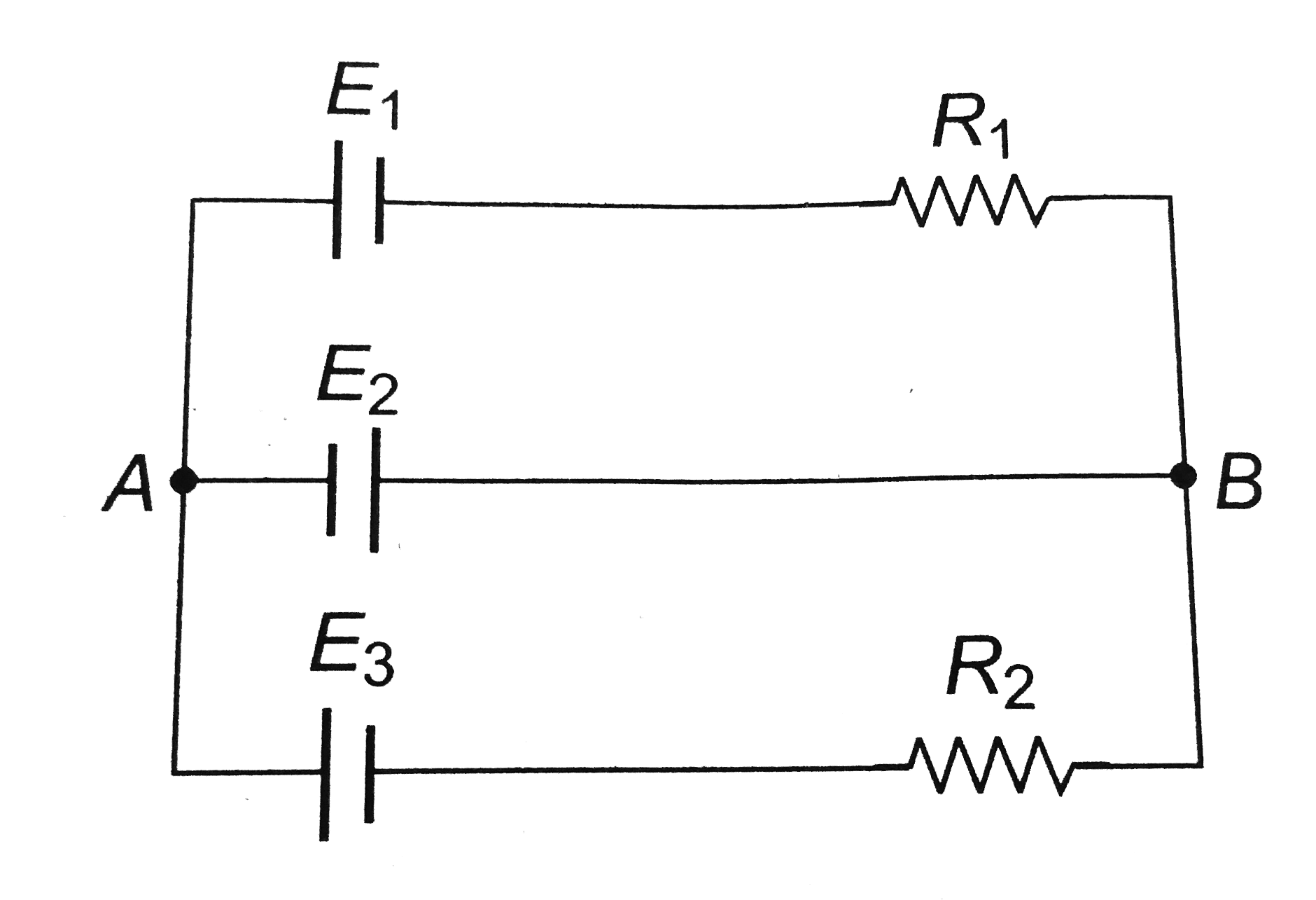 AZeroB2amp from A to BC2amp from B to ADNone of the above
AZeroB2amp from A to BC2amp from B to ADNone of the aboveIn the circuit given E=6.0V,R1=100ohms,R2=R3=50ohms,R4=75ohms. The equivalent resistance of the circuit, in ohms, is
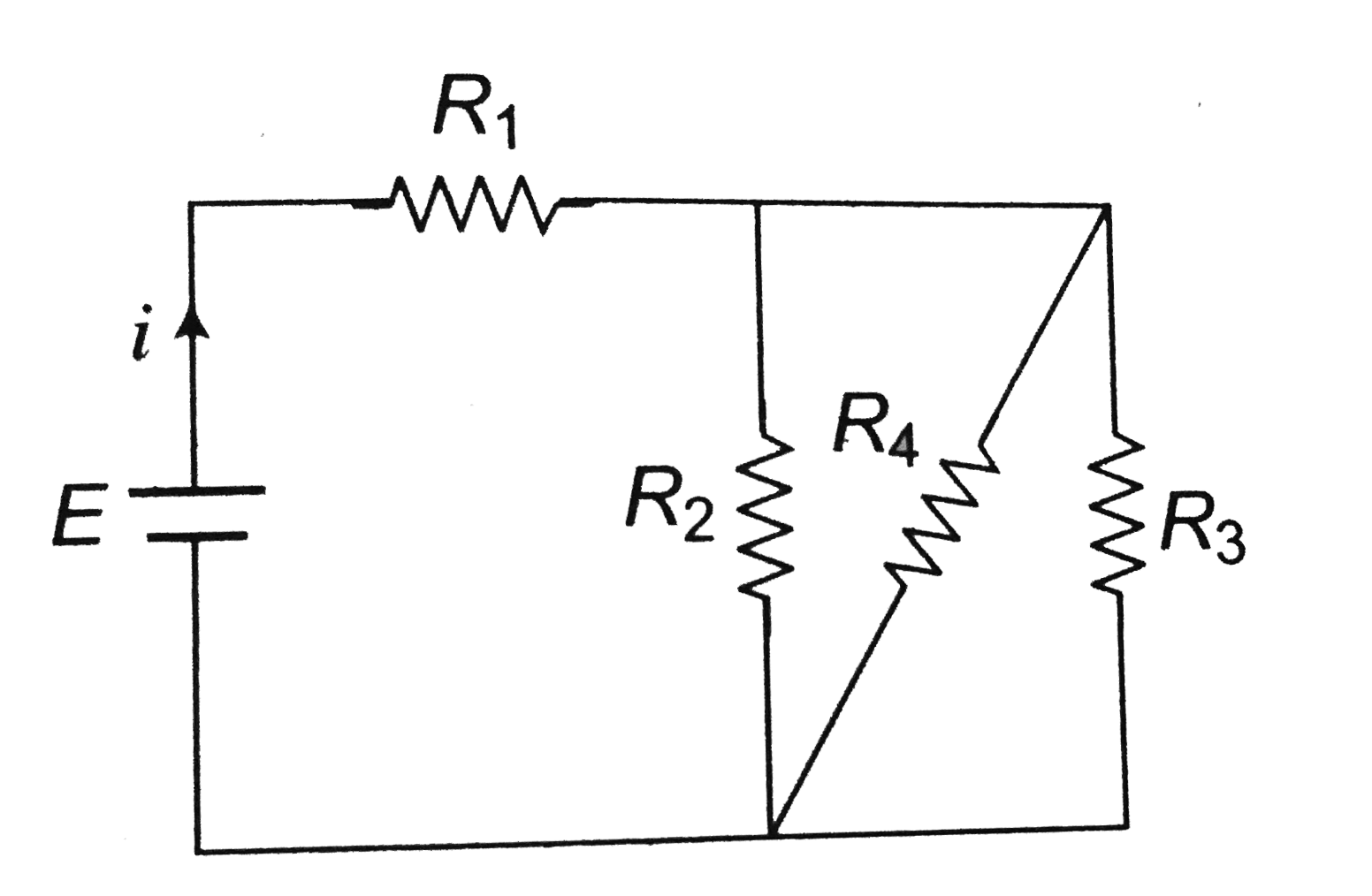 A11.875B26.31C118.75DNone of these
A11.875B26.31C118.75DNone of theseIn Fig, E=5 volt , r=1Ω,R2=4Ω,R1=R3=1Ω and C=3μF. Then the numbercal value of the charge on each plate of the capacitor is
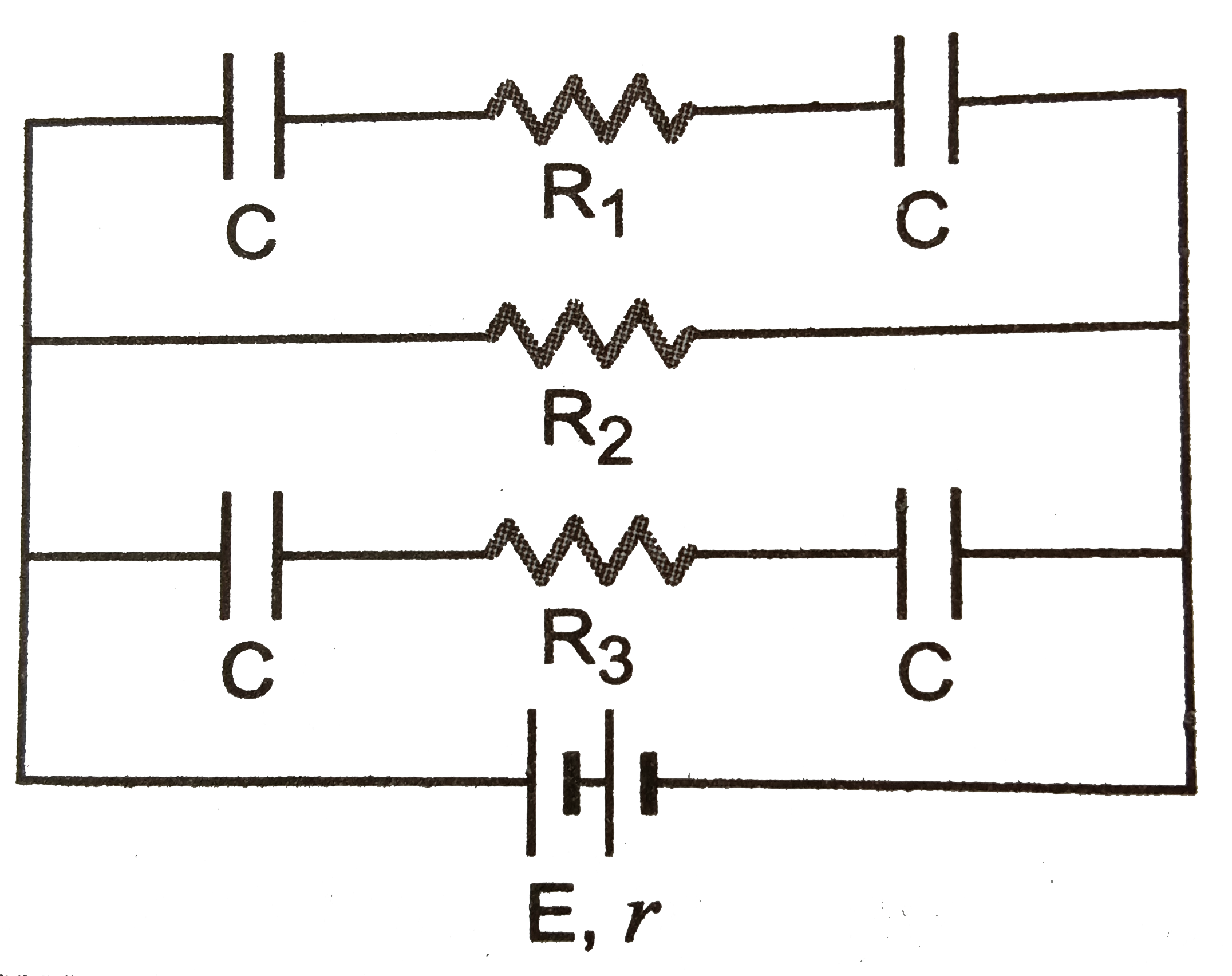 A24μCB12μCC6μCD3μC
A24μCB12μCC6μCD3μC
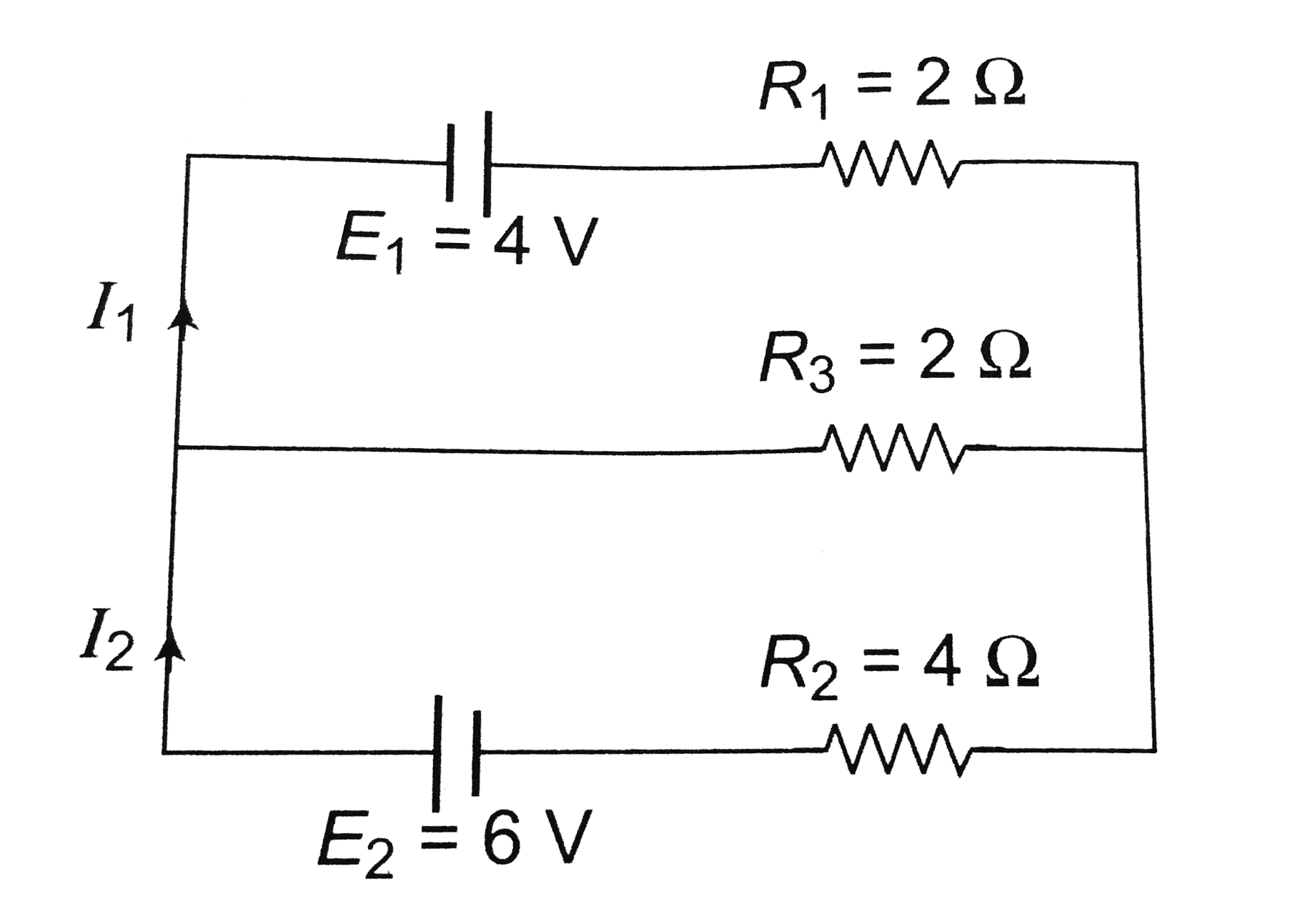
In the following circuit ,E1=4V,R1=2Ω,
E2=6V,R2=2Oemga,andR3=4Ω. Find the currents i1andi2
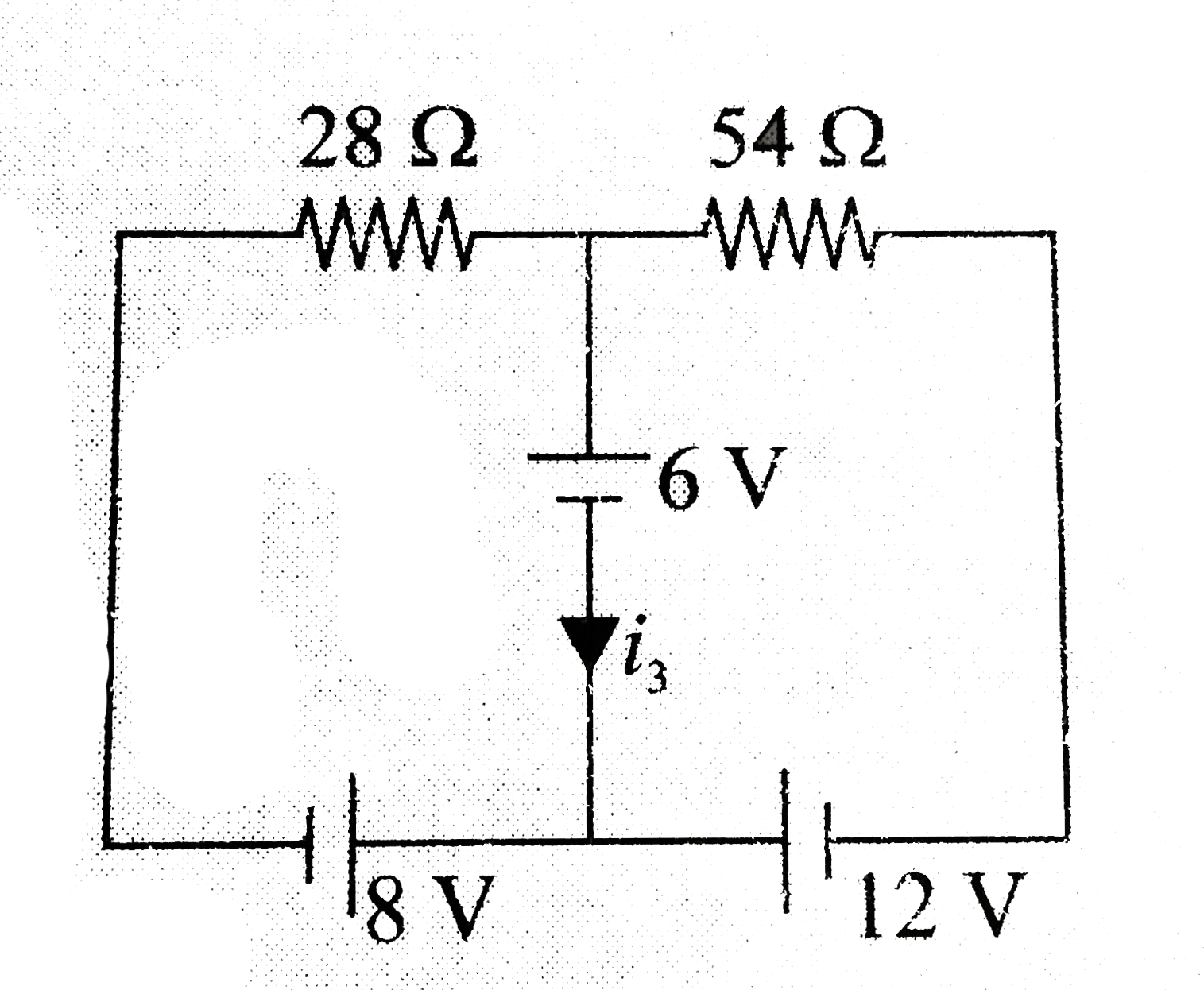
View SolutionIn the circuit shown in fig E1=3vo<s,E2=2vo<s,E3=1vo<andR=r1=r2=r3=1ohm.
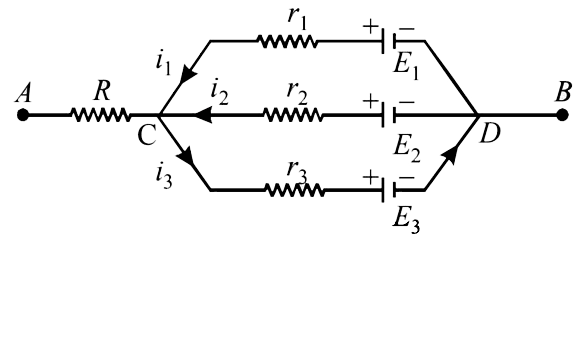
(i) Find the potential difference between the points A and B and the currents through each branch.
(ii) If r2 is short circuited and the point A is connected to point B, find the current through E1,E2,E3 and the resistor R.
View SolutionIn the circuit, E=10 volt, R1=5.0 ohm, R2=10ohm and L=5.0 henry. The current just after the switch S is pressed is.

View SolutionIn the circuit shown below E1=4.0V,R1=2Ω,E2=6.0V,R2=4Ω and R3=2Ω. The current I1 is
View SolutionIn the circuit shown in fig. 5.265, E1=E2=E3=2V and R1=R2=4Ω. The current flowing between points A and B through battery E2 is
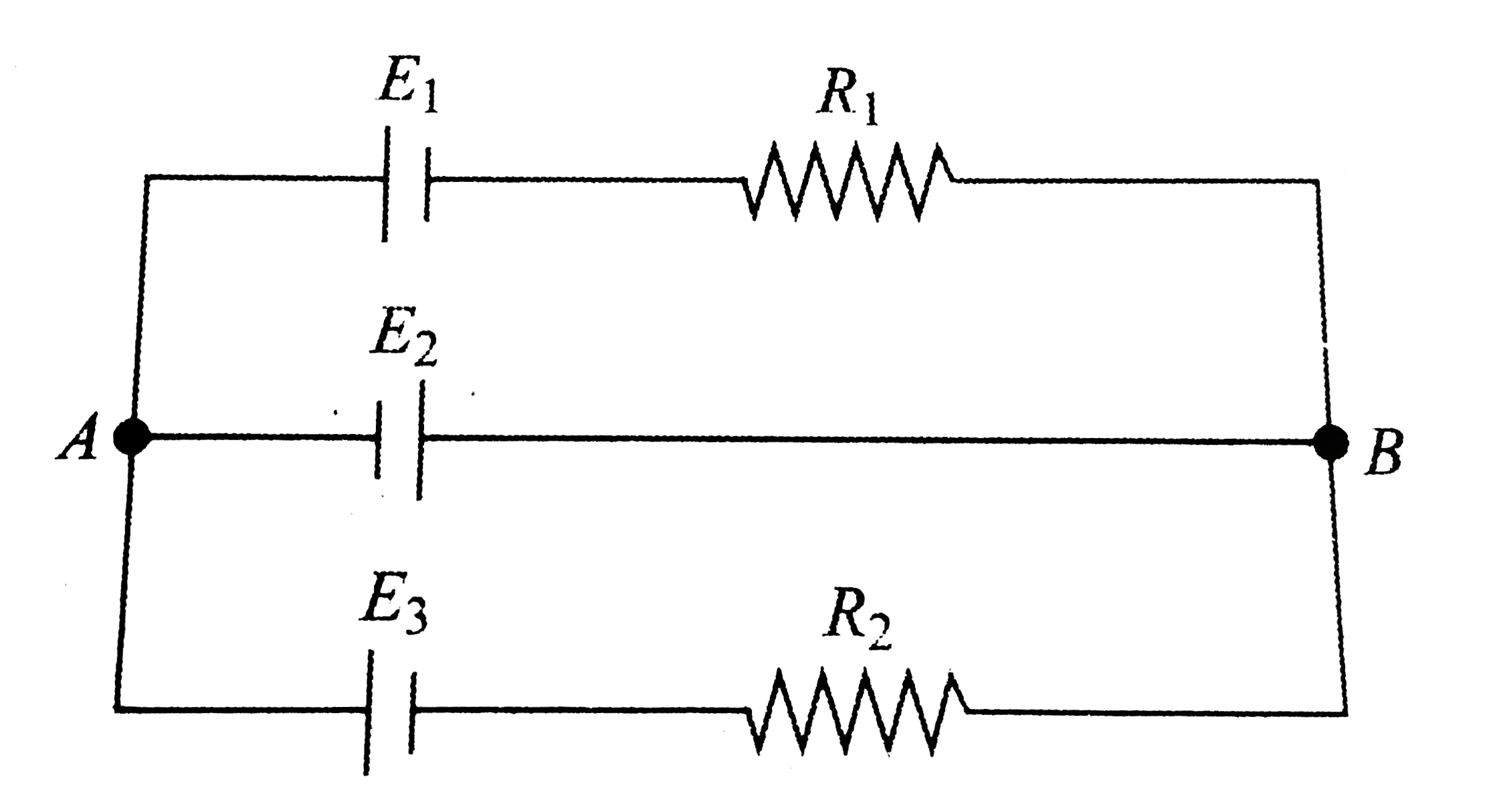
View Solution
