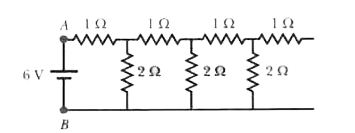
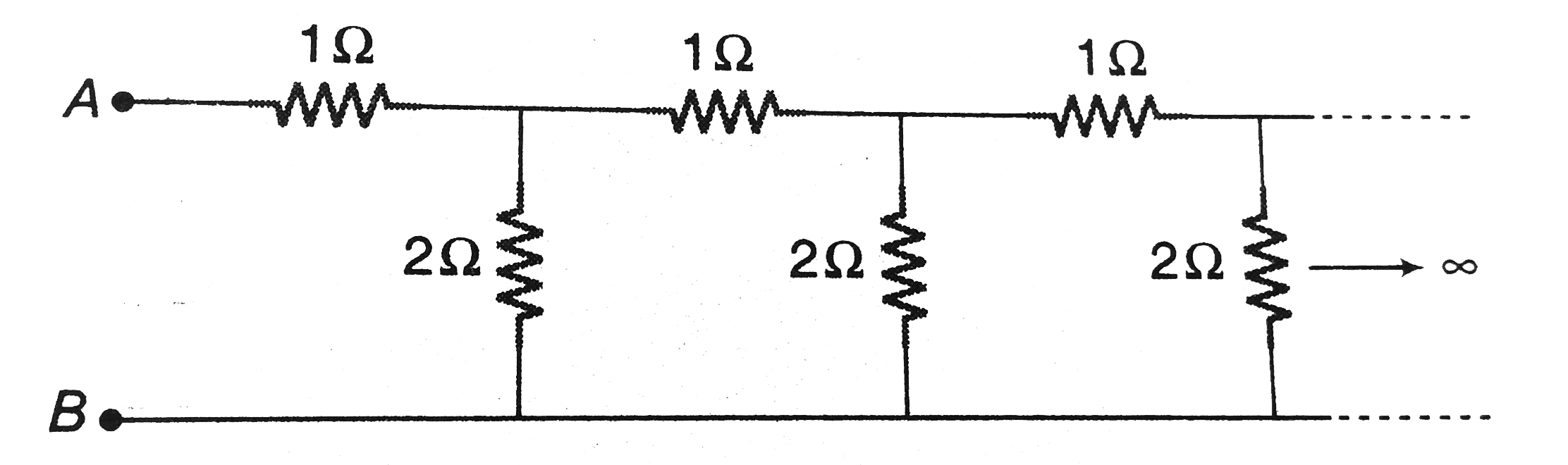
An infinite ladder is constructed with 1(Ω)and 2(Ω)resistor as shown in figure.(a)Find the effective resistance between the point A and B. (b) Find the current that passes through the (2Ω) resistor nearest to the battery.

Video Solution
Text Solution
The correct Answer is:A
(i) Let the effective resistance between points C and D be
R then the circuit can be redrawn as shown
The effective resistance between A and B is
Req=1+2×RR+2
 <br> This resistance <span class=) Req can be taken as R beacuse if we add one identical item to infinite items then the result will almost be
Req can be taken as R beacuse if we add one identical item to infinite items then the result will almost be
the same.
∴1+2×RR+2=R
⇒R+2+2R=R2+2R⇒R2−R−2=0
⇒R2−2R+R−2=0
⇒R(R−2)+1+(R2)=0
⇒[R+1][R−2]=0⇒R=2Ω.
(ii) RAB=1Ω+1Ω=2Ω∴IAB=62=3Amp.
Further, iCD=iCF as resistances RCD=RCF
∴iCD=iCF=1.5A .
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure shown the current through 2Ω resistor is
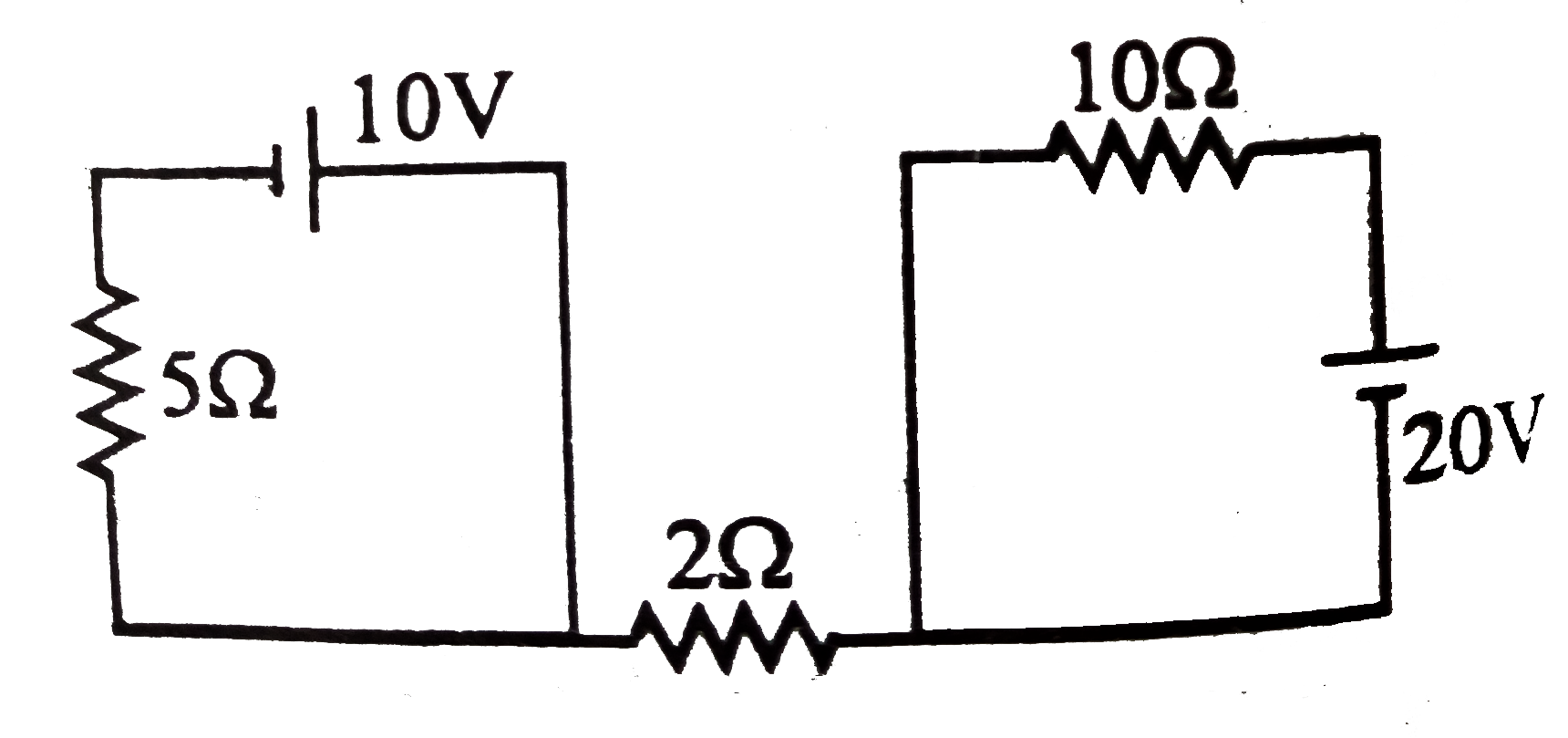 A2AB0AC4AD6A
A2AB0AC4AD6AIn the circuit shown in figure potential difference between point A and B is 16V. Find the current passing through 2Ω resistance.
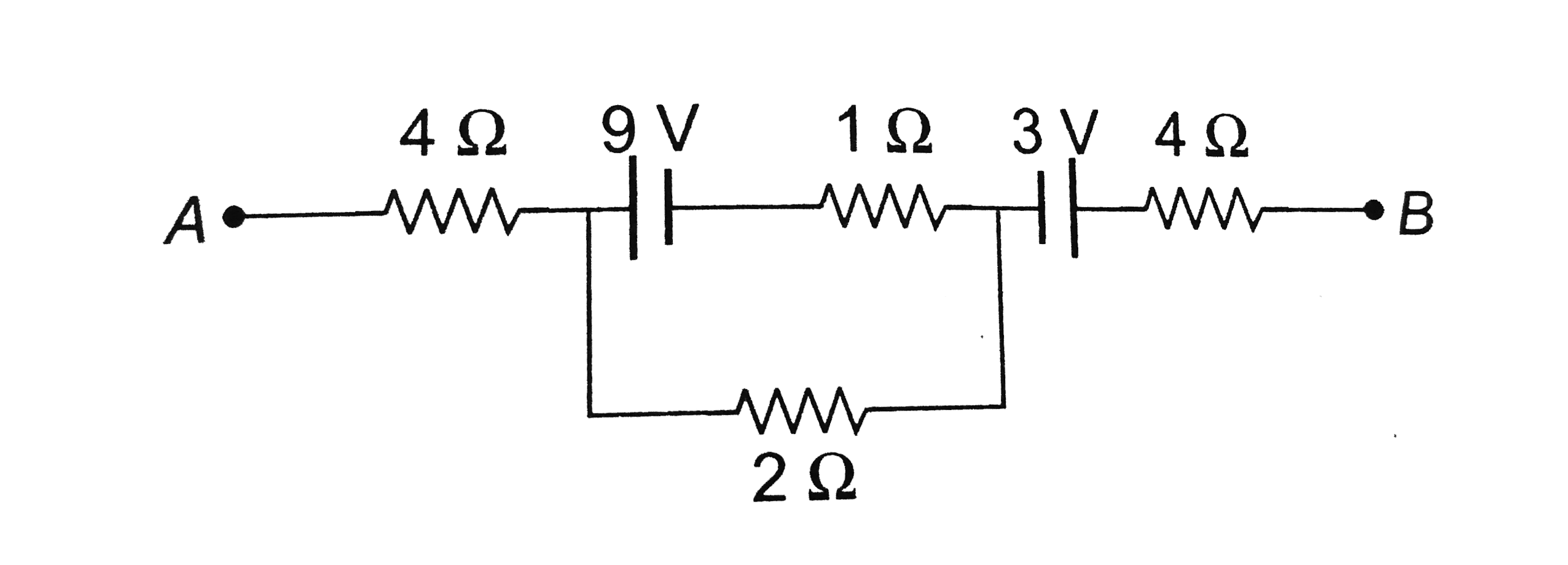 A1.5AB3.5AC1.0AD2.5A
A1.5AB3.5AC1.0AD2.5A
Find the current through the 10(Ω)resistor shown in figure.
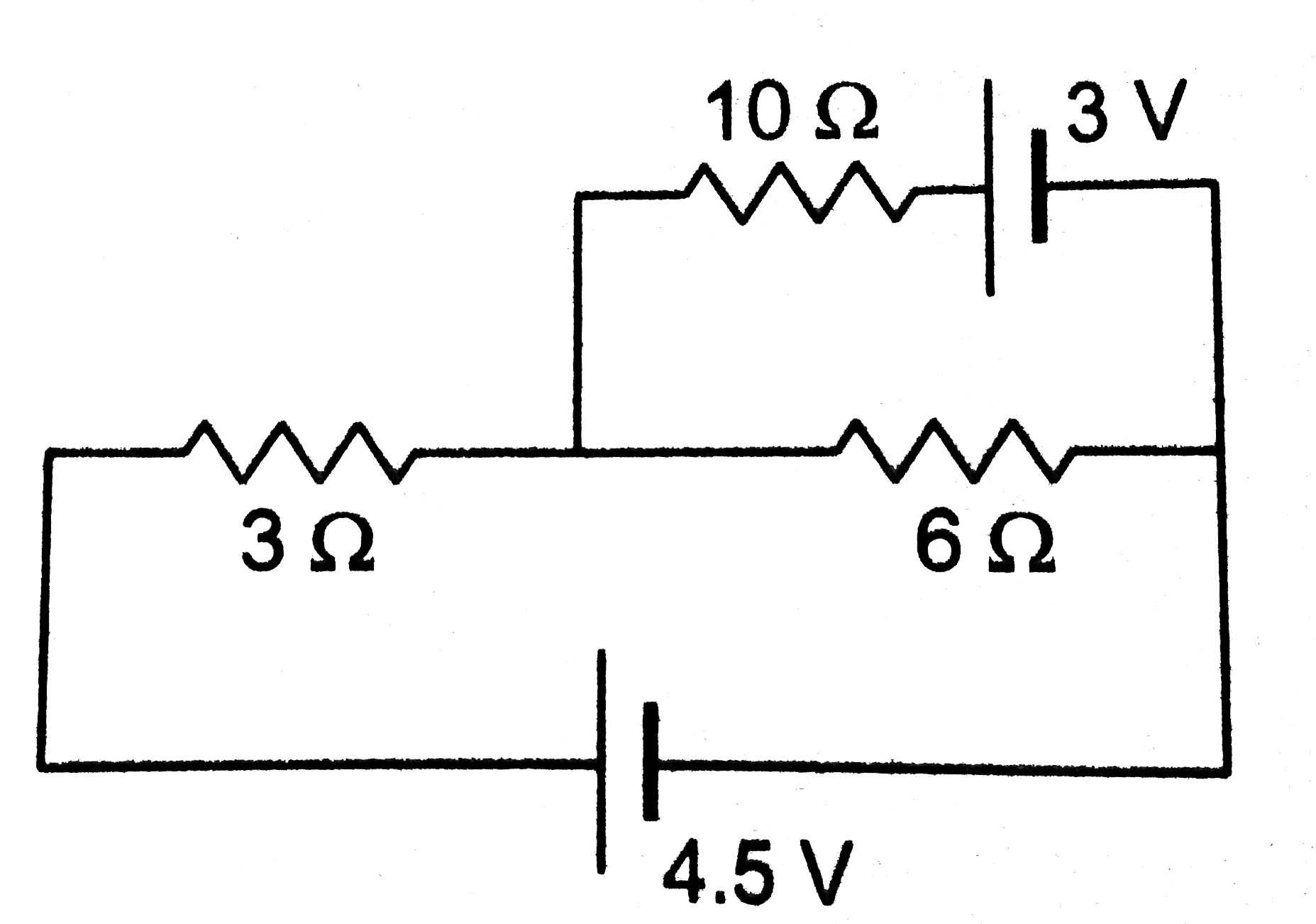
View SolutionFind the current through the 10Ω resistor shown in figure .
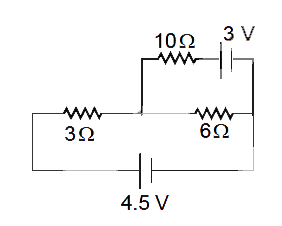
View Solution
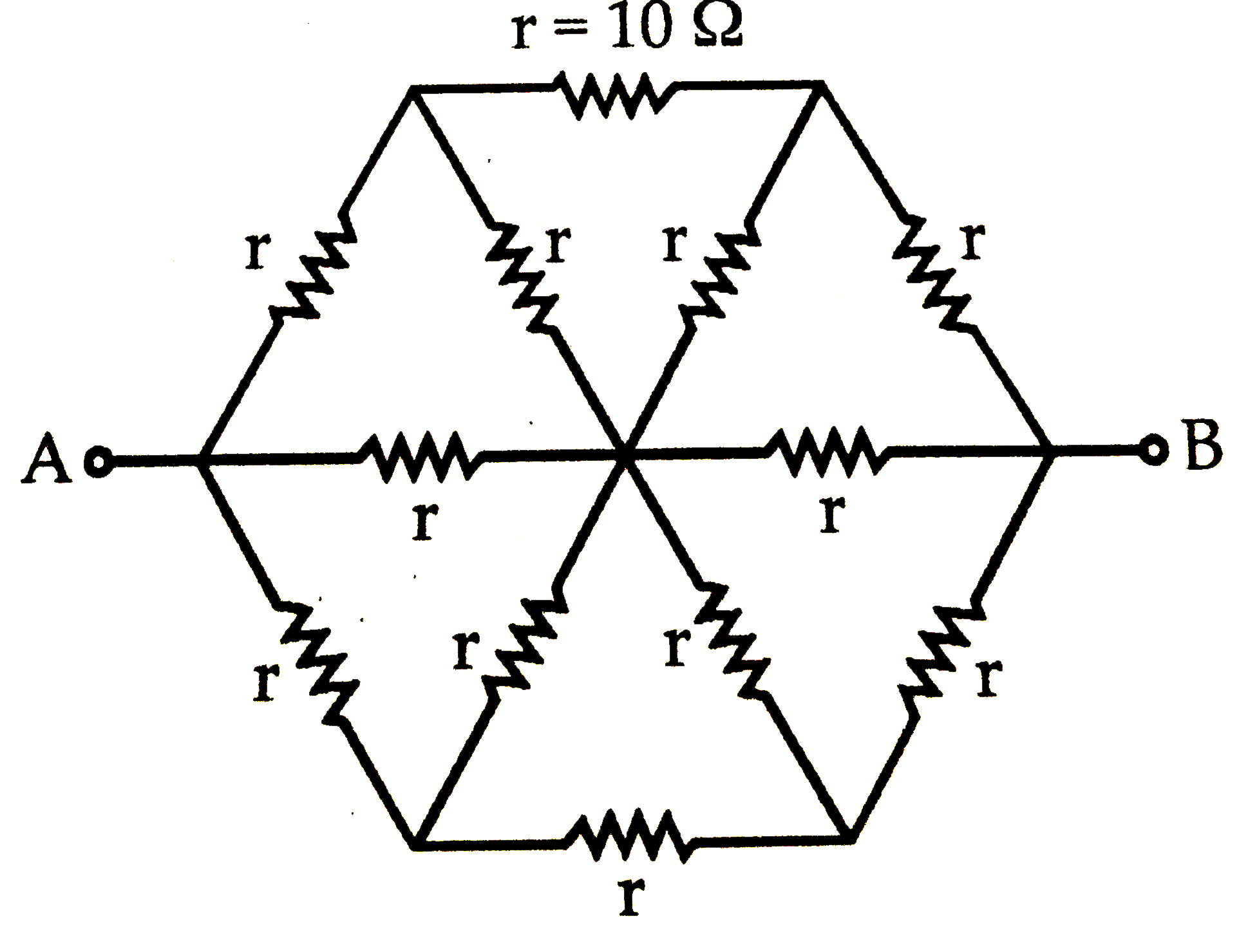
In the network as shown in figure. Each resistance r is of 2Ω find the effective resistance between points A and B.
View SolutionFind the current through 12Ω resistor in
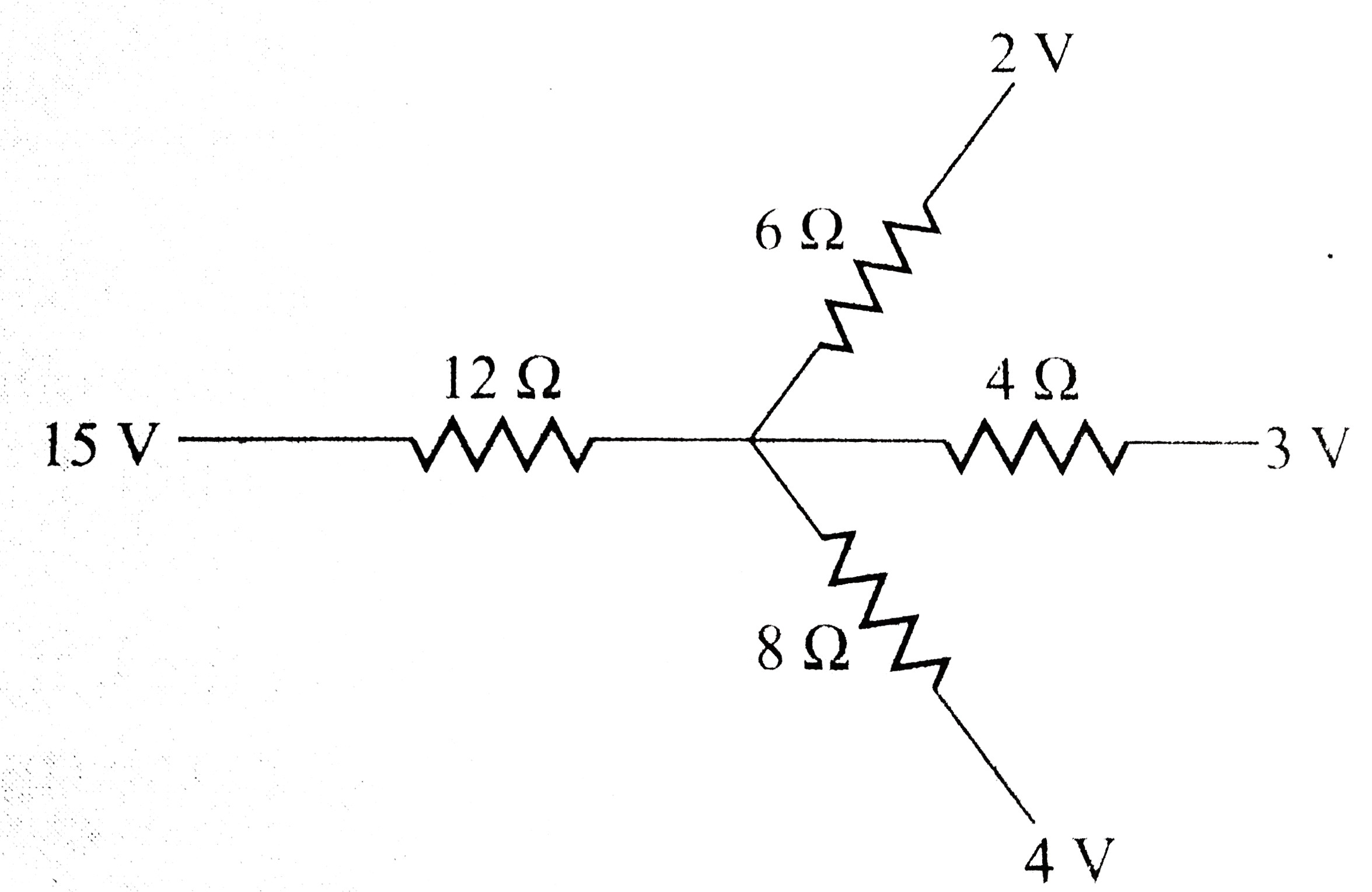
View SolutionFind the current through 23Ω resistance in the figure shown.
View Solution12 resistors each of 10Ω are connected as shown in the figure. The effective resistance between A and B is
View Solution