A spring is connected with plank and other end of spring is connected with a block of mass m. initially spring is stretched by a distance x0 and block is connected with a thread which is connected to other end of the plank as shown. If thread is cut, what will be maximum speed of the plank.

Take system: spring + plank + block
Observation for the system: No external force acts on the system in horizontal direction. Conclusion:

Both linear momentum and mechanical energy will be conserved for the system. Analysis of problem: The speed of the plank will be maximum when all the potential energy of spring converted into kinetic energy of system.
The initial linear momentum of system is zero and no external forces are acting on system, the linear momentum of the system be zero always.
The motion of the block and plank will be such that they will always move in opposite direction or both will be at rest to justify conservation of linear momentum.
Let speed of block and plank (at maximum case) be v and V respectively. Using conservation of linear momentum at this situation
mv=MV..............i
Now applying conservation of mechanicals energy
△K+△U=0
[(12MV2+12mv2)−0][0−12kx20]=0....................ii
from eq v=MVm
Substituting this value in eqn ii we get
[12MV2+12m(MV2m)2]=12kx20
⇒12[M+M2m]v2=12kx20
V2=kmx20(M2+Mm)⇒V=√kmM(M+m).x0
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.1
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.2
23 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
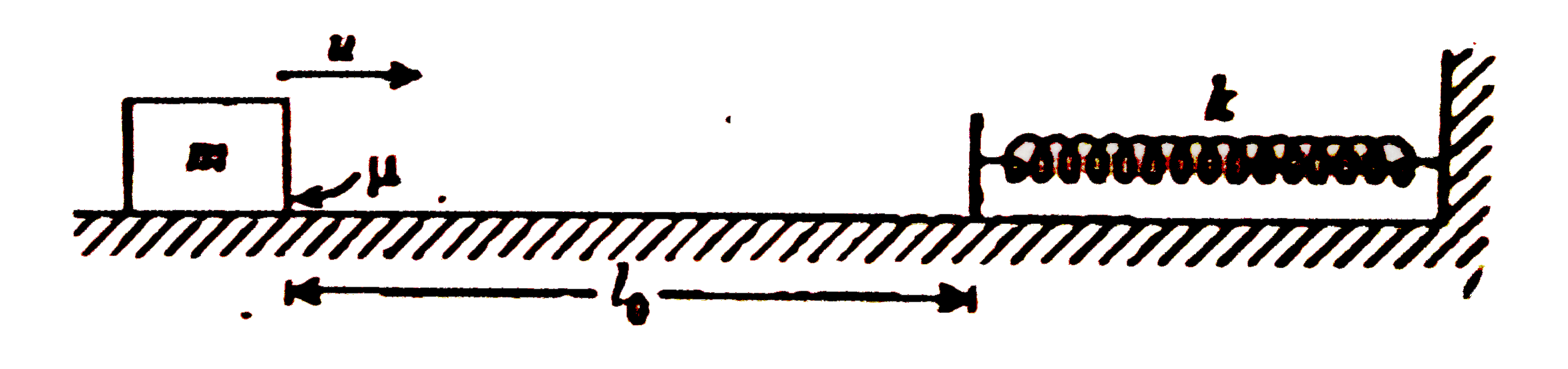
Figure. shows a rough horizontal plane which ends in a vertical wall, to which a spring is connected, having a force constant k. Initially spring is in its relaxed state. A block of mass m starts with an initial velocity u towards the spring from a distance l0 from the end of spring shown. When block strikes at the end ofthe spring, it compresses the spring and comes to rest. Find the maximum compression in the spring. The friction coefficient between the block and the floor is μ..
View SolutionTwo blocks of masses m and 2m compress a spring of spring constant k by x0 and blocks are a connected by a thread and placed on a smooth surface as shown. Now , thread is burned. Find the speed of each block when the spring attains its normal length L.
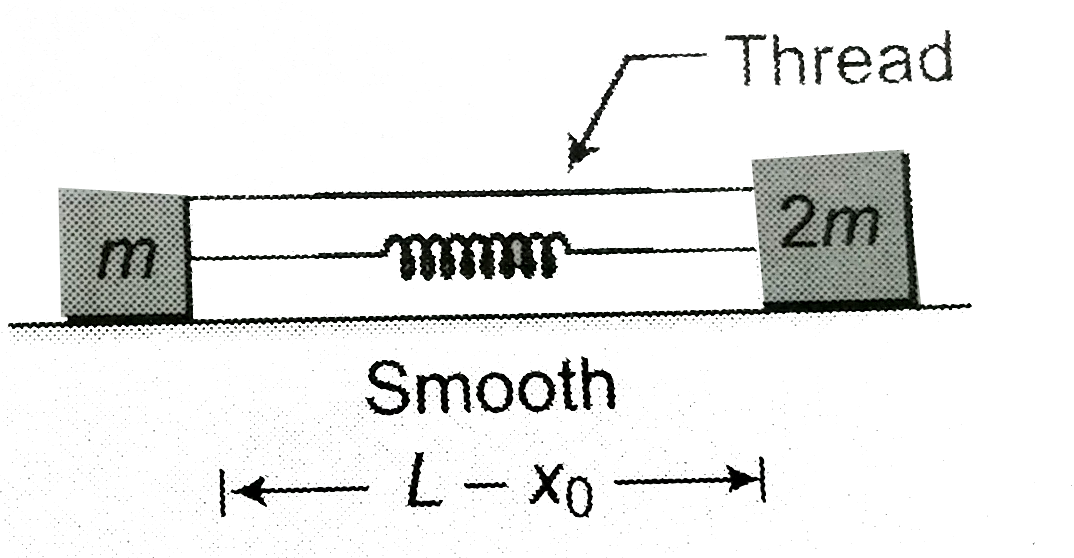
View Solution
Knowledge Check
According to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass M is placed on a smooth horizontal surface. light identical springs, each of stiffness K, are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is 3l. A block of mass m is placed on the plank and pressed against one of the springs so that it is compressed to l. To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.
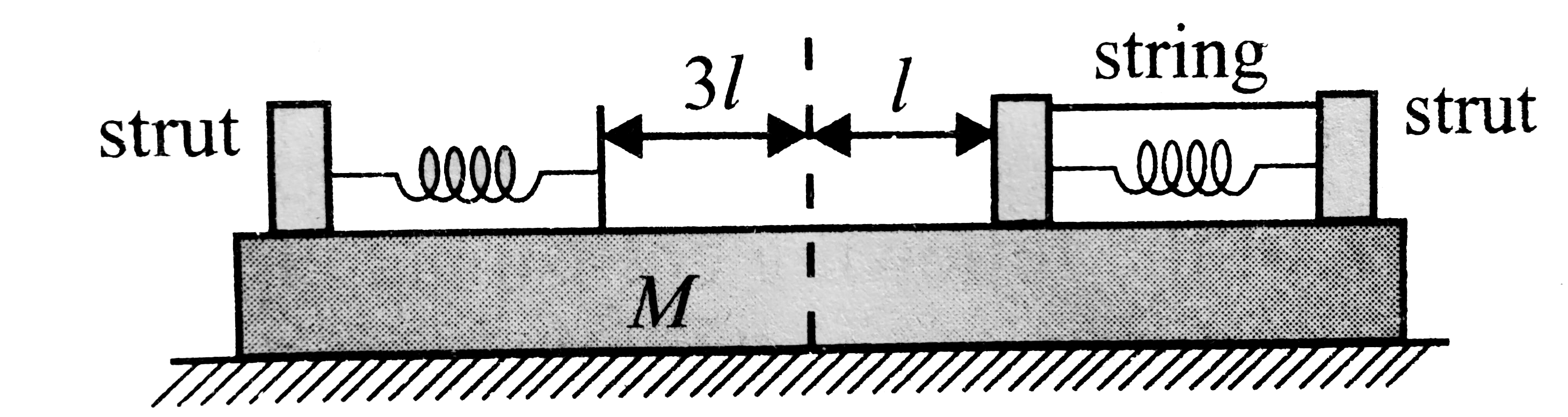
The maximum displacement of the plank isA5mlMB5mlM+mC3mlM+mD4mlM+mAccording to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass M is placed on a smooth horizontal surface. light identical springs, each of stiffness K, are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is 3l. A block of mass m is placed on the plank and pressed against one of the springs so that it is compressed to l. To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.

The maximum velocity of the plank isA√Km(M+m)lB√k(M+m)lC√KmM(M+m)lD√kMm(M+m)lOne end of an spring is connected with a smooth block with the other end with rear wall of a truck as shown in figure. initially, the system is at rest if track start to its accelerate with a constant acceleration then the block (relative to track)
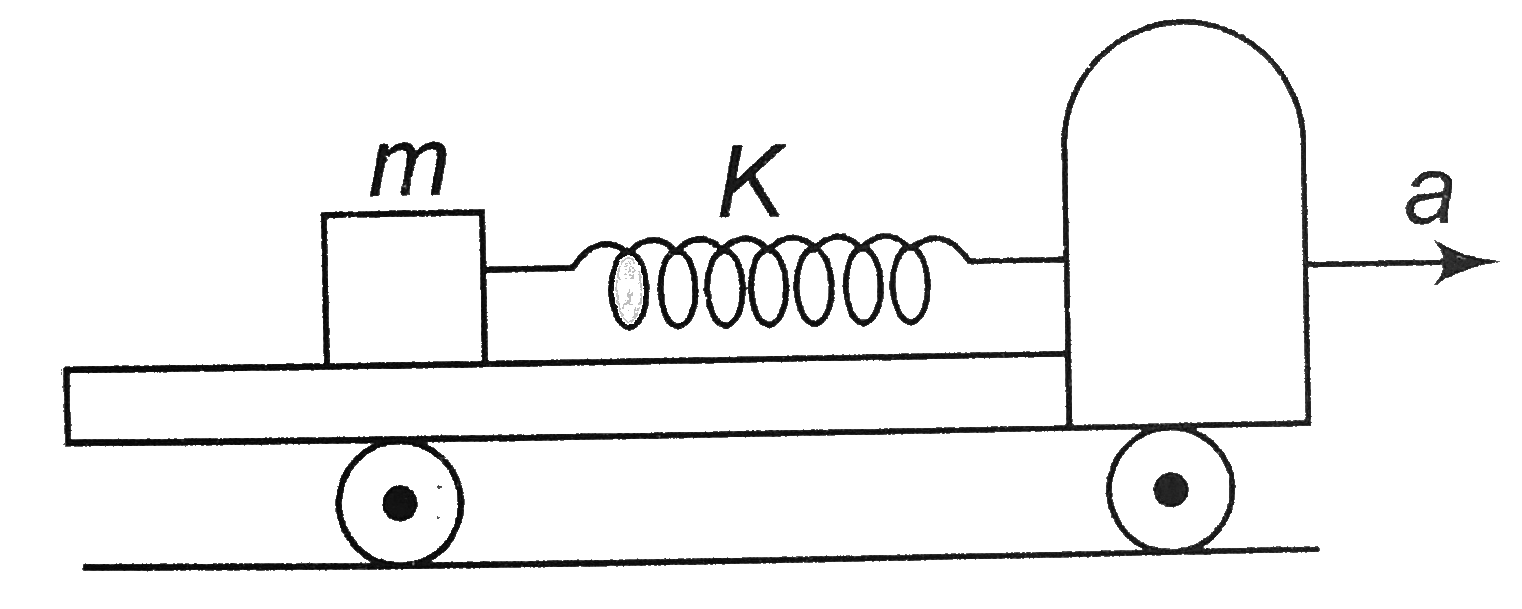 Awill remain stationary.Bwill start oscillation with constant amplitude.Cwill start stationary with increasing amplitude.Dmoves such that length of the spring first increases and then becomes constant.
Awill remain stationary.Bwill start oscillation with constant amplitude.Cwill start stationary with increasing amplitude.Dmoves such that length of the spring first increases and then becomes constant.
A block of mass m is connected rigidly with a smooth wedge (plank) by a light spring of stiffness k. If the wedge is moved with constant velocity v0, find the work done by the external agent till the maximum compression of the spring.
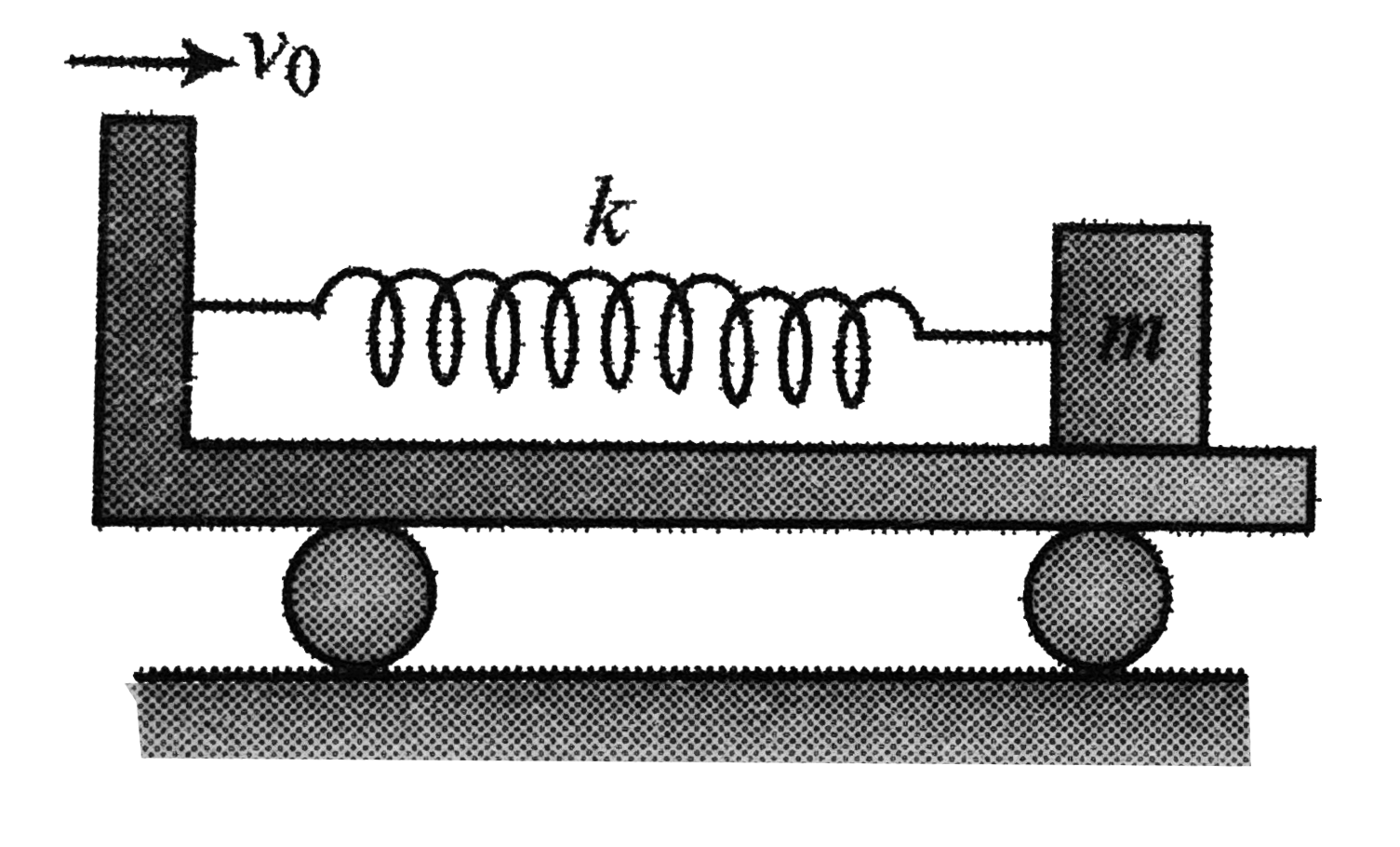
View SolutionA block of mass m is connected rigidly with a smooth wedge (plank) by a light spring of stiffness k. If the wedge is moved with constant velocity v0, find the work done by the external agent till the maximum compression of the spring.

View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionA block of mass m is connected to a massless pulley and mass-less spring of stiffness k. The pulley is frictionless. The string is mass-less. Initially the spring is unstretched when the block is released. When the spring is maximum stretched, find the ratio of tenstion in the rope and weight of the block.

View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View Solution
