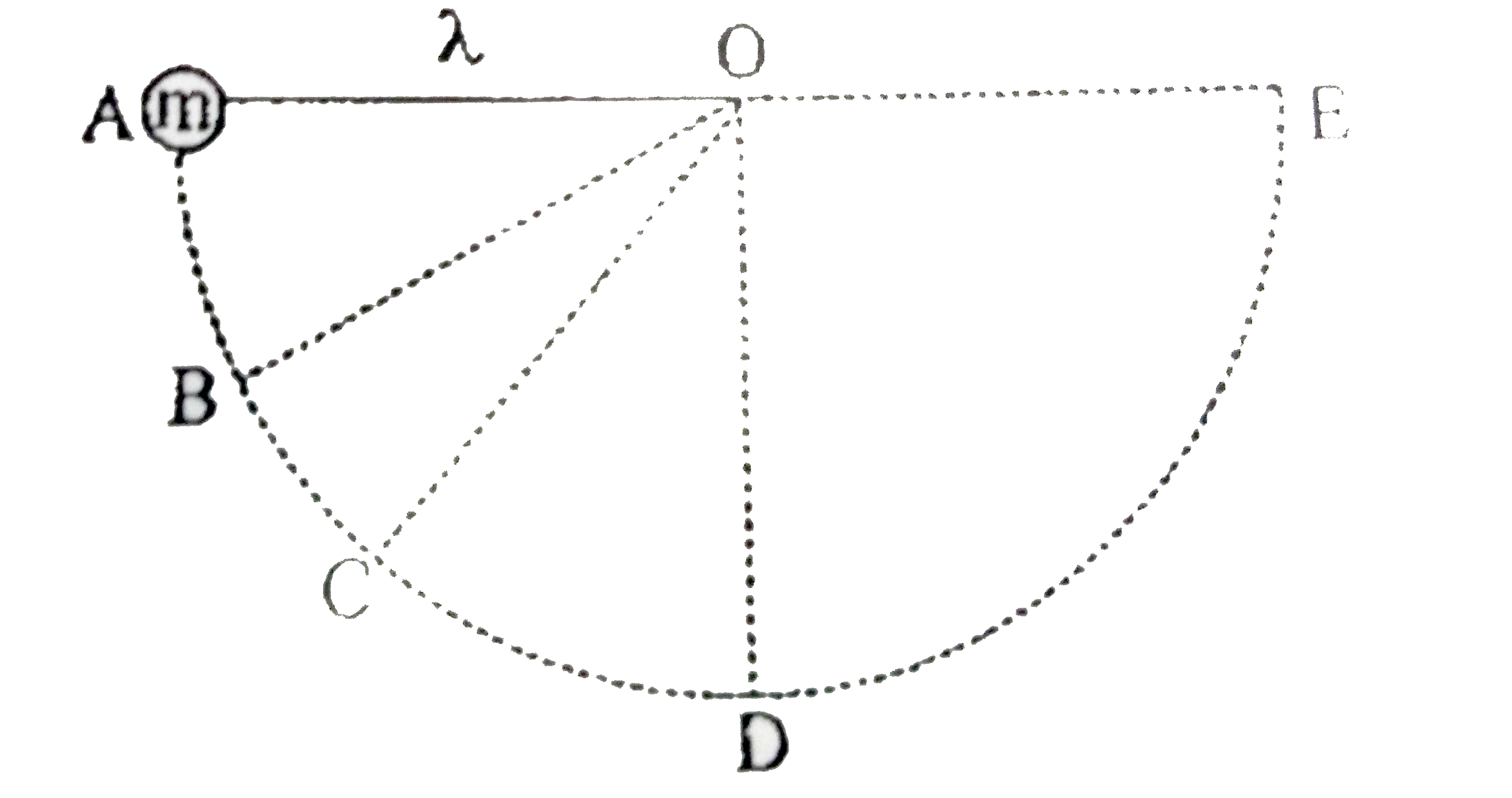
There are two pendulums with bobs having indencital size and mass. The pendulum $A$ is released from rest in the position as shown in the figure. If the maximum angle formed by cord $B O'$ with vertical in the subsequent motion of sphere $B$ is equal to the angle $θ_{0}$ If the coefficient of restitution between sphere $A$ and sphere $B$ is $l$ . find

a. the velocities of sphere $A$ and sphere $B$ just after collisions
b. the ratio of lengths of pendulums $l_{B} / l_{A}$ .

Text Solution

Verified by Experts

Velocity of $A$ just before collision
$v_{0} = \sqrt{2 g l_{A} (1 - {cos θ}_{A})}$ ………..i
Collision of $A$ and $B$
Using C.O.L.M. , $m . v_{0} + 0 = m v_{A} + m v_{B}$
$v_{A} + v_{B} = v_{0}$ ……ii
Using Newton's restitution law
$v_{B} - v_{A} = v_{0}$
$v_{B} - v_{A} = e v_{0}$ ………ii
Solving eqn i and ii $v_{A} = \frac{v_{0}}{2} (1 - e)$ and $v_{B} = \frac{v_{0}}{2} (1 + e)$
As $B$ swings angle $θ B$ , hence
$v_{B} = \sqrt{2 g h_{B} (1 - {cos θ}_{B})}$ ............iii
$and \frac{v_{0}}{2} (1 + e) = \sqrt{2 g l_{B} (1 - {cos θ}_{B})}$
$(\frac{2 g l_{A} (1 - {cos θ}_{A})}{2} (1 + e) \sqrt{2 g l_{B} (1 - {cos θ}_{B})}$
$\Rightarrow \frac{l_{B}}{l_{A}} = {(\frac{1 + e}{2})}^{2}$

Updated on:21/07/2023

A pendulum bob 'm' is released from rest from horizontal position as shown in the figure. ltbr> Choose the position where the chance of. Braking of the string is maximum.

AA
BB
CC
DD
A sphere impinges directly on an equal sphere at rest. If the coefficient of restitution is 1/2, then their velocities after the impact are in the ratio
A $1 : 2$
B $2 : 3$
C $1 : 3$
D $3 : 4$
A sphere impinges directly on an equal sphere at rest. If the coefficient of restitution is e, their velocities after the impact are as
A $1 : e$
B $e : 1$
C $1 + e : 1 - e$
D $1 - e : 1 + e$