A bead of mass m kept at the top of a smooth hemispherical wedge of mass M and radius R, is gently pushed towards right. As a result, the wedge slides due left Find the
a. speed of the wedge
b. magnitude of velocity of the beard relative to the wedge.

Applying work energy theorem

Wgravity=△K'+△KC…………..i
△K'= change in KE w.r.t centre of mass from and △KC= change in kinetic energy of centre of mass w.r.t ground.
Let v is the velocities of ball wilth respect to wedge and V is the velocity of wedge.
Linear mometum will be conserved in the horizontal direction . Hence MV=(vcosθ−V)
⇒V=mvcosθ(m+M) ...............ii
The velocity of centre of mas will be zero in horizontal direction but the velocity of centre of mass will change in vertical direction .
(vcm)y=mvsinθ(m+M) .............iii
Now applying WE theorem
−mgR(1−cosθ)=12μv2+12(m+M)v2cm,y
Here μ=mM(m+M) and vcm,y=mvsinθ(m+M)
which gives v=
⎷2(M+m)gR(1−cosθ)(M+Msin2θ)
and from eqn ii V=
⎷2m2gR(1−cosθ)cos2θ(M+m)(M+Msin2θ)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.1
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.2
23 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
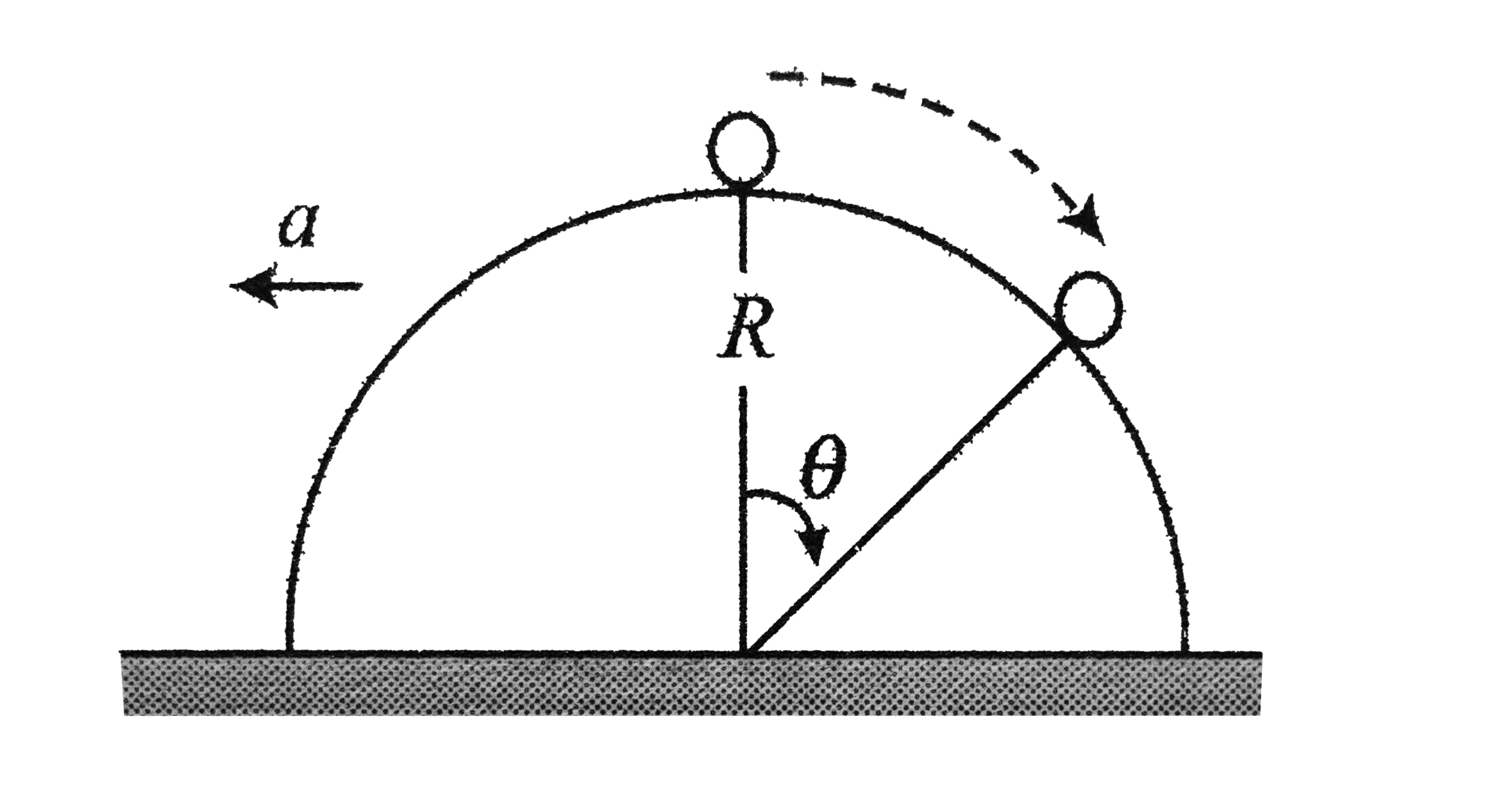
A small ball is placed at the top of a smooth hemispherical wedge of radius R. If the wedge is accelerated with an acceleration a, find the velocity of the ball relative to wedge as a function of θ.
View SolutionA particle of mass m is released from rest from a point A of a wedge of mass 4m free to slide on a frictionless horizontal plane.The particle slides down the smooth face AB of the wedge.When the velocity of the wedge is 0.2m/s the velocity of the particle in m/s relative to the wedge is
View Solution
Knowledge Check
A small ball is placed at the top of a smooth hemispherical wedge of radius R. If the wedge is accelerated with an acceleration a, find the velocity of the ball relative to wedge as a function of θ.
 A√2R[g(1−sinθ)+aRcosθ]B√2R[g(1+cosθ)−aRsinθ]C√2R[g(1−cosθ)+aRsinθ]D√2R[g(1+sinθ)−aRcosθ]
A√2R[g(1−sinθ)+aRcosθ]B√2R[g(1+cosθ)−aRsinθ]C√2R[g(1−cosθ)+aRsinθ]D√2R[g(1+sinθ)−aRcosθ]All surfaces are smooth The acceleration of mass m relative to the wedge is
 .AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ
.AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ
A particle of mass m is released from rest from a point A of a wedge of mass 4m free to slide on a frictionless horizontal plane. The particle slides down the smooth face AB of the wedge. When the velocity of the wedge is 0.2 m/s the velocity of the particle in m/s relative to the wedge is
View SolutionA particle of mass m is released from rest from a point A of a wedge of mass 4m free to slide on a frictionless horizontal plane. The particle slides down the smooth face AB of the wedge. When the velocity of the wedge is 0.2 m/s the velocity of the particle in m/s relative to the wedge is
View SolutionA particle of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. Then the distance moved by the wedge as the particle reaches the foot of the wedge is :
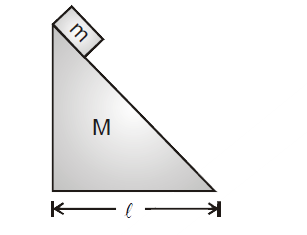
View SolutionA particle of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. Then the distance moved by the wedge as the particle reaches the foot of the wedge is :

View SolutionA wedge of mass M rests with one face in contact with horizontal , smooth surface . A particle of mass m is placed on the smooth face on it , inclined at an angle αto the horizontal and released . Find the velocity of the wedge and that of the particle relative to the wedge when the particle has slipped a distance x down the face of the wedge . Also calculate the acceleration of the wedge and that of the particle relative to the wedge and the smooth surface .
[Hint : Apply principal of conservation of momentum along the horizontal and energy conservation principle . See Example 8 )
View SolutionA block of mass 'm' is kept on a smooth moving wedge. If the acceleration of the wedge is 'a'
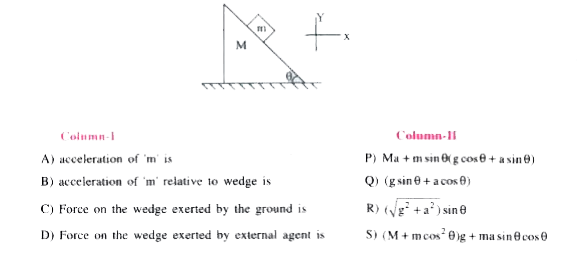
View Solution
