In a fig. PA is a tangent to the circle. PBC is a secant & AD bisects angle BAC. Show that triangle PAD is an isosceles triangle.Also show that ∠CAD=12(∠PBA−∠PAB)
Step by step video & image solution for In a fig. PA is a tangent to the circle. PBC is a secant & AD bisects angle BAC. Show that triangle PAD is an isosceles triangle.Also show that /_CAD=1/2(/_PBA-/_PAB) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
In the figure PA is a tangent to the circle, PBC is secant and AD bisects angle BAC.
Show that triangle PAD is an isosceles triangle. Also, show that:
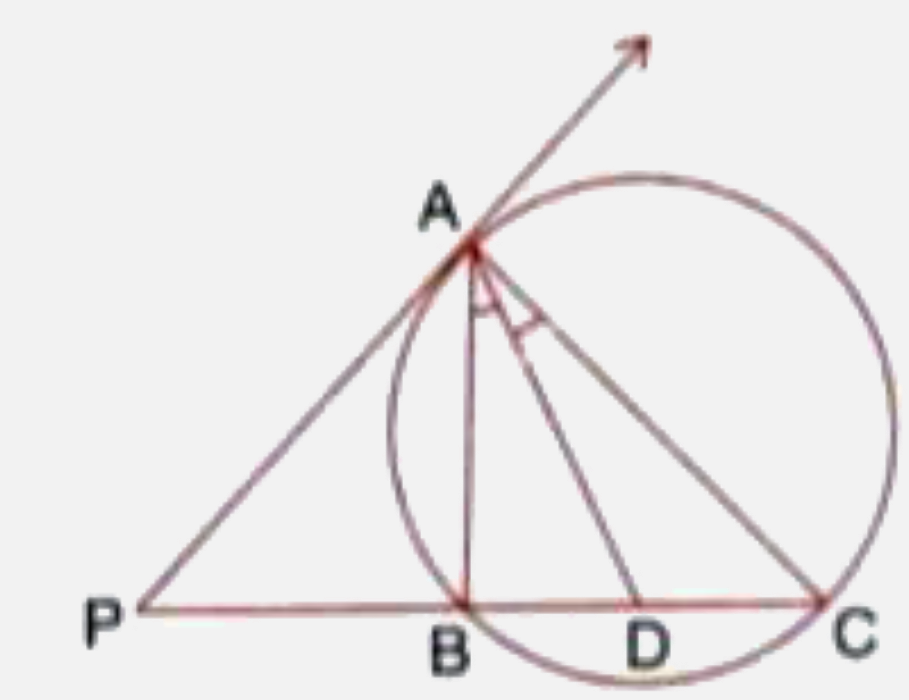
∠CAD=12[∠PBA−∠PAB]
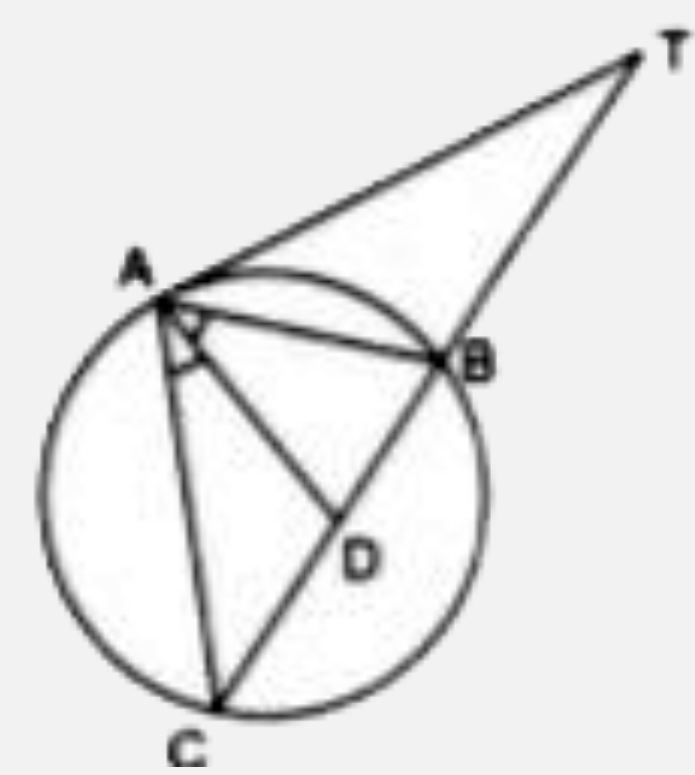
View SolutionIn the given TA is a tangent to the cirlce and TBC is a secant. If AD bisects angle BAC, prove that:ΔADT is isosceles.
View SolutionIn the figure, AB is a diameter PA is a tangent to the circle and PCB is a secant. Show that △ABP~△CAP
View SolutionIn Fig. 10.64, BC is a tangent to the circle with centre O.OE bisects AP. Prove that ΔABC~ΔAEO
View SolutionAs shown in the figure, PA is a tangent to a circle and PBC is a secant, so that PB = AB. Prove that PB.PC=AC2
View SolutionIn a triangle ABC, side AC is greater than side AB and point D lies on side BC such that AD bisects angle BAC. Show that:
∠ADB is acute.
View SolutionInΔABC,AB=ACandD is a piont in side BC such that AD bisect angle BAC.
Show that AD is perpendicular bisector of side BC.
View SolutionIn the figure, ∠D=∠EandADDB=AEEC, prove that ΔBAC is an isosceles triangle
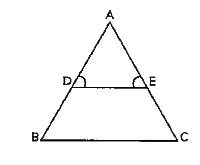
View SolutionShow that the right triangle of maximum area that can be inscribed in a circle is an isosceles triangle
View SolutionIn the figure, ∠D=∠E and ADDB=AEEC, prove that BAC is an isosceles triangle.

View Solution
