चित्र 14.49 में ABCD एक समद्विबाहु त्रिभुज है जिसमे AB=AC,CP∣∣AB तथा ΔABC के बहिष्कोण ∠CAD का अर्धक AP है। सिद्ध कीजिए की ∠PAC=∠BCA(ii)ABCP एक समान्तर चतुभुर्ज है ।
दिया है : समद्विबाहु ΔABC जिसमे AB=AC तथा बहिष्कोण ∠CAD का अर्धक AP इस प्रकार है की CP∣∣AB
सिद्ध करना है : ∠PAC=∠BCA तथा ABCD एक समान्तर चतुभुर्ज है।
उपपत्ति ΔABC में
AB=AC [दिया है]
⇒∠1=∠2 [∴Δ में बराबर भुजाओं के सम्मुख कोण बराबर होते है]
पुनः ΔABC में
बहिष्कोण ∠CA=∠1+∠2 [ ∴ बहिष्कोण अपने सम्मुख कोणों के योगफल के बराबर होता है]
⇒ बहिष्कोण ∠CAD=2∠2 [∴∠1=∠2(i) से]
⇒2∠3=2∠2[∴AP बहिष्कोण ∠CAD का अर्धक है : ∠CAD=2∠3]
⇒∠3=∠2
अतः रेखा AC रेखाओं AP तथा BC को क्रमशः A तथा C पर इस प्रकार प्रतिच्छेदित करती है, ∠3=∠2 अथार्त एकान्तर अन्तः कोण बराबर है।
∴AP∣∣BC
परन्तु CP∣∣AB [ दिया है]
अतः ABCP एक चतुभुर्ज इस प्रकार का है,की AP∣∣BC तथा CP∣∣AB
इसलिए ABCP एक समान्तर चतुर्भुर्ज है।
Topper's Solved these Questions
- BOOK - RD SHARMACHAPTER - चतुभुर्ज EXERCISE - प्रश्नावली 14.14videos
चतुभुर्ज
- BOOK - RD SHARMACHAPTER - चतुभुर्ज EXERCISE - प्रश्नावली 14.216videos
चतुभुर्ज
- BOOK - RD SHARMACHAPTER - घनाभ और घन का पृष्ठीय क्षेत्रफल तथा आयतन EXERCISE - बहु विकल्पीय प्रश्न22videos
घनाभ और घन का पृष्ठीय क्षेत्रफल तथा आयतन
- BOOK - RD SHARMACHAPTER - त्रिभुज तथा उसके कोण EXERCISE - बहु विकल्पीय प्रश्न28videos
त्रिभुज तथा उसके कोण
Similar Questions
एक चतुभुर्ज है तीन कोण क्रमशः 110∘,50∘ तथा 40∘ है। इसका चौथा कोण ज्ञात कीजिए।
View Solutionएक समान्तर चतुर्भुज के दो सम्मुख कोण (3x−2)∘ तथा (50−x)∘ है। समान्तर चतुभुर्ज के प्रत्येक कोण की माप ज्ञात कीजिए?
03:09View Solutionयदि किसी घनाभ के तीन आसन्न फलकों के क्षेत्रफल A1,A2 व A3 से दर्शाया जावे तो इस घनाभ का आयतन होगा :
02:25View Solutionयदि किसी त्रिभुज के तीनो कोण बराबर हो, तो प्रत्येक कोण का माप होगा:
04:05View Solutionसंलग्न चित्र में ABC एक समद्विबाहु है जिसमे AB=AC,CP∣∣AB तथा AB के AP,ΔABC बाहय कोण ∠CAD का अर्द्धक है सिद्ध कीजिए की
(i)∠PAC=∠BCA
(ii) ABCP एक समान्तर चतुर्भुर्ज है।05:06View Solutionएक ΔABC में, AB = ri + j, AC =si-j, यदि त्रिभुज का क्षेत्रफल इकाई परिमाण का है। तब,
04:28View SolutionABCD is a rectangle P is point on the side AB as shown in the given figure. If DP = 13, CP = 10 and BP = 6, then what is the value of AP?
ABCD एक आयत है। P, भुजा AB पर एक बिन्दु है जैसा की दी गई आकृति में दर्शाया गया है। यदि DP = 13, CP = 10 तथा BP = 6 हो, तो AP का मान क्या है?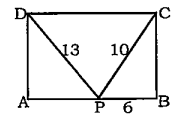
04:56View SolutionABC is a triangle. AB =10cm and BC=16 cm AD=8 cm and is perpendicular to side BC. What is the length (in cm) of side AC? ABC एक त्रिभुज है। AB =10 सेमी तथा BC=16 सेमी है। AD=8 सेमी है तथा यह भुजा BC के समलम्ब है। भुजा AC का मान (सेमी. में) क्या है?
04:26View SolutionIn triangle ABC, DE||BC where D is a point on AB and E is a point on AC. DE divides the area of triangle ABC into two equal parts.Then DB : AB is equal to एक त्रिभुज ABC DE||BC है जिसमें D,AB पर एक बिंदू है और E, AC पर एक बिंदू है। DE, triangle ABC के क्षेत्रफल को दो समान भागों में विभाजित करता है, DB : AB किसके बराबर हे?
02:26View SolutionIn an isosceles triangle ABC, AB=AC and AD is perpendicular to BC at D. If AD = 8 cm and perimeter of triangle ABC is 64cm, then the area of triangle ABC एक समद्विबाहु त्रिभुज ABC में, AB= AC और AD, BC पर लंबवत है। यदि AD =8 सेमी और ABC की परिधि 64 cm है, तो ABC का क्षेत्रफल है:
01:53View SolutionIn a triangle ABC, AB =AC and the perimeter of A ABC is 8(2 + sqrt 2) cm . If the length of BC is sqrt 2 times the length of AB, then find the area of triangle ABC . एक त्रिभुज ABC में AB = AC और triangle ABC की परिधि 8(2 + sqrt 2) सेमी है। यदि 80 की लंबाई AB की लंबाई से sqrt 2 गुना है, तो triangle ABC का क्षेत्रफल ज्ञात कीजिए|
03:50View SolutionA circle is inscribed in triangle ABC , touching AB at P, BC at Q and AC at R. If AR=5 cm, RC= 6 cm and AB=12 cm, then perimeter of triangle ABC is: एक वृत्त किसी त्रिभुज ABC में समाहित है जो AB को P पर, BC को Q पर तथा AC को R पर स्पर्श करता है | यदि AR =5 सेमी और AB = 12 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |
05:17View SolutionIn triangle ABC , D is a point on AC such that AB = BD = DC. If angle BAD=70^@ , then the measure of angle B is: त्रिभुज ABC में, D एक ऐसा बिंदु है कि AB = BD = DC है । यदि angle BAD=70^@ है, तो कोण B का मान ज्ञात करें |
02:08View SolutionIn triangle ABC, the length of BC is less than twice the length of AB by 2 cm. The length of AC exceeds the length of AB by 10 cm. The perimeter is 32 cm. The length (in cm) of the smallest side of the triangle is :
त्रिभुज ABC में, BC की लंबाई AB की लंबाई के दोगुने से 2 कम है | AC की लंबाई AB की लंबाई से 10 सेमी अधिक है | परिमाप 32 सेमी है | त्रिभुज की सबसे छोटी भुजा की लंबाई है -00:54View SolutionIn angle ABC , AB=AC . A circle drawn through B touches AC at D and intersects AB at P. If D is the mid point of AC and AP = 2.5 cm, then AB is equal to: त्रिभुज ABC में, AB = AC है | B से खींचा गया एक वृत्त AC को D पर स्पर्श करता है तथा AB को P पर काटता है | यदि D, AC का मध्य बिंदु है एवं AP = 2.5 सेमी है, तो AB का मान किसके बराबर है ?
01:57View Solution