Question

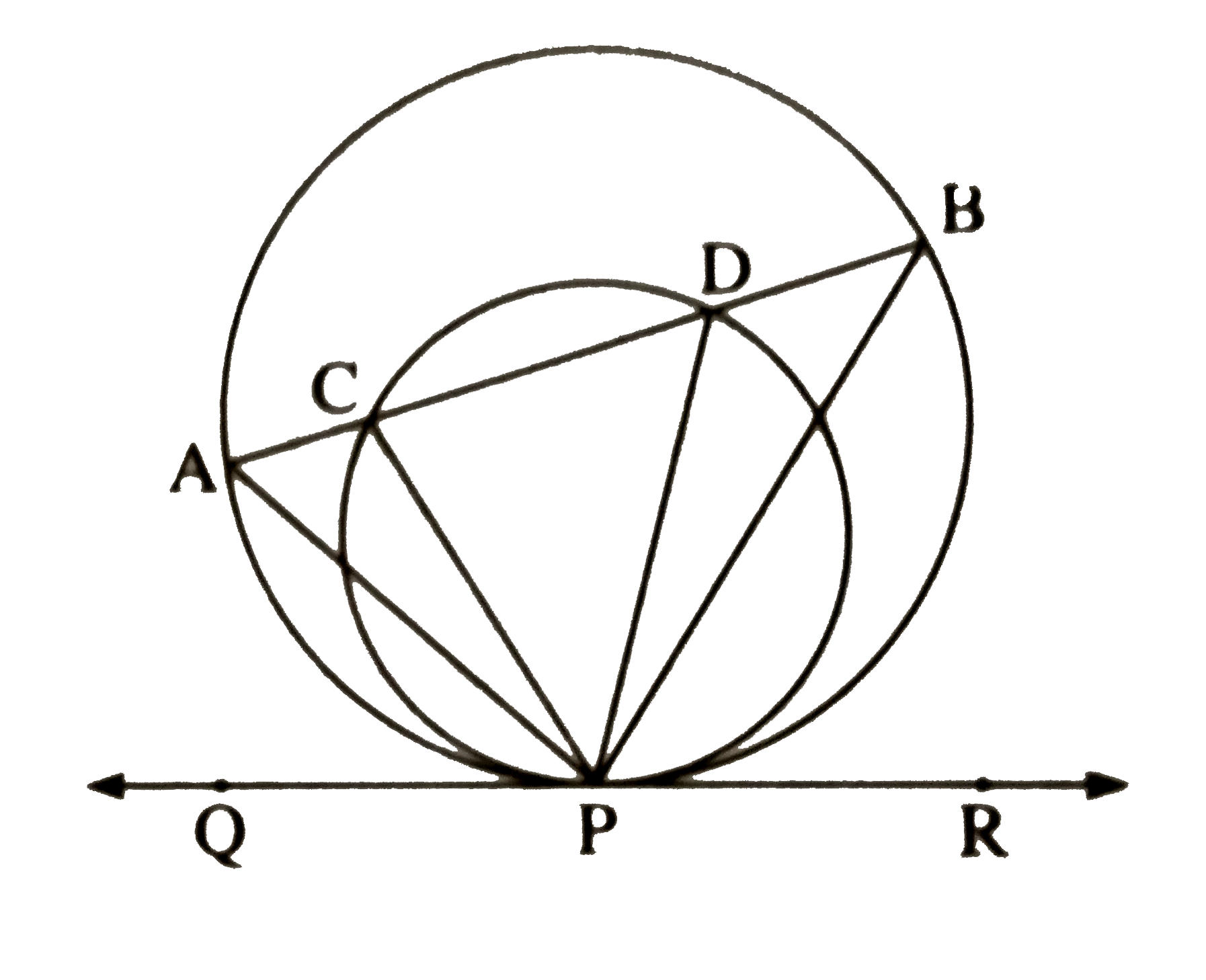
Two circles are tangent internally at P and a chord, AB of the larger circle is tangent to the smaller circle at C. PB and PA cut the smaller circle at E and D, respectively. If AB = 15 cm, While PE = 2 cm and PD = 3 cm. Find AC

Options

A. 6 cm
B. 8 cm
C. 3 cm
D. 9 cm

Explanation

To solve the problem, we need to find the length of segment AC in the given configuration of two internally tangent circles and a chord AB of the larger circle that is tangent to the smaller circle at point C.

1. Understand the Configuration:
- We have two circles: a larger circle and a smaller circle that is tangent internally at point P.
- A chord AB of the larger circle is tangent to the smaller circle at point C.
- The segments PB and PA intersect the smaller circle at points E and D, respectively.

2. Assign Known Values:
- Given:
- Length of chord AB = 15 cm
- Length of PE = 2 cm
- Length of PD = 3 cm

3. Set Up Variables:
- Let AC = x cm.
- Therefore, BC = AB - AC = 15 - x cm.

4. Use the Power of a Point Theorem:
- According to the theorem, for point P:
- \( PA \cdot PD = PC^2 \)
- \( PB \cdot PE = PC^2 \)

5. Calculate PA and PB:
- From the given values:
- \( PA = PD + AD = 3 + (x) \)
- \( PB = PE + BE = 2 + (15 - x) \)

6. Set Up the Equations:
- Using the power of point P:
- \( (3 + x)(x) = (2 + (15 - x))(15 - x) \)

7. Expand and Simplify:
- Expanding both sides:
- Left Side: \( 3x + x^2 \)
- Right Side: \( (2 + 15 - x)(15 - x) = (17 - x)(15 - x) \)
- Expanding the right side gives: \( 255 - 17x + x^2 \)

8. Set the Equation:
- Equating both sides:
- \( 3x + x^2 = 255 - 17x + x^2 \)

9. Cancel x² and Rearrange:
- Cancel \( x^2 \) from both sides:
- \( 3x = 255 - 17x \)
- Rearranging gives:
- \( 3x + 17x = 255 \)
- \( 20x = 255 \)

10. Solve for x:
- \( x = \frac{255}{20} = 12.75 \) cm

11. Find AC:
- Since we defined AC as x, we have:
- \( AC = 12.75 \) cm.

Final Answer:
- The length of AC is 12.75 cm.